二维离散Lorenz混沌系统的复杂度分析

冉 杰，刘衍民，王常春，王正伟

（遵义师范学院数学学院，贵州遵义563006）

1 引言

混沌伪随机序列的复杂性是指伪随机序列接近随机序列的程度。越接近随机序列，其复杂度越大，因此，伪随机序列复杂性是衡量保密通信系统抗干扰、抗截获能力的重要指标之一[1]。因此复杂度的分析具有重要的研究价值。

关于复杂度的分析已经有大量的学者研究。一些有关混沌时间序列复杂度研究的工作如下：文献[1]对Logistic映射、Gaussian映射和TD-ERCS系统的混沌时间序列进行了复杂度分析。孙克辉等计算了TD-ERCS离散混沌伪随机序列的复杂度大小[2]。文献[3]采用强度统计复杂度算法，分别对离散混沌系统(TD-ERCS)和连续混沌系统(简化Lorenz系统)进行复杂度分析。罗松江等以Logistic映射和耦合映像格子映射产生的混沌序列和多进制混沌伪随机序列为例，用增强统计复杂度方法，分析了混沌伪随机序列的复杂度[4]。更多复杂度的研究见文献[5-11]。

虽然关于复杂度的研究已经有大量的成果，但是这些成果远不能满足实际需求。复杂度的研究仍然是一个艰巨而深远的研究主题。关于复杂度的研究工作还需进一步的深入。基于此，本文借助谱熵算法，讨论二维离散Lorenz混沌系统的复杂度。

2 谱熵复杂度算法

谱熵(spectralentropy,SE)采用傅里叶变换，通过傅里叶变换域内能量分布，结合香农熵得出相应谱熵值，其算法流程如下[1]：

第2步：离散傅里叶变换，对序列作如下傅里叶变换：

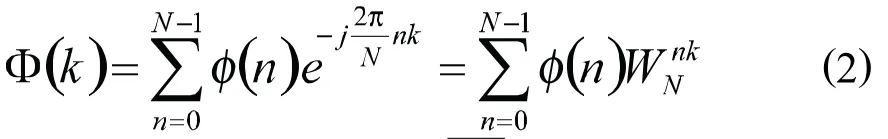
第4步：计算谱熵，利用Pk，得信号的谱熵（SE）为：

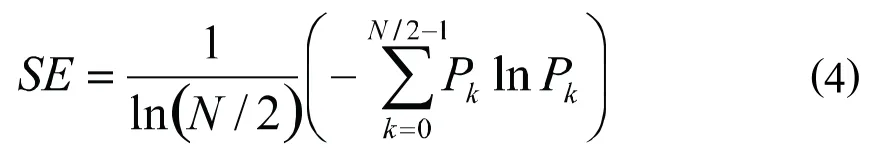
当序列功率谱分布越不均衡时，序列频谱结构越简单，信号中具有明显的振荡规律，得到的SE测度值越小，即复杂度越小，否则复杂度越大[1]。

3 二维离散Lorenz混沌系统的复杂度分析

利用上述的SE复杂度算法，计算二维离散Lorenz混沌系统的复杂度，并讨论参数的取值情况。

二维离散Lorenz混沌系统[8-10]如下：

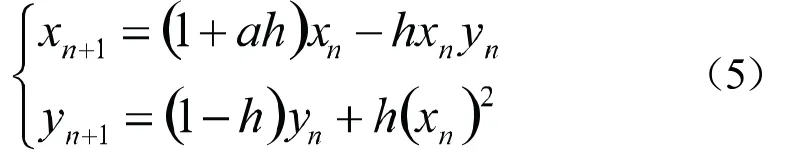
其中，a和h为系统参数。当a=0.85，h=1，系统（5）展现出混沌吸引子如图1。下面我们讨论系统（5）在 a∈［0，1］和h∈［0，1］之间的复杂度。计算结果如图2所示。基于图2，我们取a=0.95，h=1系统（5）展现出比图1更加复杂的混沌吸引子，如图3所示。

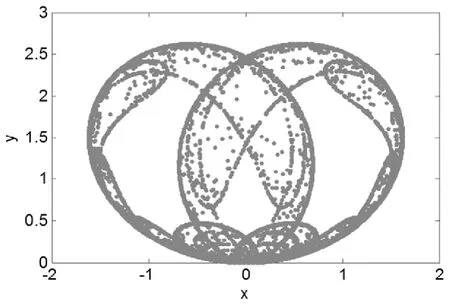
图 1 系统（5）的混沌吸引子，a=0.85，h=1。

图 2 系统（5）的 SE 复杂度，a∈［0，1］和 h∈［0，1］。

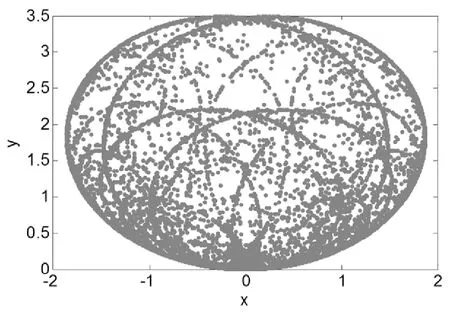
图 3 系统（5）的混沌吸引子，a=0.95，h=1。

4 结论

通过以上的分析，我们发现在图2的右上角区域具有较高的复杂度。进一步，当参数a∈［0.9，1］和h∈［0.9，1］时，系统的复杂度达到了0.9.也就是说当我们采用二维离散 Lorenz混沌系统作加密运算时，参数就可以选择在这个参数区间，让密匙更加复杂，难以破解。因此二维离散Lorenz混沌系统具有较好的应用前景。