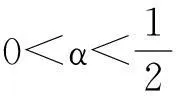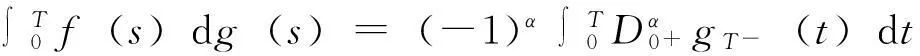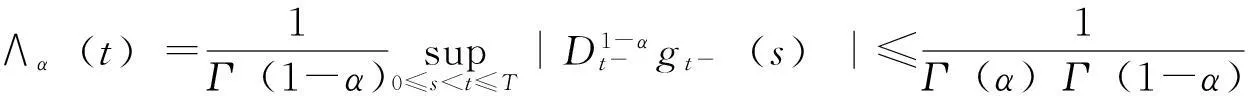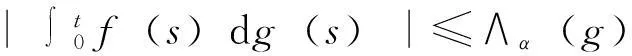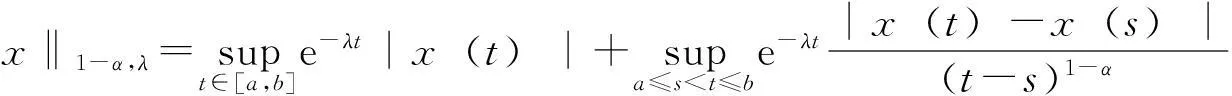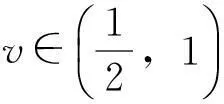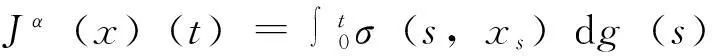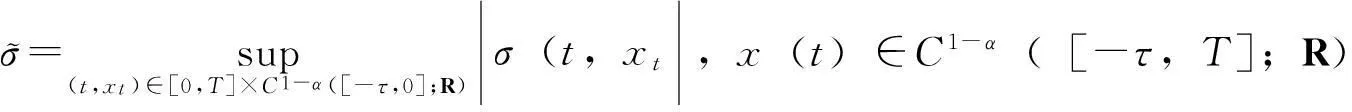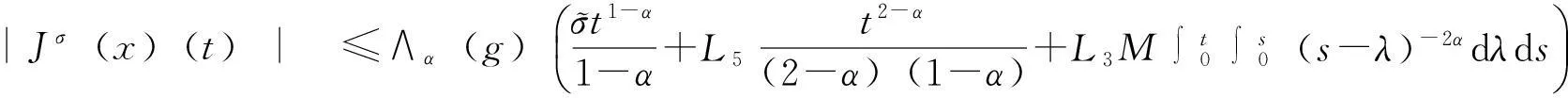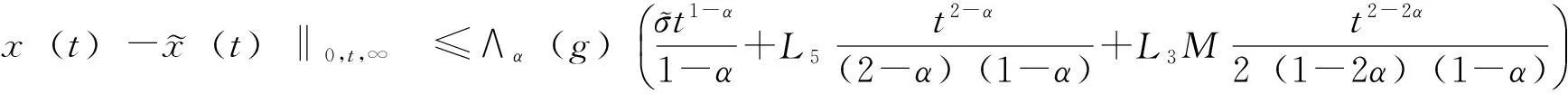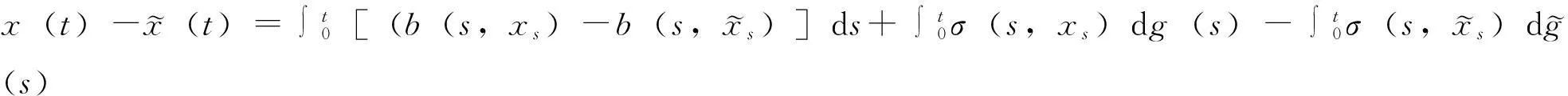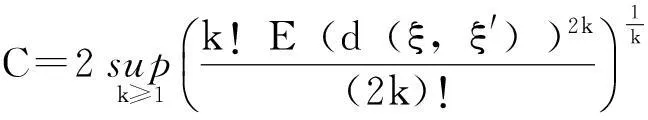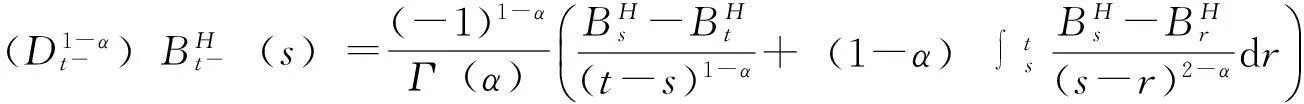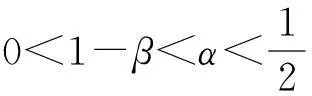由分数布朗运动驱动的随机泛函微分方程传输不等式

徐丽平，李治　(长江大学信息与数学学院，湖北 荆州 434023)



由分数布朗运动驱动的随机泛函微分方程传输不等式

徐丽平，李治(长江大学信息与数学学院，湖北 荆州 434023)

[摘要]通过分形分析方法，在Riemann-Stieltje积分意义下，对关于分数布朗运动的积分建立一些合理的估计，利用所建立的估计在赋予一致度量的连续函数空间上，对一类参数的分数布朗运动驱动的随机泛函微分方程解的概率分布建立Talagrand-类型T1传输不等式。

[关键词]传输不等式；Girsanov定理；分数布朗运动

假设(E,d)是赋予σ-域β的度量空间，且d是β⊗β-可测的。给定常数p≥1和E上的概率测度μ,ν，Wasserstein距离定义为：

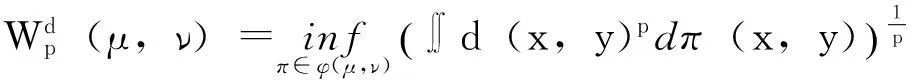
这里，φ(μ,ν)表示所有E×E上边缘分布为μ和ν的乘积概率测度。Talagrand[1]对Rn上的标准的Gaussian测度μ建立了传输不等式：

f>0μ(f)=0

其中，d(x,y)=|x-y|。

一般地，如果存在常数C≥0使得对任意的概率测度ν满足：

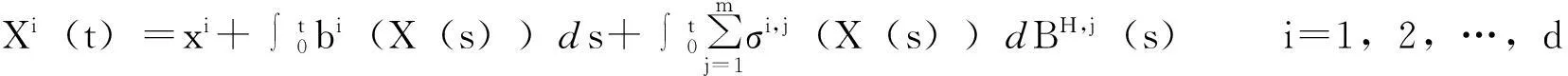
(1)

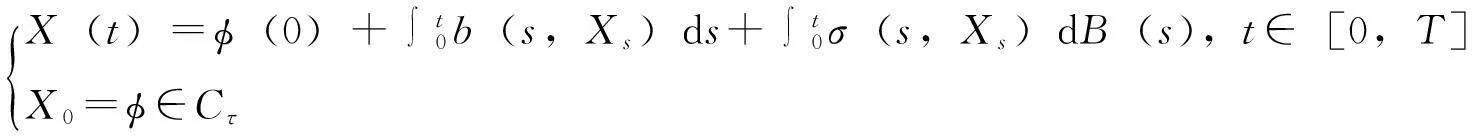
(2)

其中，Cτ=C([-τ,0];R)是[-τ,0]→R赋予一致范数‖·‖∞的连续函数空间；对∀u∈[-τ,0]，Xt∈Cτ表示函数Xt(u)=X(t+u)；b,σ:Ω×[0,T]×Cτ→R。

方程(2)中的随机积分是样本轨道意义下的Riemann-Stieltje积分。下面，笔者将应用一些最新的分数微分方程的结论和Girsanov变换方法，对方程(2)解的概率分布建立传输不等式。

1预备知识

对任意给定的T，考虑区间[0,T]，设(Wt)t∈[0,T]是定义在概率空间(Ω,F,P)上的布朗运动，记Ft=σ(Ws,s≤t)表示W生产的σ-代数。设BH=(BH(t))t∈[0,T]是定义在(Ω,F,P)由W变换得到的分数布朗运动，也就是说BH能表示为：

(3)

式中，核函数KH被定义为：

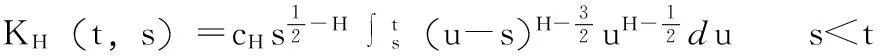
(4)

如果s≥t，则KH(t,s)=0。

对给定的实数0≤λ≤1及0≤s

‖f‖λ=‖f‖s,t,∞+‖f‖s,t,λ

其中：

考虑下面的假设条件：

(H1)函数b(t,ξ)是连续的，进一步，b(t,ξ)对t关于ξ是Lipschitz连续和线性增长的，即存在常数L1,L2使得对所有的ξη∈Cτ及t∈[0,T]满足：

|b(t,ξ)-b(t,η)|≤L1‖ξ-μ‖

|b(t,ξ)|≤L2(1+‖ξ‖)

(H2)函数σ(t,ξ)连续且对ξFrechet可微，进一步，存在常数L3,L4,L5使得对所有的ξ,η∈Cτ及t∈[0,T]满足：

|Dξσ(t,ξ)|≤L3

|Dξσ(t,ξ)-Dξσ(t,η)|≤L4‖ξ-η‖

|σ(t,ξ)-σ(s,ξ)|+|Dξσ(t,ξ)-Dξσ(s,ξ)|≤L5|t-s|

在假设条件(H1)、(H2)下，文献[9]证明了如果1-H<α

2由粗糙函数驱动的确定性微分方程

这里处理由Holder连续函数驱动的确定性微分方程，主要目的是证明由2个不同的Holder连续函数驱动的确定性微分方程的解关于一致度量d∞的估计。

(5)

的可测函数f:[0,T]→R和g:[0,T] →R，其中：

C1-α+ε([0,T];R)⊂W1-α+∞([0,T];R)⊂C1-α([0,T];R)∀ε>0

给定函数f∈Wα,1([0,T];R)及g∈W1-α,∞([0,T];R)，由分数阶导数算子[11]定义的一般化Stieltjes积分为：

定义：

进一步，有：

(6)

对任意的λ≥0，在空间C1-α([a,b];R)中引入下面的等价范数：

(7)

(8)

这里x0=φ∈Cτ。

‖x‖t-α,λ0≤M0

其中，λ0是依赖于T,α,Li的常数；M0是依赖于T,α,φ,Li的常数；i=1,…,5。

(9)

(10)

证明由式(6)，σ的有界性及假设条件(H2)知：

|Jσ(x)(t)|≤∧α(g)‖σ(xt)‖α,1

引理1得证。

进一步，如果令Δ=(2L1)-1∧1，则对所有的T≤Δ，存在常数K使得：

(11)

证明由方程(7)和(8)知：

利用式(6)及引理1有：

因此：

(12)

在式(12)中，令t=T并注意到对T≤1,有T1-α≥T2-2α≥T2-α，于是得到式(11)。

3主要结果

引理2[2]设μ是度量空间(E,d)上的概率测度，ξ,ξ′是概率分布为μ取值与E的2个独立的随机变量，如果：

有限，则μ在(E,d)上满足传输不等式T1(C)。

(13)

下面估计∧α(BH)。根据∧α的定义知：

因此：

另一方面，利用文献[7]中引理8知：

在式(13)两边取期望得：

因此，定理1得证。

注1在方程(2)中，如果τ=0，b,σ是时齐的，定理1弱化为文献[8]中的定理2，而文献[8]定理2的T1(C)性质中的常数C独立于初始值。但是对于泛函情况，在定理1中的C依赖于初值。尽管如此，对于仅仅漂移项含有时间延迟的情况下方程(2)的T1(C)性质中的常数C也独立于初始值φ。

(14)

可以得到定理2。

证明从定理1 的证明可知，如果命题1中的K独立于初始值函数φ，则定理2立即成立。为此，定义：

接下来估计Gσ(x)(t)。由式(6)，σ的有界性及假设条件(H2)知：

|Gσ(x)(t)|≤∧α(g)‖σ(t,x(t))‖α,1

考虑下面2个确定性微分方程：

(15)

(16)

这里x(0)=φ(0)。

类似于命题1的证明，定义Δ=(2L1)-1∧1，则对所有的T≤Δ，存在独立于初始函数φ的常数K使得：

证毕。

4结语

利用分形分析的方法，在R上对一类分数布朗运动驱动的随机泛函微分方程在一致度量空间上建立了T1传输不等式。进一步，将在无穷维空间中，利用Girsanov变化方法对分数布朗运动驱动的随机时滞偏微分方程和中立型方程建立T1和T2传输不等式。

[参考文献]

[1]Talagrand M.Transportation cost for Gaussian and other product measures[J].Geom Funct Anal, 1996,6:587～600.

[2] Djellout H, Guilin A, Wu L.Transportation cost-information inequalities for random dynamical systems and diffsions[J].Ann Probab, 2004,32: 2702～2732.

[3] Wu L, Zhang Z.Talagrand’sT2-transportation inequality w.r.t.a uniform metric for diffusions[J].Acta Math Appl Sin Engl Ser, 2004,20: 357～364.

[4] Wang F Y.Transportation cost inequalities on path spaces over Riemannian manifolds [J]. Illinois J Math, 2002,46: 1197～1206.

[5] Wang F Y.Probability distance inequalities on Riemannian manifolds and path spaces[J]. J Funct Anal, 2004,206: 167～190.

[6] Wu L.Transportation inequalities for stochastic differential equations of pure jumps[J]. Ann Inst Henri Poincare Probab Stat, 2010,46: 465～479.

[7] Ma Y.Transportation inequalities for stochastic differential equations with jumps[J]. Stochastic Process Appl, 2010,120: 2～21.

[8] Saussereau B.Transportation inequalities for stochastic differential equations driven by a fractional Brownian motion[J].Bernoulli, 2012,18(1) :1～23.

[9] Boufoussi B, Hajji S.Functional differential equations driven by fractional Brownian motion[J].Compt Math Appl, 2011,62:746～754.

[10] Samko S G, Kilbas A A, Marichev O I.Fractional Integrals and Derivatives[M]. Yvendon:Gordonand Breach Science Publishers,1993.

[11] Zahle M.Integration with respect to fractal functions and stochastic calculus[J].Probab Theory Related Fields, 1998,111: 333~374.

[12] Nualart D, Rascanu A.Differential equations driven by fractional Brownian motion[J]. Collect Math, 2002,53: 55~81.

[编辑]洪云飞

[文献标志码]A

[文章编号]1673-1409(2016)01-0070-07

[中图分类号]O211.63

[作者简介]徐丽平 (1980-)，女， 硕士， 讲师，现主要从事随机微分方程方面的教学与研究工作； E-mail: xlp211@126.com。

[基金项目]国家自然科学基金项目(11271093)； 湖北省教育厅青年人才项目(Q20141306)。

[收稿日期]2015-10-28

[引著格式]徐丽平，李治.由分数布朗运动驱动的随机泛函微分方程传输不等式[J].长江大学学报(自科版)，2016,13(1)：70～76.