Fullerene图的L(p，q)-标号问题

董晓媛，马登举

(1.南通师范高等专科学校数理系，江苏 南通 226000；

2.南通大学理学院，江苏 南通 226007)



Fullerene图的L(p，q)-标号问题

董晓媛1，马登举2

(1.南通师范高等专科学校数理系，江苏 南通 226000；

2.南通大学理学院，江苏 南通 226007)

[摘要]主要研究了一类Fullerene图Fspan的L(2，1)-标号问题及L(1，1)-标号问题，给出了Fspan的L(2，1)-标号数和L(1，1)-标号数的上界分别为7和6.该结果验证了Georges和Mauro猜想与Wegner猜想对于Fullerene图Fspan均成立.

[关键词]L(p，q)-标号，Fullerene图

1预备知识

Fullerene图是一类3-正则3-连通的平面图，且其在平面上的一个嵌入中每个面的边界是5-圈或6-圈.[1-4]

定义图Fm如下：它的顶点集为

边集为

由Fm的定义知，Fm是一类3-正则图，且有m+2个圈，分别为：

(1) 当i=0时，有一个含5个顶点的圈：

C0=u0，1u0，2u0，3u0，4u0，5；

(2) 当i=1，2，…，m时，有一个含10个顶点的圈：

Ci=ui，1ui，2…ui，10ui，1；

(3) 当i=m+1时，有一个含5个顶点的圈：

Cm+1=um+1，1um+1，2um+1，3um+1，4um+1，5.

按照m的奇偶性，Fm的一个平面嵌入如图1与图2所示.易见：Fm是一个3-连通的图，且每个圈的边界是5-圈或6-圈.因此Fm是一类Fullerene图.

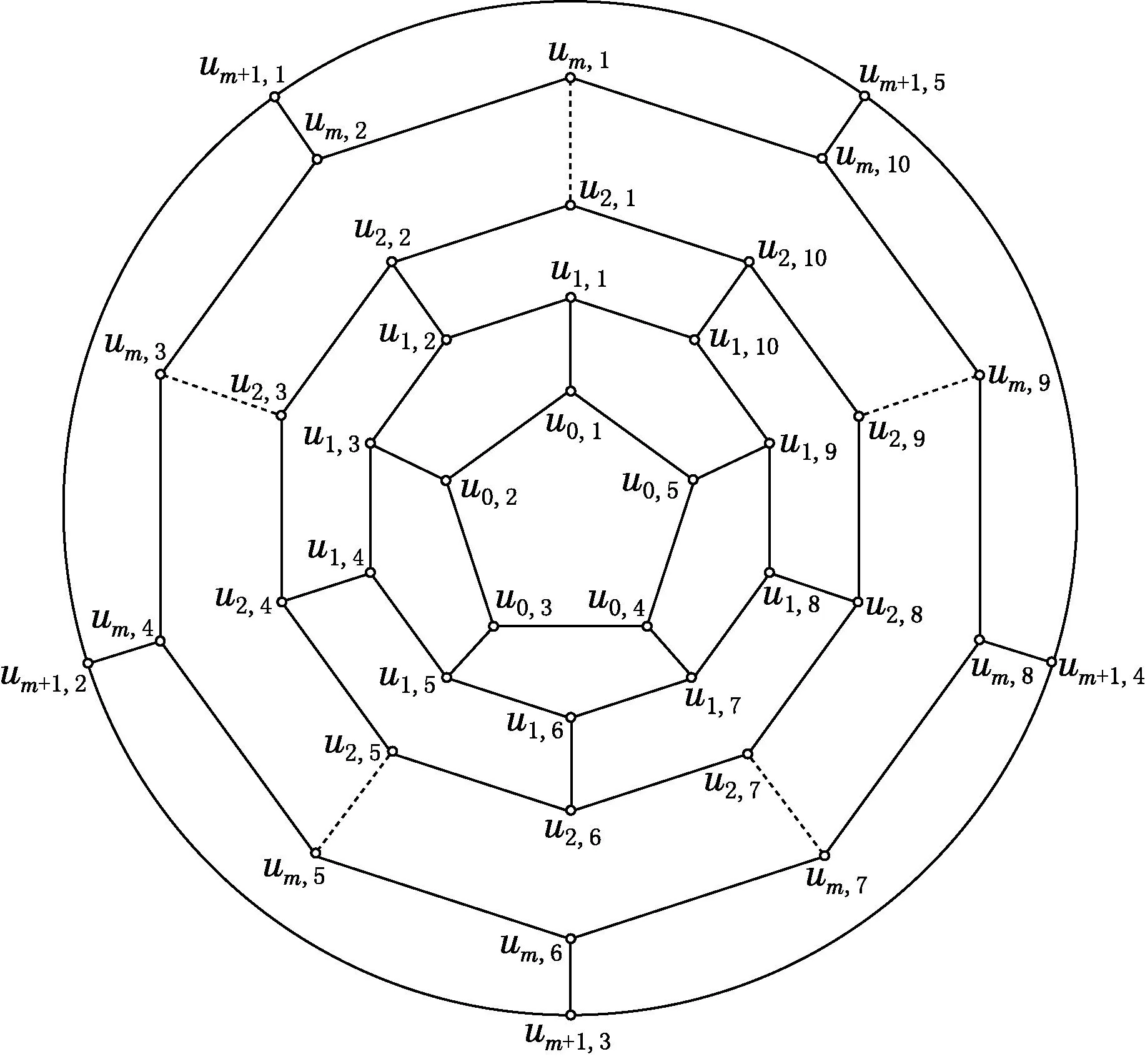
图1　当m为奇数时，Fullerene图Fm在平面上的一种嵌入

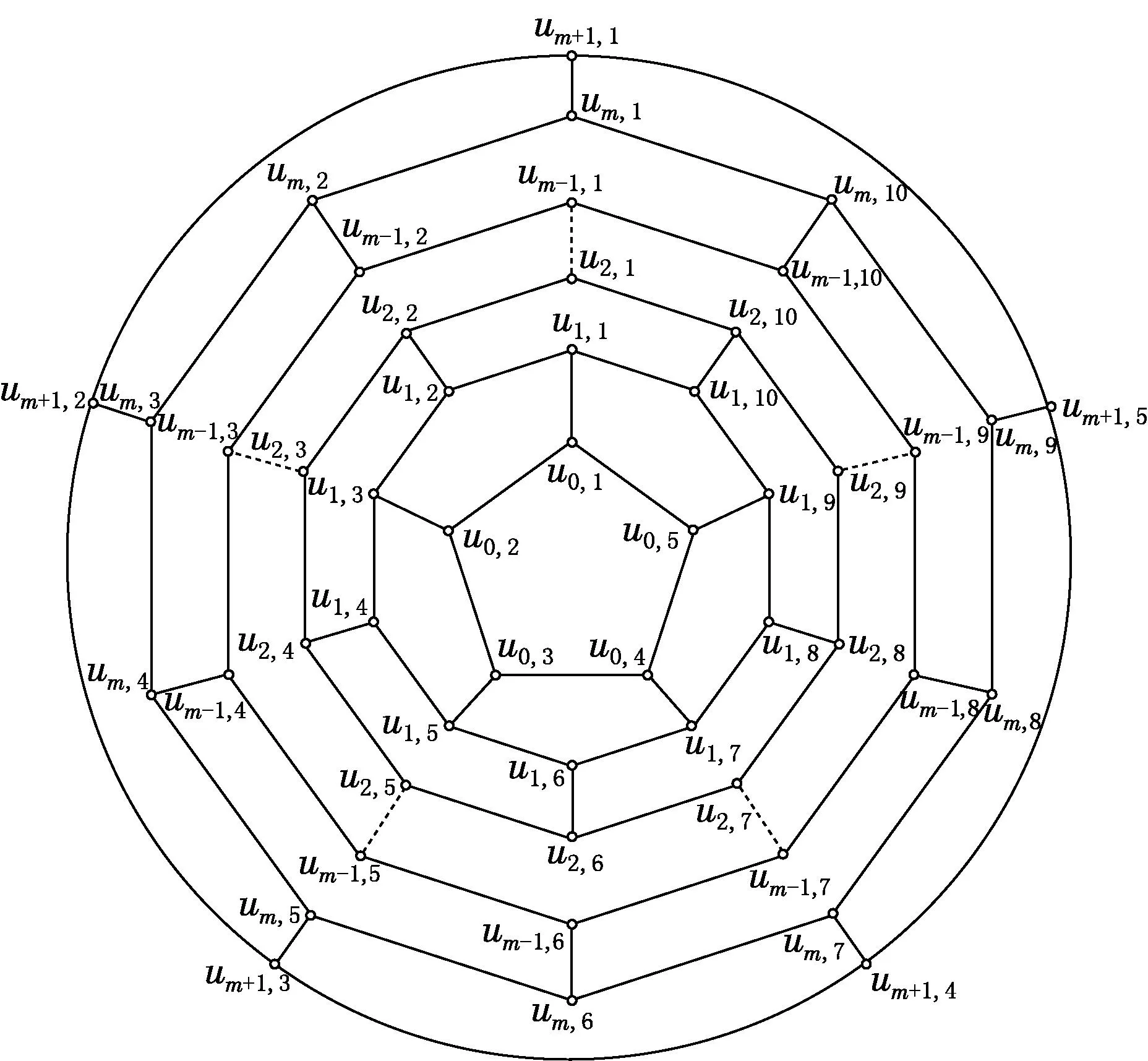
图2　当m为偶数时，Fullerene图Fm在平面上的一种嵌入

一个图G的L(p，q)-标号，是一个从G的顶点集V(G)到一个非负整数集的一个映射f，使得对G中的任意两个顶点u，v，当d(u,v)=1时，|f(u)-f(v)|≥p；当d(u,v)=2时，|f(u)-f(v)|≥q.这里d(u,v)表示u,v的距离.

一个图G的平方图G2是这样一个图，它的顶点集与G的顶点集相同，两个顶点相邻，当且仅当这两个顶点在G中的距离不大于2.

本文我们主要研究Fullerene图Fm的L(2，1)-标号问题与L(1，1)-标号问题.

2Fullerene图的L(2，1)-标号

定理1图Fm的L(2，1)-标号数λ2，1(Fm)≤7.

证明当m>10时，定义Fullerene图Fm的一个标号f如下：

f(u0，1)=7，f(u0，2)=1，f(u0，3)=6，f(u0，4)=3，f(u0，5)=0；

f(ui，1)=4，f(ui，2)=0，f(ui，3)=3，f(ui，4)=7，f(ui，5)=2，

f(ui，6)=5，f(ui，7)=7，f(ui，8)=4，f(ui，9)=6，f(ui，10)=1，i≡1(mod10)；

f(ui，1)=4，f(ui，2)=6，f(ui，3)=1，f(ui，4)=4，f(ui，5)=0，

f(ui，6)=3，f(ui，7)=7，f(ui，8)=2，f(ui，9)=5，f(ui，10)=7，i≡2(mod10)；

f(ui，1)=2，f(ui，2)=5，f(ui，3)=7，f(ui，4)=4，f(ui，5)=6，

f(ui，6)=1，f(ui，7)=4，f(ui，8)=0，f(ui，9)=3，f(ui，10)=7，i≡3(mod10)；

f(ui，1)=0，f(ui，2)=3，f(ui，3)=7，f(ui，4)=2，f(ui，5)=5，

f(ui，6)=7，f(ui，7)=4，f(ui，8)=6，f(ui，9)=1，f(ui，10)=4，i≡4(mod10)；

f(ui，1)=6，f(ui，2)=1，f(ui，3)=4，f(ui，4)=0，f(ui，5)=3，

f(ui，6)=7，f(ui，7)=2，f(ui，8)=5，f(ui，9)=7，f(ui，10)=4，i≡5(mod10)；

f(ui，1)=5，f(ui，2)=7，f(ui，3)=4，f(ui，4)=6，f(ui，5)=1，

f(ui，6)=4，f(ui，7)=0，f(ui，8)=3，f(ui，9)=7，f(ui，10)=2，i≡6(mod10)；

f(ui，1)=3，f(ui，2)=7，f(ui，3)=2，f(ui，4)=5，f(ui，5)=7，

f(ui，6)=4，f(ui，7)=6，f(ui，8)=1，f(ui，9)=4，f(ui，10)=0，i≡7(mod10)；

f(ui，1)=1，f(ui，2)=4，f(ui，3)=0，f(ui，4)=3，f(ui，5)=7，

f(ui，6)=2，f(ui，7)=5，f(ui，8)=7，f(ui，9)=4，f(ui，10)=6，i≡8(mod10)；

f(ui，1)=7，f(ui，2)=4，f(ui，3)=6，f(ui，4)=1，f(ui，5)=4，

f(ui，6)=0，f(ui，7)=3，f(ui，8)=7，f(ui，9)=2，f(ui，10)=5，i≡9(mod10)；

f(ui，1)=7，f(ui，2)=2，f(ui，3)=5，f(ui，4)=7，f(ui，5)=4，

f(ui，6)=6，f(ui，7)=1，f(ui，8)=4，f(ui，9)=0，f(ui，10)=3，i≡0(mod10).

对于Fullerene图Fm，当m>10时，从F1到F10的L(2，1)-标号以及定义可知：第0圈u0，1，u0，2，u1，3，…，u0，5总是依次标为7，1，6，3，0；第1圈u1，1，u1，2，u1，3，…，u1，9，u1，10依次标为4，0，3，7，2，5，7，4，6，1；第2圈u2，1，u2，2，u2，3，…，u2，9，u2，10依次标为4，6，1，4，0，3，7，2，5，7；照此类推，到第11圈的时候开始与第1圈重复标号，依次为4，0，3，7，2，5，7，4，6，1；第12圈与第2圈重复标号，依次为4，6，1，4，0，3，7，2，5，7；….也就是说，对于Fm，当m>10且m≡imod10，i=0，1，2，…，9时，Fm的第0圈与Fi的第0圈各顶点标号相同，Fm的第m圈与Fi的第i圈各顶点标号相同，Fm的第m+1圈与Fi的第i+1圈各顶点标号相同.而Fm的第1至m-1圈总是标4，0，3，7，2，5，7，4，6，1这10个数(顺序与F10相同).即Fm与Fi的L(2，1)-标号数相同.

这样，上面定义的Fullerene图的标号f是一个7-L(2，1)-标号.因此，Fullerene图的L(2，1)-标号数λ2，1(Fm)≤7.定理证毕.

1992年，Griggs和Yeh得到最大度为Δ的图G的L(2，1)-标号数的下界：

引理1[5]图G包含三个最大度Δ≥2的顶点，且其中一个顶点与另两个顶点相邻，则λ2，1(G)≥Δ+2.

由引理1可知λ2，1(Fm)≥5.

综上，Fm的L(2，1)-标号数5≤λ2，1(Fm)≤7.

2002年，Georges和Mauro[6]提出一个猜想：Petersen图是唯一一个L(2，1)-标号数为9的3-正则图，其他的3-正则图的L(2，1)-标号数总是至多为8.我们发现，对Fullerene图Fm这个猜想成立.

3Fullerene图的L(1，1)-标号

定理2Fm的L(1，1)-标号数λ1，1(Fm)≤6.

证明当m>10时，定义Fullerene图Fm的一个标号f如下：

f(u0，1)=1，f(u0，2)=0，f(u0，3)=3，f(u0，4)=2，f(u0，5)=5；

f(ui，1)=3，f(ui，2)=4，f(ui，3)=2，f(ui，4)=1，f(ui，5)=5，

f(ui，6)=0，f(ui，7)=4，f(ui，8)=3，f(ui，9)=0，f(ui，10)=6，i≡1(mod10)；

f(ui，1)=3，f(ui，2)=0，f(ui，3)=6，f(ui，4)=3，f(ui，5)=4，

f(ui，6)=2，f(ui，7)=1，f(ui，8)=5，f(ui，9)=0，f(ui，10)=4，i≡2(mod10)；

f(ui，1)=5，f(ui，2)=0，f(ui，3)=4，f(ui，4)=3，f(ui，5)=0，

f(ui，6)=6，f(ui，7)=3，f(ui，8)=4，f(ui，9)=2，f(ui，10)=1，i≡3(mod10)；

f(ui，1)=4，f(ui，2)=2，f(ui，3)=1，f(ui，4)=5，f(ui，5)=0，

f(ui，6)=4，f(ui，7)=3，f(ui，8)=0，f(ui，9)=6，f(ui，10)=3，i≡4(mod10)；

f(ui，1)=0，f(ui，2)=6，f(ui，3)=3，f(ui，4)=4，f(ui，5)=2，

f(ui，6)=1，f(ui，7)=5，f(ui，8)=0，f(ui，9)=4，f(ui，10)=3，i≡5(mod10)；

f(ui，1)=0，f(ui，2)=4，f(ui，3)=3，f(ui，4)=0，f(ui，5)=6，

f(ui，6)=3，f(ui，7)=4，f(ui，8)=2，f(ui，9)=1，f(ui，10)=5，i≡6(mod10)；

f(ui，1)=2，f(ui，2)=1，f(ui，3)=5，f(ui，4)=0，f(ui，5)=4，

f(ui，6)=3，f(ui，7)=0，f(ui，8)=6，f(ui，9)=3，f(ui，10)=4，i≡7(mod10)；

f(ui，1)=6，f(ui，2)=3，f(ui，3)=4，f(ui，4)=2，f(ui，5)=1，

f(ui，6)=5，f(ui，7)=0，f(ui，8)=4，f(ui，9)=3，f(ui，10)=0，i≡8(mod10)；

f(ui，1)=4，f(ui，2)=3，f(ui，3)=0，f(ui，4)=6，f(ui，5)=3，

f(ui，6)=4，f(ui，7)=2，f(ui，8)=1，f(ui，9)=5，f(ui，10)=0，i≡9(mod10)；

f(ui，1)=1，f(ui，2)=5，f(ui，3)=0，f(ui，4)=4，f(ui，5)=3，

f(ui，6)=0，f(ui，7)=6，f(ui，8)=3，f(ui，9)=4，f(ui，10)=2，i≡0(mod10).

对于Fullerene图Fm，当m>10时，从F1到F10的L(1，1)-标号以及定义可知：第0圈u0，1，u0，2，u1，3，…，u0，5总是依次标为1，0，3，2，5；第1圈u1，1，u1，2，u1，3，…，u1，9，u1，10依次标为3，4，2，1，5，0，4，3，0，6；第2圈u2，1，u2，2，u2，3，…，u2，9，u2，10依次标为3，0，6，3，4，2，1，5，0，4；依此类推，到第11圈的时候开始与第1圈重复标号，依次为3，4，2，1，5，0，4，3，0，6；第12圈与第2圈重复标号，依次为3，0，6，3，4，2，1，5，0，4；….也就是说，对于Fm，当m>10且m≡i(mod10)，i=0，1，2，…，9时，Fm的第0圈与Fi的第0圈各顶点标号相同，Fm的第m圈与Fi的第i圈各顶点标号相同，Fm的第m+1圈与Fi的第i+1圈各顶点标号相同.而Fm的第1至m-1圈总是标3，4，2，1，5，0，4，3，0，6这10个数(顺序与F10相同).即Fm与Fi的L(1，1)-标号数相同.

这样，上面定义的Fullerene图Fm的标号f是一个6-L(1，1)-标号.从而λ1，1(Fm)≤6.定理证毕.

由图的色数及图的L(p，q)-标号的定义，可知图G的平方图的色数χ(G2)与G的L(1，1)-标号数有关，从而我们得出如下结论：

推论1Fm的平方图的色数χ(Fm2)=λ1，1(Fm)+1≤7.

在1977年，Wegner[7]曾猜想一个最大度为3的平面图G的平方图G2的色数χ(G2)≤7.我们的结果表明，对Fullerene图Fm，该猜想成立.

[参考文献]

[1]DOSLIC T. On lower bounds of number of perfect matchings in Fullerene graphs [J]. Mathematical Chemistry，1998，24:359-364.

[2]KARDOS F，KRAL D，MISKUF J. Fullerene graphs have exponentially many perfect matchings [J]. Mathematical Chemistry，2009，46:443-477.

[3]BUHL M，HIRSCH A. Spherical aromaticity of Fullerene [J]. Chem Rev，2001，101：1153-1183.

[4]马海成，汪小玲. 点圈并图的匹配等价圈数[J].东北师大学报(自然科学版)，2006，38(4)：36-40.

[5]GRIGGS J R，YEH R.K. Labeling graphs with a condition at distance two [J]. SIAM J Discrete Mathematics，1992(5)：586-595.

[6]GEORGES J P，MAURO D W. On generalized Petersen graphs labeled with a condition at distance two[J]. SIAM J Discrete Mathematics，2002，259:311-318.

[7]WEGNER G. Graphs with given diameter and a coloring problem[R] Germany：University of Dortmund，1977.

(责任编辑：李亚军)

L(p，q)-labeling of the Fullerene graphs

DONG Xiao-yuan1，MA Deng-ju2

(1.Department of Mathematics and Physics，Nantong Normal College，Nantong 226000，China；2.School of Science，Nantong University，Nantong 226007，China)

Abstract:The L(2，1)-labeling and L(1，1)-labeling of the Fullerene graph Fspanare studied. It is proved that the L(2，1)-labeling number and the L(1，1)-labeling number of Fspanare at most 7 and 6 respectively，which verify the correction of the guesses presented by Georges and Wegner respectively.

Keywords:L(p，q)-labeling；Fullerene graph

[中图分类号]O 157.5[学科代码]110·7470

[文献标志码]A

[作者简介]董晓媛(1984—)，女，硕士，讲师，主要从事图的染色问题及其应用研究；通讯作者：马登举(1968—)，男，博士，副教授，主要从事图的染色问题及其应用研究.

[基金项目]国家自然科学基金资助项目(11171114).

[收稿日期]2014-06-12

[文章编号]1000-1832(2016)01-0014-04

[DOI]10.16163/j.cnki.22-1123/n.2016.01.004