资源约束下可打断项目组合选择模型研究

李星梅，魏涵静，乞建勋，郭晓玲

(1.华北电力大学经济与管理学院，北京 102206；2.北京北重汽轮电机有限责任公司，北京 100040；3.中国科学院大学工程管理与信息技术学院，北京 100049)

资源约束下可打断项目组合选择模型研究

李星梅1，魏涵静2，乞建勋1，郭晓玲3

(1.华北电力大学经济与管理学院，北京 102206；2.北京北重汽轮电机有限责任公司，北京 100040；3.中国科学院大学工程管理与信息技术学院，北京 100049)

首先，本文在已有可打断项目组合选择模型的基础上，引入了消耗性资源和可更新资源约束，构建了一个更符合实际的新模型；其次，为了达到模型简化的目的，本文给出了资金约束的现值表示，并给出了理论证明；最后，利用GAMS对模型进行了算例分析。数值实验结果表明：1)资源约束下的项目打断有时可以给企业带来积极效益，这有别于已有的研究；2)在考虑资源约束的情况下，资源消耗少且同时收益高的项目应优先执行；3)当资源的供给量较少时，资源约束是决定项目选择的关键因素。此外，通过企业实际的案例对数值实验结果进行了验证。

项目组合选择；资源约束；可打断；资金现值

1 引言

自1952年Harry Markowitz提出均值-方差投资组合模型[1]开始，组合选择问题便引起了人们的关注。项目组合选择是指在有限的资源限制下，决策者从一组有限的备选项目中选择一个项目组合，使该组合能够最大限度地实现组织的战略目标[2]，如使组织利润最大化等。该问题已被应用在各个领域，如研究与发展[3]、资金预算[4]、信息系统/技术[5]等。

项目的执行是需要花费时间的。根据规划周期的不同，学者们将项目组合的执行过程抽象成单阶段和多阶段两种类型。针对多阶段项目组合选择问题[6]，Servakh和Sukhikh[7]考虑了收益再投资问题，Stummer和Heidenberger[8]在分析项目间相关性的基础上比较了考虑相关性与不考虑相关性给组合收益带来的差异，Ghasemzadeh和Archer[9]建立了一个针对项目组合选择问题的决策支持系统，Medaglia等[10]在项目组合选择中引入了紧前关系，寿涌毅和宋淳江[11]在研发项目合作伙伴选择问题中考虑了风险及合作伙伴间的协作关系，李秉祥和吴建祥[12]在长短期项目选择的可分离均衡中考虑了经理人的管理防御行为，于超和樊治平[19]在多个行业的风险投资项目选择过程中考虑了决策者后悔规避因素等等。这些文章都认为一旦项目开始直到完成都不能被打断。然而，项目执行过程中一些不可预见的因素会导致项目被打断执行，如资金缺乏、原材料供给不足、技术工人缺失等。只有当资金补足、原材料到位、技术工人补足后，项目才能继续执行[13]。基于此，本文的着眼点落在可打断项目的组合选择问题的研究上。

基于现实的考虑，Li Xingmei等[14,20-21]假设项目的执行是“可打断”的，并综合考虑了项目的资金约束、收益再投资、紧前关系约束和生产准备成本等，继而构建了可打断项目组合选择模型。然而，文章中却忽略了资源约束对项目组合的影响。Ghasemzadeh和Archer[9]在项目选择问题中考虑了可更新资源约束的影响，Chen Jiaqiong等[15]在项目选择和调度问题中引入了资源约束，并认为资源是有限的而且可更新的，Liu Shushun等[16]提出了一种依赖于时间的资源约束，郭研和董超[17]在资源约束的前提下进行了高新技术企业研发项目选择策略研究等等。然而，项目一旦被打断，资源的分配就会发生变化。在项目可打断的情况下考虑资源约束，目前作者还没有看到相关研究。此外，资源也是制约着项目是否被打断的一个重要因素，因此在可打断情况下引入资源约束是很有必要的。

资源约束包括消耗性资源约束和可更新资源约束，消耗性资源是指在项目启动时以总量出现，并随着项目进展逐渐消耗的资源，例如各种原材料、能源等[18]。可更新资源是指在每个时刻的供应量都是有限的，在这一时间段内会消耗，但在下一时刻初会重新更新，例如人力、设备等。本文以项目可打断为基础来研究多阶段的受两种资源约束的项目组合选择问题。

基于上述分析，资源约束这一重要现实因素加入到可打断项目组合选择模型中去，构建出新的考虑资源约束的项目组合选择模型，并给出资金约束现值表示，在附录部分给出了理论解释，最后用GAMS对实际算例进行分析，数值结果表明资源约束下的项目可打断会给企业带来积极的影响。

2 模型建立

2.1 模型参数

假设可供选择的项目集合为V，j∈V，j=1,2,…,n，n表示可供选择项目的个数；A表示计划投资期的集合，t∈A，t=1,2,…,T,T代表计划投资期的期数,t时间段表示(t-1)时刻到t时刻之间的时间段间隔；K(t)表示在t时刻对所有项目的初始可投入资金,t=0,1，…，T-1；kj代表完成整个项目j需要的投资；r0表示折现率；cj表示项目j完成后的收益；sj表示项目j的生产准备成本；∑表示紧前关系的集合，即若(i,j)∈∑，则直到项目i结束后项目j才能开始；zj是一个布尔变量，如果在整个投资期内项目j被选择，则zj=1，反之zj=0；xjt表示在t时间段内项目j执行的比例且xjt∈0∪[αjt,βjt]，其中αjt表示在t时间段项目j执行比例的最小值，βjt表示在t时间段项目j执行比例的最大值；yjt是一个布尔变量，如果xjt=0则yjt=0，否则yjt=1；N表示整个投资期内可选择项目的最大数量；Mt表示在t时间段内可选择项目最大数量。

2.2 资源约束

消耗性资源和可更新资源约束将被分别描述如下：

2.3 资源约束下可打断项目组合选择模型构建

基于上述分析，在考虑消耗性资源和可更新资源约束的前提下，我们在Li Xingmei等[14]模型基础上构建了一个新的以收益净现值最大化为目标函数的项目组合选择模型，其(Model 1)表示如下：

其中，目标函数(1)是以收益净现值最大化为目标；约束(2)表示项目在每个时间段所执行的比例是受限制的，要介于最大值和最小值之间；约束(3)为紧前关系约束，即一个项目直到另一个项目完成后才能开始；约束(4)和(5)分别为消耗性资源约束和可更新资源约束；约束(6)和(7)分别是对整个投资期和每个时间段可执行项目数量的约束；约束(8)表示若一个项目被选择，则它必须在整个投资期内完工；原有的资金约束采用资金的将来值表示，约束(9)给出了资金约束采用资金的现值表示，具体的理论解释见附录；公式(10)-(12)表示变量取值范围的界定。

该模型为混合整数线性规划模型，其中有“nT+n”个0-1变量，“nT”个连续变量，约束的个数取决于集合∑中包含元素的个数。

2.4 资源约束下不可打断项目组合选择模型构建

如果项目在一个时间段内要么不执行(xjt=0)，要么就执行完(xjt=1)，这称为不可打断。基于此，在可打断项目组合选择模型基础上，得到了资源约束下不可打断项目组合选择模型，其(Model2)表示如下：

该模型为整数线性规划模型，其中有“nT+n”个0-1变量，约束的个数取决于集合∑中包含元素的个数。

2.5 两个模型比较分析

Model 1引入了介于αjt和βjt的连续变量xjt，即通过这个连续变量把“可打断”的思想引入到项目组合选择的模型中来；Model2中xjt的取值是0-1变量，它表示项目在一个时间段内，要么不选，要选就要执行完。若Model1中αjt和βjt都取特殊值，即αjt=0，βjt=1，Model2就是Model1的一个特殊情况，它的最优解也是Model1的可行解。

3 数值实验

由于可打断项目组合选择问题属于NP-hard问题，因此根据新模型的特点，本文采用GAMS软件求解。通过选取B公司的一些数据，应用GAMS软件对数据进行分析进而求出目标函数的最大值，以此来证明研究资源约束下可打断项目组合选择模型的必要性。

首先B公司整个投资期内可供选择项目的数量是20(n=20)；整个计划投资期分为10个时间段(T=10)；每个项目所需的投资和项目完成后的收益以及每个时刻的初始资金如表1和表2所示。

项目紧前关系的集合Σ={(1,5), (2,12), (3,5), (5,10), (8,11), (8,20)}，如(1,5)表示项目1完成后项目5才能开始；折现率r0为5%；每个项目的生产准备成本sj都为100万美元；整个投资期内可执行项目的最大数量N=12；每个时间段内可执行项目的最大数量Mt=2；表3代表每个项目对消耗性资源的需求量，我们将每种消耗性资源的总量固定为25，即Gm=25。

表1 每个项目所需投资和项目完成后的收益 单位：百万美元

表2 每个时刻的初始资金 单位：百万美元

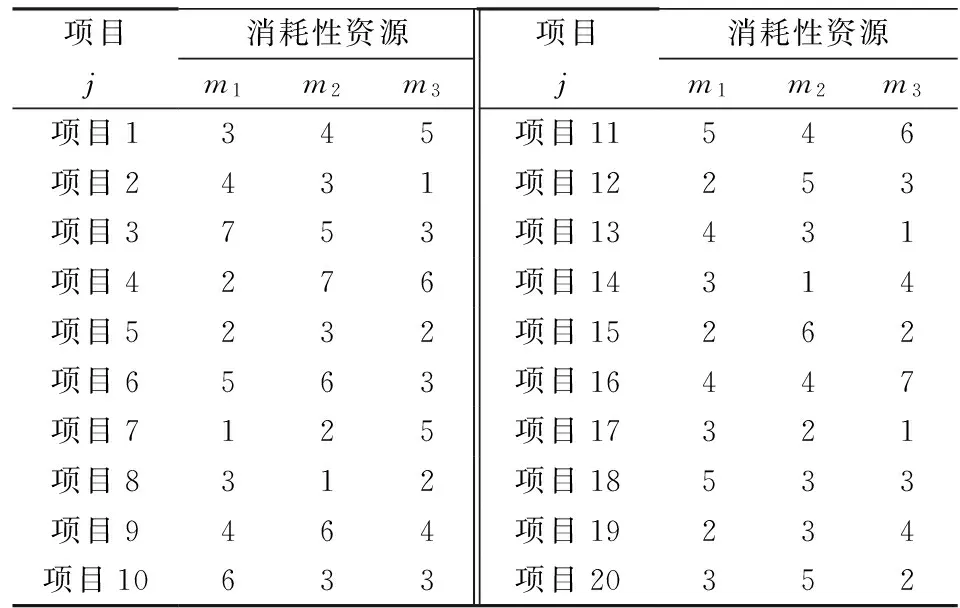
表3 每个项目对消耗性资源的需求量(由于资源是一种统称，故不设单位)

随后我们给出了可更新资源约束的数据。由于可更新资源在每个时刻初期都能重新更新，并且可能每个时间段的量是相同的。我们假设一种可更新资源在每个时间段可用的量是固定的。每个项目对可更新资源的需求量如表4所示，表5给出每个时刻可更新资源供给量。

表4 每个项目对可更新资源的需求量(由于资源是一种统称，故不设单位)

基于这些数据，我们得到了在资源约束下项目不可打断时执行的项目以及项目执行的时间，结果如表6所示。此时目标函数值为1.27亿美元，在整个投资期内执行的项目数量为4个，分别是1、2、4、16，从结果我们可以看出，由于资源的约束使得很多项目不被选择，同时当资源供给量少时，资源是决定项目组合的决定因素。以项目5为例，项目5的净收益在所有项目中是最大的，但是由于项目5对可更新资源p1的需求超过任何时间段内p1的供给量，从而导致项目5不被选择。而项目16尽管净收益很少，但是综合多个方面的因素，项目16在被选择行列中。

表5 每个时刻可更新资源的供给量

当考虑到项目可打断时，则规定了每个时间段内项目执行比例的最大值为0.5，最小值为0.2，即αjt=0.2，βjt=0.5。此时的结果如表7所示，其中18(0.29)表示在该时间段项目18执行，并且执行比例为29%，在项目可打断时，执行的项目为1、2、4、8、14、15、18，这时净现值为1.47亿美元。

由表6和表7对比可以看出，在资源约束的前提下，项目可打断与项目不可打断时相比，净现值由1.27亿增加到了1.47亿，增长了很多，执行的项目从1、2、4、6变为1、2、4、8、14、15、18，同时执行的项目数量由4个增加为7个。资源约束下项目可打断会影响选择的项目、项目的数量、项目的执行比例，进而影响项目组合的净现值。以上结果表明：考虑到资源约束则资源是影响着项目组合的关键因素，同时资源约束下考虑到项目可打断可以为企业带来更大的收益，从而证明了资源约束下可打断项目组合选择模型的必要性。

为进一步说明模型的实际可应用性，现以华电集团新能源技术公司项目决策为例。2015年该公司可供选择的总承包工程项目共20个，其中风电项目14个，光伏项目6个。经专家预测，各项目的收益与成本如表8所示，初始投入资金如表9所示，项目执行比例的最大值为0.7，最小值为0.3，项目的生产准备成本为0.1亿元。此时，其资源约束下可从表10可以看出，华电集团新能源技术公司选择执行风电项目1、2、3、5、7、10和光伏项目19时，收益最大，其净现值为11.55亿元。以上实际案例的应用，证明本文研究在项目决策中是具有实际意义的。

表6 资源约束下不可打断模型求解结果

打断模型求解结果如表10所示。

表7 资源约束下可打断模型求解结果

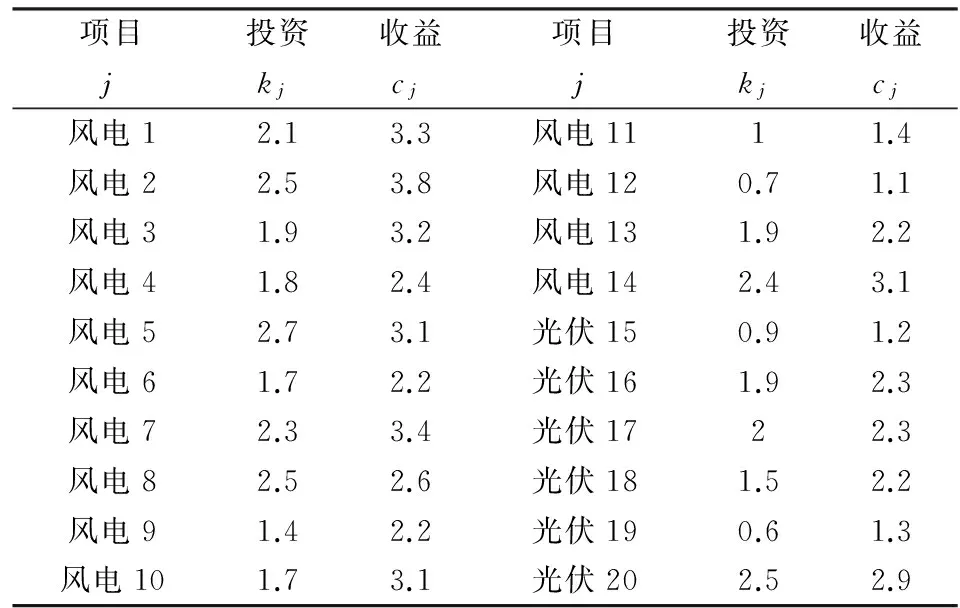
表8 每个项目所需投资和项目完成后的收益 单位：亿元

表9 每个时刻的初始资金 单位：亿元

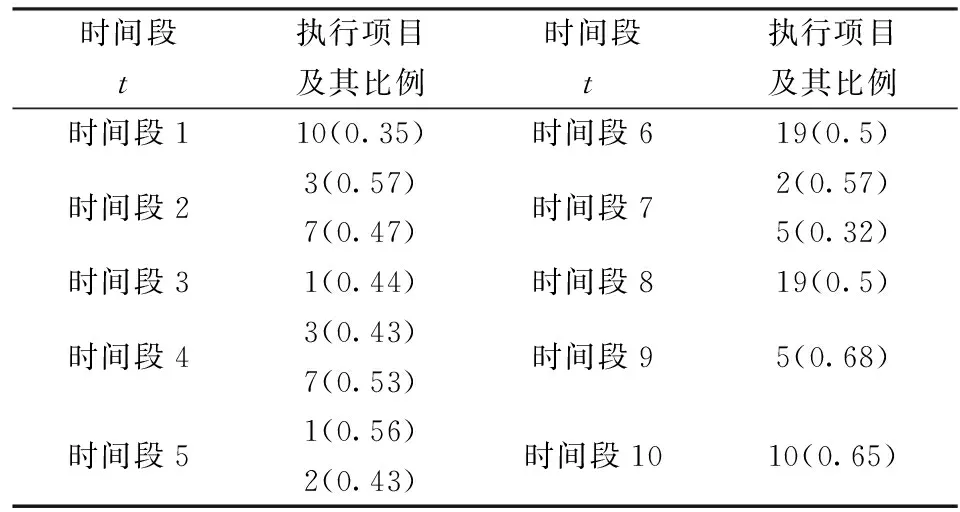
表10 资源约束下可打断模型求解结果

4 结语

文章在可打断项目组合选择模型中加入资源约束，并引入实际算例证明了加入资源约束对现有模型的影响，研究结果表明：当资源供给量较少时，资源约束是决定项目选择的关键约束；在资源约束的前提下，项目可打断会给企业带来更多的收益，从而说明在项目组合选择问题中对项目可打断以及资源约束的研究的必要性。

研究下一阶段将在原有的可打断项目组合选择模型的基础上考虑多目标，即不单单以收益最大化为目标，同时考虑成本最小，效用最大等目标，以期构建更加完善的、符合企业长期发展的项目组合选择模型。

附录

已知资金将来值表示为

(13)

现值=将来值×(1+r0)-t。

将(13)×(1+r0)-t得:

(14)

展开(14)得：

(15)

当τ=0时，该式=K(0)，

(16)

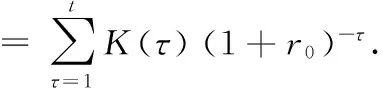
(17)

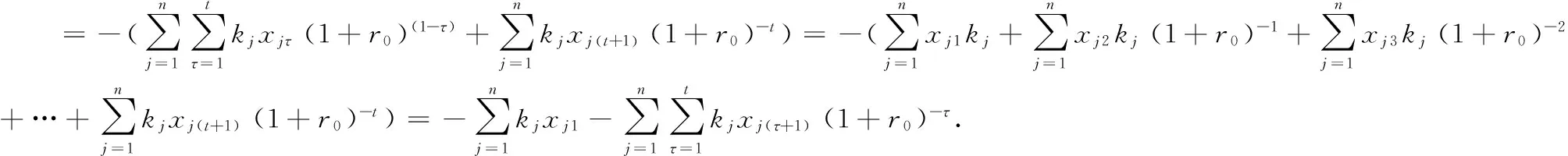
(18)

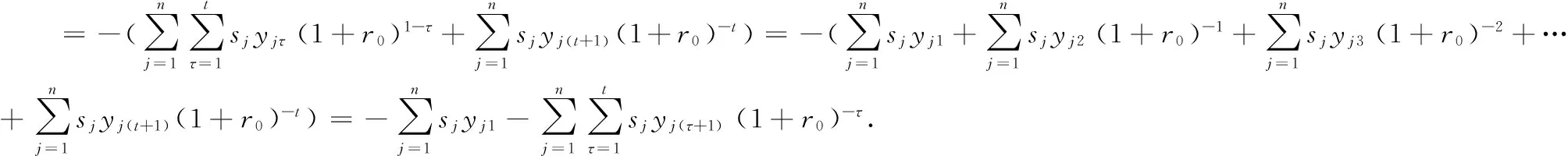
(19)

综合以上(16)-(19)式可以把(15)式整理为：

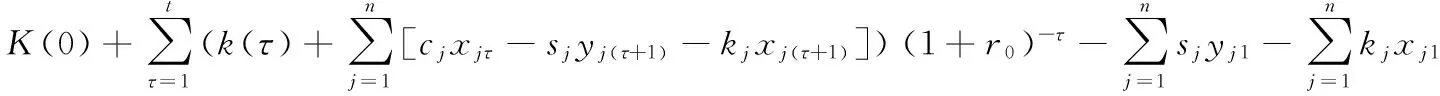
[1]MarkowitzH.Portfolioselection[J].TheJournalofFinance, 1952, 7(1): 77-91.

[2] 姚建伟. 资源受限项目组合选择及调度优化研究[D]. 杭州: 浙江大学, 2010.

[3]AbbassiM,AshrafiM,TashniziES.SelectingbalancedportfoliosofR&Dprojectswithinterdependencies:Across-entropybasedmethodology[J].Technovation, 2014, 34(1): 54-63.

[4]WeingartenHM.Capitalbudgetingofinterrelatedprojects:surveyandsynthesis[J].ManagementScience, 1966, 12(7): 485-516.

[5]ChoW,ShawMJ,KuonHD.Theeffectofsynergyenhancementoninformationtechnologyportfolioselection[J].InformationTechnologyandManagement, 2013, 14(2): 125-142.

[6] 谷晓燕. 基于实物期权的研发项目动态投资决策模型[J]. 中国管理科学, 2015, 23(7): 94-102.

[7]ServakhVV,SukhikhSL.Hybridalgorithmforschedulingwithregardforreinvestmentofprofits[J].AutomationandRemoteControl, 2004, 65(3): 449-455.

[8]StummerC,HeidenbergerK.InteractiveR&Dportfolioanalysiswithprojectinterdependenciesandtimeprofilesofmultipleobjectives[J].IEEETransactionsonEngineeringManagement, 2003, 50(2): 175-183.

[9]GhasemzadehF,ArcherNP.Projectportfolioselectionthroughdecisionsupport[J].DecisionSupportSystems, 2000, 29(1): 73-88.

[10]MedagliaAL,HuethD,MendietaJC,etal.Amulti-objectivemodelfortheselectionandtimingofpublicenterpriseprojects[J].Socio-EconomicPlanningSciences, 2008, 42(1): 31-45.

[11] 寿涌毅, 宋淳江. 复杂产品系统研发项目合作伙伴选择优化[J]. 科研管理, 2014, 35(10): 144-149.

[12] 李秉祥, 吴建祥. 管理防御视角下经理人长短期项目选择的可分离均衡[J]. 系统工程理论与实践, 2015, 35(4): 939-944.

[13]BelenkyAS.ABooleanprogrammingproblemofchoosinganoptimalportfolioofprojectsandoptimalschedulesforthembyreinvestingwithintheportfoliotheprofitfromprojectimplementation[J].AppliedMathematics, 2012, 25(10): 1279-1284.

[14]LiXingmei,FangSC,TianYe,etal.Expandedmodeloftheprojectportfolioselectionproblemwithdivisibility,timeprofilefactorsandcardinalityconstraints[J].JournaloftheOperationalResearchSociety, 2015, 66(7): 1132-1139.

[15]ChenJiaqiong,AskinRG.Projectselection,schedulingandresourceallocationwithtimedependentreturns[J].EuropeanJournalofOperationalResearch, 2009, 193(1): 23-34.

[16]LiuShushun,WangCJ.Optimizingprojectselectionandschedulingproblemswithtime-dependentresourceconstraints[J].AutomationinConstruction, 2011, 20(8): 1110-1119.

[17] 郭研, 董超. 基于资源约束的高新技术企业研发项目选择策略研究[J]. 项目管理技术, 2015, 13(4): 15-18.

[18] 方晨, 王凌. 资源约束项目调度研究综述[J]. 控制与决策, 2010, 25(5): 641-656.

[19] 于超, 樊治平. 考虑决策者后悔规避的风险投资项目选择方法[J]. 中国管理科学, 2016, 24(6): 29-37.

[20] 李星梅, 王雅娴, 刘再领, 等. 考虑风险因素的可打断项目组合选择问题[J]. 中国管理科学, 2015, 23(S1): 297-300.

[21] 李星梅, 刘再领, 赵秋红. 可打断项目组合选择问题局部敏感性分析[J]. 系统工程理论与实践, 2016, 36(7): 1816-1825.

Research on Project Portfolio Selection Model with Divisibility and Resource Constraints

LI Xing-mei1, WEI Han-jing2, QI Jian-xun1, GUO Xiao-ling3

(1.School of Economics and Management, North China Electric Power University, Beijing 102206, China;2.Beijing Beizhong Steam Turbine Generator Co., Ltd., Beijing 100040, China;3.College of Engineering & Information Technology, University of Chinese Academy of Sciences, Beijing 100049, China)

With the development of scientific technology and the acceleration of economic globalization, managers who own much capital face more and more projects to choose. How to invest the scarce resources such as budget, people and time. on a most profitable subset is crucial for a firm/organization. This is the main concern of project portfolio selection problem. In real world, managers note that project interruptions may happen, which come from some managerial concerns, such as the lack of cash, materials and technicians. When managers consider the project interruptions as a strategy in choosing the best execution scheduling for projects, i.e., in fact, they try to optimize the project execution by running the projects by portions, and the consideration of the project interruptions as the above strategy is manager’s initial intent. These types of interruptions are called divisibility. In this paper this type of project portfolio selection problem considering divisibility is mainly concerned. To the best of our knowledge, there is yet not research about resource constraints introduced into the project portfolio selection problem considering divisibility. Therefore, based on the model of project portfolio selection considering divisibility, a new model considering consumptive and renewable resource constraints is constructed. This model is a mixed integer programming problem with a linear objective function. And then a model of project portfolio selection problem without divisibility is set up. This model is an integer programming problem. The comparison analysis of the above two models is presented.More specifically, the second model is the special case of the first model under some assumptions. Secondly, for the purpose of simplifying the above models, the capital present value presentation is introcluced and proved. Finally, one numerical example is given to illustrate the characteristic of the new model with using GAMS. The result shows that: 1) unlike the research of the past, project divisibility can bring positive influence for the enterprise under the resource constraints. 2) Those projects with more profits and less use of resources are required precedence over all others. 3) When resources are limited, resource constraints are key factors for the selection of projects. A practical case provides the proof for the above results.

project portfolio selection; resource constraints; divisibility; capital present value

1003-207(2016)11-0040-07

10.16381/j.cnki.issn1003-207x.2016.11.005

2015-01-06；

2015-12-29

国家自然科学基金资助项目(71171079)；北京市产学研联合培养研究生共建项目资助

李星梅(1971-)，女(满族)，河北承德人，华北电力大学经济与管理学院，副教授，研究方向：项目管理、技术经济,E-mail:xingmeil@163.com.

F270.7

A