基于DEA-t检验的以企业为主体的科技创新效率评价

李鸿禧，迟国泰

(大连理工大学管理与经济学部，辽宁 大连 116024)

基于DEA-t检验的以企业为主体的科技创新效率评价

李鸿禧，迟国泰

(大连理工大学管理与经济学部，辽宁 大连 116024)

以企业为主体的科技创新效率评价是衡量科技投入后的产出水平、资源利用效率并寻找影响科技创新效率的主要因素，为优化资源投入结构打下基础。以企业作为科技投入和产出的主体，通过数据包络分析(DEA)中CCR模型和BCC模型测算中国15个副省级城市科技创新的总体投入产出效率、纯技术效率和规模效率。通过DEA-t检验的方法萃取出显著影响效率的关键指标，找到不同副省级城市各自效率偏低的关键问题。创新与特色一是将保留所有指标的DEA效率测算模型作为基础模型，将逐一剔除单个指标后的DEA效率测算模型作为对比模型。通过t检验，依次检验基础模型与每个对比模型的总体投入效率TE是否存在显著差异。若差异显著，则对比模型中剔除的指标为显著影响效率的关键指标，由此确定了影响科技创新效率的五个关键指标。改变现有研究的数据包络分析(DEA)方法仅仅能测算效率、无法萃取影响效率的关键因素的弊端。二是实证结果表明：显著影响以企业为主体的科技创新效率的关键指标为规模以上工业企业R&D经费内部支出、财政科技经费投入、科技从业人员数、技术市场成交额、规模以上工业企业新产品产值。三是实证结果表明：不同副省级城市导致效率偏低的关键问题大相径庭。如杭州的关键问题是“财政科技经费投入”的冗余率过大，而哈尔滨的关键问题是“规模以上工业企业新产品产值”的产出不足超高。

科技创新；科技效率；数据包络分析；t检验；关键因素

1 引言

以企业为主体的科技创新效率评价是以企业作为科技创新投入和成果转化主体[1]，衡量地区的科技投入产出水平，反映企业对整个地区科技创新效率的推动作用。

2014年全国政协一号提案为“关于发挥市场配置科技资源的决定性作用”，强调科技应以绩效为导向，推进应用型研究机构的市场化、企业化[2]。并且，十八届三中全会明确提出“要强化企业在技术创新中的主体地位”[1]，可见以企业为主体的科技创新已成为改革的关键。科技创新只有以企业为主体，才能坚持市场导向，反映市场需求。而科研机构单纯注重技术先进性，缺乏对市场的把握，其成果并不具有产业化的能力。

(1)基于非参数法的科技创新效率评价现状

杜娟等[3]利用数据包络分析(DEA)，从共享投入和分阶段产出两个阶段，测量中国重点城市的创新能力。晏蒙等[4]运用DEA方法对我国各省市工业的科技创新相对效率进行横向和纵向对比。李洪伟等[5]运用DEA三阶段模型对高技术产效率进行实证。范斐等[6]利用比较优势(NRCA)模型，对比各区域的科技资源配置效率。Sueyoshi T等[7]通过数据包络分析-判别分析，研究日本信息技术产业的研究效率。Odeck J等[8]综合利用数据包络分析与随机前沿生产函数，测度海港城市的科技效率。Lafarga C V等[9]利用数据包络分析对墨西哥的区域创新系统效率进行测度。

(2)基于回归参数法的科技创新效率评价现状

蒋仁爱等[10]采用FE和IVE方法控制双向偏误的基础上，估计了研究所投入要素对科技收入的贡献份额。戚湧等[11]基于SFA方法对全国和江苏科技资源市场配置效率进行评价。肖文等[12]采用随机前沿分析方法，测算了36个工业行业的技术创新效率。Xie Xin等[13]利用随机前沿分析方法，对科技创新效率和非效率因素进行了测算。Afzal M N I等[14]利用DEA和Tobit回归模型，对20个国家的创新效率进行评价，并找出效率低下的原因。Hu J L等[15]通过距离函数方法，对比分析24个国家的科技研发效率。

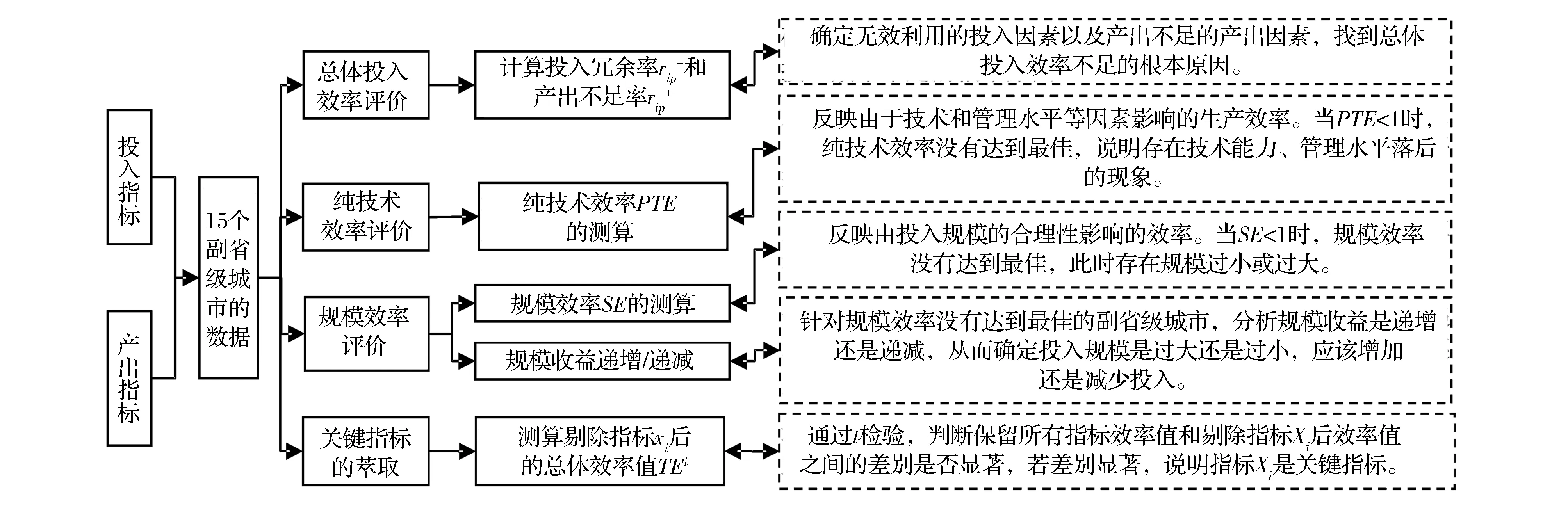
图1 以企业为主体的科技创新效率评价原理

上述现有研究存在的不足之处在于：

一是现有研究利用数据包络分析模型(DEA)模型仅能进行效率评价，无法找到显著影响效率的关键指标。二是现有研究在评价科技创新效率时、忽略企业的创新主体地位。

2 问题的难点及解决思路

2.1 问题的难点

难点一：如何针对不同的副省级城市找到各自效率无效的具体原因。

难点二：规模过大或过小都会导致效率不高，如何找到与投入规模对应的提高效率的方式。

难点三：如何萃取出能够显著影响以企业为主体的科技创新效率的关键指标。只有对关键因素加大力度，才能快速有效地提高效率。

2.2 突破难点的思路

难点一的解决思路：通过数据包络分析(DEA)中的CCR模型，求解总体投入效率TE并测算投入冗余率和产出不足率，确定副省级城市各自的投入无效因素以及产出不足因素。

难点二的解决思路：通过数据包络分析(DEA)中的BCC模型，测算规模效率SE，判断投入规模是过大还是过小，应该减少还是增加投入。

难点三的解决思路：将保留所有指标的DEA模型作为基础模型，将逐一剔除单个指标后的DEA模型模型作为对比模型。通过t检验，依次检验基础模型与每个对比模型的效率TE是否存在显著差异。若差异显著，说明对比模型中剔除的这个指标对总体投入效率具有显著的影响、即为关键指标。反之，则不是关键指标。

基于DEA-t检验的以企业为主体的科技创新效率评价原理如图1所示。

3 以企业为主体的科技创新效率评价原理及方法

3.1 投入和产出指标的选取

借鉴欧洲创新报告、中国科技技术评价、中国区域创新能力报告等国内外权威机构的经典指标[16-18]，结合文献的梳理[3-15]，选取“规模以上工业企业R&D经费内部支出X1”、“财政科技经费投入X2”、“科技从业人员数X3”为投入指标；“高新技术产业产值Y1”、“技术市场成交额Y2”、“规模以上工业企业新产品产值Y3”为产出指标。

通过效率评价的投入和产出指标，体现以企业为主体的科技创新：

①“规模以上工业企业R&D经费内部支出”、“科技从业人员数”直接反映企业的科技经费和人力投入；“高新技术产业产值”、“规模以上工业企业新产品产值”直接反映企业的科技产出和新产品的转化能力。

②“财政科技经费投入”间接反映政府对企业科技经费的投入。2012年全国科技经费支出为10298.4亿元，其中企业占76.2%[19]，说明全国科技经费支出中企业占绝大部分。

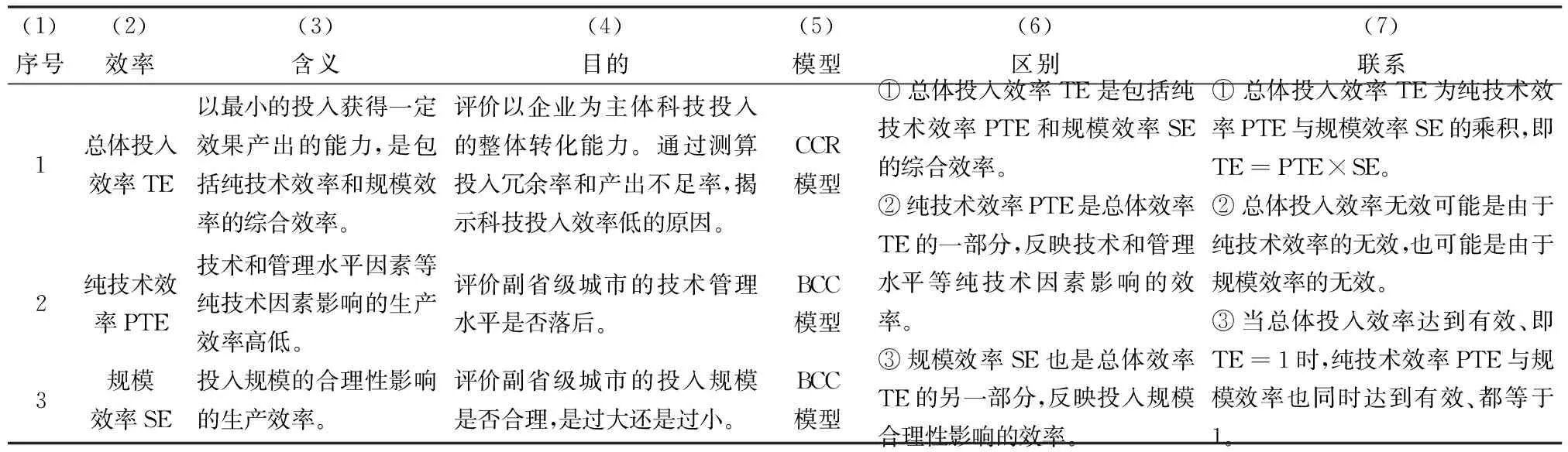
表1 三种效率的概述及对比

③“技术市场成交额”间接反映企业的技术交易额。2012年企业输出和吸纳技术合同成交额分别占全国技术合同成交总额86.54%和78.35%[20]，说明“技术市场成交额”绝大部分是企业的技术交易额。

3.2 所用的三种效率概述

本研究共涉及三种效率，分别是总体投入效率TE、纯技术效率PTE、规模效率SE。表1是三种效率的概述及对比。

3.3 总体投入效率评价

3.3.1 总体投入效率评价步骤

①测算总体投入效率TE。通过数据包络分析(DEA)中的CCR模型，测算总体投入效率TE，反映以企业为主体的科技投入整体转化能力的高低。当TE=1，实现总体投入有效，此时投入能够有效转化为成果产出。当TE<1，未实现总体投入有效，此时存在投入冗余或产出不足。

②测算投入冗余率。针对未实现总体投入有效(TE<1)的城市，计算投入冗余量si-和投入冗余率ri-，确定无效的投入、即未能有效利用的投入比例。

③测算产出不足率。针对未实现总体投入有效(TE<1)的城市，计算产出不足量si+和产出不足率ri+，确定没有全部成功转化为成果产出的比例。

3.3.2 总体投入效率TE的测算

设：θp-系数，TEp-第p个城市的总体投入效率，n-副省级城市的个数，xij-第j个城市第i种投入的投入量，λj-第j个城市对应的系数，sip--第p个城市第i种投入的冗余量，m-投入指标个数，yri-第j个城市第r种产出的产出量，srp+-第p个城市第r种产出不足量，s-产出指标的个数，则[21]：

minθp=TEp

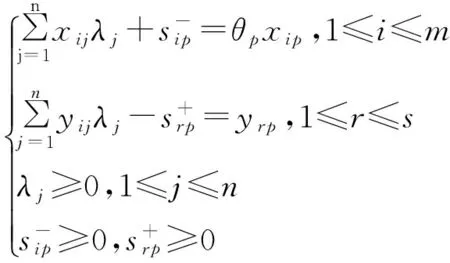
(1)

式(1)的含义：若TEp=1，则第p个城市实现了总体投入有效，此时sip-=0，sip+=0。若TEip<1，则未达到总体投入有效、sip->0或sip+>0，说明此时存在投入冗余或产出不足。

3.3.3 投入冗余率和产出不足率的测算

针对总体投入效率TEp<1的副省级城市，计算投入冗余率和产出不足率。

投入冗余率rip-等于投入冗余sip-除以实际投入xip。其中，投入冗余sip-的值可由式(1)求出。

rip-=sip-/xip

(2)

产出不足率rip+等于产出不足sip+除以实际产出yip。其中，产出不足sip+的值可由式(1)求出。

rip+=sip+/yip

(3)

3.4 纯技术效率评价

总体投入效率TE是包括纯技术效率PTE和规模效率SE的综合效率、即TE=PTE×SE。总体投入效率无效可能是由于纯技术效率的无效，也可能是由于规模效率的无效。所以，针对总体投入效率无效的副省级城市，3.4和3.5节分别从纯技术效率和规模效率两个方面进行进一步评价。

设：PTEp-第p个城市纯技术效率，SEp-第p个城市的规模效率。其余字符含义同式(1)，则[21]：

minθp=PTEp

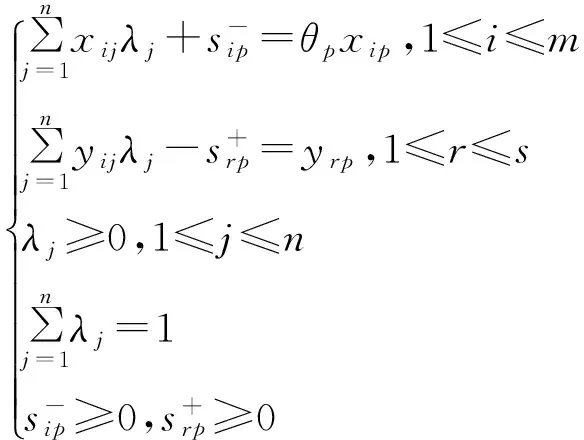
(4)

式(4)的含义：当PTEp=1，则实现了纯技术效率有效，技术水平和管理能力达到最佳。当PTEp<1，则未达到纯技术效率有效，说明此时的技术水平和管理能力落后。

3.5 规模效率评价

3.5.1 纯技术效率PTE和规模效率SE的测算

由于总体投入效率TE等于纯技术效率PTE与规模效率SE的乘积、即TE=PTE×SE，则规模效率SE的测算公式为[21]：

SEp=TEp/PTEp

(5)

其中，总体投入效率TEp可由式(1)测算，纯技术效率PTEp可由式(4)测算。

式(5)的含义：若规模效率SEp=1，现有的投入规模已达到最佳规模；若规模效率SE<1，现有的投入规模不合理，此时规模过小或过大，应该增大或减少科技投入。

3.5.2 规模收益递增/递减的判定

规模收益递增/递减的判定目的是确定投入规模是过大还是过小。

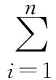
(6)

式(6)的含义：若规模收益系数Kp=1，此时规模效率达到了最佳值；若规模收益系数Kp<1，此时规模收益是递增的，说明此时的投入规模是过小的；若规模收益系数Kp>1，此时规模收益是递减的，说明此时的投入规模是过大的。

3.6 关键指标的萃取

3.6.1 关键指标萃取的目的

关键指标萃取的目的是确定哪些投入产出指标能够显著地影响企业为主体的科技创新效率。从而通过加大关键产出因素、合理调整关键投入因素，达到快速有效地提高效率的目的，改变了现有研究利用数据包络分析(DEA)模型仅能测算效率、不能萃取出关键因素的弊端。

影响效率的关键指标萃取原理如图2所示。

3.6.2 关键指标萃取的步骤

步骤1：将保留所有指标的效率测算模型作为基础模型，将在基础模型的基础上逐一剔除单个指标后的效率测算模型作为对比模型。关键指标萃取的基础模型与对比模型如表2所示。

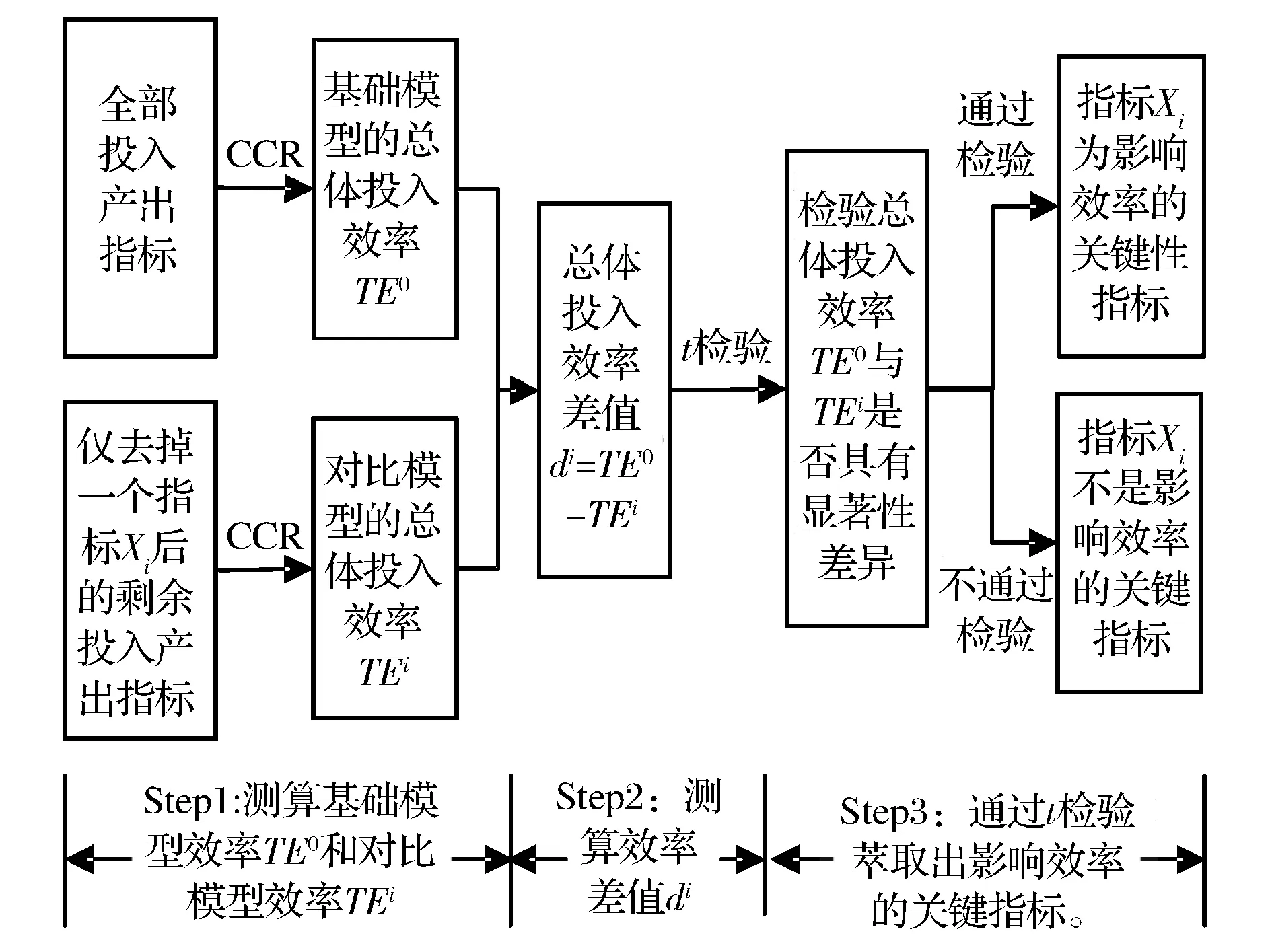
图2 影响效率的关键指标萃取原理

步骤2：分别测算出基础模型与每个对比模型的总体投入效率TE0和TEi，进而计算基础模型与每个对比模型的总体投入效率差值di=TE0-TEi。

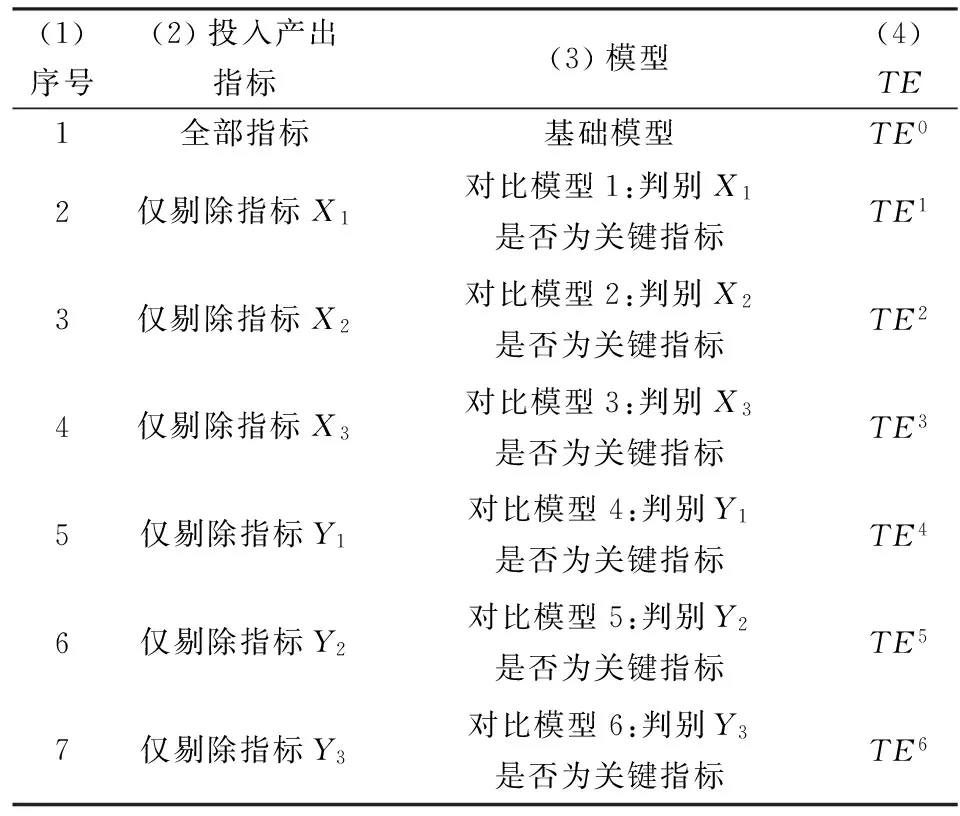
表2 基础模型和对比模型

步骤3：利用总体投入效率的差值di，构造t统计量，检验该差值是否显著。若差值di显著不为0，说明剔除指标Xi(或Yi)后的对比模型与基础模型测算出的效率值具有显著的差异，则该剔除指标Xi(或Yi)对总体投入效率具有显著的影响、即为关键指标。反之，则不是关键指标。

3.6.3 关键指标萃取的方法

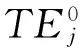
(7)

(8)

(9)

式(9)的含义：通过构造t统计量，检验第i个对比模型与基础模型测算的效率差值是否显著。其中，ti服从t(n-1)分布。

关键指标的判别标准：在5%的显著性水平[22]下、即置信水平为1-5%=95%时，若ti>t0.05(n-1)，则通过t检验，表示第i个对比模型的效率差值显著不为0、即剔除指标Xi(或Yi)后测算的效率值与全部指标测算的效率值具有显著的差别，则指标Xi(或Yi)对科技创新效率具有显著的影响、即为关键指标。反之，则不是关键指标。

4 以企业为主体的科技创新效率评价实证

4.1 样本的选取及数据来源

本研究选取长春、深圳、西安等15个副省级城市的2012年科技指标数据为实证样本。数据均来源于中国经济与社会发展统计数据库、各副省级城市的统计年鉴以及城市统计年鉴。投入产出指标的原始数据列于表3前15行第3-8列。

根据DEA模型的应用要求：决策单元数(样本的数量)要大于等于投入指标与产出指标总数的2倍[21]。本研究的样本数量为15，投入指标数量为3，产出指标数量为3，计算可知15>2×(3+3)，则本研究的样本数量满足DEA模型的要求。

4.2 总体投入效率评价

4.2.1 总体投入效率的测算及分析

在表3前15行中：将第3-5列的数据作投入指标，第6-8列的数据作为产出指标代入式(1)，求得15个副省级城市的总体投入效率TE，如表3第9列和图3所示。15个副省级城市的效率TE平均值列于表3第9列第16行。

由表3第9列和图3的总体投入效率TE可知：

①15个副省级城市的以企业为主体的科技创新效率平均值为0.87，整体效率水平较高。

②武汉、深圳、南京、哈尔滨、杭州、广州、济南、成都没有实现投入有效。而长春、大连、宁波、青岛、沈阳、西安、厦门实现投入有效。

③深圳、杭州、南京、广州的“高新技术产业产值”等产出指标的数值较高，但总体投入效率TE均小于1，说明深圳、杭州、南京、广州的产出水平较高、但没有实现科技投入的有效利用。

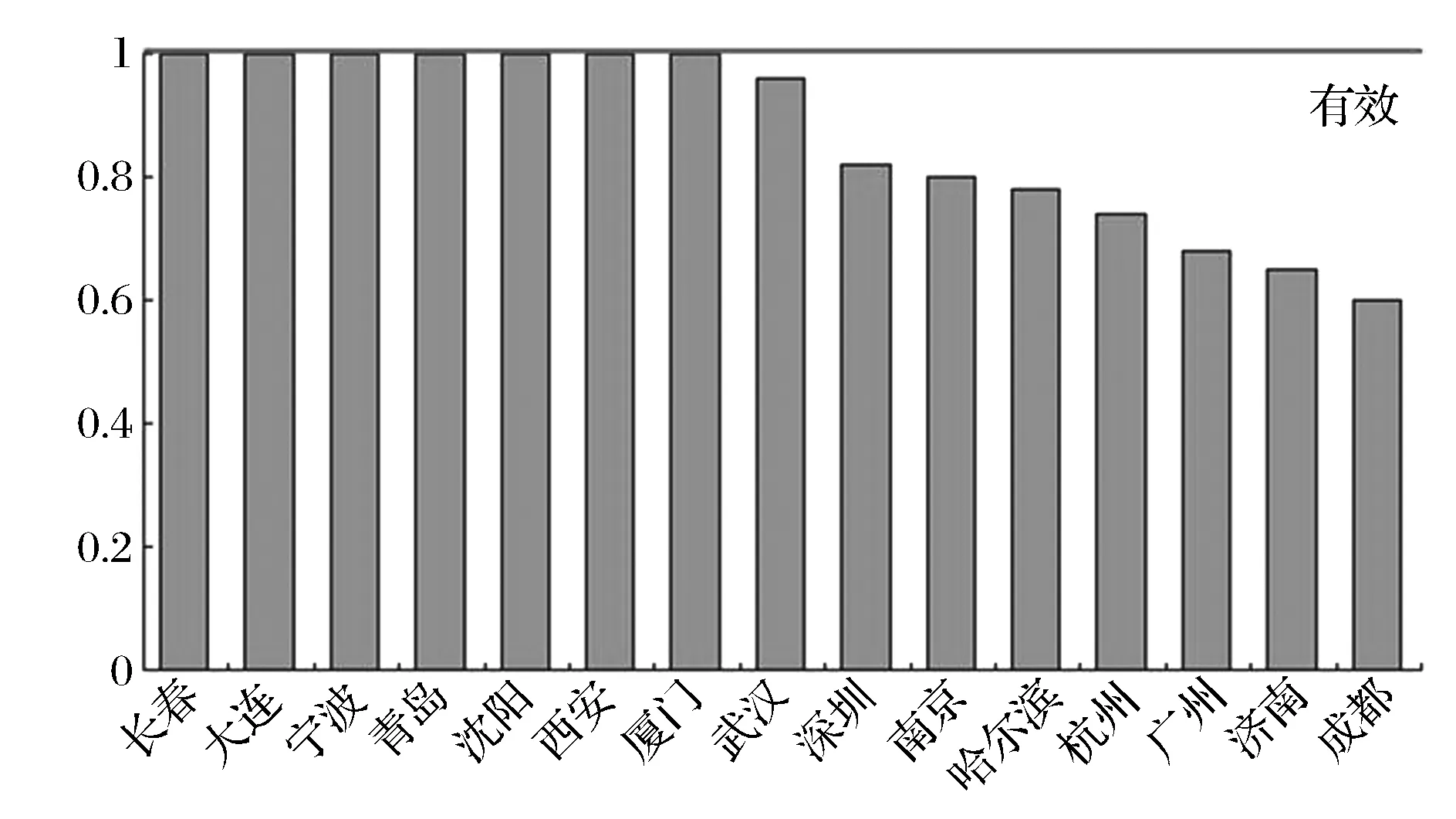
图3 副省级城市的总体投入效率TE

4.2.2 投入冗余和产出不足的测算及分析

针对表3第8-15行的8个未能达到效率最优的副省级城市，测算投入冗余和产出不足。

(1)投入冗余si-和产出不足si+的计算

将表3第3-5列的数据作为投入指标，第6-8列的数据作为产出指标数据代入式(1)，得到投入冗余量列入表4第3、5、7列第1-8行，产出不足量列入表4第9、11、13列第1-8行。

(2)投入冗余率ri-和产出不足率ri+的计算

根据上述得到的投入冗余量和产出不足量，得到投入冗余率列于表4第4、6、8列前8行，产出不足率列于表4第10、12、14列前8行。表4第9行是平均不足量和平均不足率。

将表4中投入冗余率和产出不足率高于平均值的副省级城市用“√”进行标记，如表5所示。

(3)投入冗余和产出不足的结果分析

由表4可以得到以下结论：

①“规模以上工业企业R&D经费支出”、“财政科技经费投入”的平均投入冗余率较高，分别为27.11%、28.35%，有将近30%的投入未有效地转化为成果产出，说明副省级城市在这两项上存在严重的投入无效。

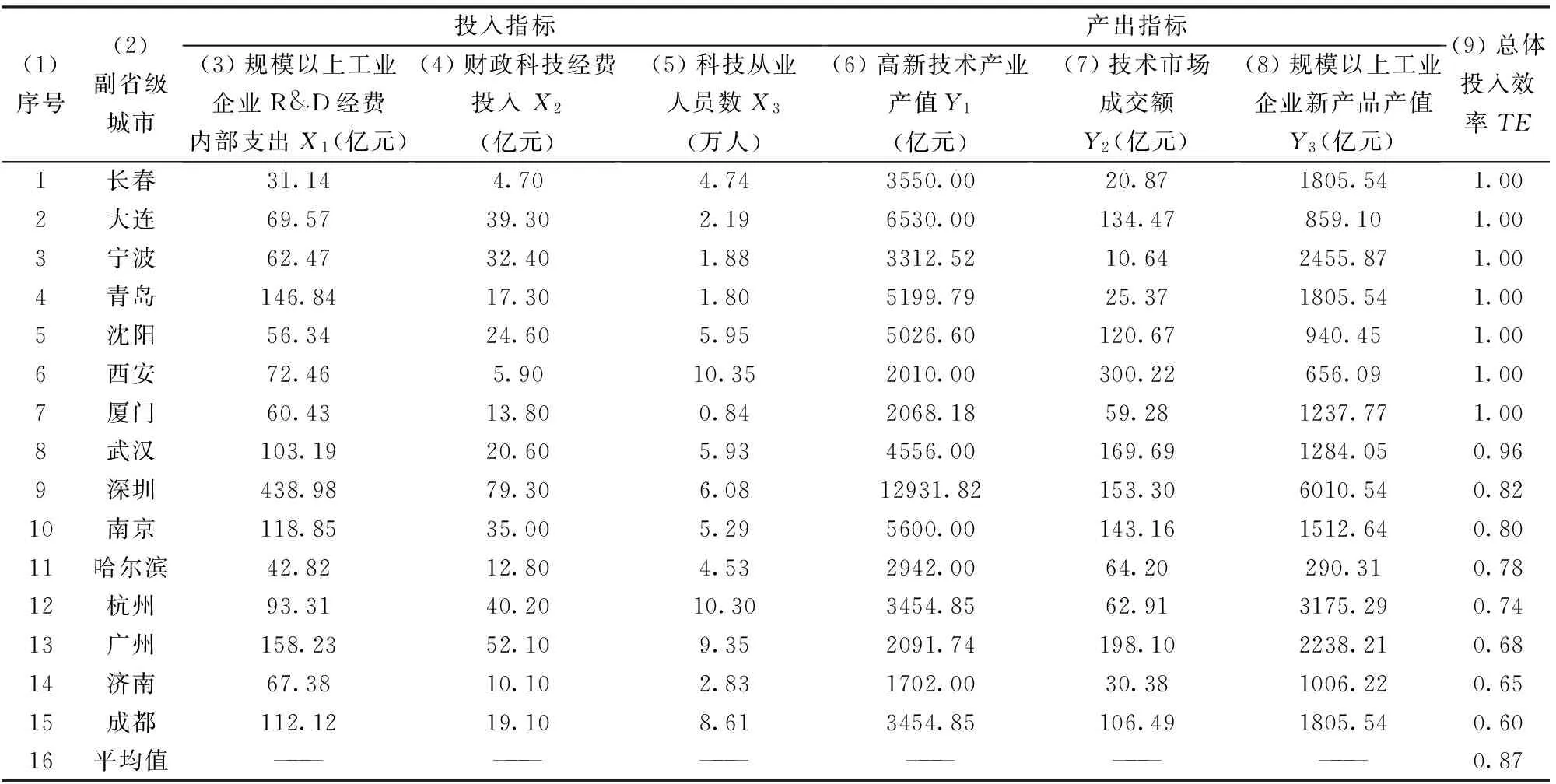
表3 投入产出指标的原始数据及总体投入效率

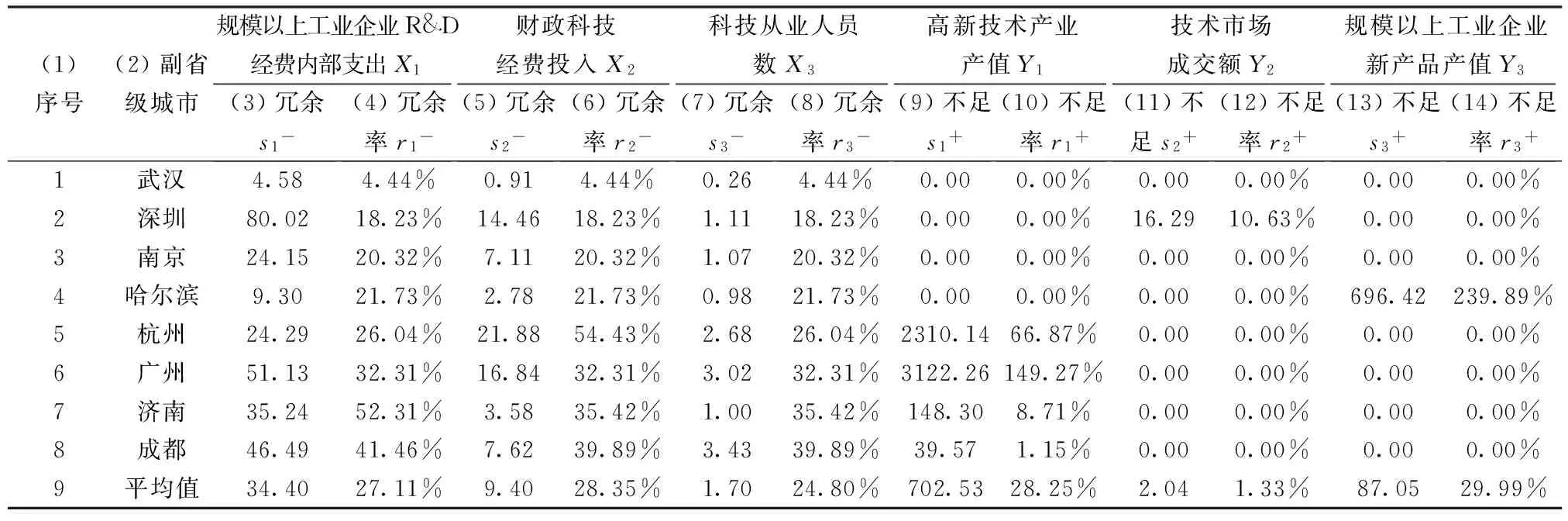
表4 投入冗余和产出不足

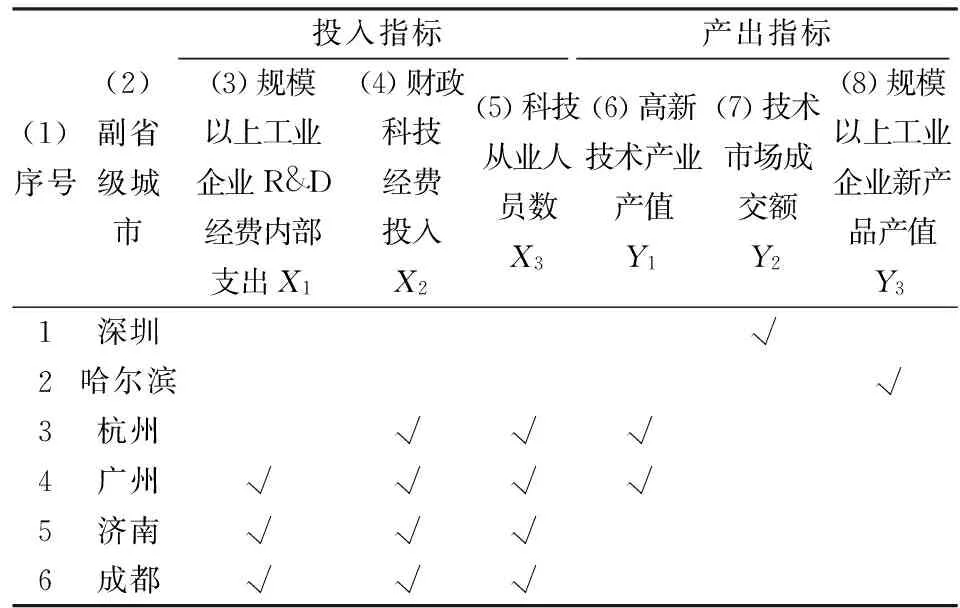
表5 投入冗余率和产出不足率高于平均值的副省级城市

②“高新技术产业产值”、“规模以上工业企业新产品产值”的平均产出不足率较高，分别为28.25%、29.99%，有将近30%的科技成果没有成功产出，说明副省级城市在这两项上存在严重的产出不足。

由表5可得到以下结论：

①广州的投入冗余和产出不足现象最为严重。广州在全部的投入指标的冗余率都超过平均值。而且广州在“高新技术产业产值”上存在超高的产出不足率，高达149.27%。

②济南、成都在全部科技投入指标上都存在较高的冗余率。盲目的科技投入造成济南、成都大量的资源浪费。

③杭州不仅在“财政科技经费投入”、“科技从业人员”的投入上存在较高的冗余，而且在“高新技术产业产值”上存在较高的不足。

④哈尔滨的“规模以上工业企业新产品产值”的产出不足最为严重、高达239.89%。应促进“规模以上工业企业新产品产值”的产出。

4.3 纯技术效率评价

4.3.1 纯技术效率PTE的测算

针对总体投入效率TE<1的8个副省级城市，测算纯技术效率PTE、规模效率SE，进一步分析导致总体投入效率未达到有效的原因。

在表3第1-15行中：将第3-5列的数据作投入指标的数据，第6-8列的数据作为产出指标的数据代入式(4)，求得武汉、深圳、南京、哈尔滨、杭州、广州、济南、成都的纯技术效率PTE，列于表6第3列前8行。

4.3.2 纯技术效率的结果分析

由表6第3列的纯技术效率可知：

①长春、大连、宁波、青岛、沈阳、西安、厦门、武汉、深圳、杭州的纯技术效率为1，均达到纯技术效率有效，技术和管理水平已达到最佳。

②南京、哈尔滨、广州、济南、成都的纯技术效率未达到1，说明纯技术效率未达到有效，技术和管理水平存在滞后现象。

4.4 规模效率评价

4.4.1 规模效率SE的测算

将表3第9列第8-15行的总体投入效率TE，除以表6第3列前8行的纯技术效率PTE，得到规模效率SE，列于表6第4列前8行。表6第9行第3、4列为纯技术效率、规模效率的平均值。

4.4.2 规模收益递增/递减的判定

在表3第1-15行：将第3-5列的数据作投入指标的数据，第6-8列的数据作为产出指标的数据代入式(1)，求得系数和，列于表6第6列。

将表6第6列的系数和、第3列前8行的纯技术效率PTE代入公式(6)，得到规模收益系数Kp，结果列于表6第7列。判定结果如表6第8、9列所示。

4.4.3 规模效率评价的结果分析

由表6第4、8、9列的规模效率可知：

①武汉、深圳、南京、杭州、广州、成都因投入规模过大，导致其规模效率没有达到有效。由表6第4列可知，武汉、深圳、南京、杭州、广州、成都的规模效率都未达到有效，说明其投入模型不合理。由表6第8、9可知，其规模收益是递减的，说明现有的投入规模过大导致了其规模效率偏低。

②哈尔滨、济南因投入规模过小，导致其规模效率没有达到有效。由表6第4列可知，哈尔滨、济南的规模效率都未达到有效，说明其投入规模不合理。又由表6第8、9可知，哈尔滨、济南的规模收益是递增的，说明现有的投入规模过小导致了哈尔滨、济南的规模效率偏低。

③长春、大连、宁波、青岛、沈阳、西安、厦门的投入规模合理。由4.3.1节中(1)可知，长春、大连、宁波、青岛、沈阳、西安、厦门的规模效率SE均为1，说明其投入规模合理。

4.5 三种效率评价的结论归纳

根据4.2节总体投入效率价、4.3节纯技术效率价和4.4节规模效率评价，可以得到以下结论：

①长春、大连、宁波、青岛、沈阳、西安、厦门实现投入有效，总体投入效率、纯技术效率、规模效率均达到有效，说明这7个副省级城市的技术和管理水平达到最佳，而且投入规模合理。

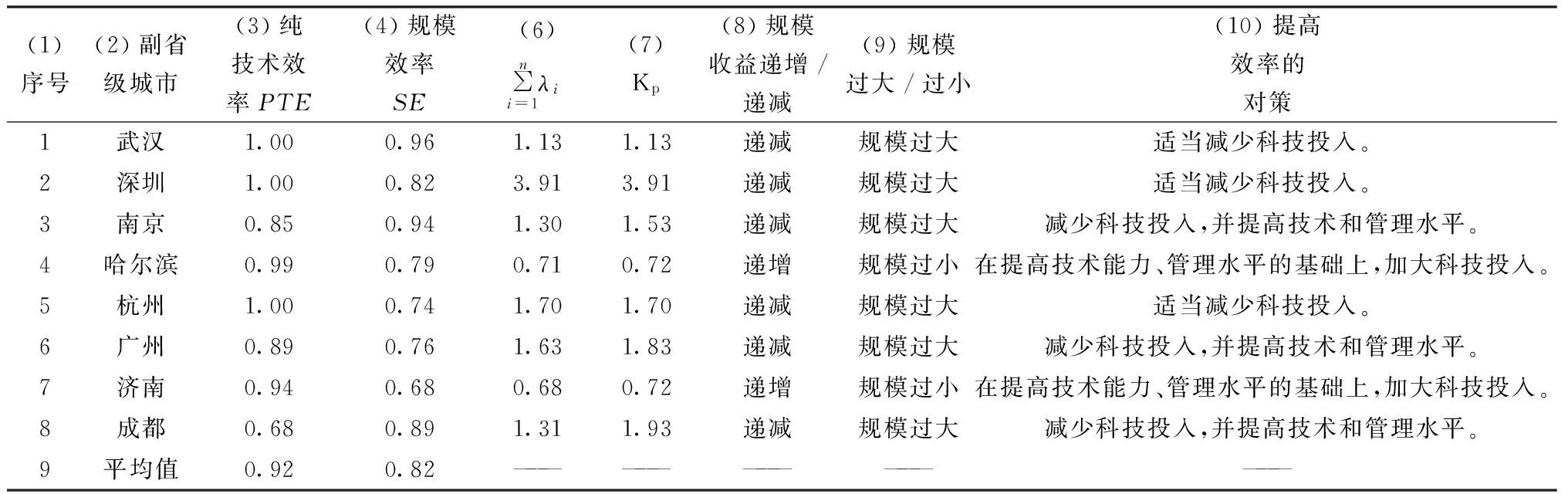
表6 纯技术效率、规模效率的测算结果以及规模收益的判定

②武汉、深圳、杭州的纯技术效率达到有效，但规模效率未达到有效导致了其总体投入效率无效，且武汉、深圳、杭州的投入规模过大，应该减少投入。由表6第1、2、5行可知，武汉、深圳、杭州的纯技术效率达到1，而规模效率均小于1且规模收益递减，所以武汉、深圳、杭州虽然技术管理水平达到最佳，但规模效率未达到有效、投入规模过大导致武汉、深圳、杭州的效率不高。

对武汉、深圳、杭州的启示：由于企业和政府对科技投入过剩，导致了大量投入无法有效利用、“规模以上工业企业R&D经费内部支出”等以企业为主体的科技投入存在冗余，所以应当适当减少科技投入来提高效率。

③哈尔滨、济南的纯技术效率和规模效率都未达到有效，共同导致了其总体投入效率偏低，且哈尔滨、济南的投入规模过小，应该适当增加投入。由表6第4、7行可知，哈尔滨、济南的纯技术效率和规模效率都未达到1，且规模收益递增，所以，技术能力、管理水平落后以及投入规模过小是导致哈尔滨、济南效率不高的主要原因。

对哈尔滨、济南的启示：由于技术管理能力落后以及投入规模过小，导致大量投入无法有效利用。所以哈尔滨、济南不能盲目加大投入，应该在提高技术能力、管理水平基础上，再加大科技投入。

④南京、广州、成都的纯技术效率和规模效率都未达到有效，共同导致了其总体投入效率偏低，且南京、广州、成都的投入规模过大，应该减少投入。由表6第3、6、8行可知，南京、广州、成都的纯技术效率和规模效率未达到1，且规模收益递减，所以技术能力、管理水平落后以及投入规模过大是导致南京、广州、成都效率不高的主要原因。

对南京、广州、成都的启示：由于企业和政府对科技投入过剩，加之技术和管理水平的滞后，使大量投入未能有效利用，所以南京、广州、成都应该减少科技投入，并提高技术和管理水平，从而提高效率。根据上述分析结果，提高效率的对策列于表6第10列。

4.6 影响科技创新效率的关键因素萃取

4.6.1 对比模型的总体投入效率TE

关键指标萃取的基础模型和6个对比模型如表2所示。基础模型的总体投入效率TE0列于表7第3列，其值来源于表3第9列。与4.2中的实证过程同理，得到对比模型的效率值TEi，列于表7第4、6、8、10、12、14列。

4.6.2 关键指标的萃取过程

(1) 6个对比模型对应的t统计量的计算

将表7第3列基础模型效率TE0分别减去表7对比模型效率TE1、…、TE6，得到基础模型与6个对比模型的效率差值dj1、…、dj6，列入表7第5、7、9、11、13、15列，并代入式(9)，分别得到6个对比模型的t统计量值ti，列于表7第16行。

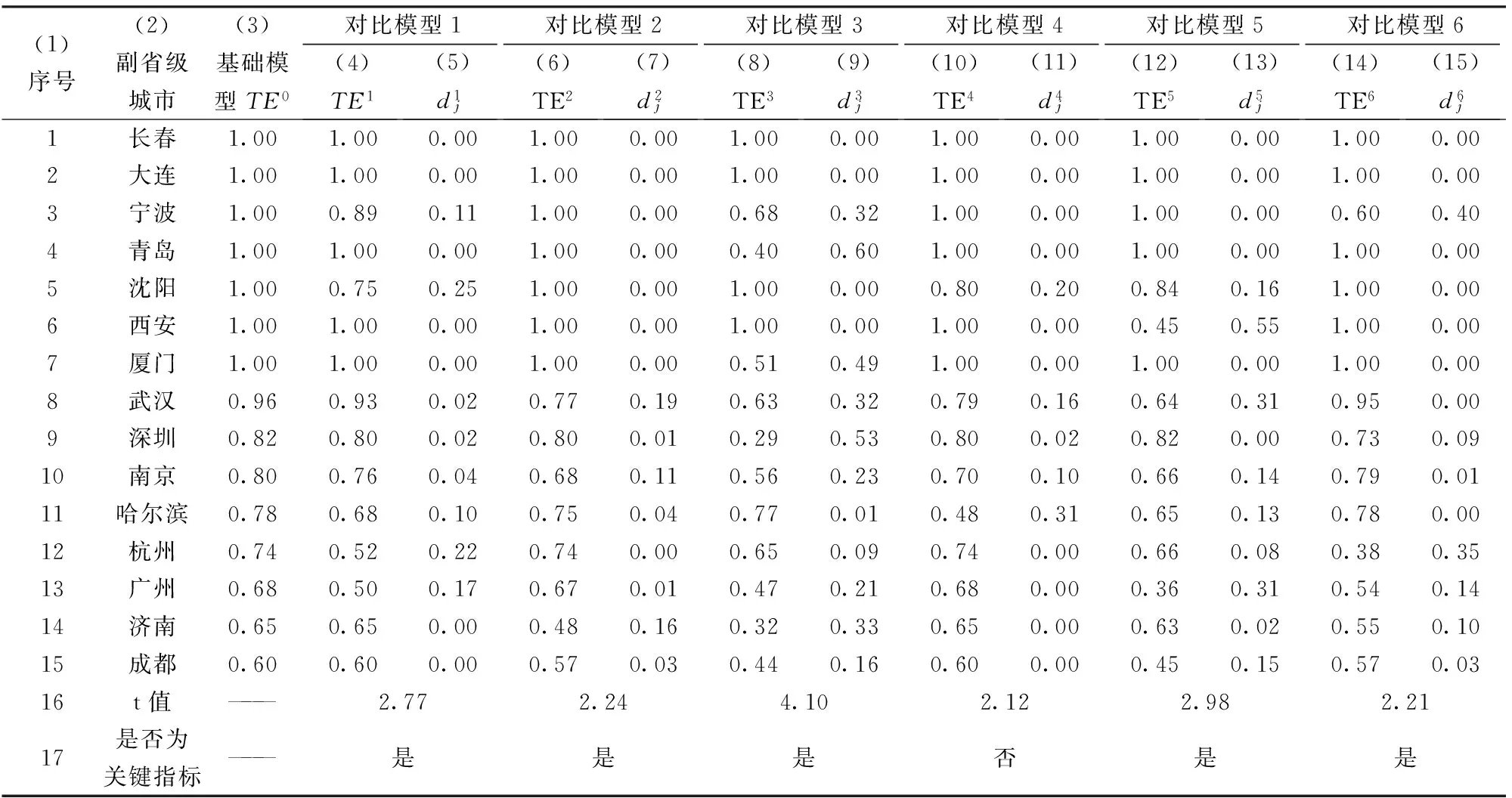
表7 基础模型、对比模型的总体投入效率及差值

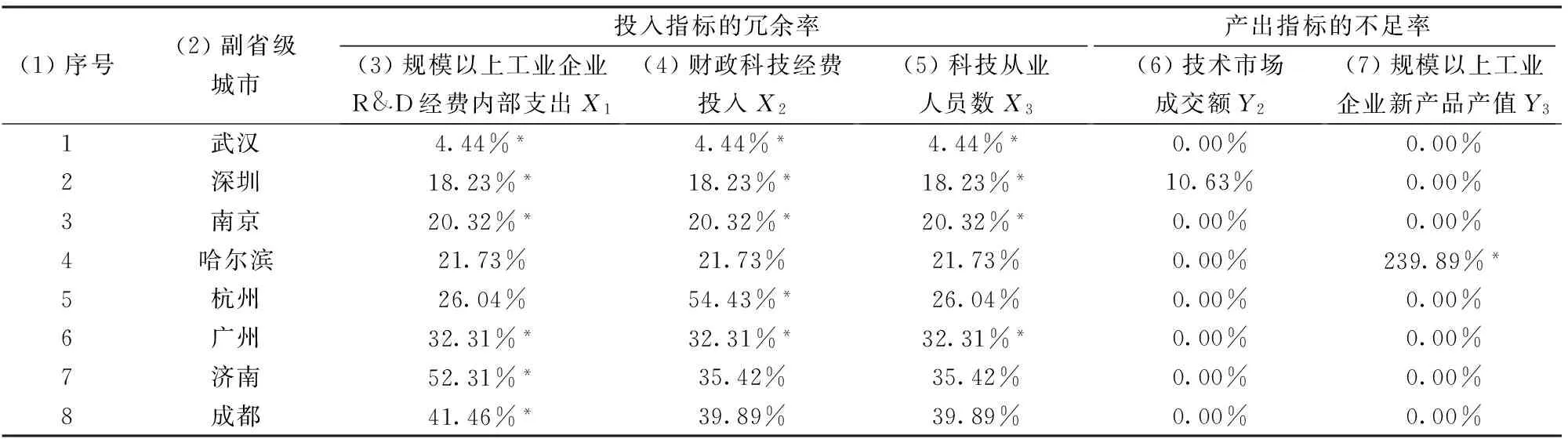
表8 副省级城市关键指标的冗余率、不足率及关键问题

(2)关键指标的判别

选取显著性水平α=0.05[16]，由t分布临界值表可查得t0.05(14)=2.15。由于t1、…、t6均大于2.15，所以指标X1、X2、X3、Y2、Y3能够显著影响以企业为主体的科技创新效率、即为关键指标。

由于t4=2.12<2.15，所以指标Y1不能够显著影响以企业为主体的科技创新效率、不是关键指标。关键指标的判别结果列于表7第17行。

利用萃取的关键指标计算效率：由表2第5行可知，“对比模型4”是在全部投入产出指标基础上仅剔除指标Y1、这一个“非关键指标”后的效率模型，则说明“对比模型4”就是利用萃取的五个关键指标计算效率的模型，结果如表7第7列所示。

“对比模型4”与“基础模型”效率差值进行t检验的结果如表7第11列第16行所示。由于t4=2.12<临界值2.15，则t检验不通过。说明利用DEA模型的全部指标与利用萃取的关键指标计算的效率值排序虽然不完全一样，但在统计学上两者的差别不显著，故利用全部指标与利用萃取的关键指标计算的效率值排序大体上是一致的。

4.7 关键问题的剖析

(1)关键问题的选取需要同时满足以下标准:

标准一：该指标是表7最后一行中的关键指标。只有针对显著影响效率的关键指标进行剖析，才能找到快速提高效率的方式。

标准二：该指标的投入冗余率或产出不足率最大。副省级城市在该指标上存在的投入无效或产出不理想现象是最为严重的。

(2)不同副省级城市的关键问题

表8是关键指标的冗余率或不足率，数据来源于表4第4、6、8、12、14列。表8每一行中找出冗余率或不足率最大的指标，用“*”标记，该指标为影响该副省级城市效率不足的关键问题。

由表8的关键问题可知，导致不同副省级城市效率偏低的关键问题大相径庭。具体如下：

①济南、成都效率偏低的关键问题是“规模以上工业企业R&D经费内部支出”的冗余率过大。该指标的投入无效是济南、成都效率偏低的关键问题。增大“规模以上工业企业R&D经费内部支出”的利用率，能快速提高济南、成都的科技投入产出效率。

②杭州效率偏低的关键问题是“财政科技经费投入”的冗余率过大。该指标的投入无效是杭州效率偏低的关键问题。增大“财政科技经费投入”的利用率，能快速提高杭州的科技投入产出效率。

③哈尔滨效率偏低的关键问题是“规模以上工业企业新产品产值”的产出不足超高，高达239.89%。增大“规模以上工业企业新产品产值”的产出，能快速提高哈尔滨的科技投入产出效率。

④武汉、深圳、南京、广州效率偏低的关键问题是“规模以上工业企业R&D经费内部支出”、“财政科技经费投入”、“科技从业人员数”三项投入都存在冗余。同时增大该三项投入指标的利用率，能快速提高武汉、深圳、南京、广州的科技投入产出效率。

5 结语

5.1 主要结论

(1)以企业为主体科技创新效率的关键指标为规模以上工业企业R&D经费内部支出X1、财政科技经费投入X2、科技从业人员数X3、技术市场成交额Y2、规模以上工业企业新产品产值Y3。

(2)导致不同副省级城市效率偏低的关键问题大相径庭。例如杭州效率偏低的关键问题是“财政科技经费投入”的冗余率过大。而哈尔滨效率偏低的关键问题是“规模以上工业企业新产品产值”的产出不足超高。

(3)长春、大连、宁波、青岛、沈阳、西安、厦门以企业为主体的科技创新实现投入有效，纯技术效率、规模效率均达到有效。

5.2 创新与特色

(1)通过将保留所有指标的DEA效率测算模型作为基础模型，将逐一剔除单个指标后的DEA效率测算模型作为对比模型。利用t检验，依次检验基础模型与每个对比模型的总体投入效率TE是否存在显著差异。若差异显著，则对比模型中剔除的指标为显著影响效率的关键指标。改变现有研究仅仅通过数据包络分析(DEA)测算效率、无法萃取影响效率的关键因素的弊端。

(2)通过效率评价的投入和产出指标，体现以企业为主体的科技创新，即以“规模以上工业企业R&D经费内部支出”、“财政科技经费投入”、“科技从业人员数”为投入指标，反映企业科技经费投入、企业人力投入以及政府对企业的科技经费投入；以“高新技术产业产值”、“规模以上工业企业新产品产值”、“技术市场成交额”为产出指标，反映高新技术企业产值、企业新产品转化能力以及技术合同产出。弥补现有研究忽略企业的主体地位的弊端。

(3)通过数据包络分析(DEA)的BCC模型，测算规模效率SE，判断副省级城市的投入规模是否合理。进而判别规模报酬是递增还是递减的，确定现有的投入规模是过小/过大，相应地采用增大投入/减少投入的方式提高效率，从而找到与投入规模对应的提高效率方式。

[1] 中国经济网. 十八大三中全会《决定》、公报、说明(全文)[EB/OL]. [2013-11-18].http://www.ce.cn/xwzx/gnsz/szyw/201311/18/t20131118_1767104.shtml.

[2] 中国行业研究网. 2014年全国政协“一号提案”正式出炉[EB/OL]. [2014-03-03].http://www.chinairn.com/news/20140303/0919103.html.

[3] 杜娟, 霍佳震. 基于数据包络分析的中国城市创新能力评价[J]. 中国管理科学, 2014, 22(6): 85-93.

[4] 晏蒙, 孟令杰. 基于DEA方法的中国工业科技创新效率分析[J]. 中国管理科学, 2015,23(S1):77-82.

[5] 李洪伟, 任娜, 陶敏, 等. 基于三阶段DEA的我国高新技术产业投入产出效率分析[J]. 中国管理科学, 2012, 20(S1): 126-131.

[6] 范斐, 杜德斌, 李恒. 区域科技资源配置效率及比较优势分析[J]. 科学学研究, 2012, 30(8): 1198-1205.

[7] Sueyoshi T, Goto M. A use of DEA-DA to measure importance of R&D expenditure in Japanese information technology industry [J]. Decision Support Systems, 2013, 54(2): 941-952.

[8] Odeck J, Brathen S. A meta-analysis of DEA and SFA studies of the technical efficiency of seaports: A comparison of fixed and random-effects regression models [J]. Transportation Research Part A: Policy and Practice, 2012, 46(10): 1574-1585.

[9] Lafarga C V, Balderrama J I L. Efficiency of Mexico's regional innovation systems: an evaluation applying data envelopment analysis (DEA)[J]. African Journal of Science Technology Innovation & Development, 2015, 7(1):36-44.

[10] 蒋仁爱, 高昌林, 冯根福. 中国研究机构的科技资源利用效率评价研究[J]. 统计研究, 2013, 30(6):19-29.

[11] 戚湧, 郭逸. 基于SFA方法的科技资源市场配置效率评价[J]. 科研管理, 2015, 36(3):84-91.

[12] 肖文, 林高榜. 政府支持、研发管理与技术创新效率——基于中国工业行业的实证分析[J]. 管理世界, 2014,(4): 71-80.

[13] Xie Xin, Liu Fangfang. Analysis on regional technology innovation efficiency evaluation and influence factors in China[J]. International Journal of Business & Management, 2015, 10(3).

[14] Afzal M N I. An empirical investigation of the National Innovation System (NIS) using Data Envelopment Analysis (DEA) and the TOBIT model[J]. International Review of Applied Economics, 2014, 28(4):1595-1598.

[15] Hu Jinli, Yang C H, Chen C P. R&D Efficiency and the national innovation system: An international comparison using the distance function approach [J]. Bulletin of Economic Research, 2014, 66(1): 55-71.

[16] European Commission. Innovation union scoreboard 2014 [R]. European Commission,2014.

[17] World Economic Forum (WEF).The global competitiveness index 2013-2014: Country profile highlights [R].World Economic Forum, 2013

[18] 中国科技发展战略研究小组．中国区域创新能力报告2011：区域创新与战略性新兴产业发展[M]．北京：科学出版社，2011．

[19] 中国国家统计局. 2012年全国科技经费投入统计公报[R]. 国家统计局,2013.

[20] 中国技术市场管理促进中心. 2013全国技术市场统计年度报告[R]. 中国技术市场管理促进中心, 2013.

[21] 马占新. 数据包络分析模型与方法[M]. 北京:科学出版社, 2010.

[22] 高惠璇.应用多元统计分析[M]. 北京：北京大学出版社, 2005.

The Efficiency Evaluation of Technology Innovation Centered on Enterprise Based on DEA and T Test

LI Hong-xi, CHI Guo-tai

(Faculty of Management and Economics, Dalian University of Technology, Dalian 116024,China)

The efficiency evaluation of technology innovation is aimed to measure the output of technology, efficiency of resource utilization centered on enterprise and find out important factors of technology innovation efficiency. The enterprise is the main part of technology input and output in this research. Data Envelopment Analysis is used to do empirical analysis of 15 sub-provincial cities in China. The pure technology efficiency and scale efficiency is measured to determine the scale is big or small. By screening the important factors that signally influence technology efficiency, the key problem of every sub-provincial city is find out. The innovations and characters: firstly, in this paper the efficiency evaluation model included all indicators is the basic model and the efficiency evaluation model without one indicatorXiis the comparison model. By t test, it is verified if the efficiency difference between basic model and comparison model is significant. If the difference is significant, the indicatorXiis the key factor. It changes the existing research can’t screen the key indicators by DEA. Secondly, empirical result shows that the key indicators include “R&D expenses of industrial enterprises above designated size” “financial funds to technology” “technology professionals” “new products output of industrial enterprises above designated size” “technical market turnover”. Thirdly, empirical results show that the reasons why technology efficiency is low for different sub-provincial cities are different.

technology innovation; technology efficiency; DEA; t test; key indicators

1003-207(2016)11-0109-11

10.16381/j.cnki.issn1003-207x.2016.11.013

2015-09-13；

2016-03-01

国家自然科学基金资助项目(71471027，71171031)；大连市政协项目(2014-03)

迟国泰(1955-)，男(汉族),黑龙江海伦人，大连理工大学管理与经济学部金融学教授,博士生导师,管理科学与工程博士, 研究方向：复杂系统评价,E-mail:chigt@dlut.edu.cn.

C931;F204

A