惯性导航传递对准技术发展现状与趋势

宋嘉钰，杨黎明，李东杰

(中国工程物理研究院 电子工程研究所，四川 绵阳　621000)



惯性导航传递对准技术发展现状与趋势

宋嘉钰，杨黎明，李东杰

(中国工程物理研究院 电子工程研究所，四川 绵阳621000)

摘要：惯导技术具有完全自主、高度隐蔽、数据频率高等特性，因而在军事上得到广泛应用。传递对准技术是惯性导航的关键技术，对于保证精确制导武器搭载的以惯导为主的导航系统的精度具有重要意义。介绍了传递对准技术的基本原理，总结了传递对准技术中系统误差模型、匹配方式、可观测性分析、误差补偿、滤波方法等方面的理论和方法。归纳了近年来传递对准技术研究的进展，探讨了传递对准技术未来的发展方向。

关键词：惯性导航；传递对准；匹配方法；可观测性

Citation format:SONG Jia-yu, YANG Li-ming, LI Dong-jie.Development of Transfer Alignment for Inertial Navigation Systems[J].Journal of Ordnance Equipment Engineering,2016(2):139-143.

初始误差是惯导系统的一个重要误差来源，所以初始对准的精度直接影响到惯导系统的性能[1]。惯导系统的初始对准主要有自对准和传递对准两种方式，传递对准所需时间较短，对惯性器件的要求较低，因而对于缩短对准时间和降低惯导系统成本更有利。诸多学者为了提高传递对准的精度、减少对准时间以及提高算法的鲁棒性展开了大量研究。

传递对准是用高精度的主惯导(master INS,MINS)导航信息对低精度的子惯导(slave INS，SINS)进行初始对准的过程，一般包括粗对准和精对准两个过程。如图1所示，首先进行粗对准，利用主惯导提供的导航信息对子惯导进行初始装订，装订完成后，子惯导开始导航解算，利用主子惯导提供的信息，通过传递对准滤波器估计出失准角等误差参数，再相应的对子惯导进行修正，从而完成精对准[2]。

1传递对准的模型

传递对准过程中，系统状态方程和观测方程的基本形式分别由惯导系统误差方程和匹配方式决定。为了确定滤波器能否收敛，一般还要先对模型进行可观测性分析。

在传递对准的模型中，状态方程的基本形式是由惯导系统误差模型决定的。

为了建立姿态误差模型，在失准角满足小角度假设的情况下，传统的角误差模型如φ角误差模型和ψ角误差模型得到了广泛的应用。Rogers[3]对φ角误差模型和ψ角误差模型进行了对比，并在文献[3]中指出φ角误差模型的传递对准效果优于ψ角误差模型。

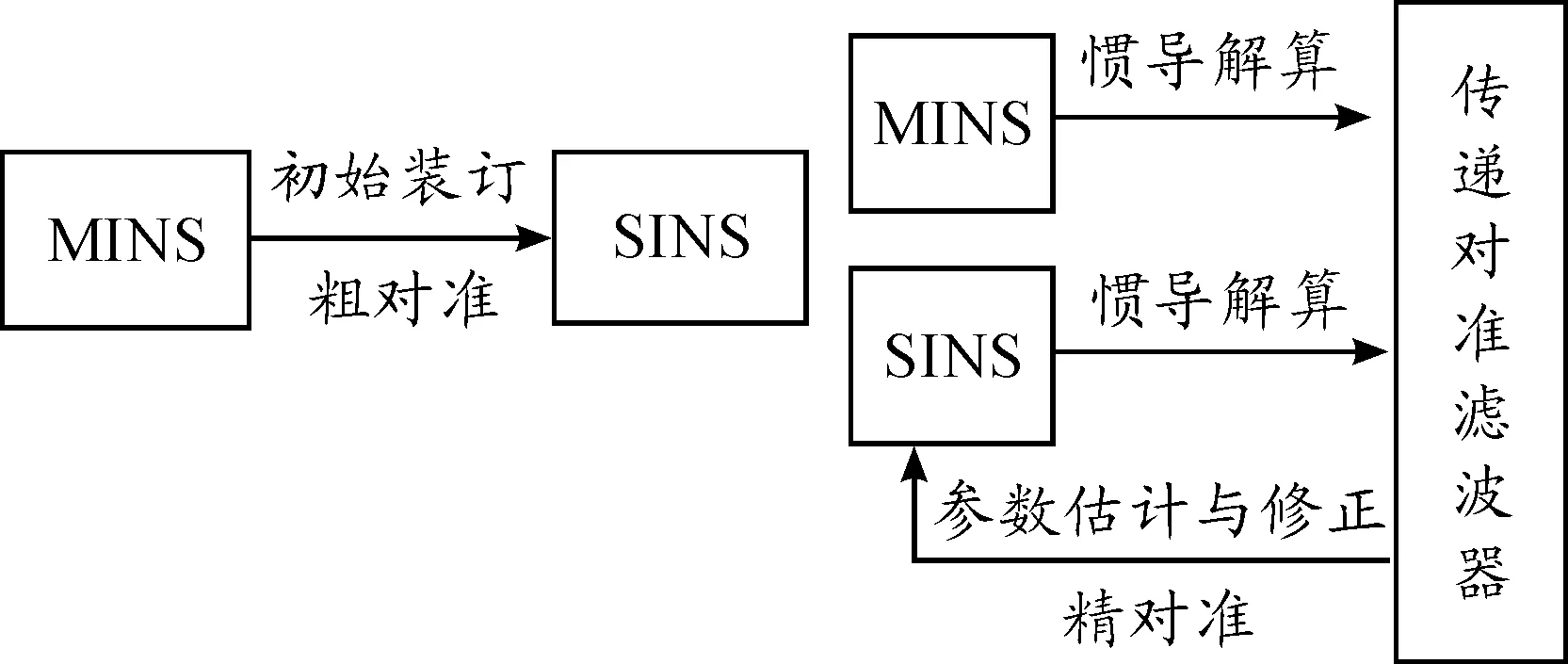
图1　传递对准的基本流程

Kain和Cloutier[4]引入了量测失准角的概念，提出了快速传递对准方程，量测失准角作为载体坐标系下定义的失准角，代表主、子惯导载体坐标系之间的姿态误差，并且可以直接作为观测量，很大程度上简化了传递对准方程。陈凯[5]就快速传递对准方程和传统传递对准方程进行了分析，证明了快速传递对准方程是传统传递对准方程的一种特殊形式，二者具有一致性。

大失准角的情况下，由于失准角不再满足小角度假设，采用一阶近似的角误差模型会导致较大的误差，而若不采用小角度假设，则可能会导致姿态矩阵的奇异性限制以及大量繁琐的三角函数计算。在这种情况下，四元数姿态误差模型由于其可全姿态工作成为了一种有效解决方法。熊芝兰[6]推导了基于乘性四元数和加性四元数的两类非线性误差模型，并用于仿真实现了大失准角条件下的传递对准。周卫东[7]和陈雨[8-9]分别采用乘性四元数建立非线性传递对准模型，并且实现了大失准角条件下快速传递对准的仿真。

在传递对准中，惯性器件误差一般采用数学模型表示。在早期的研究中，在建模时大多只是考虑了陀螺的漂移[10-11]，在后来的研究中还引入了加速度计零偏、加速度计和陀螺的刻度系数误差等参数[12-15]。针对传递对准中失准角状态变量可观测度高，惯性器件的可观测度低的问题，林敏敏等[14]提出了一种分级标定的方法，将三个失准角的估计值反馈回惯导系统进行分级修正，通过不断修正系统的滤波模型，可实现惯性器件误差的准确标定。

2匹配方法

匹配方法研究一直以来都是传递对准研究的基本问题，根据传递对准过程中所用观测数据的不同对匹配方法进行分类。匹配方法按照匹配参数的来源分为测量参数匹配和计算参数匹配。按照匹配量的性质分为线运动参数匹配、角运动参数匹配以及组合参数匹配。

匹配方法会影响传递对准的速度、精度和可观测性；同时，不同的匹配方式在计算量大小和对辅助机动的依赖程度上也有所差异。一般来说，计算参数匹配在传递对准精度上优于测量参数匹配，测量参数匹配在收敛速度上优于计算参数匹配。

单一匹配的方式，例如速度匹配，虽然由于杆臂效应更易于补偿，同时在挠曲变形和惯性器件测量噪声的积分平滑上具有优势而获得的广泛的关注与应用，但是同时也存在方位失准角、安装误差角和挠曲变形角估计效果较差等不足[16]，为改善滤波估计效果往往需要一些复杂的辅助机动，但这又影响了传递对准的快速性；而姿态匹配虽然收敛速度快，但是对于速度的估计效果则较差。

Kain和Cloutier[4]于1989年提出 “速度+姿态”的组合匹配方法，同时利用姿态匹配和速度匹配的优势，以提高传递对准性能。采用这种匹配方法的传递对准方案在飞行实验中取得了传递对准时间10 s以内，对准精度达到1 m rad的结果[17]。在此之后，综合利用角运动参数匹配优势和线运动参数匹配优势的这一类的匹配方法得到了很大发展，“速度+姿态角”匹配[4,14]、“速度+姿态角变化量”匹配[18]、“速度+姿态矩阵”匹配[19]、最优姿态匹配[15,20]等匹配方法相继被提出。

陈凯[21]从理论上证明了“姿态角匹配法”、“姿态矩阵匹配法”、“量测失准角匹配法”和“最优姿态匹配法”的统一性。与传统的传递对准中姿态匹配需要利用主、子惯导解算的结果来构建观测量不同，刘镇波等[22]提出利用主、子惯导的输出直接解算其相对姿态并用于构建观测量的方法，仿真结果表明，在子惯导陀螺精度为1°/h且只需要估计相对姿态误差的情况下，只需要S机动辅助，无需子惯导进行惯导解算，即可在获得10s内3′的对准精度。

3可观测性分析

在设计传递对准滤波器之前，要进行可观测性分析，确定滤波器能否收敛。为此，首先需要确定系统是否是完全可观测；其次，对不完全可观测系统，确定哪些状态变量独立可观测，哪些变量非独立可观测，以及哪些状态变量或其线性组合不可观测。

在传递对准过程中，载体处于运动状态，传递对准的模型只能近似为线性时变随机系统，采用传统的线性系统的分析方法来分析其可观测性存在很大不足。Goshen-Meskin和Bar-Itzhack[23-24]提出一种分段线性定常系统(piece-wise constant system,PWCS)的可观测性分析理论，用提取的可观测矩阵(Stipped Observability Martrix,SOM)取代总的可观测性矩阵(Total Observability Martrix,TOM)进行系统的可观测性分析。

可观测性的分析的结果只能对系统状态变量的可观测情况进行定性分析，而无法量化状态变量的可观测程度。而状态变量的可观测程度才能反映利用滤波器对状态变量进行估计时的收敛速度和精度。

1983年，Ham[25]提出利用卡尔曼滤波器的估计误差协方差矩阵来计算可观测度，通过协方差矩阵的特征值和特征向量来描述系统状态变量的可观测度；该方法的缺陷在于可观测度的计算需要在卡尔曼滤波运算后才能进行，且计算量较大。程向红等[26]提出一种基于时变系统可观测性矩阵的奇异值分解方法。文献[27]反例证明奇异值分解的可观测度分析方法存在理论缺陷，文献[28]分析了特征值分解法和奇异值分解法的等价性，并从理论分析了奇异值分解法存在的不足。基于PWCS理论，孔星炜[29]提出用可观测阶数和相对可观测度来量化分析可观测性。陈雨[30]提出一种从误差衰减角度定义的可观测度分析指标。

目前各种可观测度的分析方法，尚没有一个统一的量纲定量地描述可观测度；同时不同的分析方法中用于量化分析可观测度的参数与状态变量之间一一对应的关系也缺乏理论证明。

4主要误差与补偿

在实际的传递对准过程中，除了模型本身具有的误差以外，还存在多种系统误差和随机误差，会对传递对准的性能造成影响，这些误差主要包括挠曲运动、杆臂效应和时间延迟带来的误差。

4.1挠曲运动误差及补偿

在传递对准过程中，载体并不是绝对的刚体，载体挠曲运动会使主子惯导系统的惯性器件测量不同的运动信息，从而为传递对准带来较大误差。但挠曲运动同时受到结构、载荷分布和运动条件等很多因素的影响，对其精确建模十分困难。为此，很多相关研究采用一些近似模型来提高传递对准精度。Kain和Cloutier[4]将机翼结构振动引起的高频挠曲运动视为三阶Gauss-Markov过程，构造真实模型。同时为了增加传递对准的快速性，通过真实模型的协方差分析结果来确定注入白噪声的强度，用白噪声代替真实模型中有关挠曲运动的变量，通过这种方法补偿挠曲运动以及增加滤波器的鲁棒性。Spalding[31]在Kain[41]等的工作基础上，将机翼挠曲运动分解为准静态挠曲和高频挠曲两种模态，均视为三阶Gauss-Markov过程，其中准静态挠曲模态选择了一个随着机动运动而减小的时间常数，用以逼近机翼在机动运动中的真实挠曲过程,为了提高快速性，同样在滤波器中删除了挠曲有关变量。此外，还有学者提出通过增加过程噪声和测量噪声水平，并应用较高幅度与强度的机动来抑制某些情况下的挠曲运动干扰[32-33]。刘锡祥[34]和王跃钢[35]在传递对准滤波器设计中引入H∞滤波，将挠曲运动作为量测噪声进行处理，提高了算法的鲁棒性和精度。

4.2杆臂效应误差与补偿

当刚性载体存在相对于惯性空间的角运动时，由于主子惯导所处位置不同，主子惯导系统中的加速度计会敏感到不同的加速度，从而导致解算出不同的速度，这就是传递对准中的杆臂效应。杆臂效应会导致主子惯导解算出的速度、姿态等信息出现差异，进而影响传递对准的性能。

杆臂效应的补偿可以分为滤波补偿法与计算补偿法(力学补偿法)两类方法。滤波补偿法的原理是利用载体本身运动的加速度与干扰加速度在频率分布上不同，通过对加速度计的输出信号进行频谱分析，设计合适的滤波器对信号进行滤波处理，减小干扰加速度的影响。计算补偿法则是通过计算出杆臂效应带来差值信息，然后对量测信息进行补偿，从而修正杆臂效应带来的误差，这种方法需要预先得知杆臂的长度。李蓓[36]对两种杆臂效应的补偿方法进行了比较，得出了计算补偿法精度较高的结论。

针对大方位失准角杆臂长度未知的情况下杆臂效应的补偿问题，高伟[37]提出用滤波器估计杆臂长度，再采用计算补偿法进行补偿，在江上船载实验得到的结果表明该方法无论是传递对准精度还是对准时间上都优于采用低通滤波器的滤波补偿方法。刘锡祥[38-39]提出构建滤波算法以解决大杆臂条件下杆臂长度的不确定性问题，仿真结果表明可以精确估计杆臂长度，有效实现对杆臂效应误差的补偿。

4.3时延误差与补偿

传递对准过程中，由于主子惯导间存在信息传输延迟和启动时间点具有随机性，会造成信息在时间上的不统一。对于时延误差，一种处理方法是将时间延迟分解为一项常值延迟和一项随机延迟，在传递对准滤波器中对其进行估计和补偿，波音公司在处理JDAM导航系统中的时间延迟时就是采用的这种方法[40]；陈刚[41]和陈雨[42]也采用这种方法研究了对时延误差的补偿。夏家和[43]提出预先存储子惯导数据，等待主惯导数据到达后再进行滤波估计和更新的方法。徐林[44]对3种时延误差的补偿方法进行了比较，分析了3种方法的优势和不足。

5传递对准的滤波算法

传递对准的数学模型本质上描述的是观测量与失准角等误差参数的传播规律之间的联系，滤波算法的作用就是利用已知的观测量对未知的误差参数进行估计。在滤波算法设计时，主要考虑是算法的精度、鲁棒性和实时性。

对于小角度情况下传统的线性传递对准模型，卡尔曼滤波器(KF)和扩展卡尔曼滤波器(EKF)得到了广泛的应用。在理想的情况下KF和EKF可以获得不错的滤波精度，但是这是建立在一系列前提下的：系统是线性系统、系统噪声和量测噪声是高斯白噪声且统计特性已知等。在不满足这些条件的情况下，滤波算法的精度会下降，甚至出现发散。另一方面，算法在高维系统下计算量会很大。为此，学者们提出了很多改进措施如降维算法[45]、在滤波器设计中引入自适应方法和联邦滤波思想[9,46]等。

低精度的惯导器件和初始失准角的增大都会导致系统非线性程度的增强。对于非线性滤波问题，EKF是通过对当前状态的非线性系统进行近似泰勒展开，同时只保留一阶精度，面对强非线性系统时，精度较低，同时还容易导致发散。与扩展卡尔曼滤波相比，无迹卡尔曼滤波滤波(UKF)和容积卡尔曼滤波(CKF)均无需对非线性模型进行线性化处理，更适于处理非线性滤波问题，目前，在传递对准的研究中，UKF提出的较早，得到了广泛的应用[6-7,37]；CKF 2009年由Arasaratnam和Heykin提出[47]，由于在理论分析上在高维度情况下的稳定性和精度要优于UKF[48]，也得到了不少关注[8,35]。

除了卡尔曼滤波,H∞滤波[49-51]、联邦滤波[49,52]、粒子滤波[53]也均在被传递对准研究中被应用。在实时性方面具有优势的一些智能滤波算法如神经网络[54]、最小二乘支持向量机(LS-SVM)[55]也被应用在传递对准滤波器的设计中。

6结论

传递对准是采用惯性制导的精确制导武器中的关键技术，本研究从系统模型、匹配方法、可观测性、误差补偿和滤波方法几个方面简要总结了近年来传递对准技术的相关理论与发展。

从当前的发展来看，传递对准技术存在如下发展趋势：①传递对准所利用的信息多样化，除了主子惯导提供的信息外，GPS、雷达等设备提供的信息也可用于辅助传递对准。②随着传递对准中新的模型、误差补偿技术和滤波器技术的发展，传递对准的性能将会不断提高。③可观测度的相关研究将会继续深入，进而更好地指导传递对准滤波器的设计。

参考文献：

[1]CHUNG D Y,LEE J G.Comparison of SDINS in-flight alignment using equivalent error models[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(3):1046-1054.

[2]徐林,李世玲,曲新芬.惯性导航系统传递对准综述[J].信息与电子工程,2010,8(6):633-640.

[3]ROGERS R M.Low dynamic IMU alignment[C]//IEEE Position Location and Navigation Symposium.Palm Springs,CA:IEEE,1998:272-279.

[4]KAIN J E,CLOUTIER J R.Rapid transfer alignment for tactical weapon applications[C]//AIAA Guidance,Navigation and Control Conference.Boston,1989:1290-1300.

[5]陈凯,鲁浩,闫杰.快速传递对准方程与传递对准方程的一致性研究[J].西北工业大学学报.2008,26(3):326-330.

[6]熊芝兰,郝燕玲,孙枫.基于四元数的惯导系统快速匹配对准算法[J].哈尔滨工程大学学报,2008,29(1):28-34.

[7]周卫东,吉宇人,乔向伟.四元数扩维无迹卡尔曼滤波算法及其在大失准角快速传递对准中的应用[J].控制理论与应用,2011,28(11):1583-1588.

[8]陈雨,赵剡,李群生.基于QCKF的大失准角快速传递对准[J].北京航空航天大学学报,2013,39(12):1624-1628.

[9]CHEN YU,ZHAO YAN.New rapid transfer alignment method for SINS of airborne weapon systems[J].Journal of Systems Engineering and Electronics,2014,25(2):281-287.

[10]FARRELL,JAMES L.Transfer Alignment for Precision Point Application [C]// NAECON Proceedings of IEEE Proc Natl Aerosp Electron Conference.Dayton,Ohio:IEEE,1979:132-137.

[11]YAMAMOTO G H,BROWN J I.Design,Simulation and Evaluation of the Kalman Filter Used to Align the SRAM Missile[R].AIAA71-948:453-461.

[12]ROSS C C,EIBERT T F.A transfer alignment algorithm study based on actual flight test data from a tactical air-to-ground weapon launch[R].IEEE Position Location and Navigation Symposium,1994:431-438.

[13]张红梅，邓正隆.一种新的惯性导航初始对准滤波方法[J].中国惯性技术学报，2005,13(1):1-4.

[14]林敏敏,房建成,高国江.一种有效的空-空导弹捷联惯导系统快速精确传递对准方法[J].中国惯性技术学报,2001,9(3):24-29.

[15]陈凯,鲁浩,闫杰.传递对准姿态匹配的优化算法[J].航空学报,2008,29(4):981-987.

[16]管叙军,王新龙.捷联惯导动基座传递对准匹配方法[J].航空兵器,2014.2:3-9.

[17]SHORTELLE K J,GRAHAM W R,RABOUM C.F-16 flight tests of a rapid transfer alignment procedure[R]// IEEE Position Location and Navigation Symposium.[S.l.]:[s.n.],1998:379-386.

[18]王司,邓正隆.机载导弹空中二次快速传递对准方法研究[J].航空学报,2005,26(4):486-489.

[19]王金林,陈明,郭创.基于“姿态矩阵”量测的机载导弹传递对准技术[J].火力与指挥制,2005,30(4):55-58.

[20]WENDEL J,METZGER K,TROMMER G F.Rapid transfer alignment in the presence of time correlated measurement and system noise[C]//AIAA Guidance,Navigation and Control Conference.Province,Rhode Island:AIAA,2004:307-318.

[21]陈凯,鲁浩,赵刚,等.传递对准姿态匹配算法的统一性[J].中国惯性技术学报,2008,16(2):127-131.

[22]刘镇波,李四海,王珏,等.相对姿态匹配传递对准方法[J].系统工程与电子技术,2014:36(8):1619-1625.

[23]GOSHEN-MESKIN D,BAR-ITZHACK I Y.Observability analysis of piece-wise costant system,Part I:Theory[J].IEEE Transactions on Aerospace and Electronic Systems,1992,28(4):1056-1067.

[24]GOSHEN-MESKIN D,BAR-ITZHACK I Y.Observability analysis of piece-wise costant system,Part II:Application to inertial navigation in-flight alignment[J].IEEE Transactions on Aerospace and Electronic Systems,1992,28(4):1068-1075.

[25]HAM F,EMBROWN T G.Observability,eigenvalues,and Kalman filtering[J].IEEE Transactions on Aerospace and Electronic Systems,1983,19(2):269-283.

[26]程向红,万德钧,仲巡.捷联惯导系统的可观测性和可观测度研究[J].东南大学学报,1997,27(6):6-11.

[27]马艳红,胡军.基于SVD理论的可观测度分析方法的几个反例[J].中国惯性技术学报,2008,16(4):448-452.

[28]杨晓霞,阴玉梅.可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J].中国惯性技术学报,2012,20(4):406-409.

[29]孔星炜,董景新,吉庆昌,等.一种基于PWCS的惯导系统可观测度分析方法[J].中国惯性技术学报,2011,19(6):631-636.

[30]陈雨,赵剡,李群生.一种可观测度分析方法在传递对准中的应用[J].中国惯性技术学报,2013,21(4):467-471.

[31]SPALDING K,MISSOURI S L.An efficient rapid transfer alignment filter[C]//Proceedings of AIAA Guidance,Navigation and Control conference.Hilton Head Island:AIAA,1992:1276-1286.

[32] LIM Y C,LYOU J.An error compensation method for transfer alignment[C].Proceedings of IEEE Conference on Electrical and Electronic Technology,2001(2):850-855.

[33]YANG CHUN,LIN CHING-FANG,TARRANT D.Transfer alignment design and evaluation[R].AIAA-93-3892.

[34]刘锡祥，徐晓苏，王立辉.基于H∞滤波的主/子惯导组合中挠曲变形补偿算法[J].中国惯性技术学报,2012,20(1):74-78.

[35]王跃钢,杨家胜,文超斌.捷联惯导大失准角下传递对准的鲁棒算法[J].现代防御技术,2013,41(6):32-37.

[36]李蓓,高伟,王嘉男,等.传递对准中杆臂效应误差的补偿研究[J].弹箭与制导学报,2008,28(6):49-52.

[37]高伟,张亚,孙骞,等.传递对准中杆臂效应的误差分析与补偿[J].仪器仪表学报,2013,34(3):559-565.

[38]刘锡祥,徐晓苏.杆臂效应补偿中H∞滤波器的应用与设计[J].东南大学学报,2009,39(6):1142-1145.

[39]刘锡祥,徐晓苏.大杆臂条件下传递对准算法的设计与仿真[J].系统仿真学报,2011,23(5):1051-1053,1058.

[40]KLOTZ H A JR,DERBAK C B.GPS-aided navigation and unaided navigation on the Joint Direct Attack munition[R]//IEEE Position Location and Navigation Symposium.New York:IEEE,1998:412-419.

[41]陈刚,周超,刘红光.时间延迟对姿态角匹配传递对准的影响[J].中国惯性技术学报,2014,22(2):172-176.

[42]陈雨,赵剡,李群生,等.快速传递对准中主惯导信息之后补偿方法[J].中国惯性技术学报,2013,21(5):576-580.

[43]夏家和,秦永元,赵长山.传递对准中主惯导参考信息滞后处理方法研究[J].兵工学报,2009,30(3):342-345.

[44]徐林,李世玲,曲新芬.三种传递对准延时误差补偿方法的比较研究[J].兵工自动化,2011,30(2):22-25.

[45]纪志农,李海军,李新纯,等.捷联惯导系统传递对准误差模型降阶分析[J].中国惯性技术学报,2009,17(4):403-407.

[46]张涛,徐晓苏.基于自适应联邦滤波的传递对准算法[J].中国惯性技术学报,2007,15(5):512-516.

[47]ARASARATNAM I,HAYKIN S.Cubature Kalman Filters [J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[48]孙枫,唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较[J].控制与决策,2013,28(2):303-321.

[49]高社生,姜微微,宋飞彪.奇异值分解H∞联邦滤波及其在传递对准中的应用[J].中国惯性技术学报,2011,19(5):521-525.

[50]宋丽君,秦永元,严恭敏.H∞次优滤波在速度姿态匹配传递对准中的应用[J].传感技术学报,2012,25(1):49-52.

[51]陈雨,赵剡,李群生.一种混合H∞/H2滤波的传递对准算法[J].系统工程与电子技术,2013,35(11):2390-2395.

[52]王勇军,徐景硕,高扬.舰载机惯导快速传递对准的联邦滤波器设计[J].压电与声光,2014,36(1):42-46.

[53]郭子伟,缪玲娟,赵洪松,等.一种改进的类高斯和粒子滤波在大失准角传递对准中的应用[J].航空学报,2013,34(1):164-172.

[54]李玉峰,张宗麟,张冬冬.基于Hopfield网络的空-空导弹传递对准研究[J].弹箭与制导学报,2002,22(4):105-108.

[55]于亚静,李擎.LS-SVM在车载SINS大失准角传递的对准上的应用[J].传感器与微系统,2013,31(1):145-152.

(责任编辑杨继森)

Development of Transfer Alignment for Inertial Navigation Systems

SONG Jia-yu, YANG Li-ming, LI Dong-jie

(Institute of Electronic Engineering, China Academy of Engineering Physics, Mianyang 621000, China)

Abstract:As inertial navigation is completely autonomous, highly covert and has a high data frequency, and it is widely used in military technology. Transfer alignment is the key technology of inertial navigation and it’s important to assure the accuracy of inertial navigation system used in guided munitions. The developing status of transfer alignment was introduced by following aspects: system model, matching method, observing, compensation method and filter design. The research progress of transfer alignment technology in recent years was summarized. The possible developments in the future were discussed.

Key words:inertial navigation; transfer alignment; matching method; observability

文章编号：1006-0707(2016)02-0139-05

中图分类号：TJ765.3

文献标识码：A

doi:10.11809/scbgxb2016.02.034

作者简介：宋嘉钰(1988—)，男，硕士研究生，主要从事惯性导航传递对准技术研究。

收稿日期：2015-08-25；修回日期：2015-09-10

本文引用格式：宋嘉钰，杨黎明，李东杰.惯性导航传递对准技术发展现状与趋势[J].兵器装备工程学报，2016(2):139-143.

【信息科学与控制工程】