船用核动力一回路系统使用可用度仿真

王　建，陈力生，李东兴，张永发，李少帅

(1.海军工程大学 核能科学与工程系，武汉　430033; 2. 92730部队，海南 三亚　572000)



船用核动力一回路系统使用可用度仿真

王建1，陈力生1，李东兴2，张永发1，李少帅1

(1.海军工程大学 核能科学与工程系，武汉430033; 2. 92730部队，海南 三亚572000)

摘 要：船用核动力一回路系统的可用性是长期以来备受关注的重要问题，由于一回路系统有复杂可修的特点，其可靠性框图并联分支中有两个以上单元串联这种局部结构尤为常见，以往用正常、维修、待用3种使用状态不足以描述其实际的使用情况，充分考虑系统各单元的6种使用状态，基于最小路集判断各单元的状态转移，采用蒙特卡罗数值仿真方法，克服常规解析方法求解困难的弊端，求得了系统的多项可用性指标;仿真方法对复杂可修系统具有通用性，仿真结果可以为装备的运行与使用管理提供参考。

关键词：核动力一回路；多个使用状态；最小路集；蒙特卡罗；使用可用度仿真；复杂可修系统

Citation format:WANG Jian, CHEN Li-sheng, LI Dong-xing,et al.Operational Availability Simulation for Primary Loop of Marine Nuclear Power Plants[J].Journal of Ordnance Equipment Engineering,2016(2):37-40.

使用可用度可用于描述舰船系统或设备能够投入使用的概率，是装备战备完好性的重要参数之一[1]，使用可用度综合考虑了与使用相关的诸多因素(如维修政策、系统允许停用时间、保障延误时间等)，直接关系到舰船连续运行的能力[2]，对其定量计算对装备的运行与使用管理具有重要意义。

现有对舰船系统使用可用度的建模与计算方法中，多数为了建模及编程的方便，考虑单元存在3种使用状态[3-5]，即正常、维修、待用3种状态，这种简化可以满足简单串、并联系统的使用可用度的计算需求，但对于稍复杂的系统而言，这样的考虑无法反映装备的实际使用状况。例如图1所示系统可靠性框图，单元1的故障会导致单元2转为待用状态，在单元1维修期间，若单元3故障且维修工不足，则3的状态转为待修，若单元5也故障，单元3修好后则转为修好待用状态，显然“正常、维修、待用”3种状态不足以反映实际情况。对于运行期间的舰船系统而言，在使用时会存在多种故障模式，设备故障后在一定条件下可修，其组成设备是否可修与一回路特殊环境的维修条件有关，为了真实的反映系统的实际使用状况，减少计算误差，本文充分考虑”正常工作、正在维修、等待修理、正常待用、维修待用、故障后不可修”6种使用状态，并采用蒙特卡罗方法，可以求的系统的各种可用性指标。

图1　系统可靠性框图

基于蒙特卡罗思想的复杂可修系统的可靠性或可用度仿真中，主体思想有几种，分别是基于故障树最小割集、故障树结构函数、最小路集的思想。基于故障树最小割集的可靠性或可用性数值仿真[6]虽然能较好的解决不可修系统的可靠性计算问题，但是考虑可修时，不能清楚地反映各事件之间的逻辑关系，尤其当最小割集之间相交化程度高时，会给数值仿真带来较大麻烦。基于故障树结构函数[7]的可靠性数值仿真方法可以将大型复杂可维修系统的动态仿真过程分解为一系列静态过程，减少计算量，但是当系统过于庞大时，故障树结构函数的处理也过于繁琐，很难实现。基于最小路集的可用性数值仿真[8]可以弥补基于最小割集思路的弊端，较好的反映系统中各单元的逻辑关系，可判断一个单元状态的变化对其他单元的产生的影响。本文采取基于最小路集的思路进行数值仿真。

1仿真思路

给定运行时间，根据系统中各单元的寿命分布，结合蒙特卡罗思想，随机抽样获得各单元的寿命，寿命最短的单元先故障并主动发生状态转移，同一最小路集中其他受影响单元的状态发生被动转移，根据状态转移的规则判断各单元及系统转移后的状态，并更新抽样时间向量(例如单元状态转移后若处于正在维修，则随机抽取产生维修时间)，每次状态转移记录相关数据，当仿真时间到达给定运行时间或者系统故障后不可修时，结束单次仿真，满足计算精度所需的仿真次数时，统计并计算系统使用可用度相关参数。图2为单次仿真的流程图。

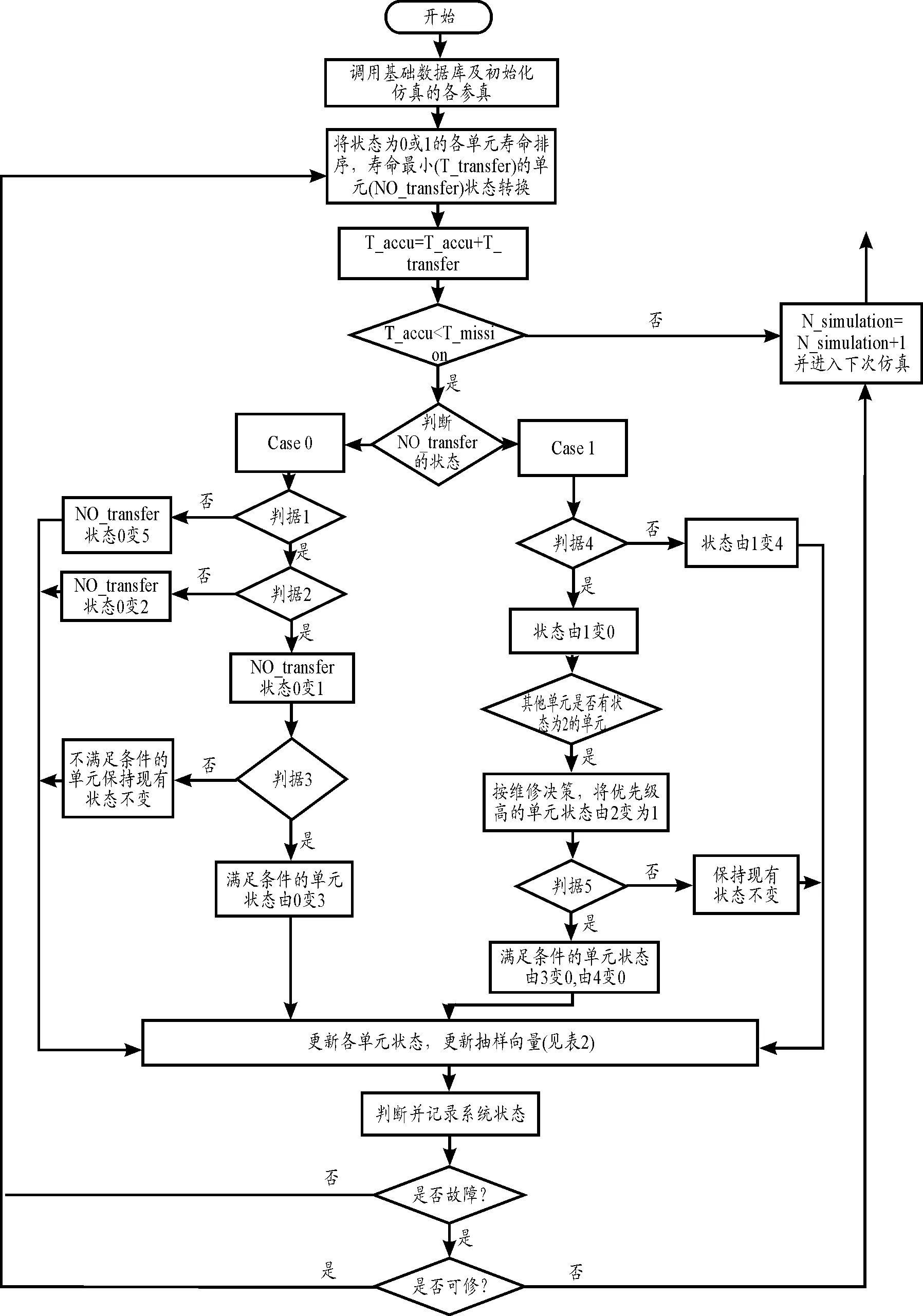
图2　单次仿真的流程

1.1基本假设

(1)系统各单元采用先故障先修理的维修策略；

(2)系统各单元修复如新；

(3)处于“正常待用”和“修好待用”状态的设备不发生故障；

(4)维修时间服从指数分布。

1.2对单元寿命和修复时间进行抽样

设单元的寿命函数为F(t)，寿命抽样值为t=F-1(η)其中η为(0,1)区间随机数，维修时间抽样同理，几种常见的分布抽样公式参见文献[9]，调用的基础数据包括各单元寿命和修复时间的数据文件，以及最小路集的存放文件。

1.3判断各单元状态转移的状况

找出状态为正常工作或正在维修(状态为0或1)的单元，将这些单元对应的抽样时间进行从小到大排序，排名第一的单元标记为单元NO_transfer，其状态发生主动转移，并会导致其他单元的状态被动转移，判断分为两种情况：

(1)当单元NO_transfer的状态为正常工作(状态为0)时：

判据1单元NO_transfer是否可修。如果不可修，其状态由正常工作转化为故障不可修(状态0→5)。

判据2单元NO_transfer可修的前提下，维修工的数量是否大于0。如果大于0，其状态由正常状态转为正在维修(状态0→1)。如果等于0，其状态由正常状态转为等待维修(状态0→2)。

判据3是否存在这样的单元，即除了NO_transfer以外的其他单元不包含在连通的最小路集，而只包含在单元NO_transferd的最小路集中。如果存在则这部分单元由“正常工作”转向“正常待用”状态(状态0→3)。

(2)当单元NO_transfer的状态为正在维修(状态为1)时：

判据4单元NO_transfer所在的全部最小路集中是否都存在至少一个状态为“正在维修”或“等待维修”或“故障后不可修”的单元。如果是，则单元NO_transfer由“正在修理”转为“修理待用”状态(状态1→4)。

判据5如果单元NO_transfer所在的任意一个最小路集中，所有其他单元的状态为“正常工作”、“正常待用”或“修理待用”，则单元NO_transfer的状态由“正在维修”转为“正常工作”(状态1→0)。

此时还要将其他单元处于“正常待用”或“修理待用”状态转移为“正常工作”的状态(状态3→0，4→0)。

1.4时间抽样向量的更新方法

时间抽样向量的更新方法见表1。

表1　各单元时间抽样向量的更新方法

1.5仿真统计结果

系统使用可用度：

A0=系统可用时间/(系统可用时间+系统不可用时间)

运行成功率：

当运行期间系统总不可用时间小于最大允许停机时间时认为连续运行成功。

R0=运行成功次数/仿真总次数平均首次故障时间：

仿真时不设定运行时间，当系统第一次达到故障时，记录仿真的时间，累计总时间求均值即为平均首次故障时间。

2计算实例

2.1数据给出

以装置连续长时运行为例，假定反应堆一直运行在50%功率以下，系统允许最大停机时间72 h。图3为反应堆一回路相关系统的可靠性框图，一回路系统相关的可靠性、维修性参数见表3。表3中数据是在借鉴了WASH-1400以及文献[10]基础上，经过一定处理给出，其中可修概率为单元出现可维修故障模式的概率，控制线路故障能在不停堆下直接维修，而阀门故障、电机故障和密封故障等必须在停堆状态下维修，并且在停机后需要等待放射性减少到一定程度再进入现场维修，运行期间蒸汽发生器传热管破裂等故障模式为不可修故障。

2.2计算结果

为满足计算精度，仿真进行10 000次。对于服从威布尔分布的单元，无法给出精确的形状参数β，改变β的大小(1~3.0)，得到运行成功率：0.711 9≤R0≤0.969 8，系统使用可用度：0.843 0≤A0≤0.991 4，系统平均首次故障前时间为 6.716 8×103h，系统平均可修复概率为0.753 9。

图3　需求功率在半功率以下的反应堆及

单元序号服从寿命分布特征寿命(或寿命中值)/h可修概率修复时间中值/h1威布尔1×1040.90.22~5威布尔3.3×1030.60.26~9威布尔3.3×1040.60.210~11正态1.6×1040—12威布尔6.7×1030.60.213威布尔6.7×1030.60.214~15指数3.3×1040.60.216~17威布尔3.3×1030.91018~19威布尔3.3×1030.91020威布尔6.7×1030.9521~22威布尔3.3×1030.91023威布尔6.7×1030.95

在β=1.8时，各单元故障次数以及修复次数如图4，维修工数对使用可用度的影响可见图5。

改变系统的使用时间，可得到不同形状参数β下系统运行成功率R0、使用可用度A0随使用时间的变化趋势，如图6、图7所示。

图4　每个单元的故障与修复次数

图5　A0随维修工数量变化曲线

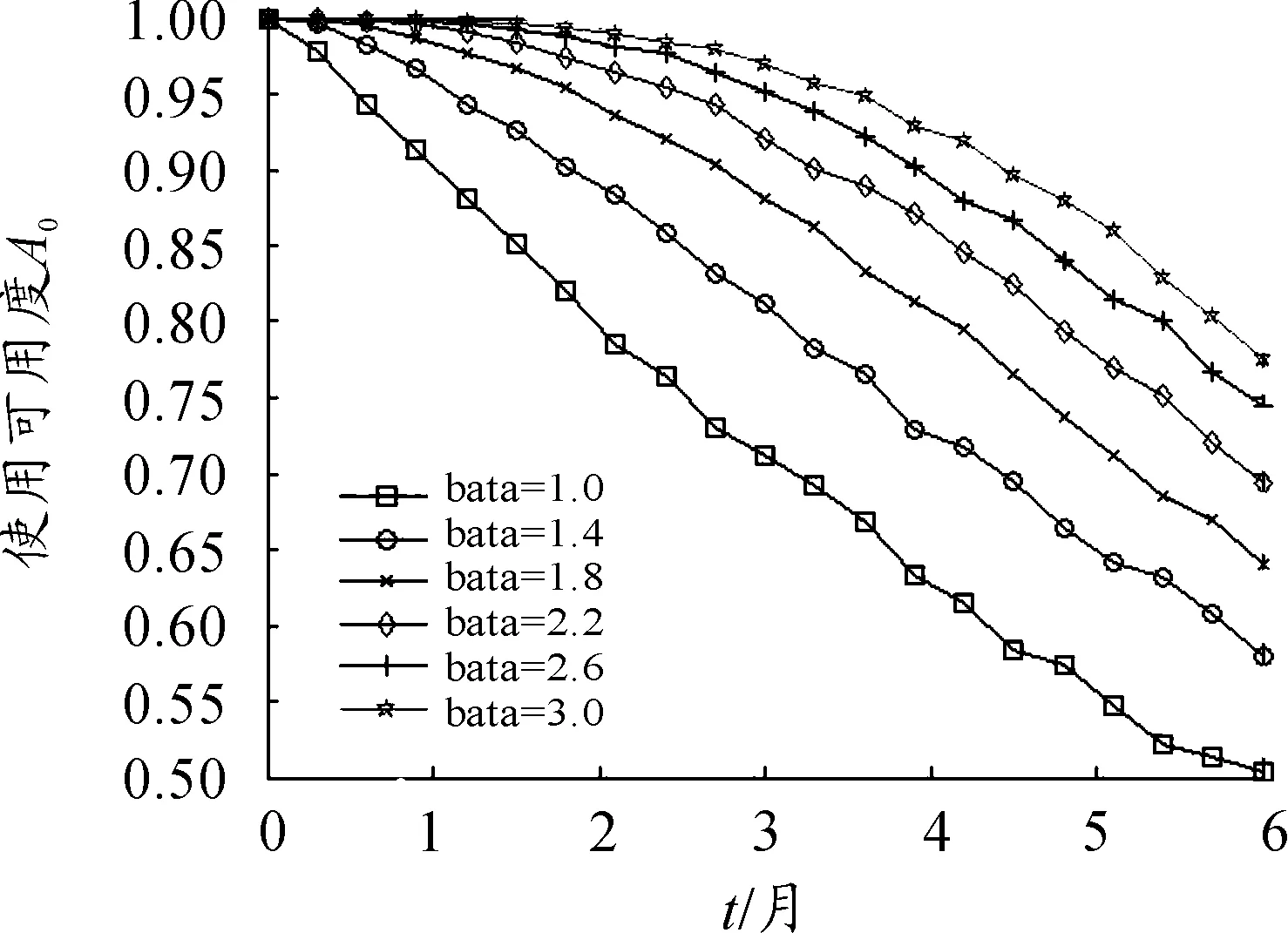
图6　不同β下R0随使用时间变化曲线

图7　不同β下A0随使用时间变化曲线

2.3结果分析

从仿真结果可看出在运行时间内，一回路系统具有较高的使用可用度和运行成功率，运行完成情况良好。在10 000次仿真中，单元2和单元22故障次数最多，平均一次运行故障次数为0.39次，故障频率较低。维修工数为0时，系统相当于完全不可修，此时系统使用可用度最低为0.825 8，当维修工数大于1时，增加维修工对使用可用度影响很小，原因在于单元故障频率低，抢修时间短，基本不存在多个单元同时维修的情况。

2.4结论

每次连续运行前，把系统调试到所有单元都正常，连续运行期间不希望发生故障，所以特别关心平均首次故障前时间、运行成功率、系统使用可用度等参数，同时，每个单元故障次数对其备件数目的估算以及系统维修策略的选定具有重大意义，通过本文仿真的思路可以得到多项可用性相关的指标。程序具有通用性，只需要给出各单元可靠性维修性保障性参数和最小路集，即可计算可用性相关的参数，这是常规解析方法难以实现的。计算结果对装备的维修和保障有一定的参考价值。

参考文献：

[1]甘茂治,康建设,高崎.军用装备维修工程学[M].北京:国防工业出版社,1999.

[2]李能鹏,马丽萍.舰船系统有效可用度内涵分析及应用探讨[J].舰船科学技术,2011(6):130-133.

[3]徐廷学,魏勇.基于备件库存的舰炮使用可用度建模与仿真[J].装备环境工程,2010(5):132-137.

[4]王进才.军用直升机使用可用度仿真研究[J].电子产品可靠性与环境试验,2010(4):1-5.

[5]王蕴,王乃超,马麟,等.考虑备件约束的多部件串联系统使用可用度计算方法[J].航空学报,2015,36(4):1195-1201.

[6]易宏,袁远.以最小割集为基础的可靠性数值仿真[J].上海交通大学学报,1997(9):119-123.

[7]褚卫明,易宏,张裕芳.基于故障树结构函数的可靠性仿真[J].武汉理工大学学报,2004(10):80-82.

[8]金星，洪延姬.蒙特卡罗方法在系统可靠性中的应用[M].北京：国防工业出版社，2012.

[9]杨为民，盛一兴.系统可靠性数字仿真[M].北京：北京航天航空大学出版社，1990．

[10]阎凤文.设备故障和人误数据分析评价方法[M].北京：原子能出版社，1988.

(责任编辑周江川)

Operational Availability Simulation for Primary Loo of Marine Nuclear Power Plants

WANG Jian1， CHEN Li-sheng1, LI Dong-xing2, ZHANG Yong-fa1, LI Shao-shuai1

(1.Power Engineering College, Naval University of Engineering, Wuhan 430033, China;2.The No. 92730thTroop of PLA, Sanya 572000, China)

Abstract:The availability of marine nuclear power plants (MNPP) primary loop system is a persistently concerned problem. It can’t describe the actual situation of using with the usual solution consisting three using situations: normal, maintaining and standby because the primary loop system is complex maintainable and it is a common local structure that more than one series structures are mixed in the parallel branch. Considering 6 working conditions, based on the thought judgment system of minimal path sets, the Monte-Carlo numerical simulation method was combined to overcome the disadvantages of conventional analytical method. Taking the primary circuit system of nuclear power plant for example, the various availability indexes were obtained. The simulation method is widely applicable and the simulation results can be used to provide the reference for equipment operation and management.

Key words:primary circuit system; multi operational condition; minimal path set; Monter-Carlo; operational availability simulation; complex repairable system

文章编号：1006-0707(2016)02-0037-05

中图分类号：TJ247

文献标识码：A

doi:10.11809/scbgxb2016.02.010

作者简介：王建(1991—)，男，硕士研究生，主要从事核科学与技术研究。

收稿日期：2015-05-27；修回日期：2015-07-15

本文引用格式：王建，陈力生，李东兴，等.船用核动力一回路系统使用可用度仿真[J].兵器装备工程学报，2016(2):37-40.

【装备理论与装备技术】