基于时域能量划分和PSO-SVM的发动机故障诊断*
2016-04-11胡志勇牛家骅郭丽娜马继昌
胡志勇,牛家骅,郭丽娜,马继昌
(内蒙古工业大学,呼和浩特 010051)
2016014
基于时域能量划分和PSO-SVM的发动机故障诊断*
胡志勇,牛家骅,郭丽娜,马继昌
(内蒙古工业大学,呼和浩特 010051)
针对发动机缸盖振动信号激励源的时序性,提出了一种基于时域能量划分和粒子群优化-支持向量机算法(PSO-SVM)的发动机故障诊断方法。将振动信号按曲轴转角进行时域能量划分并将各段时域信号能量组成的向量作为故障分类的特征向量,应用不同优化技术的支持向量机(SVM)算法对发动机配气机构故障进行识别。诊断结果表明:时域能量划分结合PSO-SVM在小样本的情况下,能够对既定机型的配气机构和点火系常见故障进行识别。
发动机;故障诊断;振动信号;时域特征向量;支持向量机
前言
发动机是汽车的动力源,其工作条件恶劣、故障率高。而在使用中,气门间隙异常和个别气缸丢火是发动机最常见的故障。发动机气门间隙异常将对发动机的进排气效果、运行平稳性和排放性能等指标产生直接影响;而发动机点火异常将直接使发动机丧失工作能力。因此,在发动机不解体条件下监测发动机工作状况,在故障出现时确定气门间隙和点火系故障的位置,具有一定的应用价值[1-2]。
故障诊断的实质是对故障模式的识别过程,包括特征提取和状态识别两个关键环节。发动机缸盖表面振动信号测量时发动机无须解体,方便快捷,所含振动、冲击和噪声等信号信息丰富,可以实时地反映发动机的工作状态[3-4]。
本文中通过分析发动机缸盖振动信号激励源的时序性和发动机工作异常时缸盖表面振动信号的变化,在发动机不解体的情况下,对采集的振动信号按曲轴转角进行时域划分并计算各段能量,将各段能量作为测试集和训练集的特征向量,运用故障分类器对故障进行分类识别。
1 发动机缸盖振动特性
发动机振动信号是由一系列频率和幅值差别较大的瞬态响应所组成,情况比较复杂,而最具影响的是燃烧引起的直接激振力和气门开启、落座产生的间接激振力。由于发动机各部件按一定周期工作,振动信号先后有序,若发动机出现某种故障,发动机一个工作周期内的激振力的响应信号在时域上的幅值和相位等都将发生改变,据此可以获取特征参数并进行故障诊断[5-6]。
图1为实验测得的DA462型汽油发动机缸盖表面第1缸振动信号波形图,其实验条件是发动机转速为1 750r/min,正常气门间隙(0.15mm),图中A点为第1缸排气门落座冲击;B点为第2缸燃烧激励压力响应;C点为第1缸进气门落座冲击;D点为第1缸燃烧激励压力响应;E点为第1缸排气门开启冲击;F点为第3缸燃烧激励压力响应;G点为第1缸进气门开启冲击;H点为第4缸燃烧激励压力响应。当发动机出现某种故障时,图中相应的波形在时间轴上的位置和振幅就会发生改变,这为故障的分析和识别提供了依据。
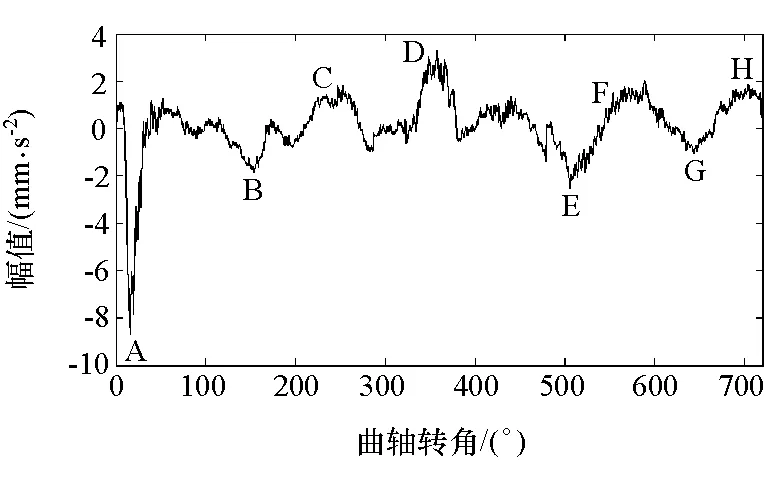
图1 发动机缸盖表面振动信号波形
2 时域特征向量的提取
设采集的振动信号为x(t),则其在t1到t2时间段的能量为
(1)
这是最理想的状态,而由加速度传感器采集得到的发动机时域振动信号为离散值,设其最小采样间隔Δt=1/f,其时域能量为
(2)
式中:n=(t2-t1)/Δt;x(t1+kΔt)为采集的信号在各个离散点的幅值。在发动机一个工作周期内,按照曲轴转角把振动信号划分为n段,设各段有m个能量幅值,各段能量幅值离散的集合为{x1,x2,…,xj,…,xm},则第i段能量幅值和为
(3)
式中:i=1,2,…,n;f为采样频率;xj为振动信号离散点的幅值。
再对Ei进行归一化,设Es=E1+E2+…+En,则特征向量为
E=[E1/Es,E2/Es,…,En/Es]
(4)
3 支持向量机
支持向量机(SVM)是一种针对小样本、以统计学习理论为基础的学习算法,可用于模式分类和非线性回归。其主要思想是建立一个分类超平面作为决策曲面,使得正、反例的边缘间隔最大化[7]。
支持向量机包括二分类支持向量机和多分类支持向量机。SVM本质上是一种二值分类器,故二分类支持向量机为SVM的雏形。多分类支持向量机主要针对多分类问题,目前的主要方法有两类:一类是直接法,直接在目标函数上进行修改,这种方法计算复杂度高,实现起来比较困难;另一类为间接法,主要是通过组合多个二分类器来实现,常见的方法有1对1算法、1对多算法和DAGSVM算法[8]。
3.1 二分类支持向量机
(1) 线性可分的二分类问题
线性可分的二分类问题是指原数据可以用一条直线或一个超平面划分开,具体形式如下。
假设有n个d维样本数据集为
{xi,yi},i=1,2,…,n,xi∈Rd,yi∈{+1,-1}
设分类超平面为(w·x)+b=0。其中x是d维向量,为使各数据点对分类超平面的几何间隔最大,其优化问题表达为求解式(5)方程组:
(5)
据此求出最优解α*=(α1*,…,αn*)T,并选取α*的一个正分量αj*,计算超平面参数:

(6)
构造决策函数:
(7)
设测试集合为{tj,pj},j=1,2,…,k,则用最优分类超平面预测出的测试集的标签为
(8)
比较tjlabel与pj,若相符说明分类正确,若不一致则说明分类错误。
(2) 线性不可分的二分类问题
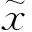
K(xi,xj)=φ(xi)·φ(xj)
(9)
经映射后,样本集变为
选取适当的核函数K(x,x′)和适当的参数C,构造并求解最优化问题:
(10)
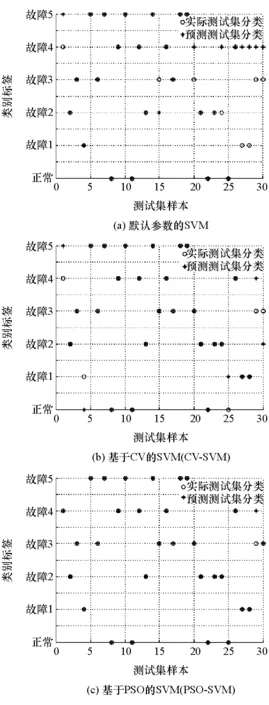
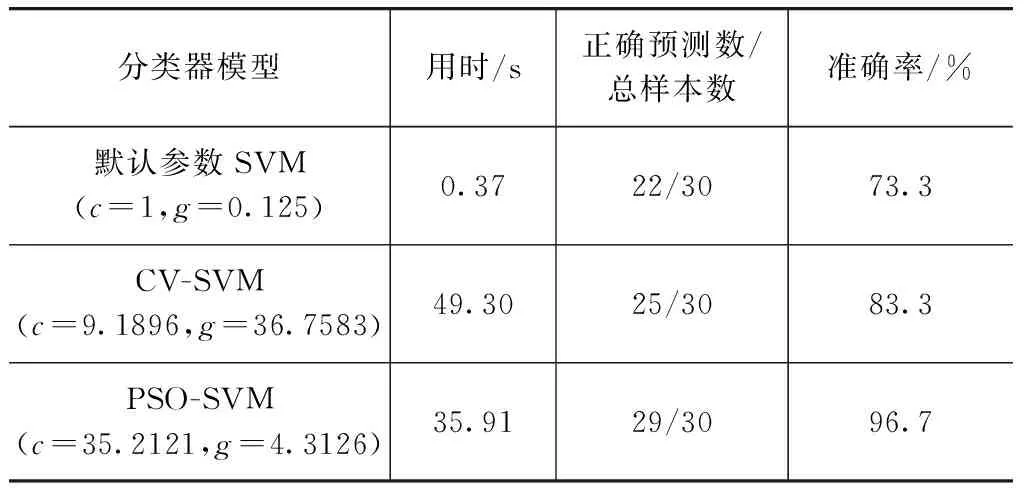
得到最优解α*=(α1*,…,αn*)T,并选取α*的一个正分量0<αj* (11) 构造决策函数: (12) 此时,若有d维输入向量x0,则可以依据上述过程对x0进行分类。 3.2 支持向量机参数寻优算法 在支持向量机发展过程中,如何提高其分类精度和运算速度是支持向量机改进领域的热点之一。近年来国内研究人员相继提出了决策树支持向量机(DT-SVM)、SVM-DL技术、基于遗传算法的支持向量机(GA-SVM)和基于遗传算法决策树的支持向量机(GADT-SVM)[9-11]等,虽然对此做出了一定改进,但也存在着结构冗长和变相增加运算量等问题,导致达不到最佳分类效果。基于上述问题,本文中应用基于粒子群优化算法参数寻优的支持向量机对发动机6种状态进行实际分类。 (1) 交叉寻优算法(CV) 影响SVM分类效果的参数主要有误差惩罚参数c和核函数参数g。若在运行时不对这两个参数进行调整,则默认误差惩罚参数c=1,核函数参数g为属性数目k的倒数(1/k),这些参数并不是分类器达到性能最优时的参数,此时可以令c的变化范围为(-m,m),步长为a,g的变化范围为(-n,n),步长为b,这样c和g可以分别取2m/a和2n/b个值,即有(2m/a)(2n/b)种组合,分别计算各组合正确率,将正确率最高的参数作为最优参数。 (2) 粒子群优化算法(PSO) 粒子群优化算法(PSO)源于鸟群和蜂群等捕食行为的研究。在PSO系统中,每个备选的解被称作一个“粒子”,这些“粒子”在解空间内以某种规律移动,经过若干次迭代后找到最优解[12-13]。在每一次迭代中,粒子通过跟踪本身最优解(pid)和整个微粒群目前的最优解(pgd)来更新自己,更新后公式为 vid=wvid+c1rand()(pid-xid)+c2rand()(pgd-xid) (13) xid=xid+vid (14) 式中:c1和c2为常数;rand()为在某个区间范围内的随机数;w为惯性权值;vid为速度;xid为位置。 将训练集的准确率作为PSO中的适应度函数值,最终得到最优准确率及其对应的c和g值。 粒子群优化算法具有不容易陷入局部最小、算法简单和计算量小的优点,可提高分类器的效率。 图2 振动测试台架示意图 某车用DA462型发动机在中高速区域工作时(1 600~2 000r/min)冲击噪声明显,且有间歇熄火现象,经初步诊断其故障位置是气门组和点火系。因此,搭建了该发动机的振动测试台架(如图2所示)对其进行测试,人为设置了一些故障并进行基于振动信号分析的故障分类识别。 4.1 振动信号的获取 试验利用4507B-005型振动加速度传感器采集振动信号,传感器安装在第1缸对应的气缸盖罩上的气门螺钉处;曲轴位置传感器采用桑塔纳2000GSi型ABS系统的前轮轮速传感器,获得发动机的相位信号。信号采集模块采用LAN-XI3050-A-060型4通道输入模块。为准确定位各缸工作周期,采用EA次级信号夹同步采集第1缸高压点火信号。信号采样频率为16.384kHz。 在测试中,发动机转速为1 750r/min,排气门的正常间隙为0.15mm,设定排气门异常间隙值为0.6mm。设置发动机气缸6种状态:①正常工作状态;②正常气门间隙状态下第1缸丢火(故障1);③第1缸排气门间隙异常(故障2);④第1缸排气门间隙异常且第1缸丢火(故障3);⑤第1,4缸排气门间隙异常(故障4);⑥第1,4缸排气门间隙异常且第1缸丢火(故障5)。 以发动机一个工作周期为采样周期,实验同步采集了第1缸的上止点信号、高压点火信号和缸盖振动信号。每种工况采集15组信号,一共采集90组信号作为训练集A。 把正常工况和故障1~故障5这6种工况编号为1-6,利用Matlab中的函数randperm,按照数字对应的状态描述,设置气门间隙和点火系故障,并在每次设置故障后采集其振动信号。上述过程共进行30次,将30组采样信号组成测试集B。 4.2 振动信号特征向量的提取 发动机一个工作周期为720°CA,信号以活塞运行到第1缸排气上止点为基准进行采集。为了准确区分发动机不同状态下振动激励的变化,将第1缸振动信号的720°CA等分为N=8份,每份90°CA。按式(3)计算不同曲轴转角对应的能量幅值的和,得到特征向量[E1,E2,…,En],按式(4)对得到的特征向量进行归一化处理,得到归一化的特征向量E=[E1/Es,E2/Es,…,En/Es],训练集每种工况可以得到15组归一化的特征向量。从训练集样本数上来看,模拟实验的训练集属于小样本情况。测试集共得到30组归一化的特征向量。图3为训练集A的分维可视化视图,表1为发动机6种状态下第一组特征向量的值。 图3 训练集分维可视化视图 由表1可见,发动机不同工况下的能量特征值有明显的差异,正常状态、故障2和故障4中,E4的值较大,而在故障1、故障3和故障5中,随着第1缸丢火,E4值变小。E4能量段所对应的曲轴转角为活塞位于第1缸压缩行程中点至活塞运行到上止点之间,此区间包含了活塞运行到上止点前某一角度(点火提前角)所对应的点火时刻,所以E4能量段包含了第1缸燃烧激励压力响应的成分。 表1 不同工况下特征向量值 这些在发动机一个工作周期内不同工况下的能量变化,为气门间隙异常和点火系不同故障的状态识别提供了依据。 4.3 分类器的训练和预测结果 将90组训练样本得到的特征向量矩阵A190×8分别输入使用默认参数的SVM、交叉寻优算法的SVM、基于粒子群优化算法的SVM中进行训练,完成训练后,将30组测试样本得到的特征向量矩阵B130×8输入到训练好的神经网络及支持向量机中,预测结果和准确率如图4和表2所示。 图4 分类结果图 图4中,圆圈和星号分别代表不同分类器给出的预测分类结果。 表2 不同分类器的分类指标 由图4和表2可知:使用默认参数时,仅有正常工况和多故障结合的故障5所有预测标签与实际标签相符,对单一故障和两故障结合的情况识别度较低,同时故障3和故障4被误分类的次数较多,说明第1缸丢火和第4缸排气门间隙异常对第1缸缸盖振动信号的影响有相似之处;而在CV-SVM对比组中,分类准确率有所提高;应用PSO-SVM时,仅有1组故障被误分类,其故障识别准确率达到了96.7%;在训练与分类用时上,PSO-SVM虽不及默认参数SVM,但相比传统的CV算法,用时缩短了27%。 综上所述,在小样本情况下,缸盖振动信号时域特征向量结合优化后的SVM能够提高故障识别准确率,而应用粒子群优化算法的SVM,针对传统优化算法对分类模型参数达不到最佳优化效果的问题,有效提高了既定机型下发动机配气机构和点火系常见故障识别的准确率。 在发动机不解体的情况下,采集缸盖表面振动信号,对其按曲轴转角进行时域划分并计算各段能量,将各段能量组成特征向量并形成训练集和测试集,运用不同优化算法下的SVM对故障进行分类预测。实验结果表明,结合时域特征向量提取和POS-SVM可以基本实现对发动机各缸气门间隙故障和失火故障的准确识别。 本文中只针对选定发动机的振动信号进行了基于PSO-SVM方法的故障诊断,但该方法可普及应用于其他发动机的故障诊断。 [1] 周志培.发动机气门间隙异常原因分析及对策[J].柴油机设计与制造,2012,18(1):52-56. [2] SARAVANAN N, SIDDAB-ATTUNI V N S Kumar, RAMACHANDRAN K I. A Comparative Study on Classification of Features by SVM and PSVM Extracted Using Morlet Wavelet for Fault Diagnosis of Spur Bevel Gear Box[J]. Expert Systems with Applications,2008,35(3):1351-1356. [3] 沈志熙,黄席樾,马笑潇.基于EMD和支持向量机的柴油机故障诊断[J].振动、测试与诊断,2010,30(1):19-22. [4] 徐玉秀,杨文平,吕轩,等.基于支持向量机的汽车发动机故障诊断研究[J].振动与冲击,2013,32(8):143-146. [5] 梅卫江,王春林,边金英,等.柴油机气门间隙异常故障振动诊断的试验研究[J].机床与液压,2010,38(17):130-132. [6] 刘建敏,李晓磊,乔新勇,等.基于EMD和STFT柴油机缸盖振动信号时频分析[J].噪声与振动控制,2013(2):133-137. [9] 王金华,黄佐华,刘兵,等.不同点火时刻下天然气掺氢缸内直喷发动机燃烧与排放特性[J].内燃机学报,2006,24(5):394-401. [10] 高有山,李兴虎.电喷柴油发动机汽车经济性模拟计算[J].中国公路学报,2009,22(5):122-126. [11] 高有山,王爱红,高崇仁.天然气蒸汽重整制氢WTT阶段能量消耗及排放分析[J].机械工程学报,2013,49(8):158-164. [12] 高有山,王爱红,高崇仁.原油运输能量消耗及气体排放分析[J].机械工程学报,2012,48(20):147-152. [13] 高有山,李兴虎,蔡凤田.车用燃油生命周期的能量消耗和温室气体排放分析[J].北京航空航天大学报,2009,35(11):1349-1352. [14] GAO Youshan, WANG Aihong. Energy Consumption and Emissions Analysis of Natural Gas Exploitation[C].2011 International Conference on Materials and Products Manufacturing Technology, ICMPMT 2011, Chengdu, China:1525-1529. [15] BARKER L, DAVE R, HALSNS K, et al. Climate Change 2007: Technical Summary[R].Contribution of Working Group III to the Fourth Assessment Report of the Intergovermental Panel on Climate Change,2007. [16] 高有山,李兴虎,黄敏.汽车滑行阻力分析[J].汽车技术,2008(4):30-33. [17] NAM E K, GIANNELLI R. Fuel Consumption Modeling of Conventional and Advanced Technology Vehicles in the Physical Emission Rate Estimator (PERE)[R]. U.S.:EPA,2005. [18] CHRISTOPHER F H, ROUPHAIL N M, ZHAI H, et al. Comparing Real-World Fuel Consumption for Diesel- and Hydrogen-Fueled Transit Buses and Implication for Emissions[J]. Transportation Research.Part D,Transport and Environment,2007,12(4):281-291. [19] WANG M Q. GREET1.5-Transportantation Fuel-Cycle Model Volume 1: Methodology, Development, Use and Results[R]. Center for Transportation Research, Energy Systems Division, Argonne National Laboratory,1999. Engine Fault Diagnosis Based on Time-domainEnergy Division and PSO-SVM Algorithm Hu Zhiyong, Niu Jiahua, Guo Lina & Ma Jichang InnerMongoliaUniversityofTechnology,Hohhot010051 In view of the time sequence of excitation source of engine cylinder head vibration signals, an engine fault diagnosis method based on time-domain energy division technique and particle swarm optimization-support vector machine (PSO-SVM) algorithm is proposed. The vibration signals are divided into time-domain energy according to crankshaft angle, the vectors composed of each time-domain signal energy are taken as the eigenvectors of fault classification, and the faults of engine valve train are identified by SVM algorithm with different optimization techniques. The diagnosis results show that the combination of time-domain energy division with PSO-SVM algorithm can identify the common faults of valve train and ignition system of the specific type of engine under the condition of small sample set. engine; fault diagnosis; vibration signal; time-domain eigenvector; support vector machine *内蒙古自然科学基金(2012MS0704)和内蒙古高校科研基金重点项目(NJZZ11070)资助。 原稿收到日期为2014年7月2日,修改稿收到日期为2014年8月24日。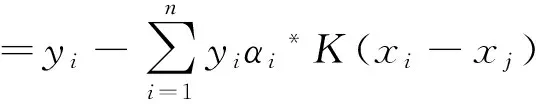
4 发动机故障诊断应用实例


5 结论
