基于蒙特卡洛方法的碳烟生长过程数值模拟*
2016-04-11魏明锐
车 威,魏明锐,李 松
(1.武汉理工大学现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学汽车零部件技术湖北省协同创新中心,武汉 430070; 3.黄淮学院电子科学与工程系,驻马店 463000)
2016003
基于蒙特卡洛方法的碳烟生长过程数值模拟*
车 威1,2,3,魏明锐1,2,李 松1,2
(1.武汉理工大学现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学汽车零部件技术湖北省协同创新中心,武汉 430070; 3.黄淮学院电子科学与工程系,驻马店 463000)
基于弹射凝聚模型构建碳烟颗粒间碰撞的物理模型,采用蒙特卡洛方法构建碳烟颗粒凝聚和表面生长的数学模型并进行数值模拟。引入分形维数、包容半径和凝聚体体积来描述凝聚体分形生长特征,分析表面生长过程对这些参量的影响。对比了不同环境压力和温度对碰撞频率、粒径增长率和分形维数的影响。最后通过枝接过程的模拟,获得了链状凝聚体的形貌特征,并与真实的碳烟照片进行对比,结果表明,枝接过程模拟出的碳烟结构更接近于尾气中真实的链状碳烟形貌。
碳烟颗粒;弹射凝聚;蒙特卡洛方法;分形维数
前言
柴油机工作过程中产生的废气中颗粒物(PM)等对人类健康和环境有极大危害。碳烟颗粒的生成要经历燃料热解、芳香烃形成与生长、碳核形成和颗粒生长4个阶段[1],其间包含有复杂的物理化学过程,涉及从气相分子到固相颗粒的相变过程。目前气相反应的计算可以采用详细的化学反应机理[2],固体颗粒动力学过程主要包括成核后颗粒的碰撞、凝聚、团聚和破碎等过程,这些过程都非常复杂,加之颗粒动力学过程在空间上的非连续性和时间上的非稳定性,难以用确定的数学关系式进行表达[3],目前主要是采用颗粒群平衡方程来描述,该方程是一个积分微分方程,通常没有解析解[4],其求解方法主要有有限元法、有限差分法、矩方法和蒙特卡洛方法等。而针对碳烟颗粒的成核过程,目前在实验上还没有很好的手段,只能采用理论与经验模型模拟颗粒成核。现有的成核机理大致可分为3种[5]:类似富勒烯结构的成核机理、多环芳香烃(PAHs)通过物理凝聚的成核机理和PAHs通过化学环化反应的成核机理。
文献[6]中虽然用矩方法获得了碳烟颗粒动力学演变的相关信息[6],但是没有获得碳烟颗粒的形貌特征。文献[7]中采用分形理论对碳烟的形貌特征进行了分析和模拟,但没有研究表面生长和环境因素对分形维数的影响。文献[8]和文献[9]中采用蒙特卡洛方法进行的计算集中在求解颗粒群平衡方程,包含颗粒的成核、凝并和氧化过程,而本文中则采用蒙特卡洛方法来构建碳烟颗粒凝聚和表面生长的数学模型并进行数值求解。
首先利用分形维数、包容半径和凝聚体体积等参量分析粒子的凝聚特点,其次探究环境压力和环境温度对碰撞频率、粒径增长率和分形维数的影响,最后模拟两种情况下的枝接过程,并与真实碳烟照片进行对比,探讨碳烟颗粒的形成机制。
1 碳烟颗粒动力学理论与建模
本文中不考虑成核前的气相反应过程,假设初始碳核大小相同,并在空间随机产生,然后按照弹射运动形式与其他粒子碰撞,在碰撞过程中考虑表面反应和氧化反应。
1.1 初始粒子与凝聚体碰撞——凝聚过程
粒子的运动形式有布朗运动、弹射运动和受限扩散等,本文中选取弹射运动模式来模拟粒子间碰撞凝聚。
如图1(a)所示,将笛卡尔坐标系原点定义为凝聚中心,在凝聚中心设置一个粒子,定义该粒子为凝聚体,利用蒙特卡洛方法在空间中随机产生一个初始粒子,并以随机方向沿直线弹射运动,与凝聚体之间产生相对运动。若发生碰撞则粘附在一起并作为下次碰撞的凝聚体,如图1(b)所示;若不发生碰撞,初始粒子沿着随机运动方向超出定义边界后消失,然后以相同方式产生下一个初始粒子,这样周而复始,最终完成微粒生长模拟过程。初始粒子与凝聚体位置的关系有一种特殊情况,即初始粒子的行走轨迹恰好与凝聚体相切,在本文中对这种情况也按照粘附在一起处理。
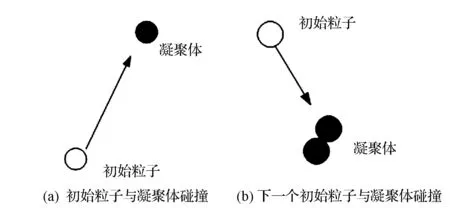
图1 初始粒子与凝聚体碰撞过程
1.2 凝聚体与凝聚体碰撞——枝接过程
图2为凝聚体与凝聚体之间碰撞的枝接过程。当发生枝接碰撞时,每个凝聚体所含碳烟粒子数不再增加,枝接只和两个凝聚体尺寸大小和初始凝聚体的运动轨迹有关。
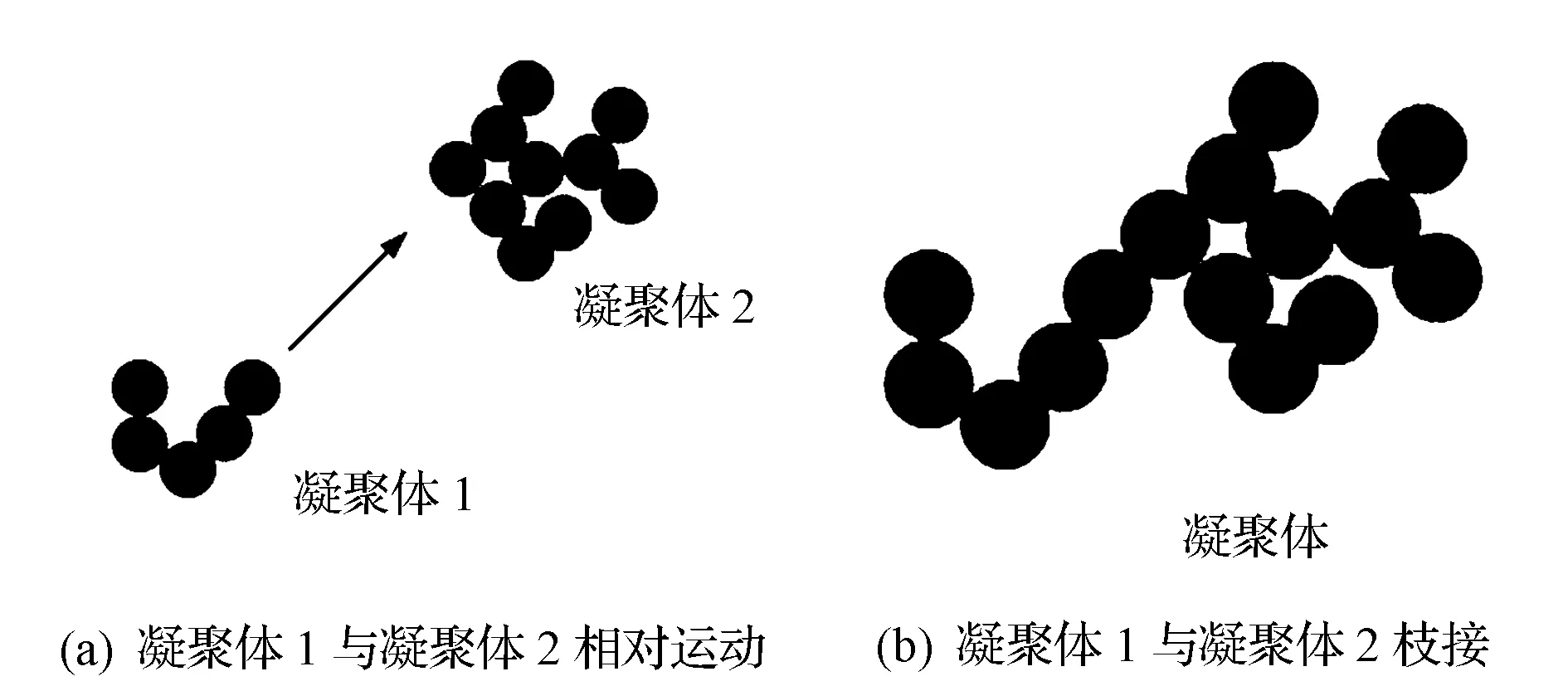
图2 枝接过程
1.3 粒子半径增长量
粒子的表面反应包括粒子的表面生长和表面氧化两个过程。气相组分在粒子表面的生长和沉积使得粒子半径增大,而由OH和O2引起的氧化反应则使粒子半径减小,粒子最终直径的大小是表面生长和氧化过程共同作用的结果。本文中根据粒径增长率和碰撞时间计算出粒子表面生长量。
Knudsen数定义为Kn=2λ/d,λ为系统中粒子平均自由程,d为粒子大小的特征尺度,如粒子的直径。粒子碰撞过程根据Kn数的不同可分为3种模式,分别为
(1)Kn→0:连续介质模式
(2)Kn→:自由分子模式
(3)0.25 连续介质模式下,碰撞频率[10]为 (1) 其中K=2kBT/(3η)式中:kB为玻尔兹曼常数;T为热力学温度;η为气体分子黏度;Ci为连续介质状态的修正系数,Ci=1+1.257Kni;mi为凝聚体i的质量;Cj,mj的含义类似。 自由分子模式下,碰撞频率为 (2) 式中:mc为碳原子质量;ρ为碳烟粒子密度。 介于连续模式与自由分子模式之间的为过渡模式。通常情况下柴油机燃烧压力为6.5MPa,温度为1 500K,对于直径分别为1,2,5和10nm的粒子,Kn数分别为5.2,2.6,1.0和0.5,其值介于0.25和10之间[11],为过渡模式。过渡模式碰撞频率可取自由模式和连续模式碰撞频率的平均值,无量纲化后的表达式[7]为 (3) 其中 第i个和第j个凝聚体发生第n次碰撞所经历的时间为 (4) 式中:N为第n次碰撞时刻的粒子数密度。凝聚经历的总时间为tn+1=tn+Δti,j。 粒子的表面生长反应促进了粒子半径的增加,进而使整个凝聚体半径增加,粒子半径R随时间t的变化率可用粒径增长率来描述,即 dR/dt=Ω (5) 式中:Ω为粒径增长率。黑体字符代表有量纲的变量,下同。将式(5)的各个参量无量纲化处理,令 (6) 式中:R0为出现在模型中第一个粒子的半径;t0为粒子间发生第一次碰撞经历的时间。对式(5)进行变换: (7) 结合式(5)和式(6),式(7)可变为 (8) 结合式(8),R对于t的1阶泰勒展开式为 即R(t+Δt)-R(t)=ΩΔt,或写为 ΔR=ΩΔt (9) ΔR即为每次碰撞事件发生时粒子表面增加的厚度。 由于粒子表面增长,碳烟粒子间存在交叉重叠,在计算凝聚体的体积、表面积和回转半径等参量时,如果只是把每个粒子对应参量值简单相加,则随着碳烟粒子数的增加,计算误差逐渐增大。为了减小这种计算误差,采用蒙特卡洛取样算法[12]。定义碳烟粒子数为n的凝聚体中每个碳烟粒子为B1,B2,…,Bn,随机选择凝聚体内的一个碳烟粒子Bn,并在此粒子内部随机选择一个点pm,建立一个关于pm,Bn的函数f(pm,Bn),m为粒子Bn内随机选择的点的序号,根据粒子数n等信息计算出取样点的数量M。当pm点落入Bn编号为最小的粒子内时,此时f(pm,Bn)=1,当pm点落入Bn编号不是最小的粒子内时,则f(pm,Bn)=0,粒子就不被计数,即 f(pm,Bn)= (10) 凝聚体表面积计算采用类似的算法,不同之处在于所选择的点必须位于粒子表面上。 (11) 则凝聚体回转半径Rg为 (12) 欧氏空间用1,2,3这样的整数表示线、面、空间的维数,却无法表示非规则、自相似的几何图形的维数,比如测定海岸线的长度等。分形维数可以表示分形集的不规则程度,突破了维数为整数的界限,一般为分数。 随着研究的深入,分形理论逐渐应用到物理学、化学、生物学、天文学和经济学等,为许多问题的解决提供了新的思路和方法。分形维数的表示方法有很多,本文中采用的分形维数Df表示为 (13) Df=slope{lnri, lnVri} (14) 本文中应用C++语言编程构建了粒子碰撞凝聚的计算模型。以柴油机工作过程的温度、压力、粒子数密度、C2H2沉积速率、O2和OH的氧化速率等作为初始数据[7],对碳烟粒子碰撞凝聚生长过程进行了数值模拟。 4.1 凝聚碰撞 在环境压力保持不变的情况下,分3种情况对比表面反应对粒子凝聚过程的影响:C1无表面生长和氧化;C2只有表面生长;C3有表面生长和氧化。 图3是在粒子数为400时计算得到的上述3种情况下凝聚体形态图。通过对比可知,对于图3(a),粒子直径始终不发生变化,凝聚体内部粒子大小和外部粒子大小一致;对于图3(b),只存在表面生长,凝聚体内部粒子先于外部粒子粘附在凝聚体上,随着碰撞过程进行,内部粒子在空间环境中存在的时间较长,粒径增长较大,所以粒子交叉重叠现象明显;而外部粒子在空间环境中存在时间较短,所以粒径增加较小,交叉重叠现象较弱。对于图3(c),同时存在表面生长和氧化反应,凝聚体交叉重叠情况相对C2较弱,凝聚体包容半径相对于C2也较小,但由于氧化作用在整个粒子凝聚过程中所占比重较小,与图3(b)相比不是特别明显,这在图4中进一步得到了证实。 图3 3种情况下凝聚体的形态 图4是在粒子数n为750,环境压力为1MPa的情况下凝聚体参量的变化,由于存在随机波动,故进行了50次重复计算,然后对计算结果进行平均处理。通过图4(a)看出,C1与C2和C3情况相比,凝聚体分形维数较小。这是因为,一方面由弹射凝聚模型特点造成凝聚体结构较松散,另一方面粒子间不存在交叉重叠情况;另外C1曲线后期略有上升是因为有少量粒子进入凝聚体内部导致凝聚体变得更加致密。在C2和C3两种情况下,在碰撞初期分形维数变化较大,主要是因为当第一个初始粒子出现在空间成为凝聚体时,分形维数为3。但当少数粒子碰撞粘附在一起后,凝聚体结构较松散,粒子间交叉重叠不明显,分形维数较低。而随着粒子表面生长和氧化反应的继续进行和粒子的不断填充,凝聚体更加致密和接近于团簇状,使分形维数又有较大提高。C3与C2相比,还存在粒子的表面氧化,使粒子的密实程度降低,分形维数也有一定程度降低。图4(b)是凝聚体的最小包容半径随粒子数的变化,可知,最小包容半径初期增加较快,后期增加较慢,主要是初期凝聚体半径相对初始粒子半径比例较小,所以粘附到凝聚体的初始粒子体积对凝聚体体积影响较明显,当凝聚体粒子数较多时,整个凝聚体包容半径达到30以上,而此时初始粒子半径只有1,对凝聚体包容半径影响较小,所以随着粒子继续增加,凝聚体包容半径增长减慢。图4(c)为凝聚体体积随粒子数的变化,对于C1情况,凝聚体体积就是单个粒子体积乘以粒子数,所以图线呈线性增长;而对于C2和C3,凝聚体体积的增大除了粒子增长的因素之外,表面生长的影响也较大,这可以从图4中看出,所以C2和C3曲线与C1曲线的差别较大;而C2和C3曲线之间也有差别,说明表面氧化对凝聚体体积也有影响。由于C2和C3两种情况后期表面反应都大大减弱,粒子半径增大越来越不明显,所以两条曲线后期斜率基本保持不变,且凝聚体体积增长和粒子数近似呈线性关系。 图4 凝聚体参量值在3种情况下的对比 图5 环境压力变化对凝聚过程参量的影响 图6为粒子碰撞过程中有表面生长和氧化,环境压力保持在1MPa,不同温度下粒子的凝聚过程。由图6(a)可见,随着温度增加,粒子碰撞频率减小。由图6(b)可见,由于C2H2沉积速率先增大后减小最后趋于稳定,O2和OH的氧化速率一直减小最后趋于稳定,且表面生长速率大于表面氧化速率,两者共同作用的结果使得粒径增长率先增大后减小,对应图上出现了一个峰值,后期表面生长速率趋于稳定而氧化速率的影响较弱,且后期碰撞粒子直径较小,所以对应粒径增长率缓慢增加。温度升高导致碳烟表面氧化速率比生长速率增加的更快,故粒径增长率减小。图6(c)为凝聚体分形维数随粒子数变化关系,整体变化趋势同图5(c)。由于粒径增长率随温度升高而降低,致使凝聚体致密程度降低,所以分形维数减小。 图6 温度变化对凝聚过程参量的影响 4.2 枝接碰撞 图7是通过枝接形成的凝聚体的形态图,发生枝接凝聚的4个小凝聚体所含粒子数分别为106,119,121和137,总和为483个。图7(a)为无表面生长和氧化过程,图7(b)为伴随有表面生长和氧化过程。可以看出,通过枝接过程形成的凝聚体具有明显的链状结构,同样,表面生长和氧化可以改变凝聚体的致密程度和分形维数等参数,表1给出了凝聚体的相应参数。 图7 两种情况下枝接形成的凝聚体形貌 分类粒子数n分形维数Df包容半径Re回转半径Rg无表面生长和氧化4832.02432.87216.790有表面生长和氧化4832.25066.80327.031 图8为柴油机排放尾气中的碳烟颗粒物形貌照片[13],其中大部分为链状结构,而且较大的链状结构中包含着较小的链状结构,较小的链状结构中还包含有更小的链状结构,呈现分形的自相似性。由图3、图7和图8对比可知,通过枝接过程模拟出的碳烟结构更接近于尾气中真实的链状碳烟形貌并具有分形特征。 图8 真实柴油机排放产生的碳烟形貌 应用弹射凝聚模型和蒙特卡洛方法构建了碳烟颗粒凝聚和表面生长的数学物理模型,并以分形维数描述凝聚体生长过程和形貌特征,根据不同条件进行一系列数值求解,得到以下结论。 (1) 碳烟的表面生长会明显提高凝聚体的分形维数、包容半径和凝聚体体积,并使凝聚体变得更加致密,表面氧化则起相反作用。 (2) 随着环境压力的升高,粒子碰撞频率减小且波动性减弱,导致分形维数增大;随着环境温度的升高,粒子的粒径增长率减小,导致分形维数降低。 (3) 通过与柴油机尾气中真实碳烟照片对比可知,枝接过程模拟出的碳烟结构更接近于尾气中真实的链状碳烟形貌并具有分形特征。 通过上述结论可以看出,利用碳烟颗粒的形貌特征能够获得燃烧环境和燃烧过程的相关信息,如表面反应、压力和温度影响等情况,从而为优化燃烧、降低碳烟提供依据。 [1] FENG T, REITZ R D, FOSTER D E, et al. Nine-step Phenomenological Diesel Soot Model Validated over a Wide Range of Engine Conditions[J]. International Journal of Thermal Sciences, 2009, 48(6):1223-1234. [2] 陈亮, 成晓北, 颜方沁,等. 基于改进的详细碳烟模型的柴油燃烧碳烟颗粒物的生成特性[J].燃烧科学与技术, 2013, 19(3): 234-240. [3] 赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟[M]. 北京: 科学出版社, 2008. [4] PATTERSON R I A, WAGNER W, KRAFT M. Stochastic Weighted Particle Methods for Population Balance Equations[J]. Journal of Computational Physics, 2011, 230(19): 7456-7472. [5] WANG H. Formation of Nascent Soot and Other Condensed-phase Materials in Flames[J]. Proceedings of the Combustion Institute, 2011, 33(1): 41-67. [6] FRENKLACH M, HARRIS S J. Aerosol Dynamics Modeling Using the Method of Moments[J]. Journal of Colloid and Interface Science, 1987, 118(1):252-261. [7] MITCHELL P A. Monte Carlo Simulation of Soot Aggregation with Simultaneous Surface Growth[D]. University of California, Berkeley, 2001. [8] CELNIK M, RAJ A, WEST R, et al.Aromatic Site Description of Soot Particles[J]. Combustion and Flame, 2008,155(1-2):161-180. [9] RAJ A, SANDER M, JANARDHANAN V, et al.A Study on the Coagulation of Polycyclic Aromatic Hydrocarbon Clusters to Determine Their Collision Efficiency[J]. Combustion and Flame, 2010,157(3):523-534. [10] KAZAKOV A, FRENKLACH M. Dynamic Modeling of Soot Particle Coagulation and Aggregation: Implementation with the Method of Moments and Application to High-pressure Laminar Premixed Flames[J]. Combustion and Flame, 1998, 114(3-4): 484-501. [11] 崔心存, 金国栋. 内燃机排放净化[M]. 武汉:华中理工大学出版社,1990. [12] KARP R M, LUBY M, MADRAS N.Monte Carlo Approximation Algorithms for Enumeration Problems[J]. Journal of Algorithms in Cognition, Informatics and Logic, 1989, 10(3):429-448. [13] Van GULIJK C, MARIJNISSEN J C M, MAKKEE M, et al. Measuring Diesel Soot with a Scanning Mobility Particle Sizer and an Electrical Low-pressure Impactor: Performance Assessment with a Model for Fractal-like Agglomerates[J]. Journal of Aerosol Science, 2004, 35(5):633-655. Numerical Simulation of Soot Growth Process Based on Monte Carlo Method Che Wei1,2,3, Wei Mingrui1,2& Li Song1,2 1.HubeiKeyLaboratoryofAdvancedTechnologyforAutomotiveComponents,WuhanUniversityofTechnology,Wuhan430070;2.HubeiCollaborativeInnovationCenterforAutomotiveComponentsTechnology,WuhanUniversityofTechnology,Wuhan430070;3.DepartmentofElectronicsandScienceEngineering,HuanghuaiUniversity,Zhumadian463000 The physical model for the collision between soot particles is established based on ballistic aggregation model, and Monte Carlo method is used to build the mathematical model for soot particle aggregation and surface growth, with numerical simulation conducted. Fractal dimension, enclosing radius and aggregate volume are introduced to describe the fractal growth characteristics of aggregates, and the effects of surface growth process on these parameters are analyzed. The effects of different ambient pressures and temperatures on the collision frequency, the growth rate of particle size, and fractal dimension are compared. Finally through a simulation on coalescence process, the morphological feature of chain-like aggregates is obtained and compared with real soot photos. The results show that the soot structure simulated by coalescence process is closer to real morphology of chain-like soot particles in exhaust gas. soot particles; ballistic aggregation; Monte Carlo method; fractal dimension *国家自然科学基金(51276132)和中央高校基本科研业务费专项资金(2015Ⅲ040)资助。 原稿收到日期为2015年5月14日,修改稿收到日期为2015年8月4日。
2 凝聚体参量的蒙特卡洛算法
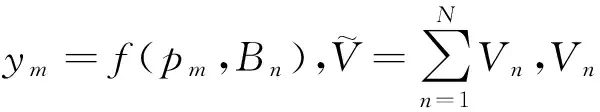

3 分形维数

4 计算结果与分析







5 结论
