混合动力汽车模糊控制策略优化*

李 军，朱亚洲，纪 雷，徐杨蛟

(重庆交通大学机电与汽车工程学院，重庆 400074)

2016002

混合动力汽车模糊控制策略优化*

李 军，朱亚洲，纪 雷，徐杨蛟

(重庆交通大学机电与汽车工程学院，重庆 400074)

本文中基于自适应模糊逻辑算法研究了某款并联混合动力电动汽车的动力传动系统控制策略，以最小化油耗和排放为目标，在Matlab/Simulink平台上建立相应的控制系统模型，并采用遗传算法对模糊控制规则进行离线优化。结果表明，采用遗传算法优化的模糊控制策略具有较好的控制效果，混合动力汽车的燃油经济性和排放得到有效改善。

混合动力汽车；控制策略优化；模糊控制；遗传算法

前言

混合动力汽车能量管理策略一直是汽车领域研究的热点，但目前实现商业化的只有依据工程经验设计的逻辑门限能量管理策略。模糊控制策略具有非线性、鲁棒性和实时性的特点，增加了模糊决策因素，符合人的思维逻辑，应用在混合动力汽车中比较合适[1-2]。控制规则的确定是模糊控制器的关键设计之一，但以往根据专家经验制定的控制规则具有一定的主观性，很难达到全局最优的控制效果。因此，如何对已制定的控制规则进行优化，是混合动力汽车模糊能量管理策略研究的重要方向之一[3]。

遗传算法是根据自然选择和遗传机制构造的搜索算法。该算法能够应用于各类非线性问题的优化，具有全局性、并行性和鲁棒性等优点，比较适合于应用在模糊控制策略的优化中[4-8]。本文中以某传统汽车为原型，进行并联式混合动力汽车动力系统部件选型和参数匹配，并在此基础上研究模糊能量控制系统，然后采用遗传算法对模糊控制规则进行离线优化，最后对优化前后的控制策略进行对比仿真。

1 模糊逻辑控制策略的设计

1.1 并联混合动力汽车主要结构参数

本文中的研究对象为某款混合动力汽车，它具有电机单独驱动、发动机单独驱动、行车充电、混合驱动和再生制动等工作模式。其主要参数如表1所示。

1.2 模糊控制器的设计

为实现对该车能量的优化管理，本文中设计了能量管理系统的模糊控制策略，并采用遗传算法对模糊控制器的控制规则进行多目标离线优化。其模糊控制器的2个输入变量为电池的SOC值和整车需求转矩与当前转速下发动机的最优转矩的差值ΔT，输出变量为系数k。模糊控制器输入、输出变量的模糊子集和隶属度函数采用三角形和梯形相结合的方式。ΔT的5个模糊子集分别为{NB,NS,M,PS,PB}；电池SOC的5个模糊子集分别为{VL,L,N,H,VH}；输出量k的5个模糊子集分别为{VS,S,M,B,VB}。

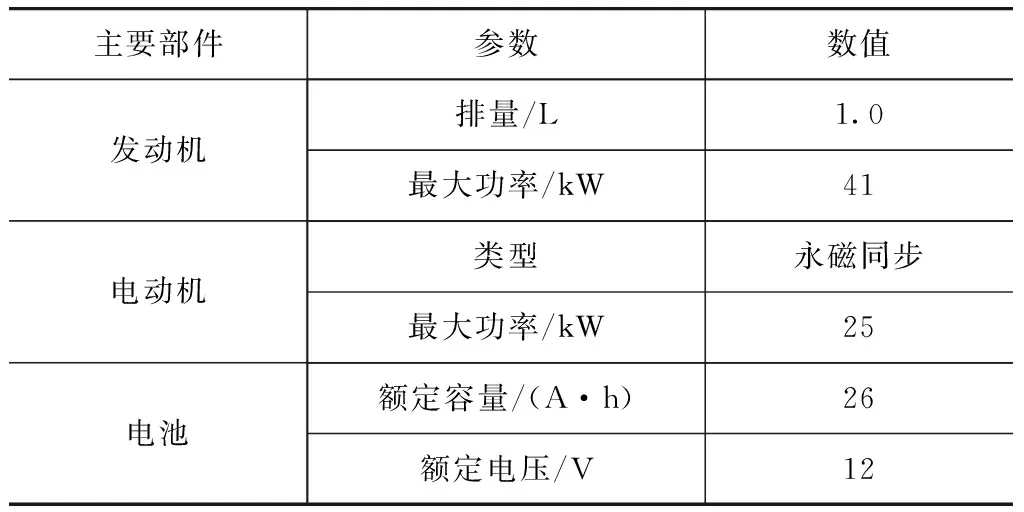
表1 主要部件的仿真参数

在确定各输入、输出变量模糊子集和隶属度函数后，编写出模糊控制规则，见表2。

表2 模糊控制规则表

制定模糊控制规则的主要依据如下：

(1) 当汽车速度低于某一最低速度值时，由电机单独提供驱动转矩；

(2) 当整车需求转矩大于当前转速下发动机输出转矩的最大值时，电机提供补充转矩辅助驱动；

(3) 在给定转速下，当发动机工作于需求转矩且效率较低时，发动机关闭，电机提供需求转矩；

(4) 当电池SOC比较低时，电机利用发动机输出的额外转矩给电池充电；

(5) 当发动机工作在高效区间时，仅由发动机提供转矩。

在模糊推理运算中，与和蕴涵运算采用最小法，或运算采用最大法，结论合成采用累加法，输出解模糊采用面积质心法。

2 遗传算法优化模糊控制器

2.1 用于控制规则优化的遗传算法

对模糊控制器控制规则优化的遗传算法可表示为

GA=(C，J，P0，M，Φ，Γ，Ψ，T)

(1)

式中：C为个体的编码方法；J为个体适应度评价函数；P0为初始种群；M为种群大小；Φ，Γ和Ψ分别为选择算子、交叉算子和变异算子；T为遗传算法的终止条件。遗传算法流程如图1所示。

图1 遗传算法流程

2.2 控制规则编码

遗传算法优化模糊控制规则首先须解决的是规则编码问题。十进制编码染色体长度短，运算速度快、精度高，不产生不可行解，并且对于变异操作的种群稳定性好，因此本文中选择十进制整数编码[9]。

模糊控制器采用双输入单输出模型，每个输入量和输出量都含有5个模糊子集，共有25条控制规则。为保证控制规则的完整性和一致性，只对输出量值编码。采用十进制整数，将输出变量k的变量值{VS,S,M,B,VB}依次编码为1，2，3，4，5，如表2所示的25条控制规则的编码依次为33111，…，55544，由此产生一个有25个染色体组成的个体。

2.3 目标函数

本文中控制策略的优化目标是使油耗和排放量最小化。其目标函数为

(2)

式中：ω1～ω4为优化目标的权重因子；H为油耗值；X为CO排放值；Y为HC排放值；Z为NOx排放值；下标“targ”为它们对应的目标值。

式中的4个目标是相互影响的，单个目标函数达到最优时其他目标函数不一定最优，采用加权法建立目标函数，从而将多目标优化问题转化为单目标优化问题[10]。表3为采用的自定义目标值，其中排放量值参考EURO Ⅴ排放标准。

表3 油耗和排放目标值

2.4 初始种群的产生

初始群体的特性对计算结果和效率有重要影响。标准遗传算法是按预定或随机方法产生一组初始解群体，具有一定盲目性，产生的控制规则个体可能极不合理，影响着进化的进度和精度。借鉴文献[9]中的稳态繁殖思想，将表1中的模糊控制规则作为母体，每位编码按0～0.3的概率为-1,按0.3～0.6的概率为+1,大于0.6的概率不变，产生30个个体，从中选择19个，加上母体共20个，组成初始种群。

2.5 选择、交叉和变异过程

选择算子的作用是从当前代的群体中选择出一些比较优良的个体，并将其复制到下一代群体中。本文中采用比例选择算子，每个个体被选中的概率与其适应度的大小成正比。设群体大小为M，个体i的适应度为Fi，则个体i被选中的概率pis为

(3)

根据整数编码的特点，交叉算法选择均匀交叉，即两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换，形成两个新的个体。均匀交叉的主要过程：①随机产生一个与个体编码串长度相等的屏蔽字W=w1w2…wj…wL，其中wj非0即1，L为个体编码串长度；②当wj为0时，2个子代第j个基因座上基因值保持不变；当wj为1时，2个子代分别继承两父代交叉后的第j个基因座上基因值。

变异操作选择基本位变异，对个体的每一个基因座，以变异率指定其为变异点。对于每个指定的变异点，采用随机进行加1或减1的变异方法，如果该基因值为最小值或最大值则分别只进行加1或减1操作，即

(4)

3 结果分析

为验证优化后控制策略的有效性，基于美国再生能源实验室在Matlab/Simulink软件环境下开发的电动汽车仿真软件ADVISOR2002，建立并联混合动力汽车仿真模型。同时为验证优化控制策略的工况适应性，选择两个典型工况进行仿真分析，即欧洲驾驶循环(NEDC)和美国城市道路循环(UDDS)。

分别运用ADVISOR和Matlab软件进行参数仿真和离线优化。首先以专家经验建立的模糊控制策略对混合动力汽车系统进行仿真，然后采用遗传算法对模糊控制器控制规则进行多目标优化，遗传算法运行参数选择如表4所示。

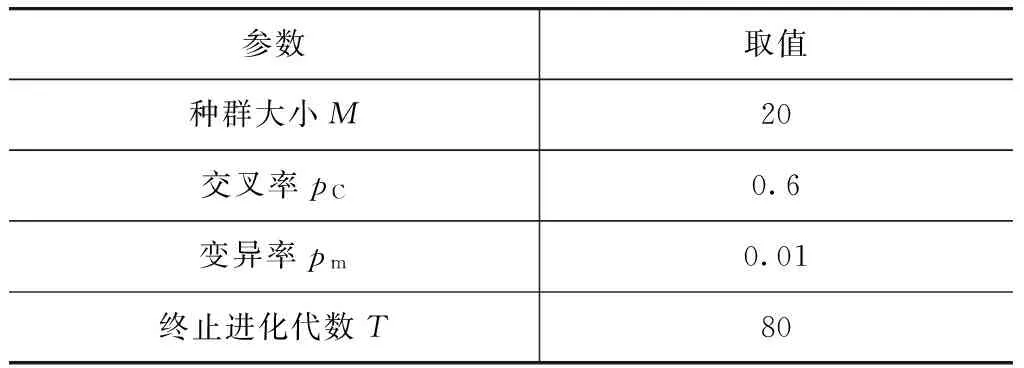
表4 遗传算法运行参数

两种工况下控制策略优化前后仿真结果对比情况如表5和表6所示。由表可见，优化后车辆的百公里油耗和排放量都有所降低，其中NEDC工况下百公里油耗下降了7.01%，排放值分别下降了1.17%(HC)，1.04%(CO)和5.42%(NOx)；UDDS工况下百公里油耗下降了3.0%，排放值分别下降了1.27%(HC)，1.42%(CO)和0.56%(NOx)。

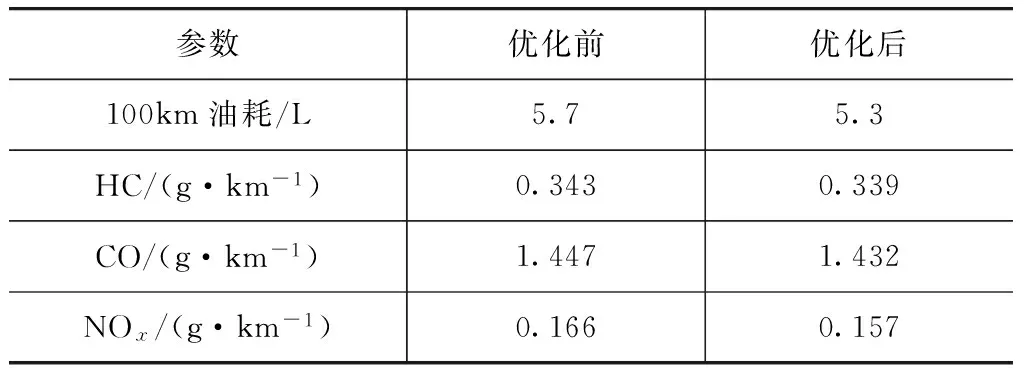
表5 NEDC工况下优化前后仿真结果

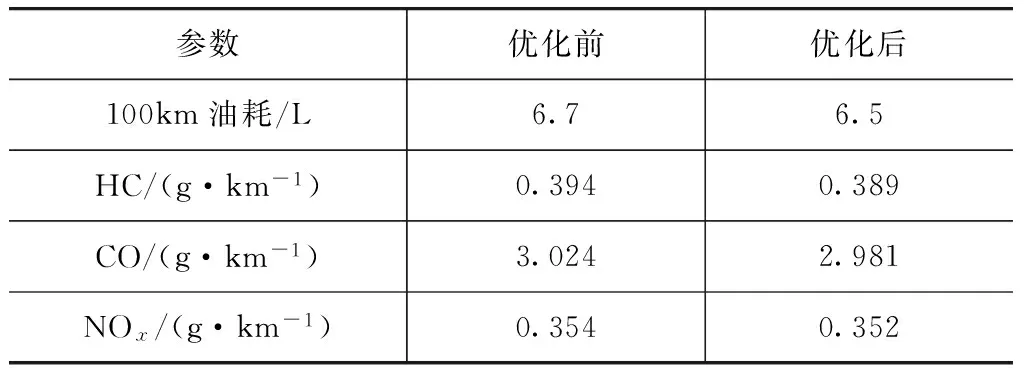
表6 UDDS工况下优化前后仿真结果

图2 NEDC工况下优化前后发动机效率分布

两种工况下优化前后发动机的效率分布分别如图2和图3所示。由图2可见，NEDC工况下优化后的发动机效率在前一段仿真时间有明显提高，这主要是因为这段时间汽车运行工况较复杂，根据经验制定的控制策略无法达到最优控制；由图3可见，UDDS工况下优化后发动机的工作点分布范围相对更加集中，整体效率提高。

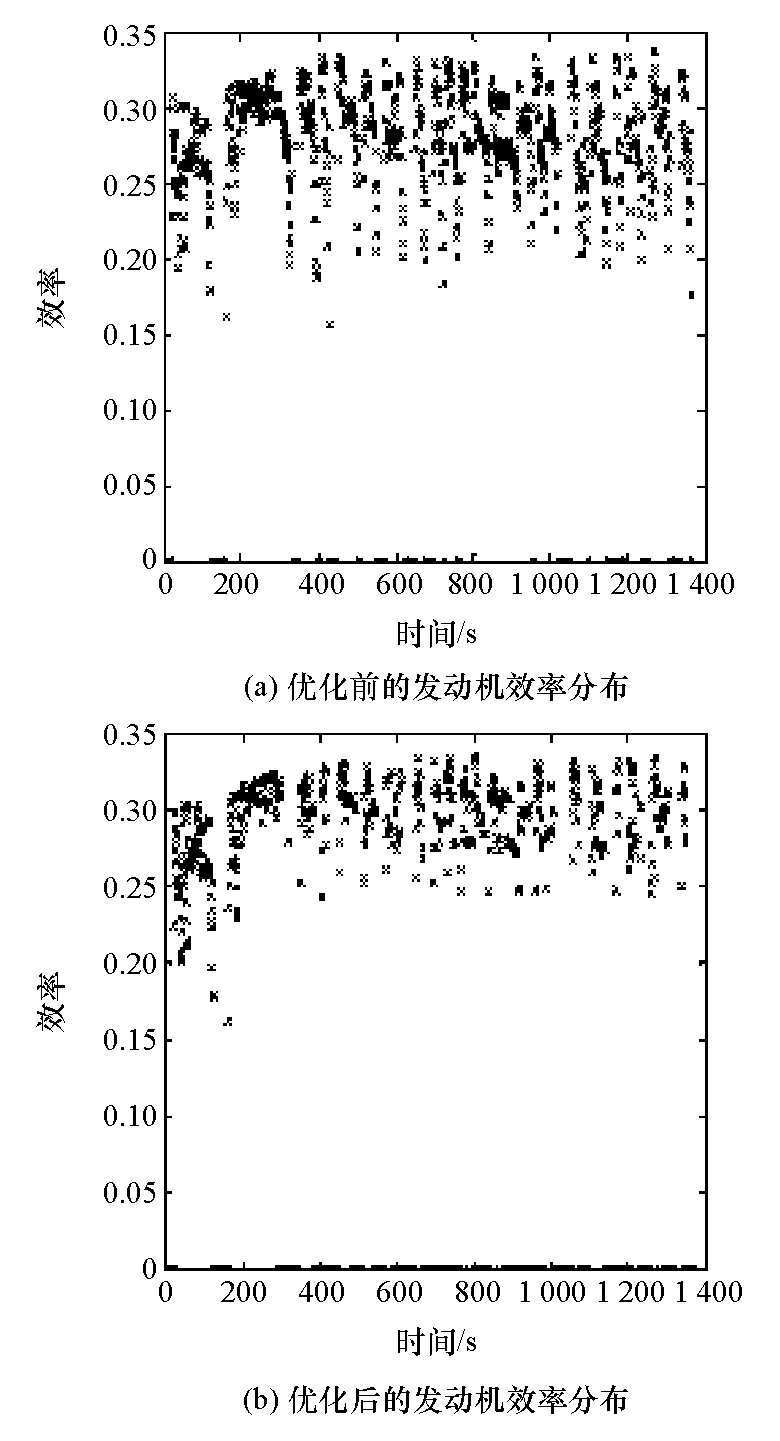
图3 UDDS工况下优化前后发动机效率分布

两种工况下仿真过程中蓄电池SOC变化情况分别如图4和图5所示。优化前后SOC的初始值都为0.7，NEDC工况下优化前后的SOC结束值分别为0.684和0.693，UDDS工况下优化前后的SOC结束值分别为0.712和0.705。不同工况下优化前后SOC变化范围都较小，保证了电池的充放电平衡。

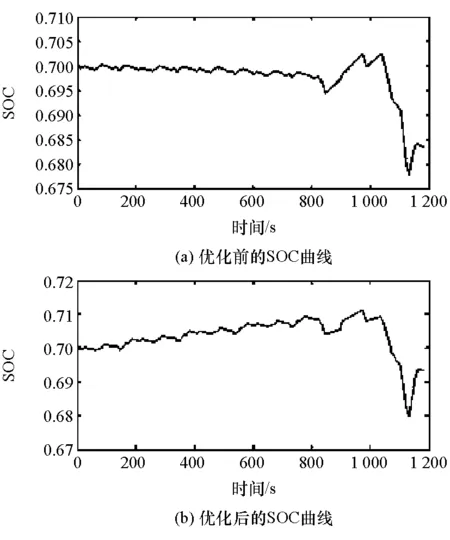
图4 NEDC工况下蓄电池SOC变化曲线

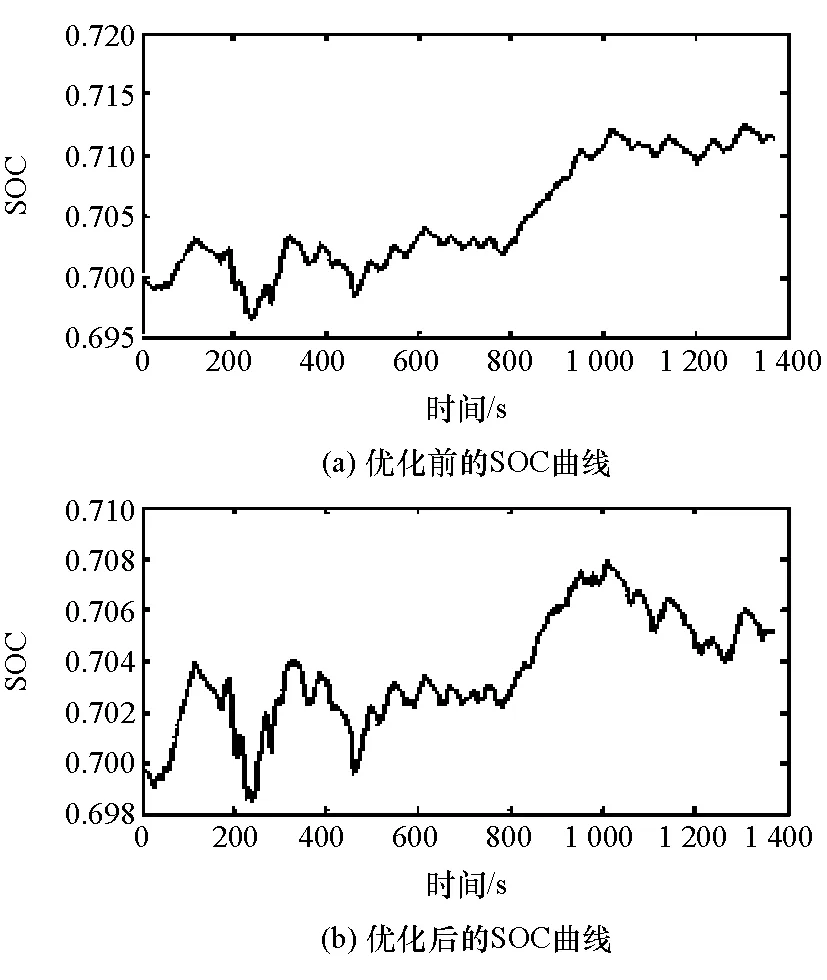
图5 UDDS工况下蓄电池SOC变化曲线

两种工况下遗传算法优化过程目标函数值的变化曲线分别如图6和图7所示。图6中采用遗传算法优化到25代左右时，目标函数变化已经很小，约30代以后目标函数基本不再变化；图7中目标函数在约18代以后就基本不再变化。两种工况下仿真优化后的结果比较合理，已达到全局最优解目标。

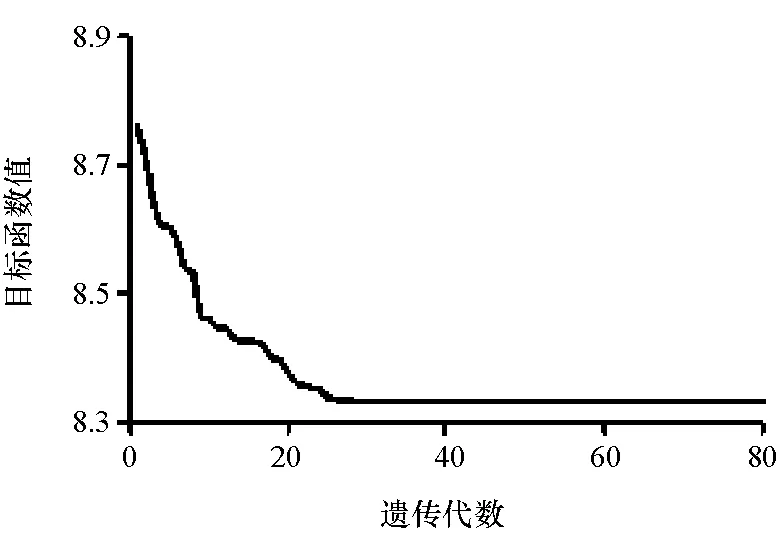
图6 NEDC工况下目标函数收敛曲线

图7 UDDS工况下目标函数收敛曲线

两种工况下采用遗传算法优化后的模糊控制规则分别见表7和表8。其中表7中优化后运行工况更多地集中在发动机高效区间，即M集合内。

表7 NEDC工况仿真优化后的模糊控制规则表

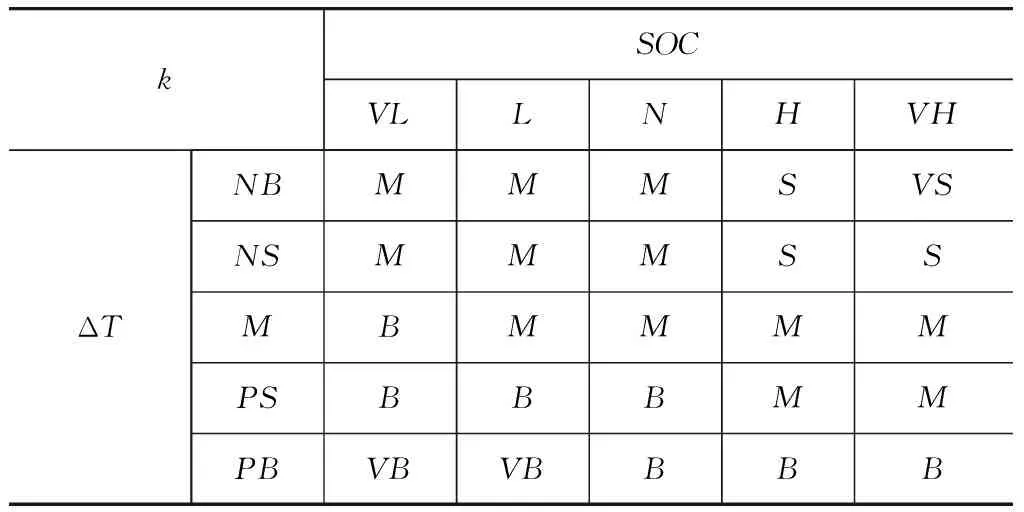
表8 UDDS工况仿真优化后的模糊控制规则表

4 结论

(1) 针对某并联式混合动力汽车，设计了能量管理系统模糊控制策略，并采用十进制遗传算法对模糊控制器的控制规则进行多目标离线优化。

(2) 分别在NEDC工况和UDDS工况下对优化前后的控制策略进行了仿真分析，其中NEDC工况优化后百公里油耗下降了7.01%，UDDS工况下百公里油耗下降了3.0%，两种工况优化后的排放值也都有不同程度的降低。仿真结果表明，针对不同工况下模糊控制策略的优化，遗传算法有较好的适应能力，能够在一定程度上改善并联混合动力汽车的油耗和排放。

[1] LI Chunyan, LIU Guoping. Optimal Fuzzy Power Control and Management of Fuel Cell/battery Hybrid Vehicles[J]. Journal of Power Sources,2009,192(2):525-533.

[2] 吴晓刚,王旭东,毛亮.ISG型混合动力汽车能量管理模糊控制的研究[J].汽车工程,2011,33(7):558-562.

[3] 朱元,田光宇,等.混合动力汽车能量管理策略的四步骤设计方法[J].机械工程学报,2004,40(8):127-133.

[4] PALADINI Vanessa, DONATEO Teresa, dE RISI Arturo, et al. Super-capacitors Fuel-cell Hybrid Electric Vehicle Optimization and Control Strategy Development[J]. Energy Conversion and Management,2007,48(11):3001-3008.

[5] AMIRI Meisam, ESFAHANIAN Mohsen, HAIRI-YAZDI Mohammad Reza, et al. Minimization of Power Losses in Hybrid Electric Vehicles in View of the Prolonging of Battery Life[J]. Journal of Power Sources,2009,190(2):372-379.

[6] POURSAMAD Amir, MONTAZERI Morteza. Design of Genetic-fuzzy Control Strategy for Parallel Hybrid Electric Vehicles[J]. Control Engineering Practice,2008,16(7):861-873.

[7] 张昕,宋建峰,等.基于多目标遗传算法的混合动力电动汽车控制策略优化[J].机械工程学报,2009,45(2):36-40.

[8] 杨世春,朱传高,等.并联式混合动力汽车遗传模糊控制策略的研究[J].汽车工程,2011,33(2):106-111.

[9] 邵克勇,张鸿雁,李飞,等.一种基于GA的模糊控制规则优化新方法[J].化工自动化及仪表,2011,38(3):261-264.

[10] 浦金欢,殷承良,张建武.遗传算法在混合动力汽车控制策略优化中的应用[J].中国机械工程,2005,16(7):648-651.

[11] 乔孟丽,张景元,温莹莹.一种基于遗传算法的模糊控制规则的优化方法[J].计算机测量与控制,2006,14(10):1349-1351.

Optimization of Fuzzy Control Strategy for Hybrid Electric Vehicle

Li Jun, Zhu Yazhou, Ji Lei & Xu Yangjiao

SchoolofMechatronics&AutomotiveEngineering,ChongqingJiaotongUniversity,Chongqing400074

Based on adaptive fuzzy logic algorithm, the control strategy for the power transmission system of a parallel hybrid electric vehicle (PHEV) is studied. A corresponding control system model is built and an off-line optimization on fuzzy control rule is conducted by using genetic algorithm, with minimizing fuel consumption and emissions as objective. The results show that the fuzzy control strategy optimized with genetic algorithm has better control effects, with the fuel consumption and emission of the PHEV effectively improved.

HEV; control strategy optimization; fuzzy control; genetic algorithm

*国家自然科学基金(51305472)和重庆市自然科学基金重点项目(CSTC2013yykfB0184)资助。

原稿收到日期为2014年7月10日，修改稿收到日期为2014年8月27日。