基于三维激光雷达的智能车辆目标参数辨识*

王 肖，李克强，王建强，徐友春

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084; 2.军事交通学院军用车辆系，天津 300161)

2016179

基于三维激光雷达的智能车辆目标参数辨识*

王 肖1,2，李克强1，王建强1，徐友春2

(1.清华大学，汽车安全与节能国家重点实验室，北京 100084; 2.军事交通学院军用车辆系，天津 300161)

智能车周围车辆目标参数(位姿、运动速度和几何形状)对智能车路径规划和决策算法而言至关重要。选取三维激光雷达作为传感器，对车辆目标位置、航向角、速度和几何形状进行计算和滤波。针对车辆目标点云受观测点位置和自遮挡等因素的影响，提出一种动态参考点模型用于计算目标速度；对于目标航向角，采用先点云分块聚类后主成分拟合的思路来提高航向角精度；提出一种基于几何形状变化速率的滤波算法来解决几何形状不易测量和复杂多变等问题。分别就车辆目标速度、航向角和几何形状进行实验分析，结果证明基于本文方法的参数计算结果能获得较高精度，满足智能车环境感知要求。

智能车辆；三维激光雷达；参数辨识；动态参考点；几何形状变化速率

前言

三维激光雷达能捕获目标物基本形状特征和丰富局部细节，且具有可靠性和测量精度高等优点，被广泛应用在智能车辆环境感知中。作为感知的重要内容，车辆目标的位姿、运动速度和几何形状是智能车辆路径规划和决策算法的基础。由于三维激光雷达固有特性，目标点云分布受到观测点位置和自遮挡等因素的影响，使参数难以精确计算。

国内外学者对车辆目标参数计算做了许多研究。文献[1]中综合利用盒子模型和点模型对动态障碍目标进行形状及运动学属性描述，其中盒子模型主要用于车辆目标，其参数包括目标位置、行驶方向和速度等，而点模型用于描述行人等非车辆目标。文献[2]中建立了描述车辆目标长、宽和中心点位置的几何模型，考虑到观测位置改变对目标点云带来的影响，提出一种中心点更新算法来进行校正。文献[3]在以上基础上建立了包含目标中心点位置、形状、行驶方向和速度的盒子模型，同样采用中心点更新算法来弥补观测位置变化和遮挡可能带来的影响。

以上研究主要集中于目标中心位置计算上，而未涉及目标姿态的计算。文献[4]在栅格单元和连通区域标记基础上，提出一种二维包围体(Bounding-box)来容纳所有各个连通区内栅格单元，而后采用主成分分析计算包围体内点云的特性向量，选用对应特征值较大的特征向量方向作为包围体的行驶方向。文献[5]在此基础上，改进采用定向包围体来对目标进行描述。首先采用统计分析方法去除异值点云，而后找出剩余点云主要成分分布方向。考虑目标自遮挡特性，主成分分析算法往往不能获得目标真实运动方向，因此采用随机抽样一致性算法来拟合点云分布的直线模型。该方法关键步骤在于如何去除异值点云，但文中没有给出具体步骤。

车辆目标速度是目标跟踪研究的重要内容。跟踪算法主要研究点为运动模型、数据关联和滤波算法。常速度模型是最简单、应用最广泛的运动模型[2-3,6]，其线性特性使之可直接应用卡尔曼滤波器进行数据预测和更新[3]。而粒子滤波由于其适用于非线性运动模型非单高斯状态假设中，也得到一定应用[2,6]。数据关联算法主要包括最近邻(NN)[7]、全局最近邻(GNN)[8]、联合概率数据关联(JPDA)[9]和多假设跟踪算法(MHT)[10]等，其中最近邻算法由于其简单高效，适合于应用在目标稀疏场景中，而联合概率数据关联和多假设跟踪算法虽能提高复杂场景下关联准确率，但其效率和资源耗费等问题突出。

以上研究结果表明：(1)车辆目标位置通常利用包围体中心点来表示，但由于观测点位置和自遮挡因素影响，使中心点位置难以精确计算，这导致后续目标速度计算误差较大；(2)车辆目标航向角研究较少，由于点云分布的复杂性，常规拟合方法效果较差；(3)车辆几何形状通常采用固定的先验参数。

针对以上问题，本文中提出一种动态参考点模型来计算目标速度，相对于中心点，该模型参考点具有可直接观测、动态切换等优点；在目标航向角计算中，采用分块聚类、主成分拟合的方法来提高参数精度；提出一种几何形状变化速率方法，并结合卡尔曼滤波器来估计车辆实时几何参数。最后基于最近邻关联算法和在线卡尔曼滤波器对目标参数进行跟踪优化。通过速度、航向角和几何形状3组实验对以上方法进行验证和分析。

1 参数表示

车辆目标采用矩形定向包围体(oriented bounding box, OBB)表示，如图1所示。在雷达坐标系Oxy下，t时刻目标参数可表示为Bt=(Xt,vt,Gt)，其中Xt=(xrt,yrt,φt)为位姿模型，xrt,yrt表示目标参考点坐标，航向角φt为行驶方向同x轴夹角；vt=(vxt,vyt)表示目标沿两个坐标轴行驶速度；Gt=(lt,wt,xct,yct)为目标几何形状模型，其中lt和wt为t时刻测量的包围体长和宽，xct和yct为包围体中心点坐标。

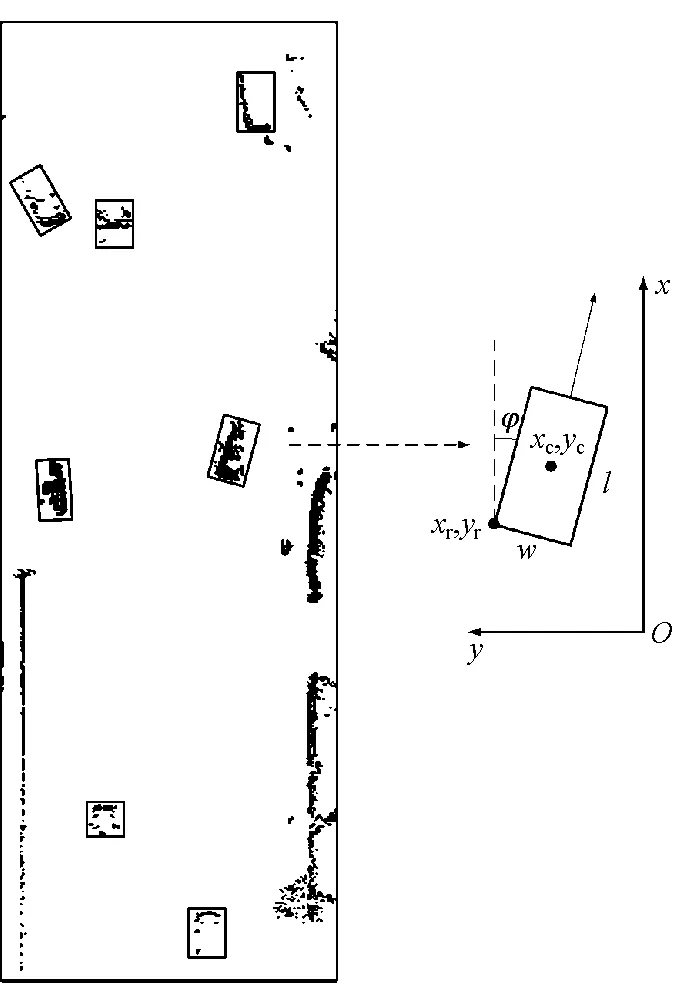
图1 定向包围体参数示意图

2 参数计算

2.1 位姿计算

已知t时刻目标位姿表示为Xt=(xrt,yrt,φt)，其中参考点xrt,yrt用于计算目标速度。通常参考点选取包围体中心，但由于受观测点位置和遮挡等因素影响，中心点坐标往往无法精确计算，这使后续以中心点位置差分方法计算出的目标速度严重失真。为此提出一种不受观测位置和目标自遮挡影响的动态参考点模型。

目标航向角φt同样受观测位置和自遮挡的影响，为此提出一种先分块聚类、后主成分拟合的方法来提高航向角精度。

2.1.1 动态参考点模型

点云分布特性导致难以使用包围体中心作为参考点，但无论目标处于什么位置，总可以找到一个可直接观测的包围体角点并将此作为参考点(暂不考虑目标间相互遮挡的影响)，同时随着位置的改变该参考点可以动态更新，这便是动态参考点模型的基本原理[11]。

参考点选择和更新的基本思想见图2。将雷达坐标系识别区域分为A1,A12,A2,A23,A3,A34,A4和A148个矩形子区域。可知在Ai=1,2,3,4区域包围体由于自遮挡导致部分尾部和侧部数据丢失，称此区域为自遮挡区。而在区域A12和A34则能够获取较准确的车辆长度参数，区域A14和A23则能够获取较准确宽度参数，称此区域为半自遮挡区。动态参考点选择遵循以下准则。

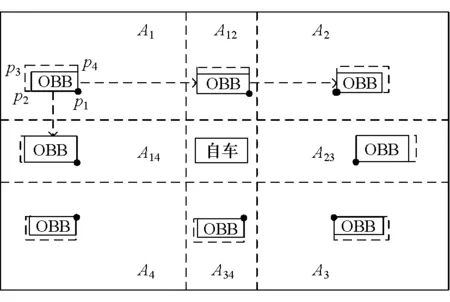
图2 动态参考点选择示意图

(1) 初始化动态参考点 当t时刻目标车辆位于Ai=1,2,3,4区时，选择定向包围体与自车最近邻角点作为参考点(xrt,yrt)，如图中位于A1区中的角点p1。

(2) 参考点保持 当定向包围体当前时刻仍处于自遮挡区时，则参考点(xrt,yrt)仍为上一时刻包围体角点；当包围体上一时刻和当前时刻皆位于自遮挡区时，则参考点(xrt,yrt)仍为上一时刻包围体角点，如图中A1～A12参考点保持不变。

(3) 参考点切换 当包围体进入新的自遮挡区时，则更新动态参考点。例如当包围体从A12至A2时，参考点从p1更换为p2，同理当从A14至A4时，参考点从p1更换为p4。

2.1.2 基于分块聚类、主成分拟合的航向角计算

在复杂行驶环境中，目标经常出现切入、转向等行为，这要求智能车必须能够快速、准确地识别其行驶航向角。

目标航向角计算有两种思路：一是利用参考点变化方向来计算；二是根据点云分布特征来分析。第一种方法缺点是无法分析静态和低速目标，且难以适用于车辆转向场景中。

本研究采用第二种方法进行研究，其主要思路是转化为二维平面上点云主成分方向直线拟合问题。采用随机抽样一致性算法[5]来拟合点云的直线模型，但该方法受点云分布影响较大。考虑到车辆点云平面形状主要呈“L”和“I”型，如图3所示，如果能够将表征航向角的主要部分提取出来作为感兴趣区域(ROI)，并基于该区域进行拟合，这无疑比利用整体点云拟合精度更高。

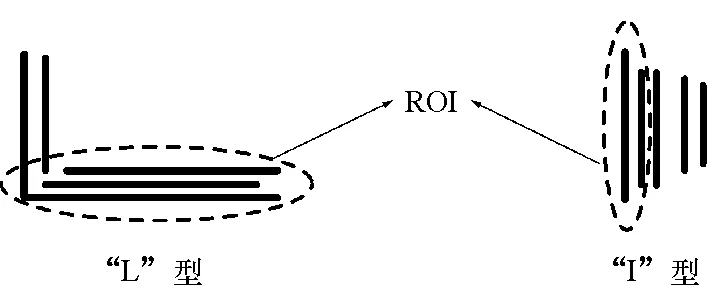
图3 “L”和“I”型点云感兴趣区域

基于此思想提出先利用混合高斯(GMM)算法将点云分成两部分并从中选取感兴趣区域，而后采用随机抽样一致性(RANSAC)算法对感兴趣区域点云进行拟合，最后再计算航向角。图4为计算过程示意图。具体算法如表1所示。

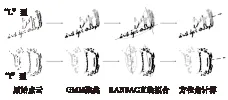
图4 “L”和“I”型点云航向角计算过程

在点云类型计算中(CalculateType函数)，考虑到点云分布主要受目标位姿影响，则可用如下概率来描述：

p(Mt|Xt)=p(Mt|xrt,yrt,φt)

(1)

式中：Mt为目标分布类型(“L”或“I”)；Xt为t时刻目标位姿。基于目标位置与航向角独立性假设，可得

表1 基于GMM和RANSAC

p(Mt|Xt)=p(Mt|xrt,yrt)p(Mt|φt)

(2)

由于此时刻目标方位φt未知，因此采用点云分布方差之比τt来近似替代，视点云为二维高斯分布，则有

(3)

式中σmax和σmin分别为最大和最小正态方差。则可得

p(Mt|Xt)=p(Mt|xrt,yrt)p(Mt|τt)

(4)

对于p(Mt|xrt,yrt)，由于难以用概率密度函数来精确表示，因此采用如下离散经验值：

式中：R1为图2中的并集A14∪A23；R2为剩余区域。

对于p(M|τt)同样采用如下经验值：

最终计算两种目标类型的概率：

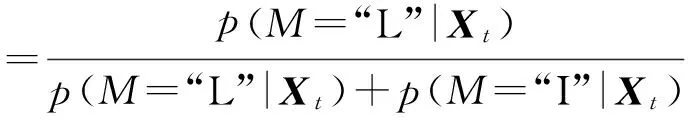
(5)

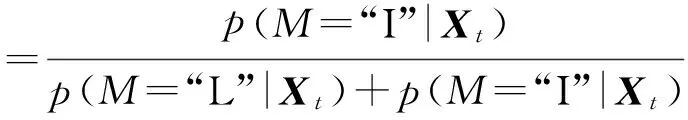
(6)

如果p(M=“L”)>p(M=“I”)则选择“L”模型，反之选择“I”模型。

在第二步聚类算法中，首先采用Kmeans算法进行初始聚类，而后利用GMM算法提升聚类精度。在第三步中则采用RANSAC算法对聚类出的两部分进行直线拟合。最终结合点云类型在拟合直线基础上计算出目标航向角：如对于“L”模型点云，则直接选择较扁平部分(可以两部分高斯模型的方差比作为选择依据)的拟合直线作为航向角方向；对于“I”模型，可选择近邻部分拟合直线的正交直线作为航向角方向。

2.2 速度计算

目标速度可直接利用前后时刻的参考点位置进行差分：

vxt=(xrt-xrt-1+δ(t-tc)(±l))/T

(7)

vyt=(yrt-yrt-1+δ(t-tc)(±w))/T

(8)

式中T为时刻间隔。为防止参考点切换造成速度突变，设置单位冲击函数项δ(t-tc)，其中tc为参考点更换时刻。

2.3 几何形状参数

车辆几何形状参数难以用精确的模型进行描述，需要依靠滤波算法进行优化，在3.3节将对几何参数滤波进行研究，本节首先引入几何形状变化速率的概念。

几何形状变化速率表示单位时间内几何参数的变化程度，如图5所示。假定车辆真实几何尺寸由t-1时刻的实线和虚线两部分组成，受观测位置影响，在t-1时刻观测长宽分别为lt-1和wt-1，t时刻观测长宽分别为lt和wt，则车辆长、宽变化速率分别为

vl=(lt-lt-1)/T

(9)

vw=(wt-wt-1)/T

(10)

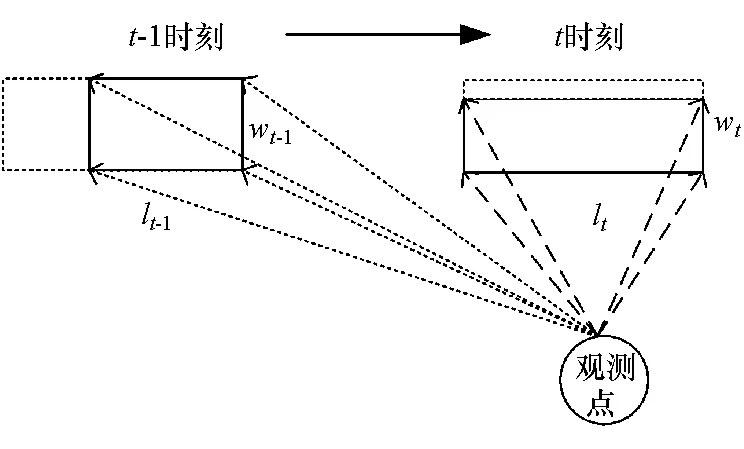
图5 几何形状变化速率示意图

3 参数滤波

3.1 数据关联

数据关联是将当前时刻某一观测目标同上一时刻建立的目标航迹集合中相似度最大的目标进行匹配的过程，通常采用目标位置作为相似度判断准则。本研究采用简单、高效的最近邻方法作为实现算法。

最近邻方法的基本思想是将与被跟踪目标预测位置最近的有效回波作为候选回波：

(11)

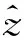
目标下一时刻位置需要利用运动模型进行预测，这将在下节进行研究。

3.2 目标姿态与速度滤波

车辆运动模型包括常速度、常加速度和协调式转向模型等。为简化计算，本研究将车辆运动视为质点平移，不考虑转向运动的影响，采用常速度模型作为基本研究模型，则有

(12)

对于目标方位角，采用常横摆角速度模型，则有

(13)

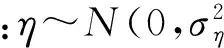
在线滤波基本步骤为：(1)状态预测，基于上一时刻的观测和式(12)，对当前时刻目标位置进行预估，可通过调节噪声方差来改变预估值；(2)目标前后帧关联，基于最近邻关联方法，查找同目标预估位置最近的当前观测，可通过设置适当的关联门限来提高效率和关联准确率；(3)状态更新，通过调节增益值来获取最优滤波结果。

3.3 目标几何形状参数的滤波

基于2.3节提出的几何形状变化速率模型，可建立状态方程：

(14)

同样可利用线性卡尔曼滤波器对各参数进行滤波。需要注意的是，vl和vw大于0说明目标观测长宽递增变化，这意味着观测值越来越接近真实值；而vl和vw小于0则意味着由于自遮挡影响而导致失真。因此目标几何形状的卡尔曼滤波适用于几何形状变化速率大于0的情况下，当变化速率小于0时，应采取形状参数的保优操作以确保逼近真实值，如图6所示。

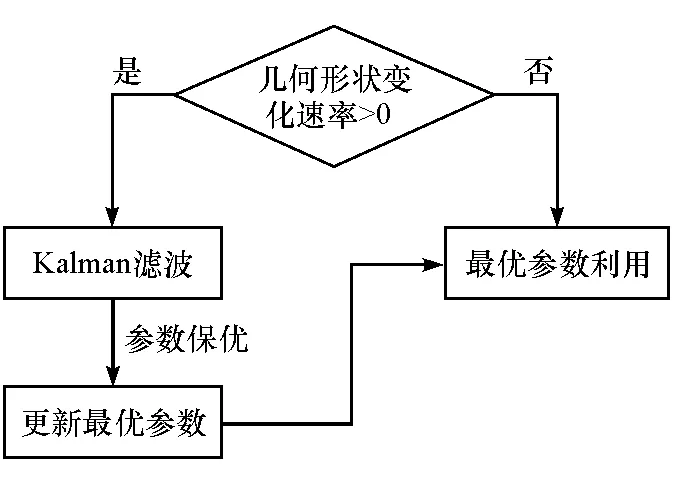
图6 几何参数滤波逻辑

4 实验分析

图7为实验平台，其中传感器包括1台Velodyne HDL-64E三维激光雷达、4个外置和1个内置相机。相机用于记录车外和驾驶员图像，雷达用于采集环境数据，其基本参数为：水平视场360°，垂直视场26.8°，角度分辨率0.09°，测量距离约120m。

图7 实验平台

实验主要通过目标的速度、航向角和几何形状计算来验证本文所提方法，其中涉及的算法参数和预设值如表2所示。

4.1 速度实验分析

由于对未知速度的车辆进行分析无法得到定量的实验结果，因此本实验设置包含定速运动目标和静止目标两组实验场景，如表3所示。

图8为场景1实验结果。图中上方为目标车辆 分别位于智能车左后侧、左侧和左前侧的相机和雷达图，雷达图中心实心矩形表示智能车；图中下方为实验曲线。由图可见，车辆目标估计速度总体平稳，数值在67～74km/h范围内浮动，误差控制在7%以内。值得注意的是，当目标从左后侧行驶至左前侧时，参考点发生了改变，但如图中虚线椭圆中标注，目标速度仍非常平稳，未发生大的突变。

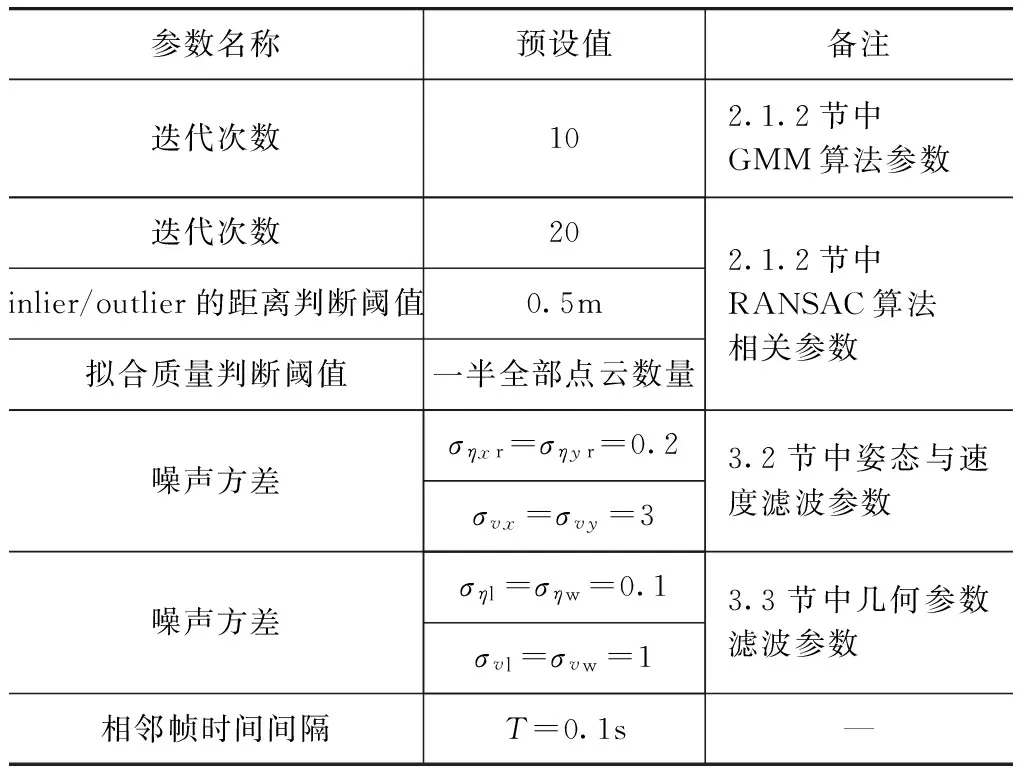
表2 算法参数和预设值

表3 速度实验场景设置

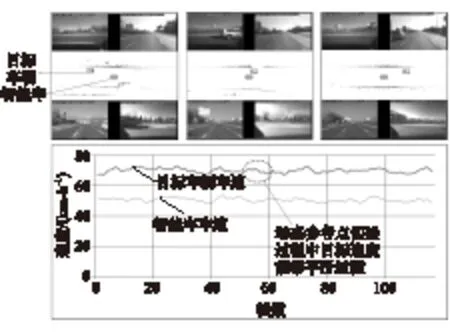
图8 场景1实验结果

图9为场景2实验结果。由图可见：车辆目标估计速度总体平稳，数值在-2～3km/h范围内浮动，基本可认为车辆处在静止状态；同时由虚线椭圆标注处可知，在参考点切换时刻车辆速度估计仍能够保持平稳。

图9 场景2实验结果

由以上两组实验可知，结合动态参考点模型和滤波算法的速度估计在准确度和平稳性方面均能取得较满意效果，能够较好地反映目标真实运动速度；另外参考点切换时刻速度没有跳变现象，这说明式(7)和式(8)中冲击函数项起到关键作用。

4.2 航向角分析

航向角实验场景设置见表4。

表4 航向角实验场景

图10 目标车辆换道切入场景航向角实验结果

图10为实验结果。由图可见：在目标车辆切入过程中，航向角绝对值从0开始逐渐增大(实验中右转航向角为负，左转为正)；当目标逐渐进入智能车所在车道时，航向角开始变小；当目标车辆完全进入目标车道并直行时，其航向角又回归为0，整个过程的航向角变化同实际情况基本相符。在目标处于切入的各个阶段中，其点云形状虽然发生较大变化，但基于本研究提出的分块聚类、主成分拟合的方法依然能够得出较理想的结果。同时整个切入过程的航向角比较平滑，证明滤波算法能够有效地去除识别噪声干扰。

4.3 几何形状分析

几何形状实验场景采用表3中1号场景，即目标车辆从智能车左后侧逐渐行驶至左前侧。

图11为实验结果曲线。由图可见：当目标处于侧后方时，由于受自遮挡影响，其长宽尚不能反映目标真实情况，随着目标逐渐靠近智能车，遮挡影响变小，其长宽也逐渐增加；当到达第25帧左右，宽度值基本达到最理性观测值，到达50帧左右，长度也达到最理想观测值；当车辆继续向前时，由于自遮挡现象再次出现，长宽观测值将变小，但由于算法的保优机制，避免了车辆形状由大变小的逻辑错误，长宽值将保持不变。值得注意的是，车辆宽度开始保持不变点(25帧)早于长度保持不变点(50帧)出现，这是由于当目标位于自遮挡区(图2中A1区)时便能够获取较精确的宽度，而继续前进至半遮挡区(图2中A12区)才能获取较精确的长度，这也从另一方面验证了计算结果的合理性。

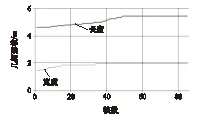
图11 目标车辆换道切入的几何形状实验结果

5 结论

本文中主要对基于三维激光雷达的车辆目标参数进行研究。在参数计算中，提出动态参考点模型来计算目标速度，以消除中心参考点方法受点云分布复杂性影响；对于目标航向角，提出一种先分块聚类，后主成分拟合的方法来提高精度；采用线性卡尔曼滤波器对目标位置、速度和航向角进行优化。针 对目标几何形状难以精确计算的问题，提出几何形状变化速率模型并应用至滤波中。分别就车辆目标速度、航向角和几何形状进行实验分析，结果表明：运动目标速度估计误差控制在7%范围内，静态目标速度估计接近于0；目标换道切入整个过程的航向角变化同实际情况基本相符，同时整个过程的航向角比较平滑；目标几何形状参数能够逐步逼近于真实值，保优机制能够保证获得稳定形状参数。

本研究尚未考虑目标间相互遮挡场景，此时目标点云分布将更加复杂，从而导致参考角点将难以获取，几何形状变化无规律等问题。下一步将重点对此问题进行研究、完善。

[1] FERGUSON D, DARMS M, URMSON C, et al. Detection, prediction, and avoidance of dynamic obstacles in urban environments[C]. Intelligent Vehicles Symposium,2008 IEEE. IEEE,2008:1149-1154.

[2] PETROVSKAYA A, THRUN S. Model based vehicle detection and tracking for autonomous urban driving[J]. Autonomous Robots,2009,26(2-3):123-139.

[3] 杨飞,朱株,龚小谨,等.基于三维激光雷达的动态障碍实时检测与跟踪[J].浙江大学学报(工学版),2012,46(9).

[4] HIMMELSBACH M. LIDAR-based 3D object perception[C]. Proceedings of 1st International Workshop on Cognition for Technical Systems,2008: Munich.

[5] HIMMELSBACH M, WUENSCHE H. Tracking and classification of arbitrary objects with bottom-up/top-down detection[C]. Intelligent Vehicles Symposium (IV),2012 IEEE.

[6] 谌彤童.三维激光雷达在自主车环境感知中的应用研究[D].长沙:国防科技大学,2011.

[7] LI X R, BAR-SHALOM Y. Tracking in clutter with nearest neighbor filters: analysis and performance[J]. Aerospace and Electronic Systems, IEEE Transactions on,1996,32(3):995-1010.

[8] BLACKRNAN S, HOUSE A. Design and analysis of modern tracking systems[M]. Boston, MA: Artech House,1999.

[9] BAR-SHALOM Y, DAUM F, et al. The probabilistic data association filter[J]. Control Systems, IEEE,2009,29(6):82-100.

[10] BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J]. Aerospace and Electronic Systems Magazine, IEEE,2004,19(1):5-18.

[11] 王肖,王建强,李克强,等.智能车辆3-D点云快速分割方法[J].清华大学学报(自然科学版),2014,54(11).

Parameter Identification of Intelligent Vehicle Target Based on 3D Laser Radar

Wang Xiao1,2, Li Keqiang1, Wang Jianqiang1& Xu Youchun2

1.TsinghuaUniversity,StateKeyLaboratoryofAutomotiveSafetyandEnergy,Beijing100084;2.AutomobileEngineeringDepartment，MilitaryTransportationUniversity,Tianjin300161

The parameters of vehicle targets surrounding intelligent vehicle, including the position and pose, movement velocity and geometric shape are important for the path planning and decision making algorithms of intelligent vehicle. With 3D laser radar chosen as sensor, the position, azimuth angle, velocity and geometric shape of vehicle targets are calculated and filtered. In view of that the point cloud of vehicle targets is affected by the position of observation point and self-occlusion, a dynamic reference point model is proposed for calculating target velocity. A scheme of block clustering first then principal component fitting is adopted for increasing the accuracy of azimuth angle, and a filtering algorithm based on the changing rate of geometric shape is proposed to tackle the problem that geometric shape is complex, changeable and difficult to measure. Finally experimental analyse are conducted on the speed, azimuth angle and geometric shape of vehicle targets repsectively with a result verifying that with the parameters calculated by the method proposed, the higher accuracy can be achieved and the requirements of environmental perception for intelligent vehicle can be met.

intelligent vehicle; 3D laser radar; parameter identification; dynamic reference point; changing rate of geometric shape

*国家自然科学基金(51175290)资助。

原稿收到日期为2015年7月20日，修改稿收到日期为2015年8月28日。