一种电力通信网最大不相交双路由配置方法

何玉钧，陈 冉，张文正，刘 毅，周生平



一种电力通信网最大不相交双路由配置方法

何玉钧，陈 冉，张文正，刘 毅，周生平

(华北电力大学电子与通信工程系，河北 保定 071000)

针对现有电力通信网路由算法不能为业务分配双路由的问题，提出一种最可靠环路策略下的最大不相交双路由算法(the maximally disjoint routing algorithm under the most reliable loop strategy, MRMLS)。研究了公共通信网中三种类型的双路由算法，考虑了双路由算法可能面临的网络结构，阐述了采用最大不相交双路由算法的必要性。分析了最大不相交双路由的可靠性，并采用最可靠环路策略完成最大不相交双路由的分配工作。改进了原有最大不相交双路由算法，使所提算法充分考虑节点与链路的可靠性。仿真实验将MRMLS与其他两种方法进行对比，验证了MRMLS的可行性与有效性。

电力通信网；双路由；最大不相交；可靠性；最可靠环路

0 引言

电力通信网是服务于电力系统的通信专网，它的通信业务具有高级别的可靠性需求[1]。为保障业务安全可靠地运行，电力通信网中部分业务需要配置主备用双路由，例如：线路继电保护业务、安全稳定控制等业务具有高级别的安全等级，通常需要配置双路由[2]。双路由的配置可以极大地提高业务的可靠性，当主用路由出现故障时，可迅速将业务切换到备用路由，提高业务应对突发事件的能力，保障通信业务安全可靠地运行[3]。目前电力通信网的路由算法主要关注单路由分配问题，相关研究主要采用改进的Dijkstra算法[2]、Floyd算法[4]、K- shortest paths算法[5]、遗传算法[6-7]与粒子群算法[8-9]等方法完成路由分配工作。但单路由算法无法考虑两条路由间的相互关系，无法为业务配置双路由。

按两条路径间的相互关系，公共通信网中双路由算法主要分为节点不相交算法[10-11](Node-disjoint routing algorithm, NDRA)、链路不相交算法[12-14](Link-disjoint routing algorithm, LDRA)与最大不相交算法[15](Maximally disjoint routing algorithm, MDRA)。相对于单路由算法，三种类型算法所得到的双路由均可提高业务的可靠性。但与公共通信网相比，电力通信网对业务的可靠性要求更高。因此，电力通信网中双路由算法需要进一步考虑三种双路由算法的特点，选择最适合电力通信网的双路由算法完成双路由分配工作。

鉴于现有研究的不足，本文提出一种最可靠环路策略下的最大不相交双路由算法(MRMLS)。该算法可为业务分配一组公共元素最少的双路由，且该双路由满足最可靠环路条件，这能够进一步保障双路由具有较高的可靠性。

1 电力通信网双路由问题描述

1.1 双路由算法分析

1.1.1 三种双路由算法比较

NDRA、LDRA与MDRA三种类型的双路由算法[15]并不都适用于电力通信网。除源节点与目的节点，NDRA要求两条路由绝对分离；因此，NDRA也被称为不相交双路由算法。NDRA并不适用于所有网络结构。图1为某通信网络拓扑图，考虑从A点到Z点，与B点到Z点配置节点不相交双路由，由于无法越过公共节点，两次NDRA均会失败。而在实际中，为保障业务的可靠性，可分别为两个业务分配图2(c)与图3所示的具有最少公共元素的双路由。

图1 某通信网络拓扑图

图2 链路分离双路由

一般情况下，链路故障的概率要大于节点故障概率[6]，因此，LDRA同样具有较高的可靠性。但电力通信网对业务的可靠性要求更高，LDRA得到的两条路径可能存在多个相交节点，算法在可靠性上存在缺陷。图2为从A点到Z点的三组链路分离双路由(两条路由分别用实线与虚线表示)。如果在图1中，采用LDRA从A点到Z点分配双路由，则LDRA可能得到图2(a)、图2 (b)、图2 (c)三种结果，而实际中我们更倾向于选择图2(c)中具有最少公共元素的双路由。若进一步考虑从B点到Z点分配双路由，则由于LDRA无法越过公共链路B-D，LDRA无法找到可行解。

在算法间相互的关系上，MDRA包含NDRA。MDRA可越过网络中的公共节点或公共链路，为双路由分配一组公共元素最少的双路由。若采用MDRA分别为A点到Z点，与B点到Z点的两条业务分配双路由，则MDRA可直接分配图2(c)与图3所示满足最大不相交条件的双路由。

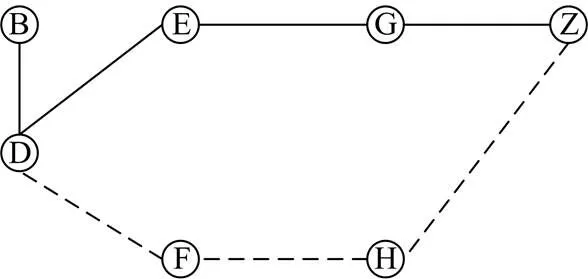
图3 最大不相交双路由

相对于NDRA，MDRA拥有更高的网络适应能力；相对于LDRA，MDRA拥有更高的网络适应能力且所得到的双路由具有更高的可靠性。因此，与其他两种算法相比，MDRA更适用于电力通信网。

1.1.2 最大不相交双路由

如图4，从A点到Z点的最大不相交双路由包含两条路由的公共部分和两条路由的分离部分。公共部分由双路由中无法避开的节点和链路组成，分离部分由多组不相交的双路由所组成。分离部分中每一组不相交双路由均可组成环路。因此，每一组最大不相交双路由均可由多组环路和其他公共节点与公共链路组成。

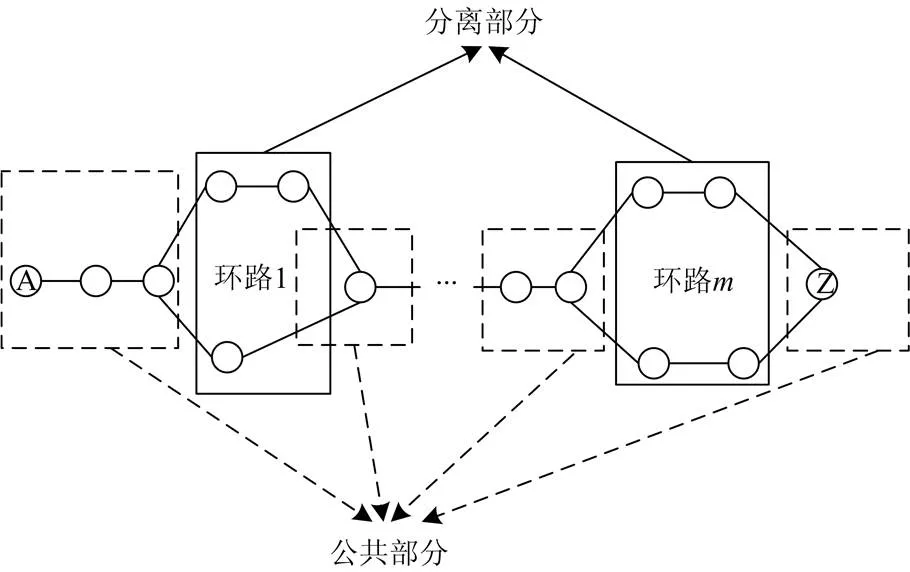
图4 最大不相交双路由的组成

最大不相交双路由必须要满足最大不相交条件，所以最大不相交双路由中所包含的任意一组不包含有任何公共节点与公共链路的不相交双路由相互独立。例如在图4所示的最大不相交双路由(此时双路由不包含双路由中的公共节点)中，环路1与环路所对应的两组不相交双路由相互独立。

1.2 最可靠环路策略

最大不相交双路由算法仅可保证所得到的双路由具有最少的公共链路与公共节点，当网络中存在多组最大不相交双路由时，采用不同的路由策略会得到不同的路由结果。

1.2.1 最可靠双路由

设为网络中的节点，为网络中的链路，()表示节点的可靠度，()表示链路的可靠度。网络中的路由P是由网络中的节点与链路所组成的串接系统[16]，路由P的可靠度可通过公式(1)计算：

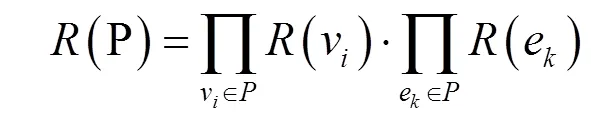
双路由的可靠度计算需要考虑两条路由间的相互关系，为简化分析，首先考虑不相交双路由情况。如图5所示，设节点A与节点Z间的主用路由为AP，备用路由为BP(AP与BP不包含公共节点A与Z)，主备用路由的可靠度分别为(AP)与(BP)。在实际中，AP与BP并不同时使用，所以两条路由组成的系统为并接系统[16]。

图5 主备用路由所组成的并接系统

Fig. 5 Parallel system based on the main route and spare route

AP与BP组成的并接系统可靠度可通过公式(2)计算：

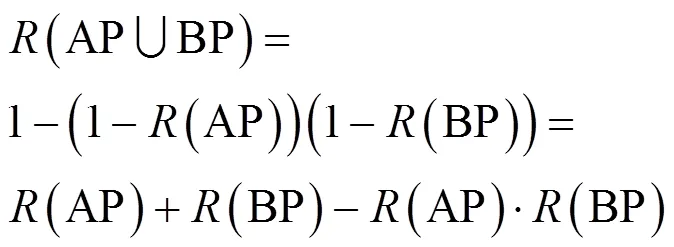
此时A、Z两点间可靠度可通过公式(3)计算：

(3)

设A点与Z点间最大不相交双路由包含组不相交双路由，第组不相交双路由的主备用路由分别为AP与BP；设A点与Z点间最大不相交双路由的公共部分可靠度为(public)。则A点到Z点间双路由的可靠度可通过公式(4)计算：

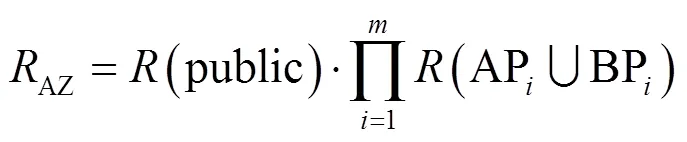
A点与Z点间所有最大不相交双路由的公共部分保持不变，且每一组最大不相交双路由所包含的多组不相交双路由相互独立。因此，A点与Z点间满足最可靠条件的最大不相交双路由需要满足公式(5)。

(5)

即当A点与Z点间最大不相交双路由所包含每一组不相交双路由可靠度均达到最大值时，此时最大不相交双路由可靠度最高。

1.2.2 最可靠环路配置方法

采用最可靠策略分配最大不相交双路由，需要保证最大不相交双路由中多组不相交双路由的可靠度均取得最大值，在实际中很难保证最大不相交双路由满足上述条件。

为便于工程实现，本文采取最可靠环路策略为业务分配最大不相交双路由。如图5所示，当不相交双路由可靠度乘积(AP)∙(BP)的值取得最大值时，此时AP与BP所组成的环路可靠性最高。

当最大不相交双路由(AP)∙(BP)取得最大值时，此时如公式(6)，最大不相交双路由所包含的每一个环路在此时均为最可靠环路，此时的最大不相交双路由即为满足最可靠环路条件的最大不相交双路由，此时的配置方法即为最可靠环路配置方法。

定义1双路由的主备用路由AP与BP可靠度乘积(AP)∙(BP)取得最大值时，此时的双路由配置方法即为最可靠环路配置方法。

相对于最可靠双路由，满足最可靠环路条件的双路由可靠性较低。但在实际中，在最大不相交的限制条件下，在相当多的时候两种分配策略的结果是一致的。当两种分配策略的结果产生差异时，满足最可靠环路条件的双路由可保证双路由中的每一个环路的可靠度均取得最大值，此时双路由同样具有较高的可靠性。

1.3 算法数学模型

本文在最大不相交双路由的条件下，采用最可靠环路策略为电力通信网分配双路由。

定义2 设P1与P2为同一网络中的两条路由，则P1与P2的相交度为P1与P2中公共节点与公共链路的数量和，其数学表示方法为(P1∩P2) (cardinality of P1∩P2，集合P1∩P2的基数，在此表示集合P1∩P2中节点与链路的数量和)。

因此本文算法可描述为在相交度最小的条件下，为源点与目的节点分配一组可靠度乘积最高的主备用路由AP与BP。本文算法的目标如公式(7)所示。

2 最大不相交双路由配置方法

MDRA的研究相对较少，一般比较直接的最大不相交双路由配置方法可通过RF(Remove-Find)算法与KSP(K-Shortest Paths)算法进行适当改进得到。改进的RF算法(Improved Remove-Find, IRF)首先找到一条最短路径，再将最短路径上节点与链路的权值修改为足够大的权值，最终再次寻找最短路径，两条最短路径即为所求最大不相交双路由。IRF算法存在所配置的双路由不一定为最大不相交双路由的缺陷。

基于KSP(K-shortest path)算法的最大不相交双路由算法(Maximally disjoint paths algorithm based on KSP, M_KSP)寻找多条源点与目的节点间的路径，通过筛选得到多组最大不相交双路由，最终配置一组可靠度最高的双路由。一般路径数量K设置的越大，得到最优解的几率就会越大。但在实际中，很难为KSP算法提前设定一个适合于本网络的路径数量值K，使M_KSP一定能得到最可靠的最大不相交双路由；采用KSP算法会产生多条冗余路径，算法效率较低；KSP算法时间复杂度较高，当路径数量K过大或网络节点数量较多时会导致M_KSP运行时间过长。

Bhandri最大不相交双路径算法[15](Maximally- disjoint paths algorithm of Bhandari version, MPAB)可为源点与目的节点分配一组路径权值和最小且满足最大不相交条件的双路由。MPAB不存在理论缺陷，可在任意网络中为任意节点对分配权值和最小的最大不相交双路由。本文的路由算法是基于MPAB算法的改进算法，改进后的算法可为业务分配满足最可靠环路条件的最大不相交双路由。

2.1 Bhandari最大不相交算法

图6为MPAB在为A点到Z点分配最大不相交双路由过程中的网络拓扑变化示意图。其中，图6(a)为某通信网网络拓扑图；图6(b)为采用基于最短路径的节点分裂方法对图6(a)进行网络拓扑修改所得到的网络拓扑图；图6(c)为MPAB将运算过程中产生的两条路径进行组合所产生的网络拓扑图；图6(d)为MPAB利用相关运算结果，对图6(c)所示网络进行网络权值修改所得到的网络拓扑图。结合图6，MPAB的运算过程描述如下。

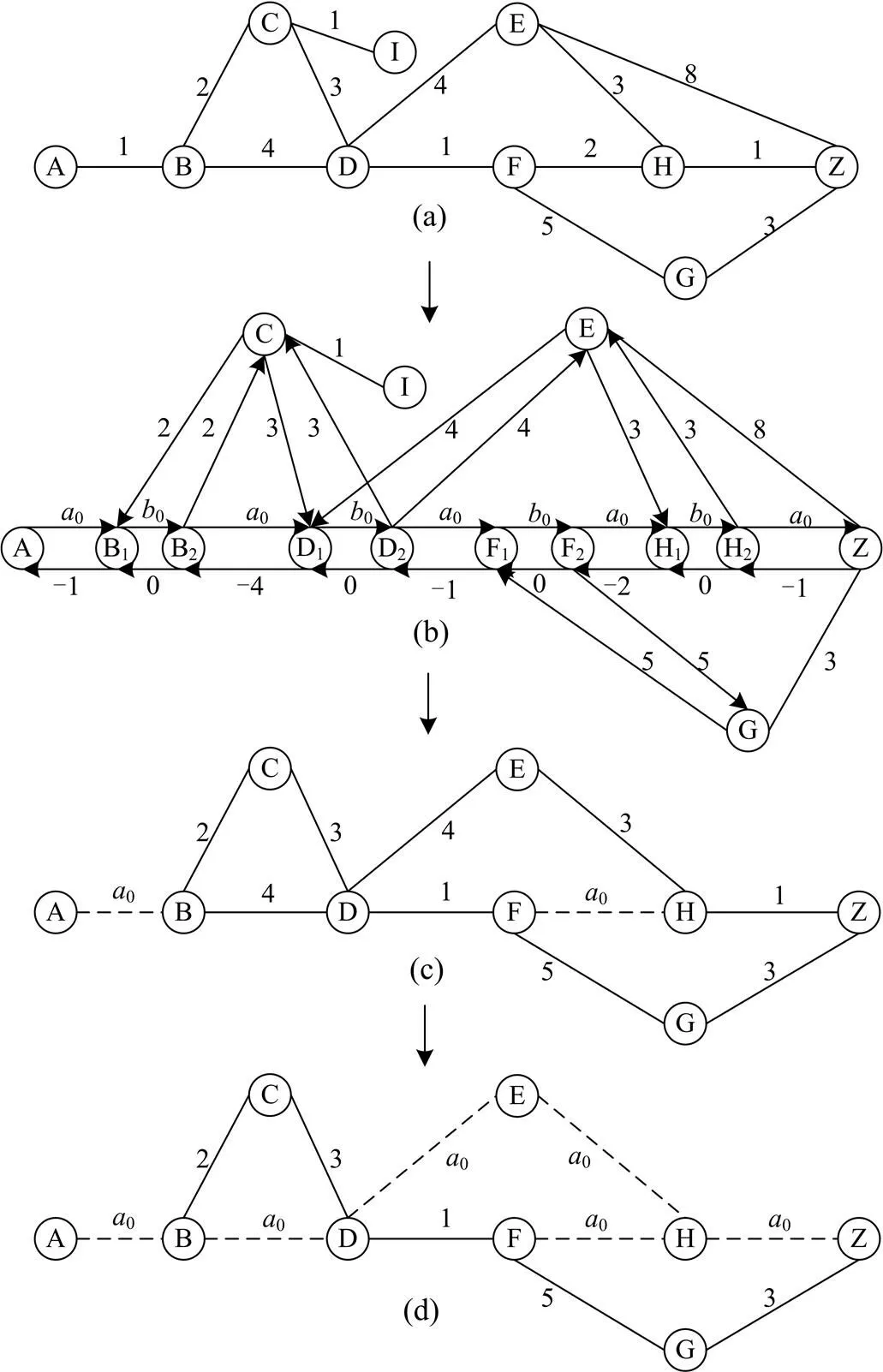
图6 MPAB中网络拓扑的变化

第一步，在图6(a)网络中，调用改进的Dijkstra算法，得到最短路径path1(A-B-D-F-H-Z)。

第二步，采用基于最短路径的节点分裂法修改网络中相应边与点的连接关系以及它们的权值，得到新的网络拓扑如图6(b)所示。

基于最短路径的节点分裂方法具体为：规定路径中由源点到目的节点的方向为正向，其相反方向为反向；path1路径上除去起点和终点外的其他点一分为二，如B分裂为B1与B2，B1与B2间反向边的权值为0，正向边的权值设置为0；path1中所有链路反向权值变为原链路权值的相反数，链路正向权值置为0；非path1路径上的节点(以C为例)如果之前与该路径有连接关系，那么将C以单向边连到B1与B2；单向边在方向上满足边C→B1、B2→C与B1→B2组成单向环路，边C→B1、B2→C权值仍为原来双向边BC的权值。设图6(a)中的网络为，(e)为链路的权值，n应大于最终得到的主备用路由所包含的公共链路数(n可设置为path1所包含的链路数)，则0与0满足公式(8)：

第三步，在图6(b)网络中，调用改进的Dijkstra算法，得到路径path2(A-B1-B2-C-D1-D2-E-H1-F2-G- Z)，将path2中分裂节点还原为原节点，此时path2变为A-B-C-D-E-H-F-G-Z。

第四步，并将path1与path2组成一个简单网络如图6(c)所示，path1与path2所重合得链路权值设置为0，如虚线所示，在图5(c)中执行改进的Dijkstra算法，得到AP(A-B-D-E-H-Z)。

第五步，在图6(c)中将AP所包含的链路权值修改为0，得到图6(d)所示网络，调用改进的Dijkstra算法，得到BP(A-B-C-D-F-G-Z)。

2.2 满足最可靠环路条件的双路由算法

为解决电力通信网双路由分配问题，本文将MPAB进行改进，提出一种最可靠环路策略下的最大不相交双路由算法(the Maximally Disjoint Routing Algorithm Under the Most Reliable Loop Strategy，MRMLS)。相对于MPAB，MRMLS 有以下4个方面的改进之处：

(1) MPAB在计算过程中没有考虑到网络中的节点权值，应用到电力通信网中应进一步考虑网络中的节点权值；

(2) 电力通信网注重业务的可靠性，双路由算法应从可靠性出发，为电力通信业务分配可靠性的双路由；

(3) MPAB在计算过程中会对网络的权值进行修改，算法得到的主备用路由AP与BP的权值为伪权值，最终应再次计算AP与BP的真正路径权值与此时的双路由的可靠度；

(4) 为直接反映双路由的相互关联情况并反映源点与目的节点间网络拓扑的连接状况，应计算MPAB所得主备用路由的相交度。

2.2.1 考虑节点权值的双路由算法

MPAB没有考虑到网络中的节点权值，可将MPAB中改进的Dijkstra算法进行修改[2]，使其进一步考虑节点权。但单纯考虑节点权值的改进型Dijkstra算法很可能会导致MPAB在路径搜索中出现错误。例如在图7中，为1号节点到5号节点分配双路由，采用考虑节点权值的MPAB算法会得到1-6-7-4-5与1-2-3-8-9-5两条路由，其权值和为49。而实际中权值和最小的双路由为1-6-7-4-5与1-2-10-11-5，其权值和为42。这是因为在节点分裂的网络中，若从节点3到节点2，需要两次经过3号节点，导致3号节点的权值叠加两次，使MPAB产生错误解。

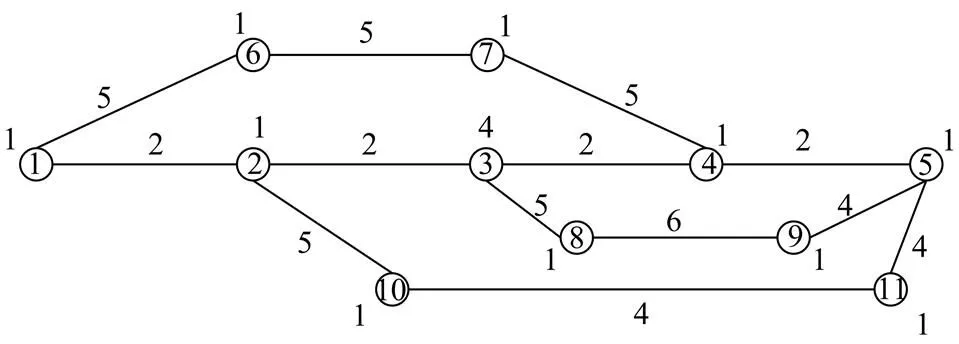
图7 带有节点权值的网络拓扑图

在节点分裂的网络中不能简单叠加节点权值， Dijkstra算法需要进一步识别路径是否已经抵达此节点。若Dijkstra算法已经抵达此节点，则再次经过此节点时，此节点的权值变为0。

MPAB在计算过程中加入了节点权值，为排除节点权值对路径搜索结果产生的影响，应按公式(9)调整0与0的大小。

2.2.2 最可靠环路双路由算法

MPAB算法仅可采用链路的加性权值进行双路由搜索，不能计算节点与链路的可靠度乘积。链路与节点的可靠度分布在(0, 1)区间，可通过取负对数的方法，将可靠度由乘性参数变为加性参数。此时的MPAB算法得到的AP权值(AP)与BP权值(BP)的和满足公式(10)：

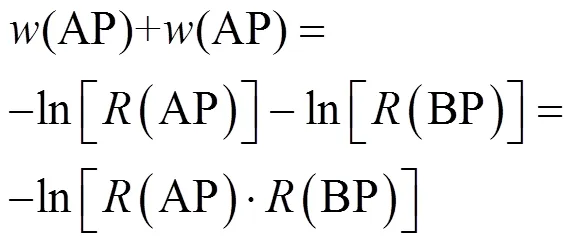
MPAB算法得到的两条最大不相交路径的权值和(AP)(BP)最小，通过公式(10)可进一步得到此时两条路由AP与BP的可靠度乘积(AP)∙(BP)最大。即此时MPAB算法得到的两条最大不相交双路由为满足最可靠环路条件的双路由。

2.2.3 双路由相交度与业务可靠度

最大不相交双路由中的公共元素越多，两条路由同时出现故障的概率就会越大。因此，可通过计算最大不相交双路由的相交度(APBP)，直接反映此时主备用路由同时失效的风险。

源节点与目的节点间双路由的最大不相交度由两个点间的网络连接状况所决定，因此可通过最大不相交双路由的相交度可为进一步分析源节点与目的节点间网络的连接状况。

为准确反映采用当前最大不相交双路由的可靠性，需要通过AP与BP按公式(4)重新计算此时最大不相交双路由的可靠度。

2.2.4 MRMLS的算法流程

本文通过修改MPAB得到MRMLS，图8为MRMLS的算法流程图，MRMLS具体步骤为：

图8 MRMLS算法流程图

(1) 将网络中节点与链路的可靠度取负对数，得到算法网络；

(2) 获取当前配置业务的源点(s)与目的节点(t)；

(3) 采用考虑节点权值的MPAB在源点与目的节点间寻找最大不相交双路径；

(4) 分别计算两条路径的可靠度，并将可靠度较高的路径配置为主用路由AP，另一条配置为备用路由BP；

(5) 计算当前双路由的相交度st；

(6) 计算采用AP与 BP的最大不相交双路由的可靠度；

(7) 判断是否有剩余业务，若有剩余业务则返回步骤(2)，若无剩余业务，则算法结束。

设网络中的节点数量为，链路数量为，网络中路径的平均节点数为，则运行一次MRMLS的时间复杂度为O(∙log()log()4∙log (2)22)。

3 算法仿真分析

MDRA的研究相对较少，本文采取两种比较直接的方法IRF与M_KSP算法作为本文所提出的MRMLS的对比算法。其中M_KSP分别采取路径数量为50、100与500的M_50SP、M_100SP与M_500SP算法进行仿真。

图9为我国某地区电力通信网网络拓扑图，其包含101个节点，141条链路。在图9中，链路可靠度在[0.99, 0.999]间自动生成，节点可靠度在[0.999, 0.9999]间自动生成，分别采用上述方法为网络中任意节点对之间分配一组最大不相交双路由(总业务数量为5 050条)，则对比结果如下。

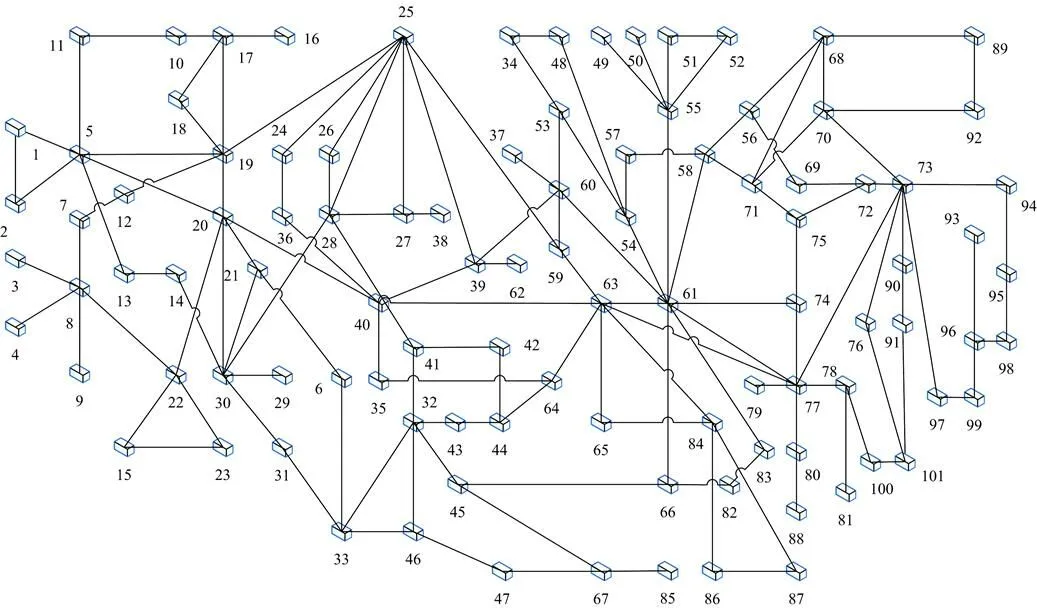
图9 我国某地区电力通信网网络拓扑图

3.1 双路由相交度

在双路由的配置过程中， MRMLS所得到的每一组双路由均具有最小相交度，这进一步验证了MRMLS为最大不相交双路由算法。IRF与M_KSP并不能保证其所配置双路由具有最小相交度。在部分业务的配置过程中，相对于最大不相交双路由，两种算法得到的双路由相交度会变大。

表1展示了在不同算法、不同相交度下，双路由的数量分布。从表1中可以看出，MRMLS在各个相交度的双路由数量均大于等于其他几种算法；随着相交度的增大，其他几种算法的双路由数量会逐渐接近MRMLS；但在相交度较小的区域，其他算法与MRMLS有较大差距。

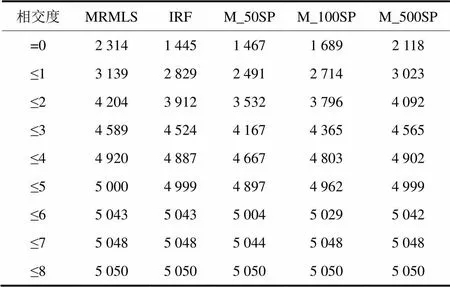
表1 不同相交度下的双路由数量分布表

为突出数据的变化趋势，方便其他算法与MRMLS进行对比，本文采用MRMLS列数据对其他4列数据进行归一化，得到图10所示的双路由相交度变化曲线。

图10 双路由数量随双路由中公共元素数量的变化情况

从图10中可看出，IRF的双路由相交度曲线低于要 MRMLS与M_500SP；M_KSP随着路径数量的增加，其相交度会逐渐接近MRMLS；但与MRMLS相比，即使是采用路径数量较多的M_500SP，二者在相交度上依然有较大差距。因此，与IRF、M_KSP相比，MRMLS所得到的双路由公共元素最少，双路由同时故障的几率更小，在可靠性上MRMLS具有显著优势。

3.2 路由可靠度

IRF不能保证所得到的双路由为最可靠双路由。M_KSP通过筛选多条源点目的节点间路径，得到相交度最小的最可靠双路由；在任意网络中，当M_KSP的路径数量上限K→∞时，M_KSP所得到的双路由即为相交度最小且可靠性最高的双路由。在实际中，M_KSP很难得到源节点到目的节点的所有路径。在本次仿真中，M_500SP的路径数量远远高于网络中节点数量与链路数量，本文采用M_500SP来近似估测最可靠的最大不相交双路由。

本文采取MRMLS、M_500SP、与最可靠单路由(Most Reliable Single Route, MRSR，可通过KSP筛选得到)进行对比。相交度的变化会对双路由的可靠性产生影响，因此，在进行可靠性分析时需要保证MRMLS与M_500SP所得到的双路由具有相同的相交度。在5 050条业务中，MRMLS与M_500SP具有相同相交度的业务共有4 628条。为便于人眼分析，将三组数据按M_500SP的可靠度进行升序排序，得到图11所示曲线图。

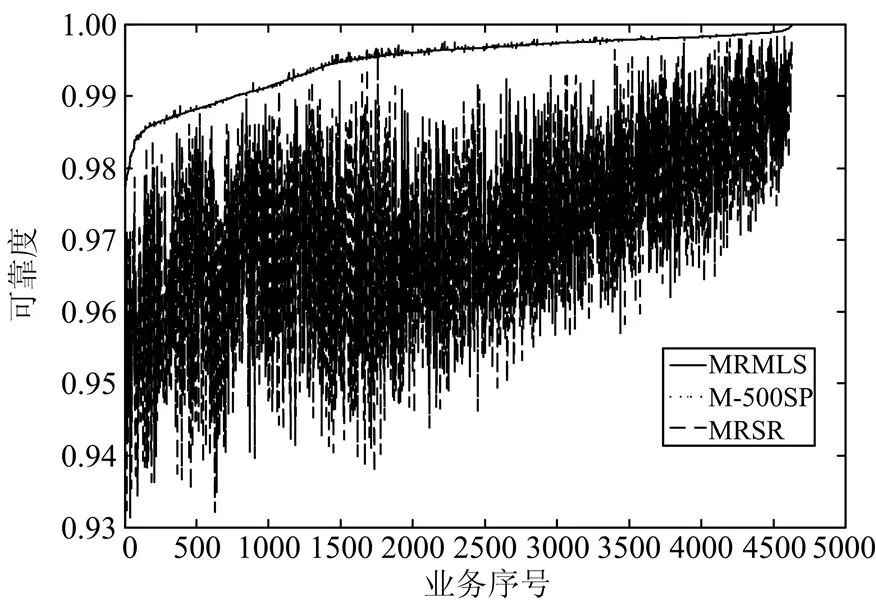
图11 路由可靠度比较

图11中，M_500SP对应的可靠度曲线为图11中顶部的一条平滑曲线；MRMLS的曲线与M_500SP的曲线近似重合；MRMLS与 M_500SP所得到的双路由可靠度均远高于最可靠单路由(MRSR)的可靠度。由此可见，最大不相交双路由的可靠性要优于最可靠单路由的可靠性。

进一步求三种算法的可靠度的平均值，MRMLS、M_500SP与MRSR的可靠度平均值分别为0.994 575、0.994 569与0.971 184。MRMLS所得到的双路由可靠度平均值要略微高于M_500SP。若想进一步提高M_500SP得到的双路由可靠度，需要进一步提高M_500SP的路径数量。因此，相对于最可靠单路由MRSR与M_500SP，MRMLS得到的最大不相交双路由具有更高的可靠性。

3.3 路由跳数分析

路由的跳数越多，其所占用的节点与链路的资源量就会越大，其完成相应工作的效率就会越低。若算法单纯从最可靠环路或最可靠双路由角度出发，可能会造成双路由的跳数和(两条路由的节点数之和)过大。为分析双路由所占用的网络资源量，在MRMLS与M_500SP所得的双路由具有相同相交度的情况下，本文采取MRMLS与M_500SP两种算法的双路由结果与跳数和最少的最大不相交双路由(The Maximally Disjoint Routes with Least Hops, MDRLH，可通过KSP筛选得到)作对比，分析三种双路由的跳数和的分布情况。

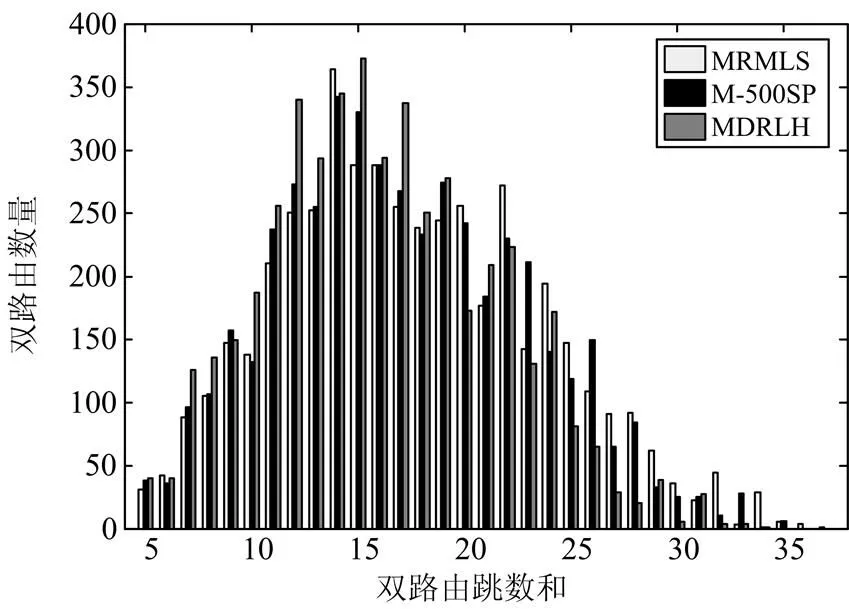
图12 不同路由策略下的双路由跳数和

从图12中可以看出，三种路由策略下的双路由跳数和的分布区间与变化趋势大体一致。进一步求双路由跳数和的平均值，得到MRMLS、M_500SP与MDRLH的跳数和平均值分别为19.01、18.6、17.42。相对于MDRLH，在路由跳数和上MRMLS与M_500SP分别提高了9.1%与6.8%。这说明不同路由策略下的双路由跳数和变化并不明显，MRMLS得到的双路由并不会占用过多的网络资源。

3.4 算法时间复杂度分析

本文采用2.6 GHz四核心处理器，4 GB内存， WIN7系统的主机对算法进行仿真；仿真软件为VS2010，采用C++语言实现五种算法。本文的M_KSP算法采用的KSP算法为删除路径算法。

为分析五种算法的运行时间，本文选取节点数量为100, 200, … , 800且链路数量为节点数量1.6倍的网络进行仿真；在每个网络中随机选取100条业务，分别采用五种算法为业务分配双路由；在不同节点数量的网络中，分别计算不同算法的平均运行时间。

五种算法的平均运行时间随节点数量变化的曲线如图13(a)所示；为了进一步清晰显示图13(a)中轴附近的曲线，将图13(a)中M_100SP与M_500SP所对应的曲线删去，并将图13(a)进行放大，得到图13(b)所示曲线图。

从图13(a)中可以看出三种M_KSP算法的平均运行时间均高于IRF与MRMLS，且M_KSP曲线更为陡峭，若节点数量进一步增加，则M_KSP与IRF、MRMLS的运行时间差会进一步增加。

进一步地，图13(b)中IRF的平均运行时间要略小于MRMLS；MRMLS与IRF的运行时间要远小于M_50SP的运行时间。

在上文所述我国某地区电力通信网中(对应于节点数量为100的网络)，采用MRMLS、IRF、M_50SP、M_100SP与M_500SP分别为5 050条业务分配双路由的时间分别为17.51 s、6.32 s、1 598.3 s、1.05 h与8.5 h。

IRF的平均运行时间最短，但得到满足最大不相交条件的双路由数量较少；而算法效果相对较好的M_KSP的运行时间较长，当路径数量与网络节点数量增多时，其运行时间会大幅增加，且M_KSP同样很难保证其所得到的双路由为最大不相交双路由。

因此， MRMLS不仅在算法效果上要优于其他几种算法，同时MRMLS也拥有较小的时间开销。

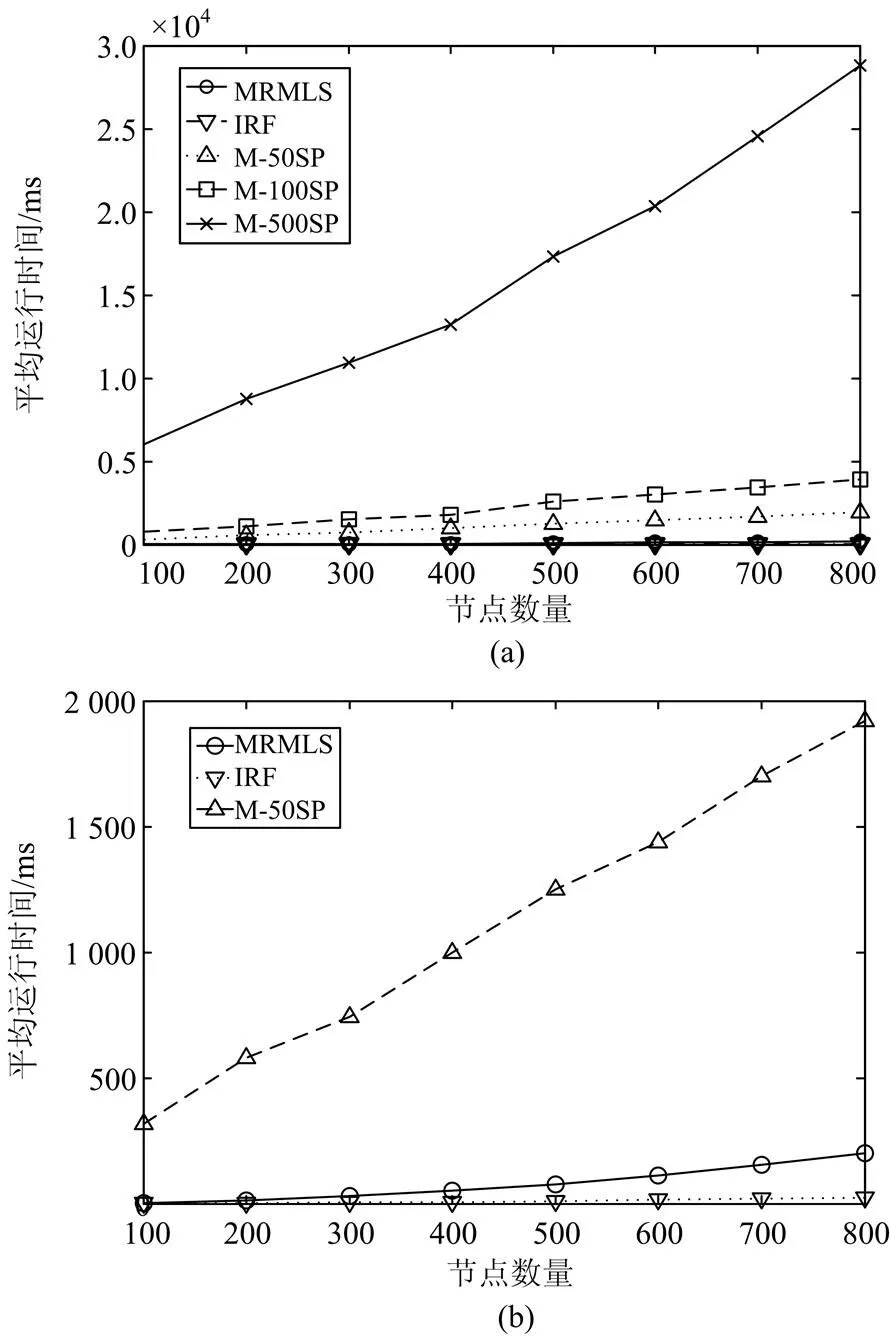
图13 算法运行时间比较

4 结束语

针对电力通信网的双路由分配问题，本文提出一种最可靠环路策略下的最大不相交双路由算法(MRMLS)。该算法可为业务分配一组公共元素最少的双路由，且该双路由满足最可靠环路条件，这能够进一步提高双路由的可靠性。仿真结果表明，MRMLS具有较小的时间开销，并可保证所得到的双路由具有较高的可靠性。

[1] 金鑫. 高压直流输电系统极控信号通信网络可靠性分析[J]. 电力系统保护与控制, 2015, 43(12): 110-116.

JIN Xin. Reliability analysis on HVDC pole control signal transmission network[J]. Power System Protection and Control, 2015, 43(12): 110-116.

[2] 高会生, 王慧芳. 基于安全性的继电保护光纤迂回通道路径选择[J]. 电力系统保护与控制, 2014, 42(14): 25-31.

GAO Huisheng, WANG Huifang.Path selection based on security measure for relay protection services of fiber circuitous channel[J]. Power System Protection and Control, 2014, 42(14): 25-31.

[3] 倪明放, 王曦, 武欣嵘, 等. 多约束最优路由选择和不相交路由选择问题[J]. 军事通信技术, 2010, 31(4): 71-76.

NI Mingfang, WANG Xi, WU Xinrong, et al. Multi- constrained optimal path selection and disjoint path selection[J]. Journal of Military Communications Technology, 2010, 31(4): 71-76.

[4] 吴润泽, 祁宏鹏, 唐良瑞. 新一代电力ICT网络中基于DiR保护环的生存性路由算法[J]. 电力系统保护与控制, 2011, 39(16): 25-29.

WU Runze, QI Hongpeng, TANG Liangrui. Survival routing algorithm based on DiR protection ring in novel power ICT network[J]. Power System Protection and Control, 2011, 39(16): 25-29.

[5] 曾庆涛, 邱雪松, 郭少勇, 等. 电力通信业务路由分配算法[J]. 北京邮电大学学报, 2013, 36(3): 79-82, 87.

ZENG Qingtao, QIU Xuesong, GUO Shaoyong, et al. Routing algorithm for power communications service assignment[J]. Journal of Beijing University of Posts and Telecommunications, 2013, 36(3): 79-82, 87.

[6] 蔡伟, 杨洪, 熊飞, 等. 考虑电力通信网可靠性的业务路由优化分配方法[J]. 电网技术, 2013, 37(12): 3541-3545.

CAI Wei, YANG Hong, XIONG Fei, et al.An optimized service routing allocation method for electric power communication network considering reliability[J]. Power System Technology, 2013, 37(12): 3541-3545.

[7] 曾瑛, 蒋康明, 杨娇, 等. 基于量子遗传算法的电力通信网路由选择策略[J]. 太原理工大学学报, 2013, 44(4): 501-505.

ZENG Ying, JIANG Kangming, YANG Jiao, et al. Power communication network routing selection strategy based on quantum genetic algorithm[J]. Journal of Taiyuan University of Technology, 2013, 44(4): 501-505.

[8] 张铭泉, 胥鸣, 秦文韬. 基于改进粒子群算法的电力通信网最佳抢修路径问题的研究[J]. 科学技术与工程, 2008, 22(8): 5990-5995.

ZHANG Mingquan, XU Ming, QIN Wentao.Research of the best repair path based on an improved particle swarm optimization in power communication network[J]. Science Technology and Engineering, 2008, 22(8): 5990- 5995.

[9] 曾瑛, 李伟坚, 陈媛媛, 等. 基于业务优先级的电力调度数据网拥塞规避算法[J]. 电力系统保护与控制, 2014, 42(2): 49-55.

ZENG Ying, LI Weijian, CHEN Yuanyuan, et al.A congestion avoidance algorithm based on the service priority for electric power dispatching data network[J]. Power System Protection and Control, 2014, 42(2): 49-55.

[10] SUURBALLE J W. Disjoint paths in a network[J]. Networks, 1974, 4(2): 125-145.

[11] BHANDARI R. Optimal diverse routing in telecommunication fiber networks[C] // INFOCOM'94. Networking for Global Communications, 13th Proceedings IEEE: IEEE, 1994: 1498-1508.

[12]张品, 张坚武, 李乐民, 等. QoS约束下的链路分离问题的研究[J]. 通信学报, 2006, 27(6): 37-42.

ZHANG Pin, ZHANG Jianwu, LI Lemin, et al. Researches on the problem of link disjoint paths pair with QoS constraints[J]. Journal on Communications, 2006, 27(6): 37-42.

[13]熊轲, 裘正定, 郭宇春, 等. 多约束最短链路分离路径精确算法[J]. 软件学报, 2010, 21(7): 1744-1757.

XIONG Ke, QIU Zhengding, GUO Yuchun, et al.Exact algorithm for multi-constrained shortest link-disjoint paths[J]. Journal of Software, 2010, 21(7): 1744-1757.

[14]倪明放, 高石云, 武欣嵘, 等. 求不相交QoS路由的一种整数线性规划方法[J]. 控制与决策, 2012, 27(10): 1597-1600.

NI Mingfang, GAO Shiyun, WU Xinrong, et al. Integer linear program method of finding link-disjoint paths for QoS routing[J].Control and Decision, 2012, 27(10): 1597-1600.

[15]BHANDARI R. Physical diversity versus cost algorithm for networks[J]. Simulation Series, 1996, 28: 258-264.

[16]周炯槃, 张琳, 望育梅, 等. 通信网理论基础[M]. 北京: 人民邮电出版社, 2009: 166-187.

(编辑 周金梅)

A maximally disjoint routing algorithm for power communication networks

HE Yujun, CHEN Ran, ZHANG Wenzheng, LIU Yi, ZHOU Shengping

(Dept of Electronics and Communication Engineering, North China Electric Power University, Baoding 071000, China)

Since the existing routing algorithms for power communication network could not be used for finding a pair of routes, the maximally disjoint routing algorithm under the most reliable loop strategy (MRMLS) is proposed. Three types of double routing algorithms for the public communication network are discussed. Considering the diversity of the network topology, the maximally disjoint routing algorithm is adopted. The reliability of maximally disjoint routes is studied, and the maximally disjoint routes with the characteristic of the most reliable loop are put to use. The original maximally disjoint routing algorithm is improved, and the reliability of nodes and links is considered in the proposed algorithm. Simulation experiment compares MRMLS with another two available routing algorithms. The experiment results show the feasibility and validity of MRMLS. This work is supported by Fundamental Research Funds for the Central Universities (No. 13MS64).

power communication network; double routes; maximally disjoint; reliability; the most reliable loop

10.7667/PSPC150818

中央高校基本科研业务费专项资金资助(13MS64)

2015-05-14；

2015-07-09

何玉钧(1974-)，男，副教授，硕士生导师，研究领域为电力通信网管理、安全风险评估； 陈 冉(1989-)，男，通信作者，硕士研究生，主要研究方向为电力通信业务路由配置方法；E-mail: crncepu@163.com 张文正(1990-)，男，硕士研究生，主要研究方向为电力通信网通信资源管理。