夏季日最大降温负荷的估算和预测方法

刘思捷，张海鹏，林舜江，刘明波，李嘉龙，王 一，孙 谦



夏季日最大降温负荷的估算和预测方法

刘思捷1，张海鹏2，林舜江2，刘明波2，李嘉龙1，王 一1，孙 谦1

(1.广东电网公司电力调度控制中心，广东 广州 510600；2.华南理工大学电力学院，广东 广州 510640)

随着空调等降温设备的大量使用，降温负荷对电力系统安全经济运行的影响越来越显著。以广州市的历史负荷和气温数据为基础，分析了广州市夏季降温负荷与气温之间相关性。首先，考虑到夏季基准负荷逐日的增长量，提出利用灰色系统GM(1,1)模型预测出电网夏季的日基准负荷曲线，进而准确剥离出夏季的日降温负荷曲线，并分析了日降温负荷曲线的“W”型变化特征。其次，基于日最大降温负荷与日最高温度的相关性分析，建立了日最大降温负荷与日最高温度之间关系的分段回归模型，并对日最大降温负荷进行预测。最后考虑温度累积效应的影响，对分段回归模型进行了修正，进一步提高了预测精度，从而为准确预测电网夏季日高峰负荷提供依据。

降温负荷；GM(1,1)模型；相关性分析；分段回归模型；温度累积效应

0 引言

短期负荷预测是电力系统运行调度的基础，对电力系统的安全经济运行有着重要作用[1-6]。地区电网负荷变化受到多种因素的影响，如地区经济发展水平、产业结构、电价结构、气象因素、人们的用电习惯等，准确预测的难度很大。而近年来随着人们生活水平的提高，以空调为主的夏季降温负荷在地区电网负荷中的比重越来越大，气象因素对夏季短期负荷变化的影响日益突出。气象的变化直接影响到大量降温负荷设备的启停，气象突然变化引起降温负荷的快速变化已成为影响电力供求平衡的重要因素。为确保电网的安全稳定运行，提高能源的利用效率，对降温负荷与气象因素的相关性开展研究具有十分重要的意义[7]。

随着气象部门预测手段的完善和技术的发展，近几年越来越多文献通过建立数学模型对气象因素与电力负荷之间的相关性进行研究，并考虑气象因素以提高短期负荷预测精度[8-9]。显然，负荷中受气象因素影响的主要是一些如空调、风扇等气象敏感的降温负荷，为更准确地分析负荷变化与气象因素之间的相关性，从日负荷曲线中准确剥离出降温负荷尤为重要。文献[10]分析重庆电网空调降温负荷特性时采用最大负荷比较法估算日最大降温负荷，将有降温负荷日的最大负荷与无降温负荷日的最大负荷相减来确定日最大降温负荷；文献[11]则采用基准负荷比较法来剥离出降温负荷，以春季和秋季工作日负荷曲线的平均值作为基准负荷曲线，然后用夏季工作日负荷曲线减去基准负荷曲线来得到日降温负荷曲线；文献[12-13]也是采用基准负荷比较法进行降温负荷剥离，并分析了气象因素对日最大降温负荷的影响。然而，最大负荷比较法和基准负荷比较法都是对整个夏季的每一天采用同一个基准负荷值或基准负荷曲线，明显忽略了基准负荷的逐日增长量，对于电网负荷较大、经济发展较快的地区，这种做法估算出降温负荷的准确度还有待提高。

而对于降温负荷的短期预测方法，与短期负荷预测方法基本相同，包括回归法、灰色系统模型预测法和神经网络预测法等。文献[14]定义了经济因子及电能消费倾向因子，并对一元回归模型进行修正来进行日最大降温负荷预测；文献[15]建立了气象突变判断准则，并在灰色预测模型基础上进行气象因素矫正，提高模型的预测精度；文献[12]采用滤波法对气象敏感负荷数据进行处理后，以实时气象因素为输入变量，利用神经网络对气象敏感负荷进行了预测。回归法获得的日降温负荷与气温之间具有明确的函数关系式，能够回答电网运行人员关心的“温度每变化一度，降温负荷变化多少”问题，对实际电网运行调度具有更强的指导价值。

本文以广州市2008~2012年的历史负荷和气温数据为基础，提出了考虑基准负荷逐日增长量的夏季日基准负荷曲线预测模型，以准确剥离出夏季日降温负荷曲线；基于分段回归模型，获得日最大降温负荷与日最高温度之间的函数关系，进而对日最大降温负荷进行预测；并结合温度累积效应修正公式，提高了日最大降温负荷的预测精度，从而为电网“迎峰度夏”和安全经济运行提供了决策依据。

1  降温负荷的剥离

1.1 常用降温负荷剥离方法及存在问题

由于电网负荷中空调等降温负荷占比的持续增长，电网日最大负荷与气温之间的相关性越来越大。例如，广州市2009~2012年的日最大负荷变化如图1所示。可以看出：在炎热的夏季5~9月，日最大负荷值明显大于温度较低的其他月份，日最大负荷变化与气温变化之间的相关性非常明显，定量分析最大负荷变化与气温变化之间的关系尤为必要。

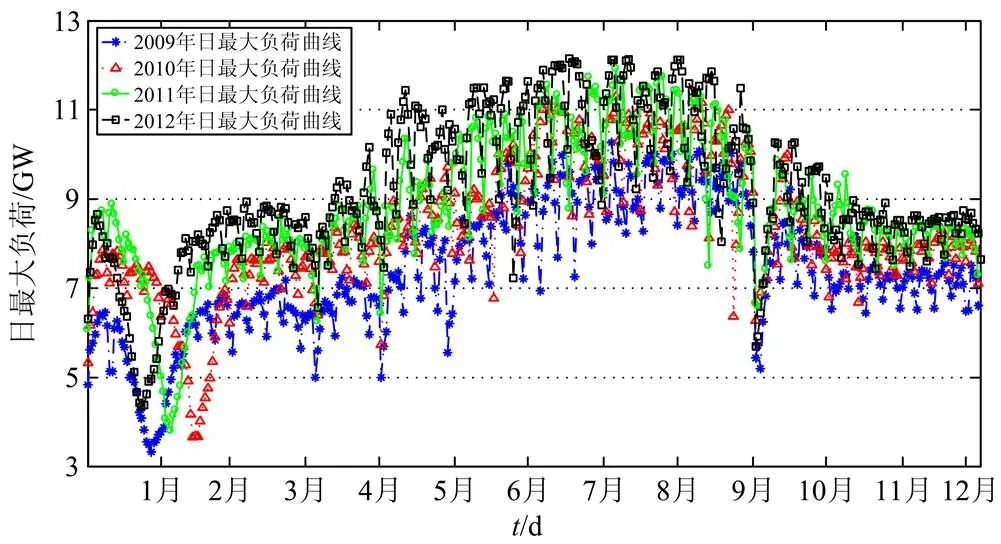
图1广州市2009~2012年日最大负荷变化

要分析降温负荷的变化特性及其影响因素，必须先从日负荷曲线中准确剥离出降温负荷。对于夏季日最大降温负荷，通常采用最大负荷比较法进行剥离[10]，然而，最大负荷比较法存在如下的问题：

(1) 没有考虑同一年夏季中每一天的基准负荷的变化，以春秋季日最大负荷的平均值作为夏季每一天的基准负荷明显不合理；

(2) 由于夏季日最大负荷与春秋季节的日最大负荷往往不在一天中同一时刻出现，因而以夏季日最大负荷与春秋季日最大负荷平均值直接相减作为夏季日最大降温负荷也明显不合理。

图2展示了广州市2009年各季节的典型日负荷曲线，可以看出：广州市日最大负荷值出现的时刻受季节影响较大，这主要是因为第三产业的比重较大。对广州市2009~2012年的负荷数据统计可知，春季负荷峰值出现在18:30~19:30之间的平均概率为52.8%，夏季负荷峰值出现在11:00~12:00之间的平均概率为96.1%，秋季负荷峰值出现在11:00~12:00之间的平均概率为64.0%，冬季负荷峰值出现在18:30~19:30之间的平均概率为75.1%。由于夏季日负荷峰值与春秋季节的日负荷峰值不一定在同一时刻出现，因此以夏季日最大负荷与春秋季节日最大负荷平均值的差值作为夏季日最大降温负荷的做法是不合理的。

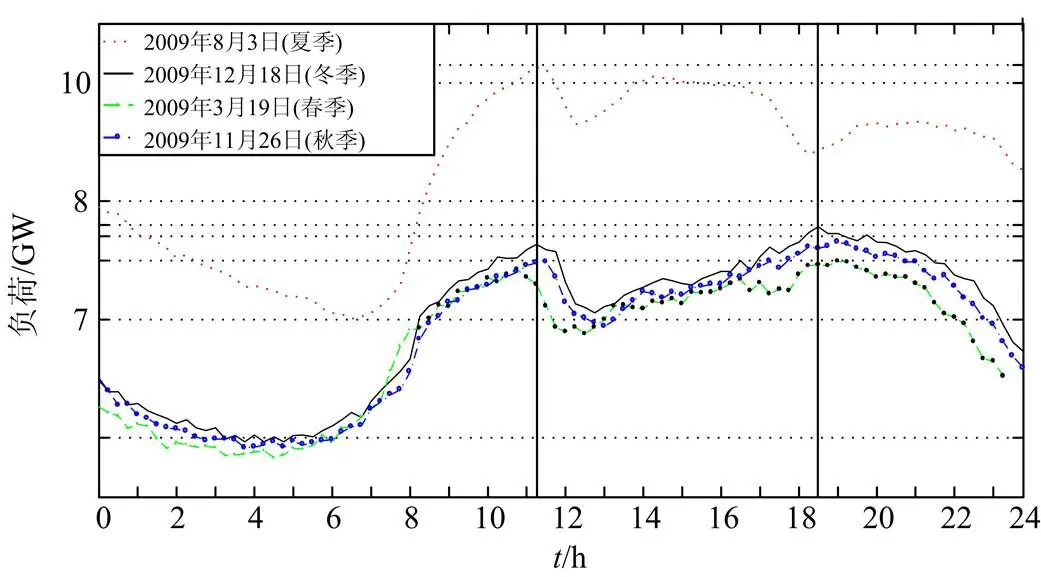
图2 广州市 2009年典型日负荷曲线

1.2 基于日基准负荷曲线预测的降温负荷剥离方法

1.2.1 基准负荷预测

电力负荷中每天同一时刻的基准负荷是具有稳定发展趋势的时间序列，与经济发展、用电结构等密切相关。为了准确地剥离出夏季工作日的降温负荷曲线，同时考虑到基准负荷具有增长性和周期性，本文以广州市2008年~2012年的历史负荷和气象数据为依据，以无降温负荷日的负荷曲线为基础采用一阶一元灰色系统模型GM(1,1)预测出广州市2012年夏季每个工作日的基准负荷曲线。

GM(1,1)模型预测的原理可参见文献[16-17]。通过对广州市2009~2012年的历史负荷数据和气象数据进行分析可知：广州市夏季持续时间长，4月下旬气温开始逐渐上升，7~8月份气温最高，而9月下旬气温开始逐渐下降，10月下旬以后几乎无降温负荷。为了准确预测出夏季日基准负荷曲线，避免降温负荷以及节假日的影响，选用待预测年春季(元宵节后~4月10日)和前一年秋冬季节(11月1日~春节前10天)的日负荷曲线数据当作不含有降温负荷，也就是GM(1,1)模型的原始数据，对待预测年夏季的日基准负荷曲线进行预测。例如，预测2009年6月~8月工作日的基准负荷曲线时，选取2008年11月1日~2009年1月16日(2009年1月26日为春节)和2009年2月10日~2009年4月10日的工作日负荷数据，剔除个别日最高温度高于27℃的工作日数据后作为GM(1,1)模型的原始数据。根据该方法，利用GM(1,1)模型预测出广州市2009~2012年夏季每个工作日的基准负荷曲线，2012年夏季部分工作日的基准负荷曲线如图3。

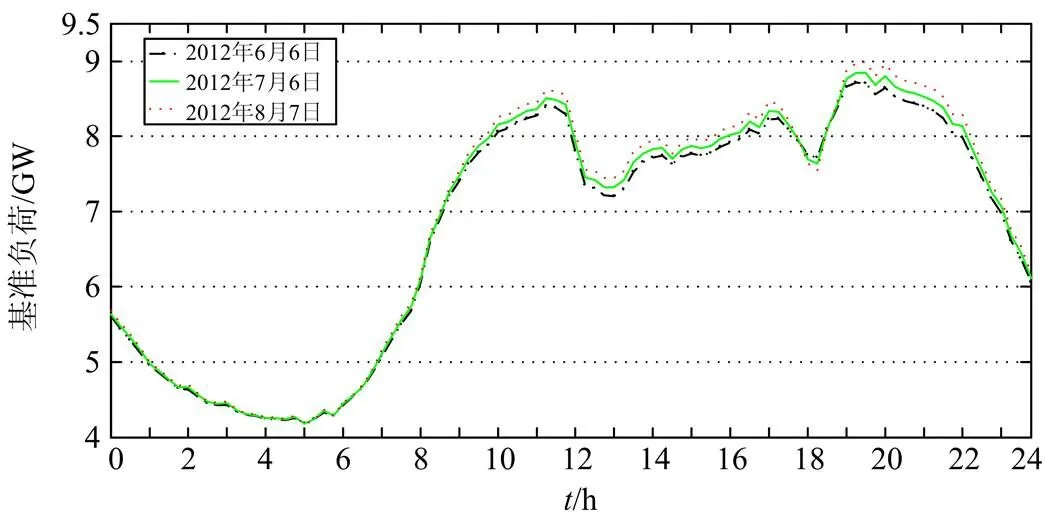
图3 2012年夏季部分工作日的基准负荷曲线

由图3可以看出，基准负荷曲线与总负荷曲线的变化趋势相似，基准负荷曲线峰值在19:00左右出现，且峰值大小随时间具有稳定的增长趋势。

1.2.2 降温负荷的剥离和估算

在获得2009~2012年夏季每个工作日的基准负荷曲线后，夏季每个工作日的96点降温负荷曲线可由日负荷曲线减去当天的基准负荷曲线得到。图4为2012年部分工作日的降温负荷曲线，可以看出，日降温负荷曲线大体上呈现出“W”型变化趋势，一天中有两个峰值，分别出现在14:30和24:00附近，而7:30和19:00左右的降温负荷出现两个低谷值。这与广州市的负荷构成、气象变化以及人们的生活习惯等密切相关。对于城市居民而言，早上7:00左右起床后会有关闭空调、自然通风的习惯，因而降温负荷较小；8:00之后随着人们陆续开始上班，降温负荷逐渐增大，夏季的日最高温度一般出现在14:00~15:00，因而降温负荷在14:30左右达到最大值；而18:00~20:00是下班的高峰期，降温负荷较小，20:00之后居民用户使用空调量开始增大，降温负荷也随之上升。特别是在22:00之后人们逐渐开始睡觉并打开空调进行房间制冷，降温负荷增长较快，并在24:00左右到达又一个峰值，随后随着房间内温度的降低，空调负荷从电网吸收的功率有所减小，降温负荷也随之逐渐下降。

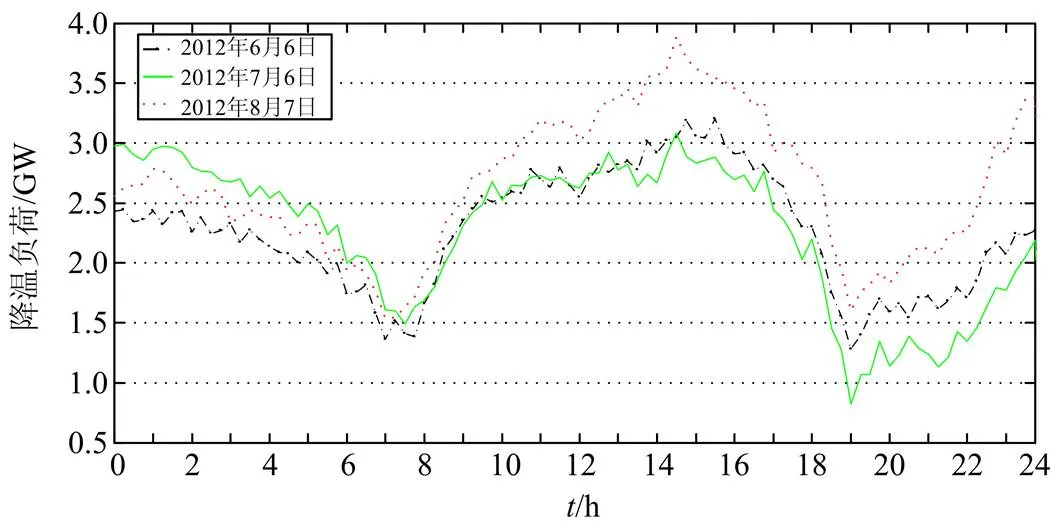
图4 2012年夏季部分工作日的降温负荷曲线

日最大降温负荷可通过求取日降温负荷曲线的最大值得到，统计分析可知，广州市2009~2012年夏季工作日的日最大降温负荷与日最大负荷的比值分布如表1所示，可以看出，二者的比值主要集中在25%~35%，比值位于这个范围内的天数约占夏季工作日总数的56.3%~80.0%，而比值的最大值往往接近40%。广州市2009年~2012年夏季日最大降温负荷的变化如图5所示。

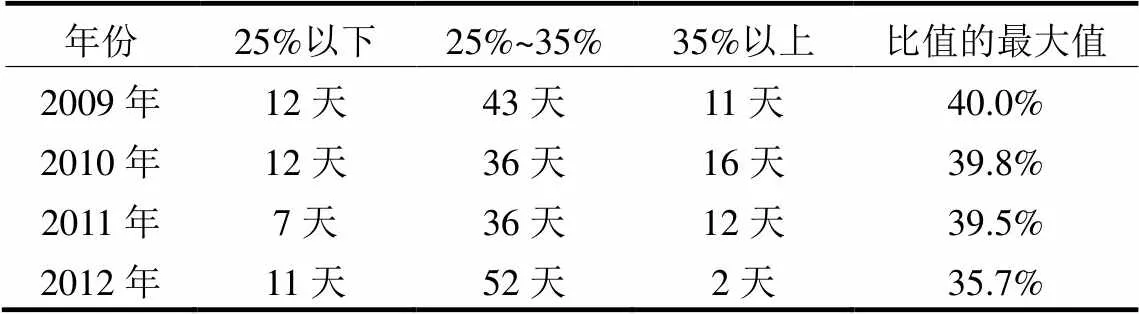
表1 夏季工作日日最大降温负荷与日最大负荷比值的分布

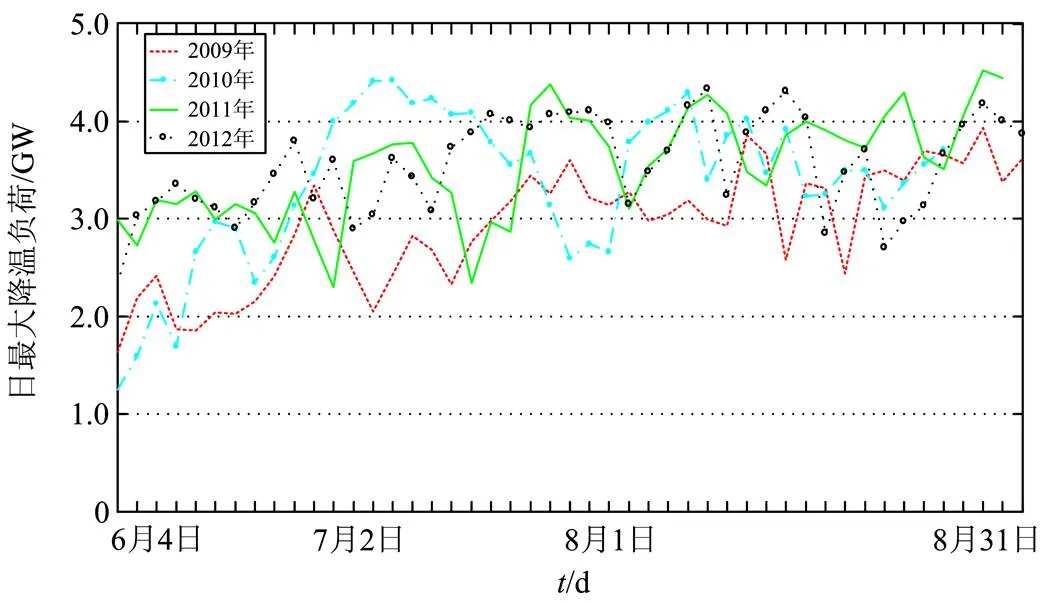
图5 2009~2012年夏季工作日的日最大降温负荷变化

2 降温负荷与温度的相关性分析

相关系数是反映变量间变化关系密切程度的一个统计指标，其绝对值越大，表示相关性越强，二者越接近于线性关系[18]。长度都为的x序列与y序列的相关系数r计算如式(1)所示。

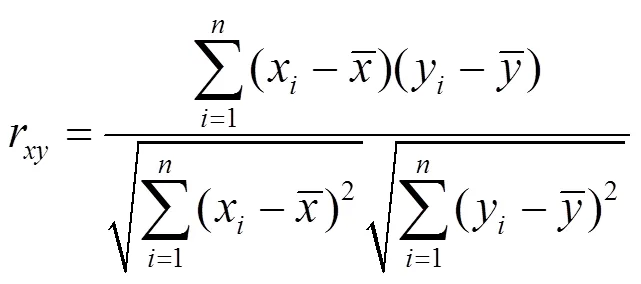
为了避免其他气象因素的影响，选取无降雨(日降雨量小于10 mm)的工作日为研究对象，利用式(1)计算广州市2009~2012年夏季工作日的日最大降温负荷与日最高温度之间的相关系数，如表2所示。可以看出，日最大降温负荷与日最高温度之间的相关系数都大于0.7，相关性强。与最大负荷比较法计算日最大降温负荷相比，本文提出方法计算的日最大降温负荷与日最高温度之间的相关系数更大，日最大降温负荷与日最高温度的变化之间更趋近于线性相关关系。

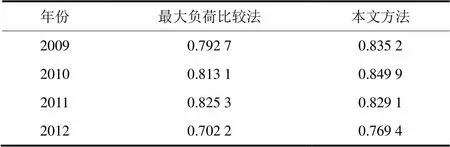
表2 夏季工作日日最大降温负荷与日最高温度的相关系数

3 日最大降温负荷预测模型

3.1 回归模型的建立

回归分析常用来处理不完全确定的变量之间的相关关系，拟合函数可由最小二乘法求得，使各点拟合值与实际值之差的平方和最小，如式(2)，

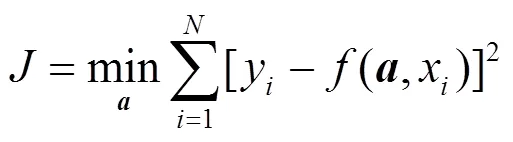
其中：为自变量；为因变量；()为拟合函数；为拟合函数()的待定系数向量。

本文以广州市2009~2011年的历史负荷和气象数据为依据，分别利用一次函数、二次函数和分段函数对日最大降温负荷与日最高温度之间关系进行了函数拟合，结果如下：

1) 一次函数拟合

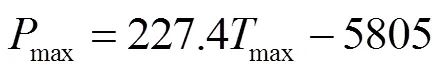
2) 二次函数

3) 分段函数

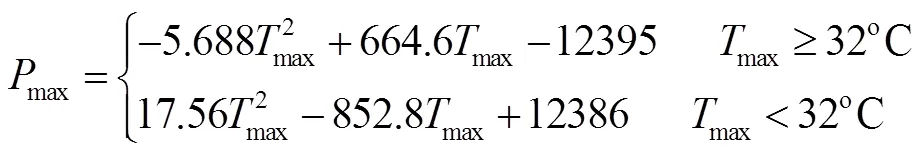
由获得的拟合函数以及日最高温度对2012年夏季工作日的日最大降温负荷进行预测，对于不同拟合函数预测的相对误差如表3所示，不同拟合函数下的预测曲线与实际剥离曲线比较如图6所示。可以看出，三种模型的预测精度相近，预测的相对误差主要分布在-5%~5%，预测精度较高。与一次回归模型和二次回归模型比较，分段回归模型的最大相对误差和平均相对误差都有所减小，且预测曲线趋势更接近于实际剥离的日最大降温负荷曲线，更为准确地反映了日最大降温负荷与日最高温度之间的关系。

表3 不同拟合函数预测的相对误差

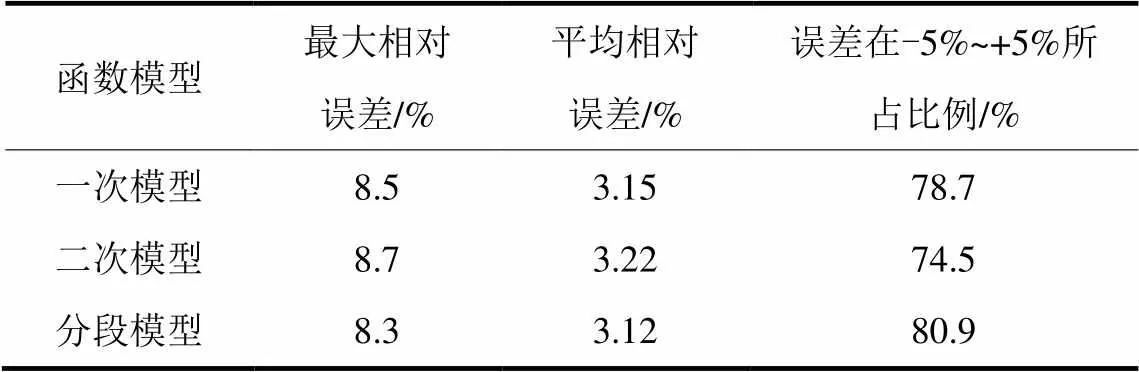
Table 3 Relative error of different prediction model

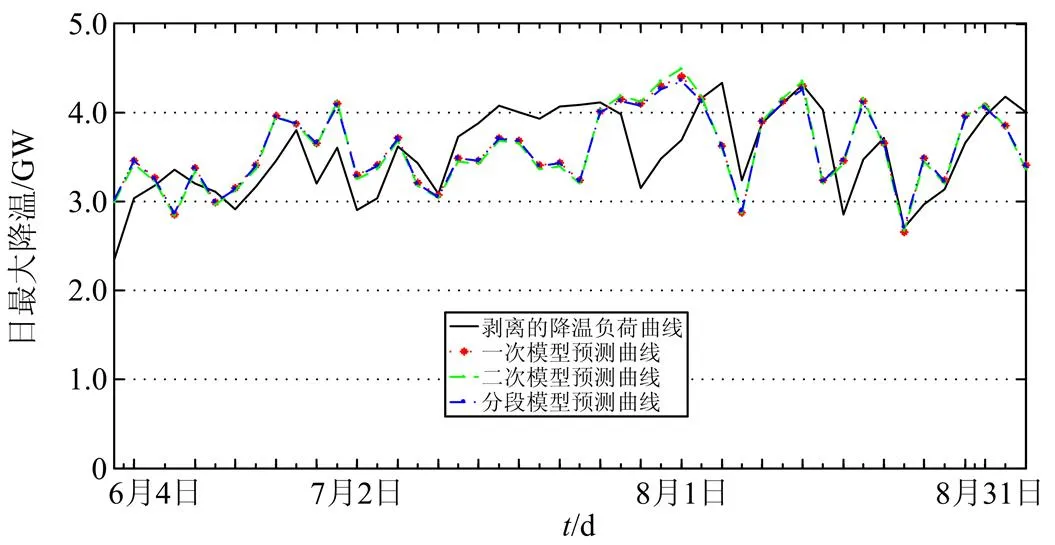
图6 三种模型下的预测曲线比较

3.2 温度累积效应

温度累积效应是指人们的体感温度滞后于外界温度的变化，进而用电行为的变化也会跟着有所滞后[19-20]。当连续几天出现高温天气时，即使接下来的气温下降，电力负荷也不会明显下降；同样，当连续几天温度较低时，即使接下来的气温升高，电力负荷也不会有明显的升高。图7展示了广州市2012年8月份日最大负荷和日最高温度变化的归一化曲线，可以看出，工作日的日最高负荷一般随日最高温度的增减而增减，但8月7日、8日、9日出现连续高温后，当8月10日的日最高温度明显下降时，日最大负荷也不会有明显的下降，这就是明显的温度累积效应现象，连续低温时的温度累积效应与之相似。

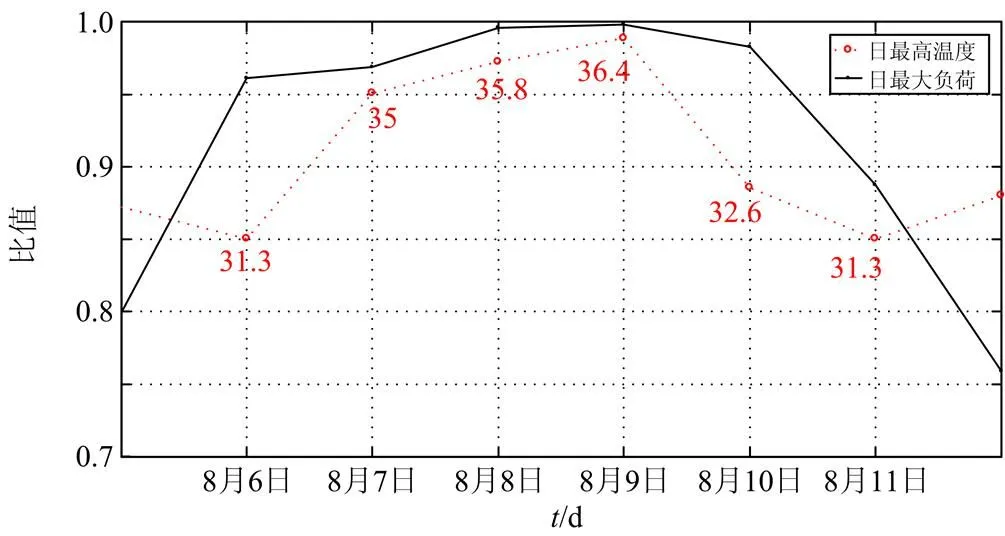
图7 广州市2012年8月份日最大负荷和日最高温度的归一化曲线

由于人们对于空调的使用主要取决于体感温度，故温度累积效应现象会对分析降温负荷与气温之间的内在联系产生影响，为了消除温度累积效应的影响，目前已有一些文献对温度累积效应对负荷变化的影响进行了研究[21-25]，本文通过对外界实际温度进行修正来近似反映人们的体感温度，考虑温度累积效应的温度修正如式(3)所示。

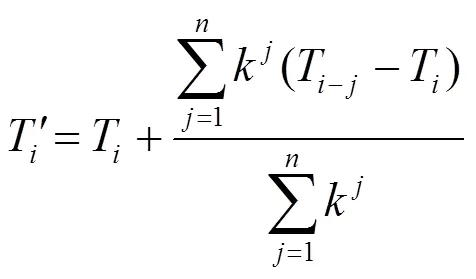
其中：T为待预测日的温度；为待预测日的修正温度；T表示待预测日的天前的温度；为修正系数，取值范围为0<<1，修正系数取值随地区经济状况的不同而不同。可以看到，待预测日的修正温度在其实际温度基础上，叠加上前几天与当天温度差的加权和，以反映前几天气温的累积效应对于当天人们体感温度的影响。当式(3)中的值大于3时，项对值的影响极小，可忽略，于是式(3)可简写为式(4)。

(4)

通过对广州市2009年~2012年的历史负荷和温度数据分析发现：当广州市日最高温度连续3天高于33℃或者连续3天低于28℃时会出现明显的温度累积效应，因此需要对温度累积效应明显的工作日的温度进行修正。利用式(4)对夏季工作日的日最高温度进行修正，取修正系数=0.5，再结合前面获得的分段拟合函数对2012年夏季工作日的日最大降温负荷进行预测，温度修正前后的预测误差对比如表4所示，修正后的预测曲线如图8所示。可以看出，考虑温度累积效应对温度进行修正后，日最大降温负荷预测的平均相对误差和最大相对误差都有了明显的下降，而且预测误差更集中分布在-5%~+5%的误差范围内，预测精度有了明显的提高。

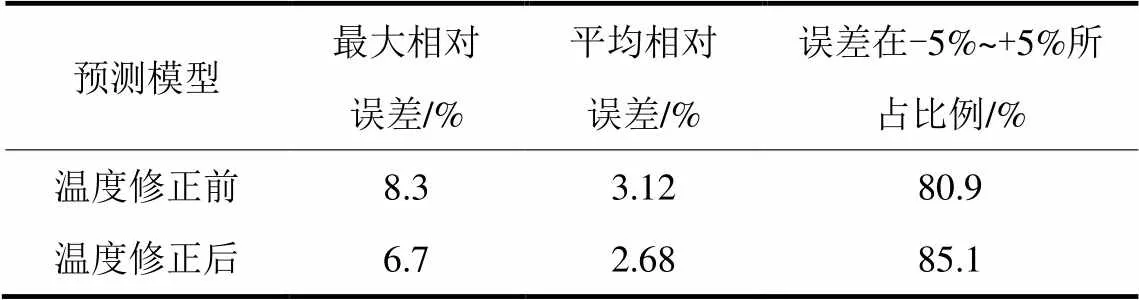
表4 考虑温度累积效应前后的预测误差比较

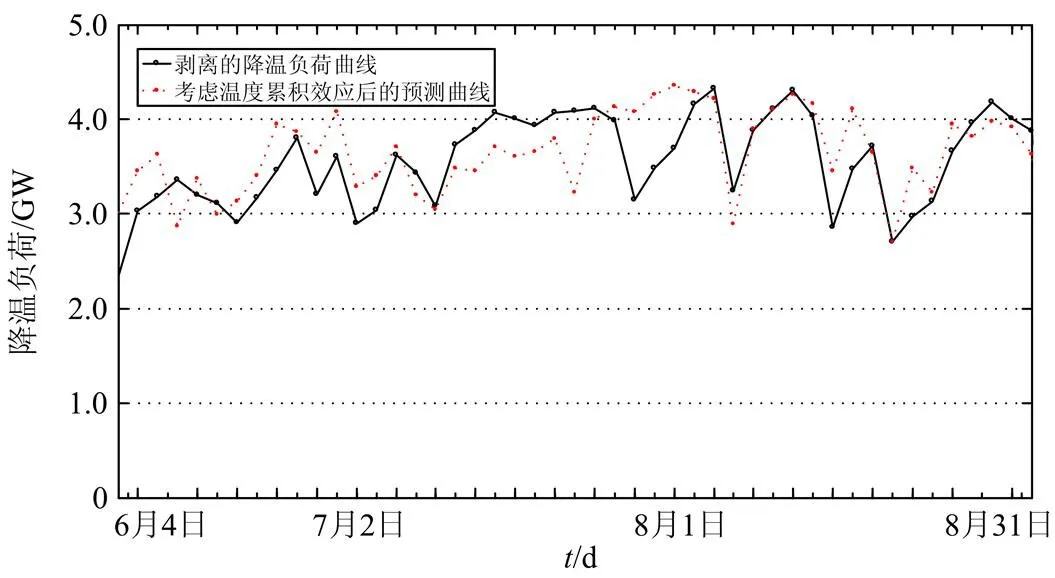
图8 考虑温度累积效应后的预测结果

4 结论

(1) 考虑了基准负荷的逐日增长量，以无降温负荷日的负荷曲线为基础，基于GM(1,1)模型预测出夏季每个工作日的基准负荷曲线，从而更准确地剥离出夏季日降温负荷曲线，并分析广州市夏季工作日降温负荷曲线的“W”型变化特性。

(2) 在相关性分析的基础上，建立了不同的回归模型对日最大降温负荷进行预测，提出了分段回归预测模型，使得日最大降温负荷预测值具有更高的精度。

(3) 提出了近似反映人们体感温度的考虑温度累积效应的修正公式，通过对温度进行修正后，有效地提高了分段回归模型对于日最大降温负荷的预测精度。

[1] 康重庆, 夏清, 张伯明. 电力系统负荷预测研究综述与发展方向的探讨[J]. 电力系统自动化, 2004, 28(17): 1-11.

KANG Chongqing, XIA Qing, ZHANG Boming. Review of power system load forecasting and its development[J]. Automation of Electric Power Systems, 2004, 28(17): 1-11.

[2] 马哲, 舒勤. 基于ESPRIT分解算法的短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(7): 90-96.

MA Zhe, SHU Qin. Short term load forecasting based on ESPRIT integrated algorithm[J]. Power System Protection and Control, 2015, 43(7): 90-96.

[3] 崔和瑞, 彭旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(4): 108-114.

CUI Herui, PENG Xu. Summer short-term load forecasting based on ARIMAX model[J]. Power System Protection and Control, 2015, 43(4): 108-114.

[4] 李龙, 魏靖, 黎灿兵, 等. 基于人工神经网络的负荷模型预测[J]. 电工技术学报, 2015, 30(8): 225-230.

LI Long, WEI Jing, LI Canbing, et al. Prediction of load model based on artificial neural network[J]. Transactions of China Electrotechnical society, 2015, 30(8): 225-230.

[5] 谷云东, 张素杰, 冯君淑. 大用户电力负荷的多模型模糊综合预测[J]. 电工技术学报, 2015, 30(23): 110-115.

GU Yundong, ZHANG Sujie, FENG Junshu. Multi-model fuzzy synthesis forecasting of electric power loads for larger consumers[J]. Transactions of China Electrotechnical society, 2015, 30(23): 110-115.

[6] 王玉龙, 崔玉, 李鹏, 等. 基于小波分析改进的神经网络模型电力系统负荷预测[J]. 电网与清洁能源, 2015, 31(2): 16-20.

WANG Yulong, CUI Yu, LI Peng, et al. Load forecasting of power system based on wavelet analysis improved neural network Model[J]. Power System and Clean Energy, 2015, 31(2): 16-20.

[7] 王宁, 谢敏, 邓佳梁, 等. 基于支持向量机回归组合模型的中长期降温负荷预测[J]. 电力系统保护与控制, 2016, 44(3): 92-97.

WANG Ning, XIE Min, DENG Jialiang, et al. Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression[J]. Power System Protection and Control, 2016, 44(3): 92-97.

[8] 康重庆, 周安石, 王鹏, 等. 短期负荷预测中实时气象因素的影响分析及其处理策略[J]. 电网技术, 2006, 30(7): 5-10.

KANG Chongqing, ZHOU Anshi, WANG Peng, et al. Impact analysis of hourly weather factors in short-term load forecasting and its processing strategy[J]. Power System Technology, 2006, 30(7): 5-10.

[9] LU N, TAYLOR T, JIANG W, et al. Climate change impacts on residential and commercial loads in the Western U.S. Grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 480-488.

[10] 石峰, 吴笛, 李宝珠. 重庆市夏季空调负荷分析及有效调节空调负荷的措施建议[J]. 电力技术经济, 2008, 20(1): 42-46.

SHI Feng, WU Di, LI Baozhu. Analysis of air-conditioning load in summer and suggestion for effective measures of air-conditioning load in Chongqing[J]. Electric Power Technology Economics, 2008, 20(1): 42-46.

[11] 童述林, 文福拴. 节能减排环境下广东省年最大降温负荷的测算与分析[J]. 华北电力大学学报(自然科学版), 2010, 37(5): 32-37.

TONG Shulin, WEN Fushuan. Calculation and analysis of the annual maximum high-temperature related load in the energy saving and emission reduction environment in Guangdong Province[J]. Journal of North Electric Power University (Natural Science), 2010, 37(5): 32-37.

[12] 刘旭, 罗滇生, 姚建刚, 等. 基于负荷分解和实时气象因素的短期负荷预测[J]. 电网技术, 2009, 33(12): 94-100.

LIU Xu, LUO Diansheng, YAO Jiangang, et al. Short- term load forecasting based on load decomposition and hourly weather factors[J]. Power System Technology, 2009, 33(12): 94-100.

[13] 廖峰, 徐聪颖, 姚建刚, 等. 常德地区负荷特性及其影响因素分析[J]. 电网技术, 2012, 36(7): 117-125.

LIAO Feng, XU Congying, YAO Jiangang, et al. Load characteristics of changed region and analysis on its influencing factors[J]. Power System Technology, 2012, 36(7): 117-125.

[14] 刘继东, 韩学山, 楚成博, 等. 考虑非气象因素的电网夏季降温负荷研究[J]. 电力自动化设备, 2013, 33(2): 40-46.

LIU Jidong, HAN Xueshan, CHU Chengbo, et al. Cooling load of summer grid considering non-meteorological factors[J]. Electric Power Automation Equipment, 2013, 33(2): 40-46.

[15] 焦润海, 苏辰隽, 林碧英, 等. 基于气象信息因素修正的灰色短期负荷预测模型[J]. 电网技术, 2013, 37(3): 720-725.

JIAO Runhai, SU Chenjun, LIN Biying, et al. Short-term load forecasting by grey model with weather factor-based correction[J]. Power System Technology, 2013, 37(3): 720-725.

[16] 李晓梅, 周晖, 李冬梅. 夏季日峰荷与有效温度的灰色建模及灵敏度分析[J]. 电网技术, 2004, 28(14): 23-27.

LI Xiaomei, ZHOU Hui, LI Dongmei. Grey model and sensitivity analysis of summer daily peak load and effective temperature[J]. Power System Technology, 2004, 28(14): 23-27.

[17] 邓聚龙. 灰色预测与决策[M]. 武汉: 华中理工大学出版社, 1986: 97-148.

[18] 贺辉. 电力负荷预测和负荷管理[M]. 北京: 中国电力出版社, 2013: 213-226.

[19] 李嘉龙, 李小燕, 刘思捷, 等. 考虑气温累积效应的短期负荷预测[J]. 华北电力大学学报(自然科学版), 2013, 40(1): 49-54.

LI Jialong, LI Xiaoyan, LIU Sijie, et al. Short-term load forecasting considering the accumulative effects of temperatures[J]. Journal of North China Electric Power University(Natural Science), 2013, 40(1): 49-54.

[20] 张凯, 姚建刚, 李伟, 等. 负荷预测中的温度热累积效应分析模型及处理方法[J]. 电网技术, 2008, 32(4): 67-71.

ZHANG Kai, YAO Jiangang, LI Wei, et al. Analysis model and processing approach for thermal cumulative effect of temperature in load forecasting[J]. Power System Technology, 2008, 32(4): 67-71.

[21] 陈根永, 史敬天, 毛晓波, 等. 考虑温度积累效应的短期电力负荷预测方法研究[J]. 电力系统保护与控制, 2010, 38(22): 100-104.

CHEN Genyong, SHI Jingtian, MAO Xiaobo, et al. Study on the method of short-term load forecasting considering the accumulation effect of temperature[J]. Power System Protection and Control, 2010, 38(22): 100-104.

[22] 金丽莉, 谭风雷, 吴志坚, 等. 考虑积温效应的负荷预测研究[J]. 电力需求侧管理, 2013, 15(1): 7-10.

JIN Lili, TAN Fenglei, WU Zhijian, et al. The study of load forecasting accounting accumulated temperature effect[J]. Power Demand Side Management, 2013, 15(1): 7-10.

[23] 张庆华, 王云洁, 卢毅. 考虑积温效应的夏季日最大负荷预测研究[J]. 电力需求侧管理, 2013, 15(6): 1-5.

ZHANG Qinghua, WANG Yunjie, LU Yi. Study on summer daily peak load forecasting considering the accumulation effect of temperature[J]. Power Demand Side Management, 2013, 15(6): 1-5.

[24] 高赐威, 李倩玉, 苏卫华, 等. 短期负荷预测中考虑积温效应的温度修正模型研究[J]. 电工技术学报, 2015, 30(1): 242-249.

GAO Ciwei, LI Qianyu, SU Weihua, et al. Temperature correction model research considering temperature cumulative effect in short-term load forecasting[J]. Transactions of China Electrotechnical society, 2015, 30(4): 242-249.

[25] 黎灿兵, 杨朋, 刘玮, 等. 短期负荷预测中考虑夏季气温累积效应的方法[J]. 电力系统自动化, 2009, 33(9): 96-99.

LI Canbing, YANG Peng, LIU Wei, et al. An analysis of accumulative effect of temperature in short-term load forecasting[J]. Automation of Electric Power Systems, 2009, 33(9): 96-99.

(编辑 葛艳娜)

An estimating and forecasting method for daily maximum cooling load in summer

LIU Sijie1, ZHANG Haipeng2, LIN Shunjiang2, LIU Mingbo2, LI Jialong1, WANG Yi1, SUN Qian1

(1. Dispatch and Control Center of Guangdong Power Grid, Guangzhou 510600, China; 2. School of Electric Power Engineering, South China University of Technology, Guangzhou 510640, China)

With the widely use of cooling equipment such as air conditioner, the influence of cooling-load on security and economy operation of power system is increasingly obvious. According to the historical load data and temperature data, this paper analyses the correlation between cooling-load and temperature in summer in Guangzhou city. First, considering the daily increment of base load in summer, daily base load curve of power grid in summer is predicted by using GM(1,1) model, and then the cooling-load curve in summer is separated accurately, and the ‘W’ changing feature of daily cooling-load curve is also analyzed. Second, based on the correlation analysis between daily maximum cooling-load and daily maximum temperature, this paper establishes piecewise regression model between them, and predicts the daily maximum cooling-load. Finally, considering the influence of accumulative effect of temperature, this paper improves the piecewise regression model to further increase the prediction accuracy, which can provide basis to accurately predict the daily peak load in summer of power grid. This work is supported by National Natural Science Foundation of China (No. 51207056).

cooling-load; GM(1,1) model; correlation analysis; piecewise regression model; accumulative effect of temperature

10.7667/PSPC150822

国家自然科学基金项目(51207056)；广东电网公司电力调度控制中心科技项目(GDDW2020130303SC00044)

2015-08-15；

2016-02-21

刘思捷(1985-)，女，工学学士，助理工程师，研究方向为电力系统调度运行；张海鹏(1991-)，男，硕士研究生，主要研究方向为电力系统优化与控制；林舜江(1980-)，男，通信作者，博士，副研究员，硕士生导师，主要研究方向为电力系统优化与控制。E-mail: linshj@scut.edu.cn