轨道振动特性对高速铁路钢轨波磨的影响

谷永磊，赵国堂，王衡禹，温泽峰，金学松

(1.北京交通大学 土木建筑工程学院，北京　100044；2.中国铁道科学研究院 铁道建筑研究所，北京　100081；3.中国铁路总公司，北京　100844；4.西南交通大学 牵引动力国家重点实验室，四川 成都　610031)

钢轨波磨几乎出现在所有类型的轨道结构上，不仅导致车辆和轨道结构激烈的振动，产生噪声，影响旅客乘坐舒适度，大大增加养护部门的维修工作量和维修费用，而且给行车安全带来了隐患[1-5]。

高速铁路上的钢轨波磨在日本新干线小半径曲线上发生过[1]，我国京津城际铁路一条半径300 m的曲线上也发生过钢轨波磨。我国某高速铁路无砟轨道直线段钢轨出现波磨后，相关部门开展了大量的研究工作[6]，本文通过现场测试和仿真分析，研究轨道结构的振动特性与高速铁路钢轨波磨的内在关系以及轨道振动特性对钢轨波磨影响的机理。

1　高速铁路无砟轨道钢轨波磨特征

图1为我国某高速铁路无砟轨道线路出现的典型钢轨波磨。图2和图3分别给出了采用钢轨波磨测量小车(CAT)测得的不同区段典型钢轨波磨的频谱特性[7]。

区段A距离起点站较近，列车通过该区段时的速度一般在270 km·h-1左右。由图2可以看出，钢轨波磨的显著波长为50～65 mm，次显著波长为100～125 mm，另外还有30，500和800 mm波长的波磨存在。

图1　某高速铁路钢轨波磨特征

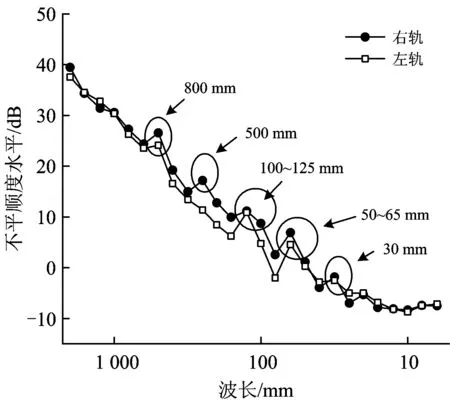
图2　某高速铁路区段A的钢轨波磨频谱特性

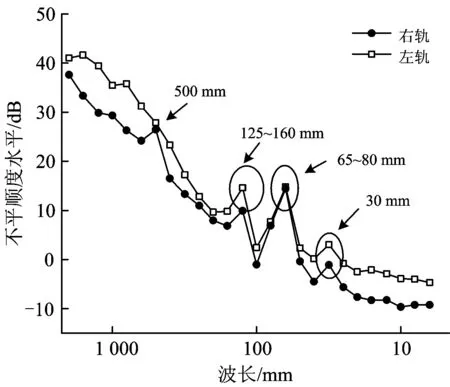
图3　某高速铁路区段B的钢轨波磨频谱特性

区段B的列车通过速度达到300 km·h-1。由图3可以看出，钢轨波磨的显著波长为65～80 mm，次显著波长为125～160 mm。另外在钢轨上也能发现波长为30 mm的波磨，右轨还存在500 mm波长的波磨。

2　高速铁路波磨地段轨道振动特性测试分析

为分析钢轨在典型激励下的敏感共振频率，采用图4所示的力锤敲击测试方法，对2个波磨区段的轨道振动特性进行测试。

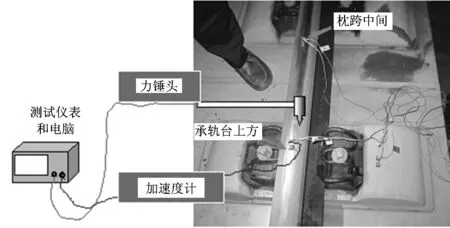
图4　轨道振动特性敲击测试示意图

图5和图6分别给出了在区段A的承轨台上方和枕跨中间进行垂向激励时钢轨的垂向加速度响应。由图5可以看出，当在承轨台上方激励时，承轨台上方的钢轨相对较敏感频率为130～150，810和1 150～1 270 Hz。由图6可以看出，当在枕跨中间激励时，枕跨中间位置的钢轨相对较敏感频率为130～150，920和1 000～1 050 Hz。

当列车以运行速度v(km·h-1)通过波长为λ(m)的钢轨波磨时，对应的通过频率f(Hz)为区段A处于列车加速阶段，列车的平均速度一般为270 km·h-1，波长50～65 mm波磨对应的通过频率为1 150～1 500 Hz，与在承轨台上方或枕跨中间激励时轨道垂向表现出的敏感共振频率1 000～1 270 Hz相近；波长100～125 mm波磨对应的通过频率为600～750 Hz，与轨道垂向表现出的敏感共振频率810和920 Hz比较接近。

(1)

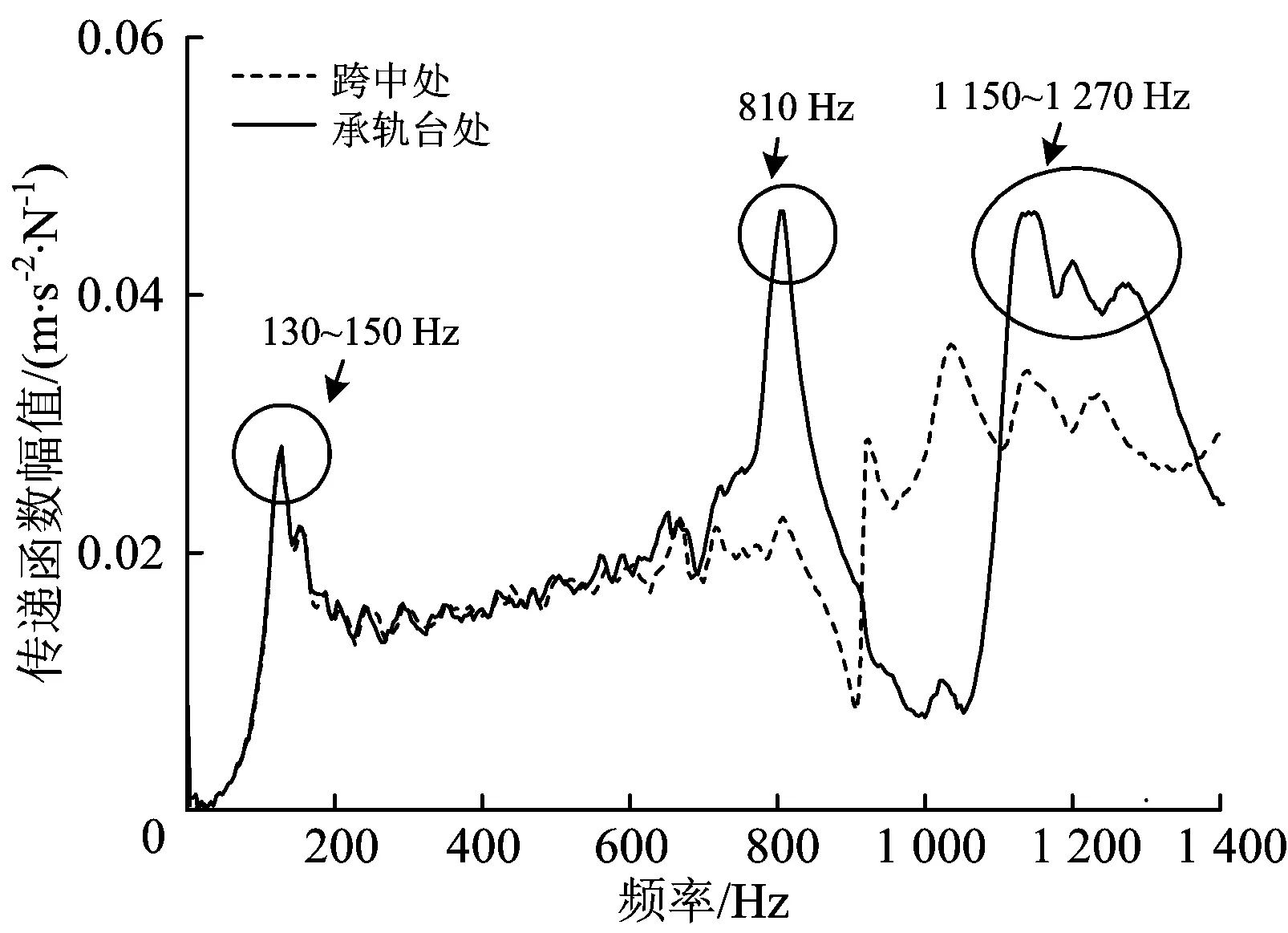
图5　承轨台上方垂向激励下钢轨垂向加速度响应

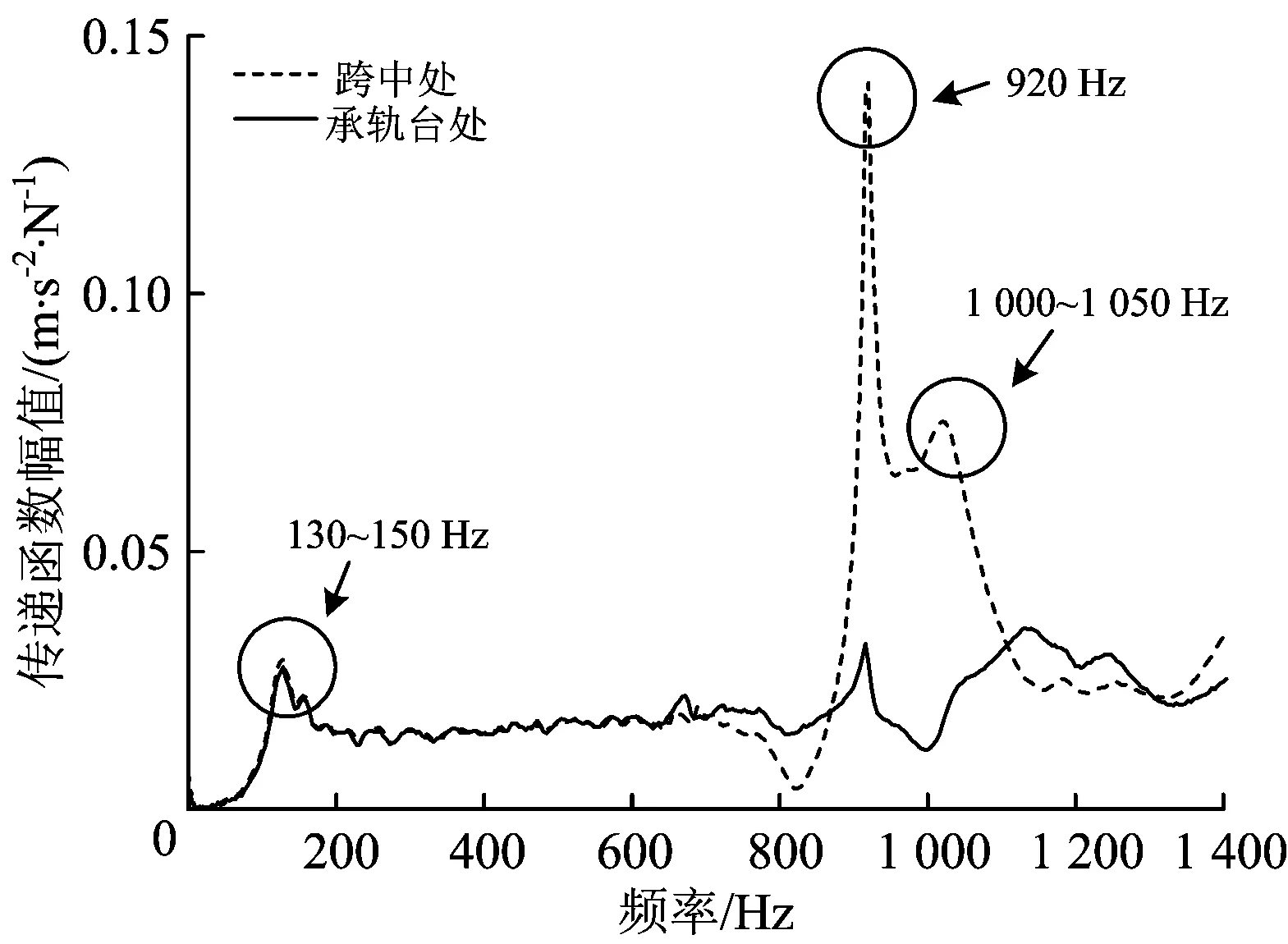
图6　枕跨中间垂向激励下钢轨垂向加速度响应

图7—图9分别给出了在区段B承轨台上方和枕跨中间进行垂向激励时钢轨的垂向和横向加速度响应。由图7—图9可以看出，该轨道结构的垂向共振频率包括130～150，750，810 ，920 和1 050～1 110 Hz，横向共振频率包括70， 630～650，760，920和1 100 Hz。

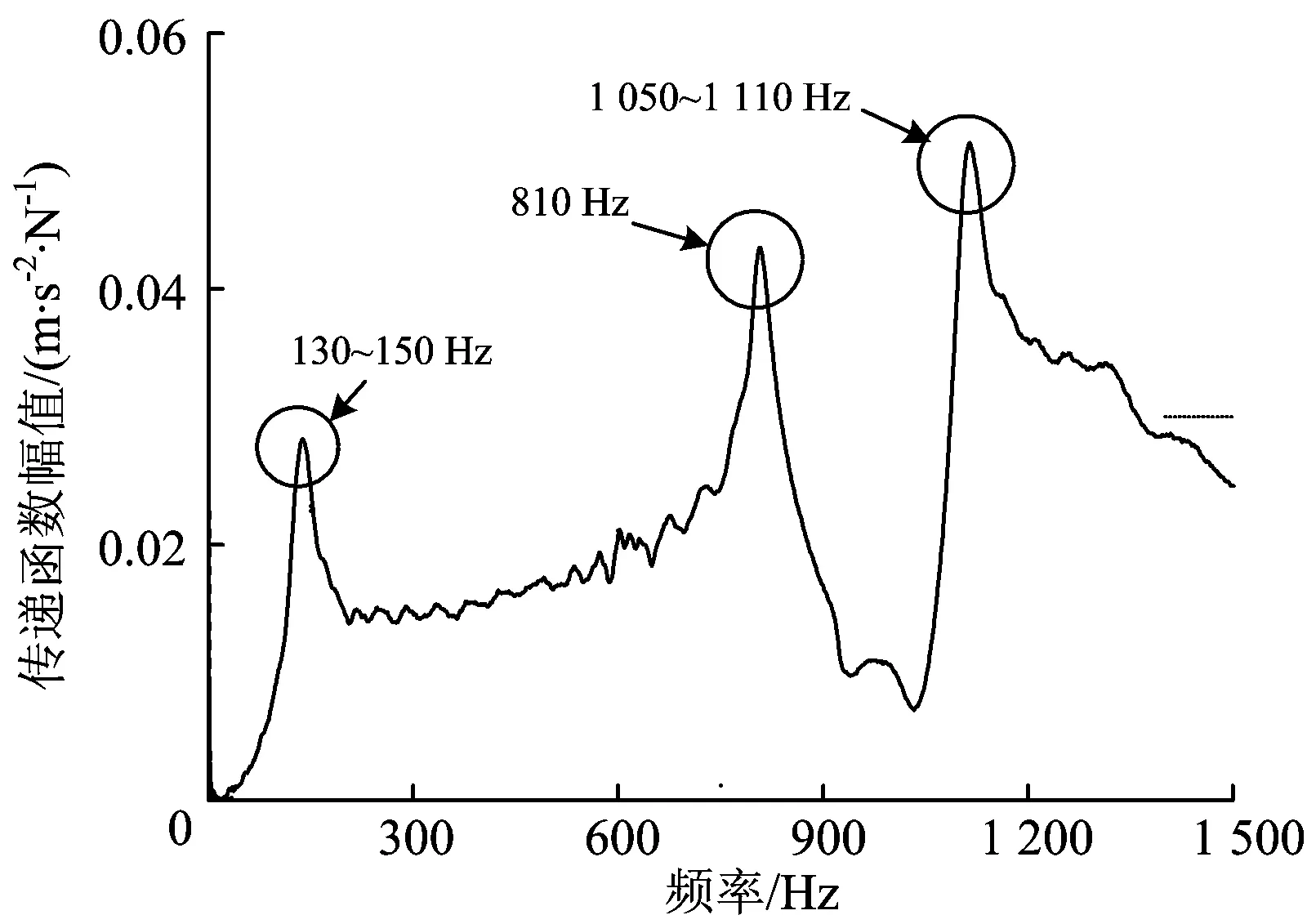
图7　承轨台上方垂向激励下钢轨垂向加速度响应

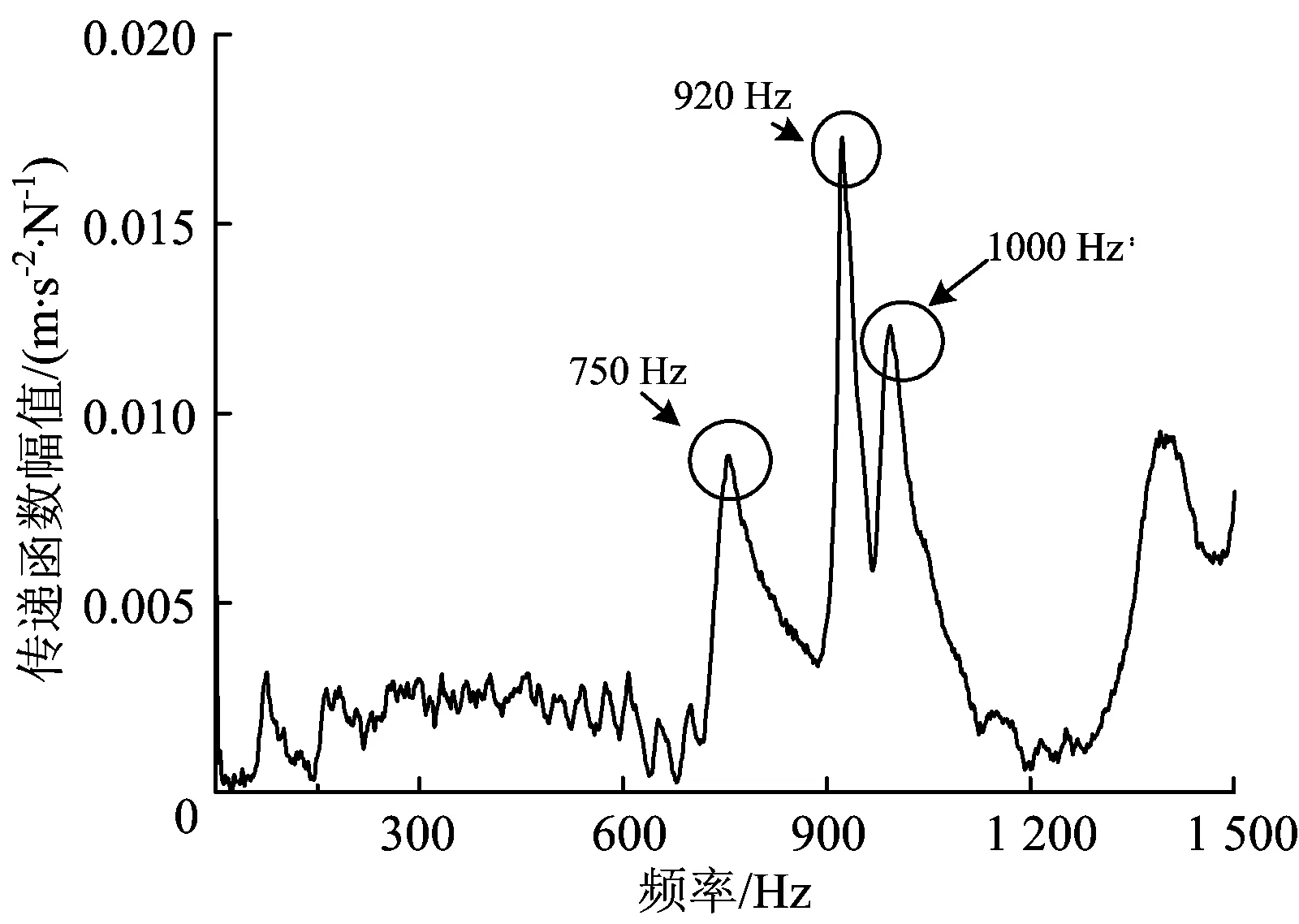
图8　枕跨中间垂向激励下钢轨垂向加速度响应

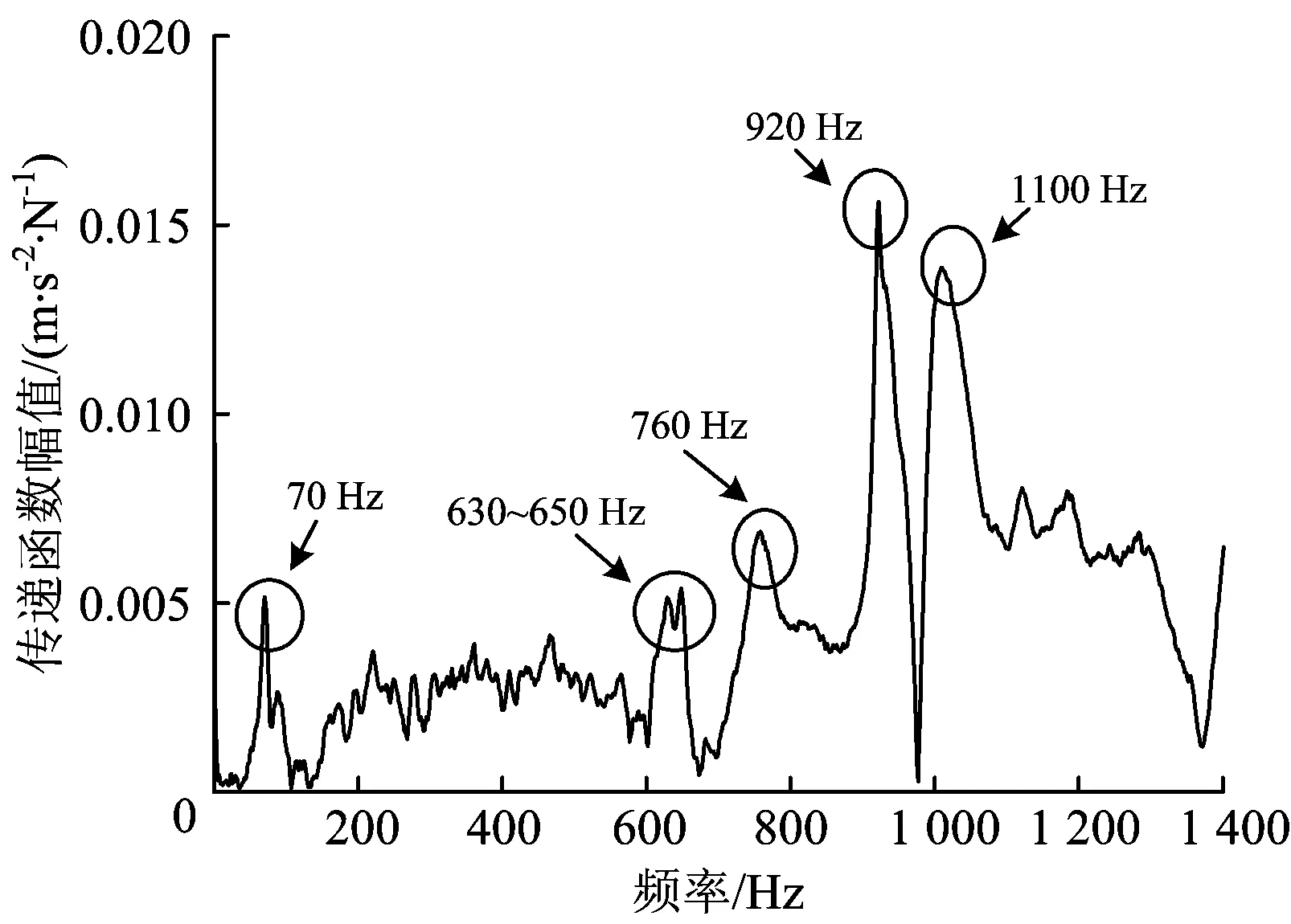
图9　承轨台上方横向激励下钢轨横向加速度响应

由式(1)得到列车以300 km·h-1速度通过显著波长65～80 mm波磨时对应的通过频率为1 041～1 282 Hz，轨道共振的最敏感频率范围920～1 110 Hz与之相近；次显著波长125～160 mm波磨对应的通过频率为521～667 Hz，轨道共振最敏感频率630～810 Hz与之相近。

轨道力锤敲击测试是在无车辆通过时进行的，当车辆通过轨道时由于簧下质量的存在，会导致系统的质量变大，从而使轨道系统的共振频率略有降低。这是某些波磨的通过频率比测试得到的轨道共振敏感频率略低的原因。

由2个区段轨道振动特性的测试结果及考虑车辆簧下质量的影响可知，钢轨波磨与轨道振动特性具有很强的关联性。

3　高速铁路轨道振动特性的仿真分析

为进一步分析波磨产生的原因，建立有限元仿真模型，以区段B为对象进行计算分析。

3.1　仿真计算模型

轨道系统为一个无限长结构，当轨道结构上有一作用力时，该作用力的影响只限于力作用附近的局部区域上。故为提高计算效率，一般选取3块轨道板建立模型进行计算就能够满足分析精度的需要。

应用有限元软件ABAQUS建立CRTSⅡ型板式无砟轨道的计算模型[8]。钢轨和轨道板采用三维实体单元模拟，扣件系统、CA砂浆层均采用弹簧和阻尼单元模拟，如图10所示。计算参数采用所研究的CRTSⅡ型板式无砟轨道的实际参数，钢轨、轨道板和CA砂浆的参数见表1；扣件的垂向刚度为22 MN·m-1，垂向、横向和纵向阻尼分别为200,100和100 kN·s·m-1，间距为0.65 m。考虑轨道结构的对称性，选取轨道结构的一半进行计算分析。

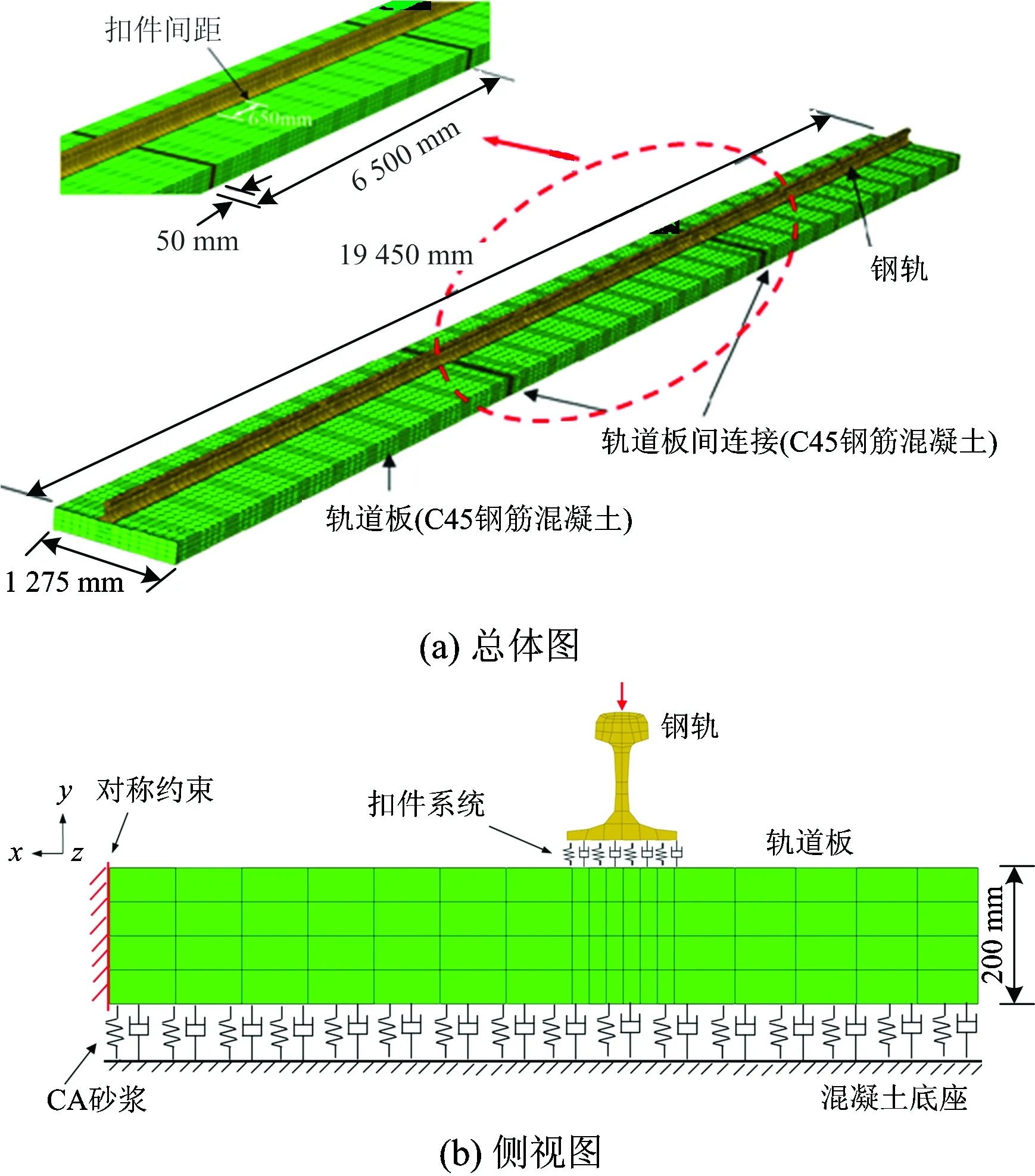
图10　高速铁路无砟轨道结构的有限元模型

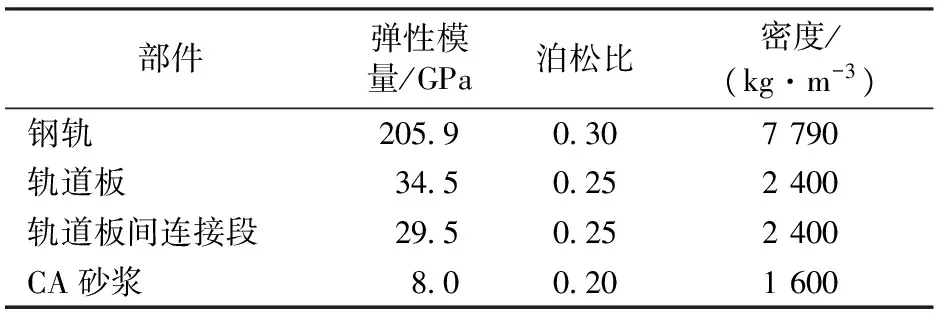
部件弹性模量/GPa泊松比密度/(kg·m-3)钢轨20590307790轨道板3450252400轨道板间连接段2950252400CA砂浆800201600

3.2　模态响应分析

钢轨Pinned-Pinned共振是指钢轨被轨枕以周期性的方式固定下的模态振动。计算得到的轨道结构中钢轨垂向Pinned-Pinned 共振模态如图11所示，共振频率为1 030 Hz。钢轨共振模态的1个波长恰好等于枕跨距离的2倍，且钢轨在枕跨中间的振动幅值最大，而在承轨台上方的振动很小。

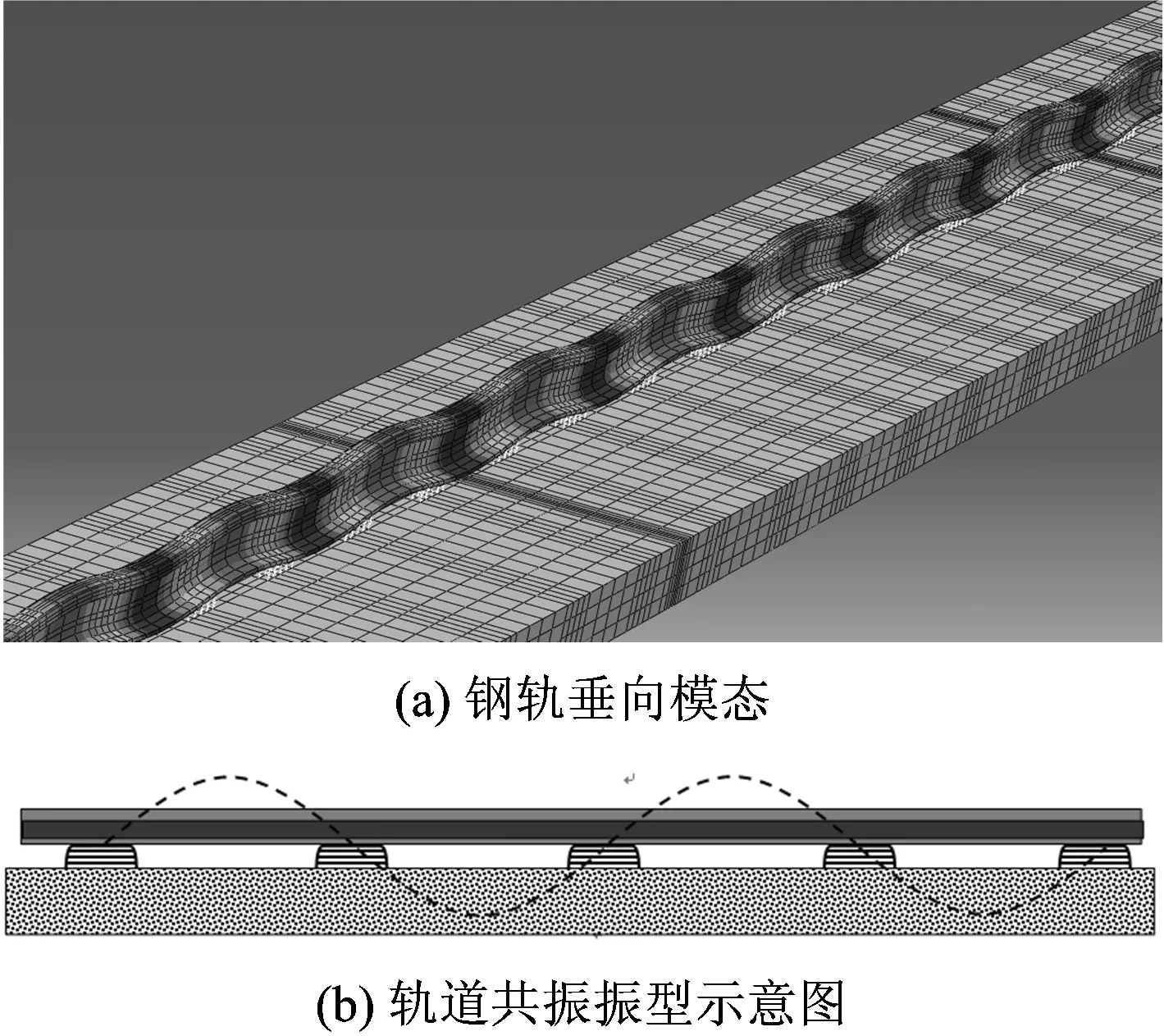
图11　钢轨垂向Pinned-Pinned共振

图12为轨道横向 Pinned-pinned共振模态，共振频率为580 Hz，振型特征与垂向相近，钢轨振动波长也为枕跨长度的2倍，且承轨台上的钢轨振动微小。

图12　钢轨横向Pinned-pinned共振模态

仿真计算分析还发现，轨道结构在520～1 000 Hz共振频率范围内的垂向振动形式是钢轨相对轨道板的弯曲振动，其钢轨振动波长大约为枕跨长度的3倍左右。而在520 Hz以下轨道结构才会出现钢轨和轨道板一起的相对混凝土底座的垂向振动。

3.3　频率响应分析

图13为钢轨垂向位移导纳计算结果。由图13可以看出，在1 400 Hz以下，垂向共振的频率较多，且当频率在1 030 Hz左右时钢轨响应最为明显，该频率为图11所示的钢轨垂向pinned-pinned 共振频率，且该频率位于现场测试所得轨道振动敏感频率带920～1 110 Hz范围内，表明显著波长65～80 mm的波磨与钢轨垂向pinned-pinned共振有关。

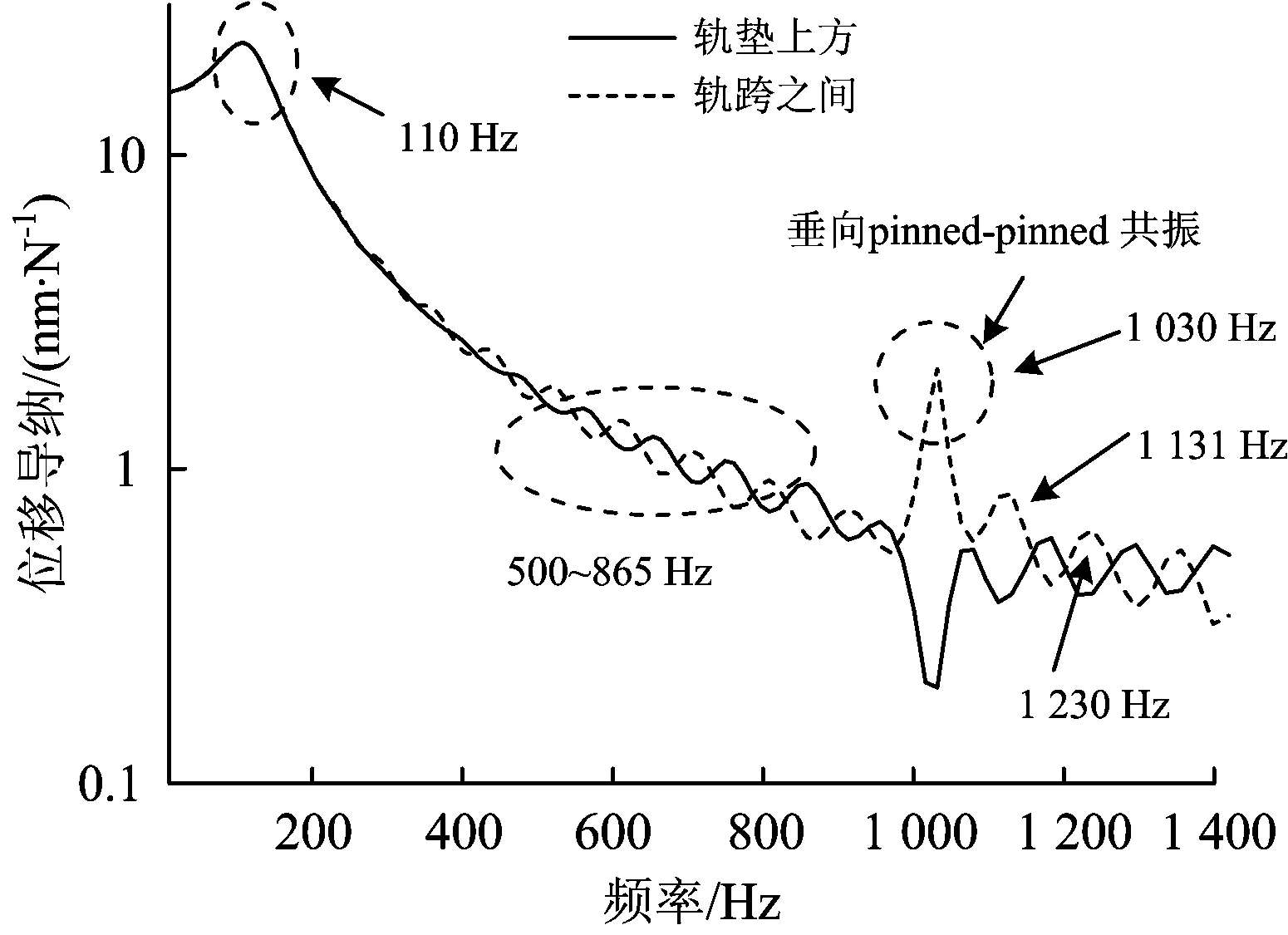
图13　轨道结构钢轨垂向位移导纳计算结果

3.4　宽频激励响应分析

为进一步研究轨道不平顺激励下轨道结构在频率2 000 Hz以下的响应情况，通过建立的轨道模型计算分析了随机力(白噪声)激励的动力响应。

图14为输入的宽频随机激励力的时间历程。图15为枕跨中间钢轨在激励力作用下的加速度频域响应，是经过傅里叶变换后的频率与幅值特性曲线。由图15可以看出，该轨道结构钢轨垂向振动在频率960～1 050 Hz范围内最为活跃，与现场测试结果吻合，进一步说明该轨道结构显著波长65～80 mm的形成与高频的钢轨垂向弯曲振动相关，特别是与钢轨的垂向Pined-pined共振相关联。而在590，660～810和1 150～1 200 Hz等频带，其垂向振动也比较敏感，其振动形式主要为钢轨相对轨道板的振动，但其响应比Pined-pined共振弱。

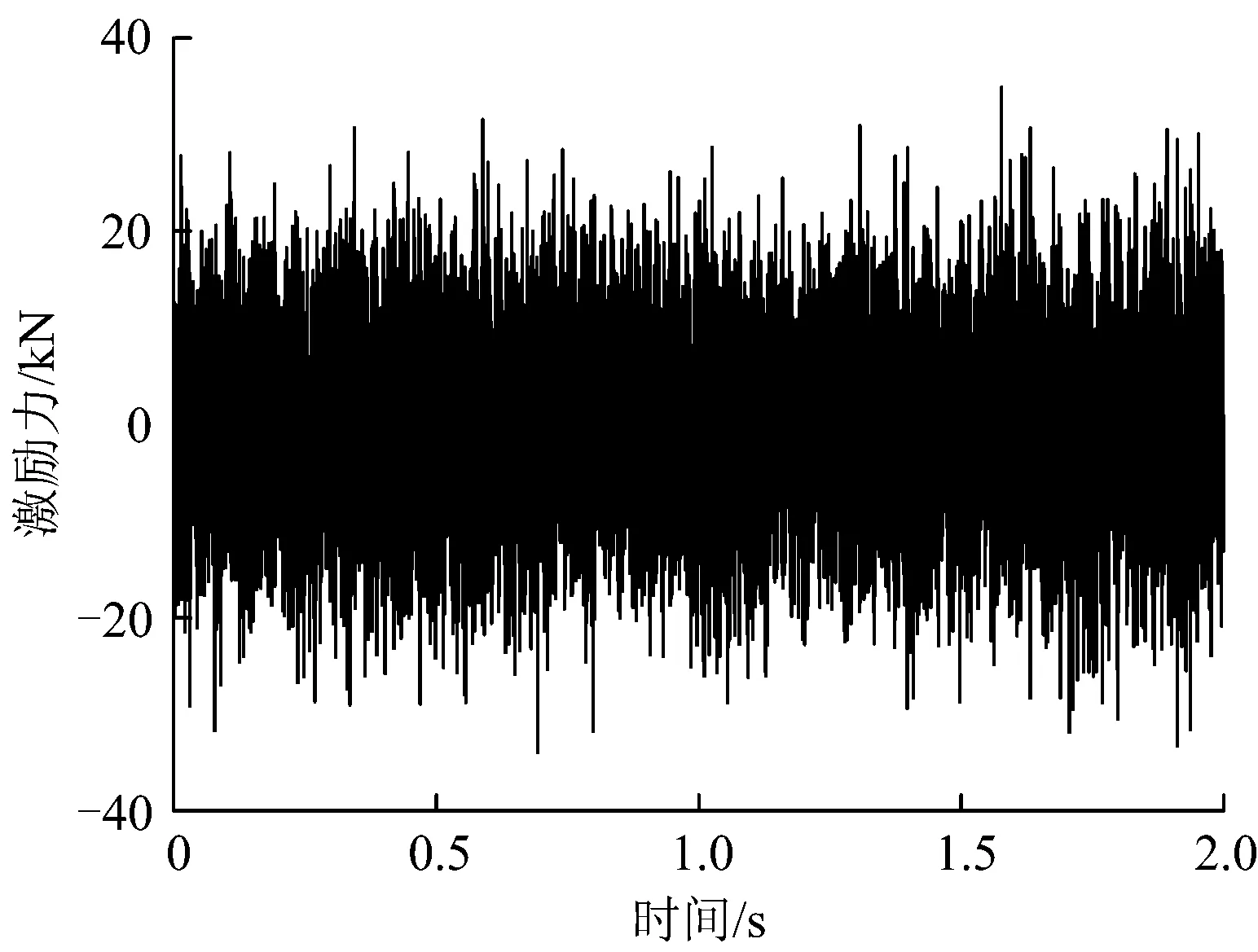
图14　包含1～2 000 Hz随机不平顺的时间历程

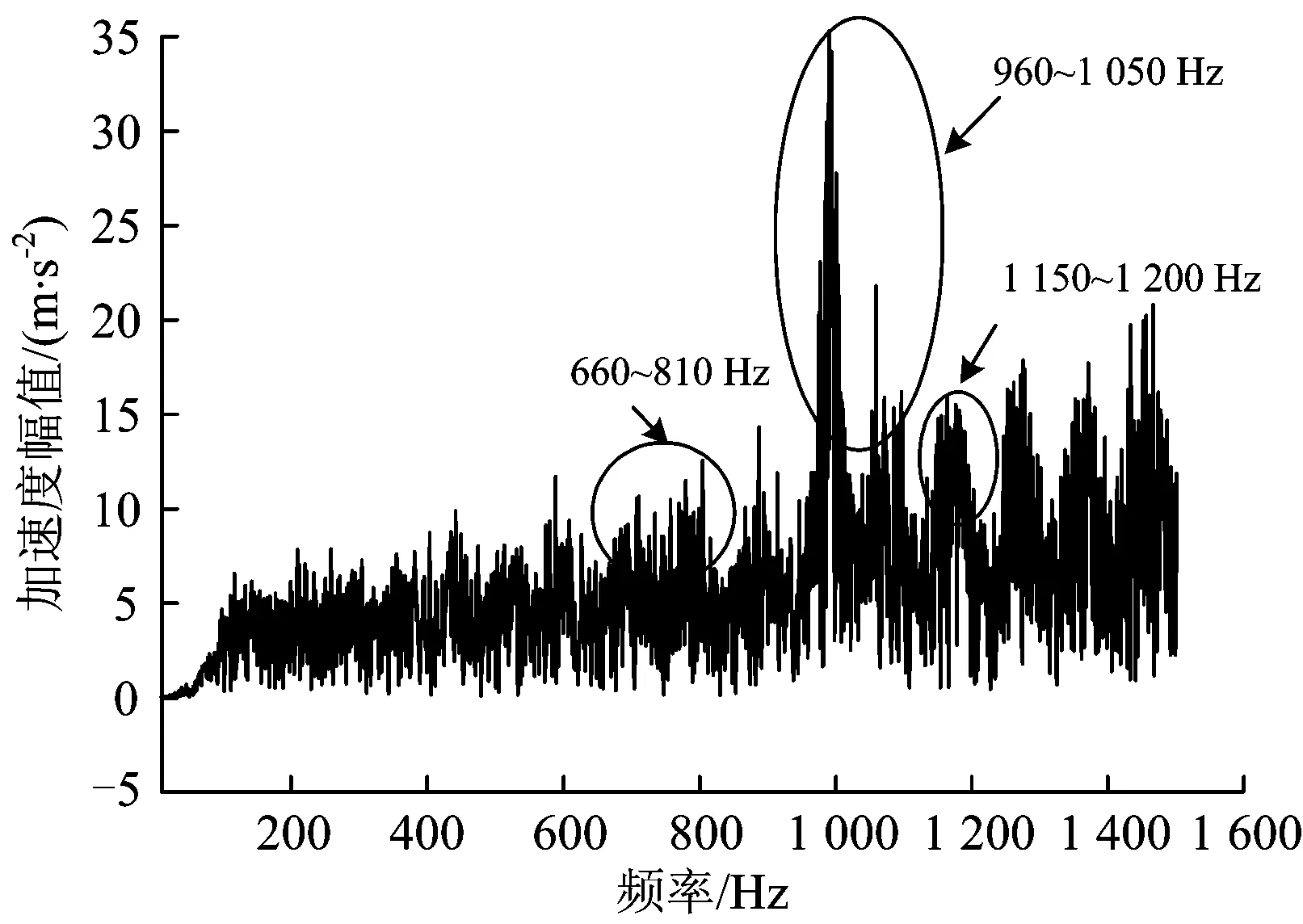
图15　跨中激励时钢轨加速度曲线

图16为轨道承轨台上方钢轨在激励力作用下的加速度频域响应。由图16可见，承轨台上方钢轨在1 000 Hz左右激励力作用时的加速度响应幅值很小，这是由于其为Pinned-pinned共振频率，钢轨扣件将钢轨固定住使其不能相对轨道板振动；而在540～670和720～900 Hz的频率时钢轨振动明显，其为钢轨相对轨道板的振动。所以，波长为125～160 mm的波磨通过频率与钢轨相对轨道板垂向振动的轨道共振频率相似，其产生与钢轨相对轨道板垂向振动相关。

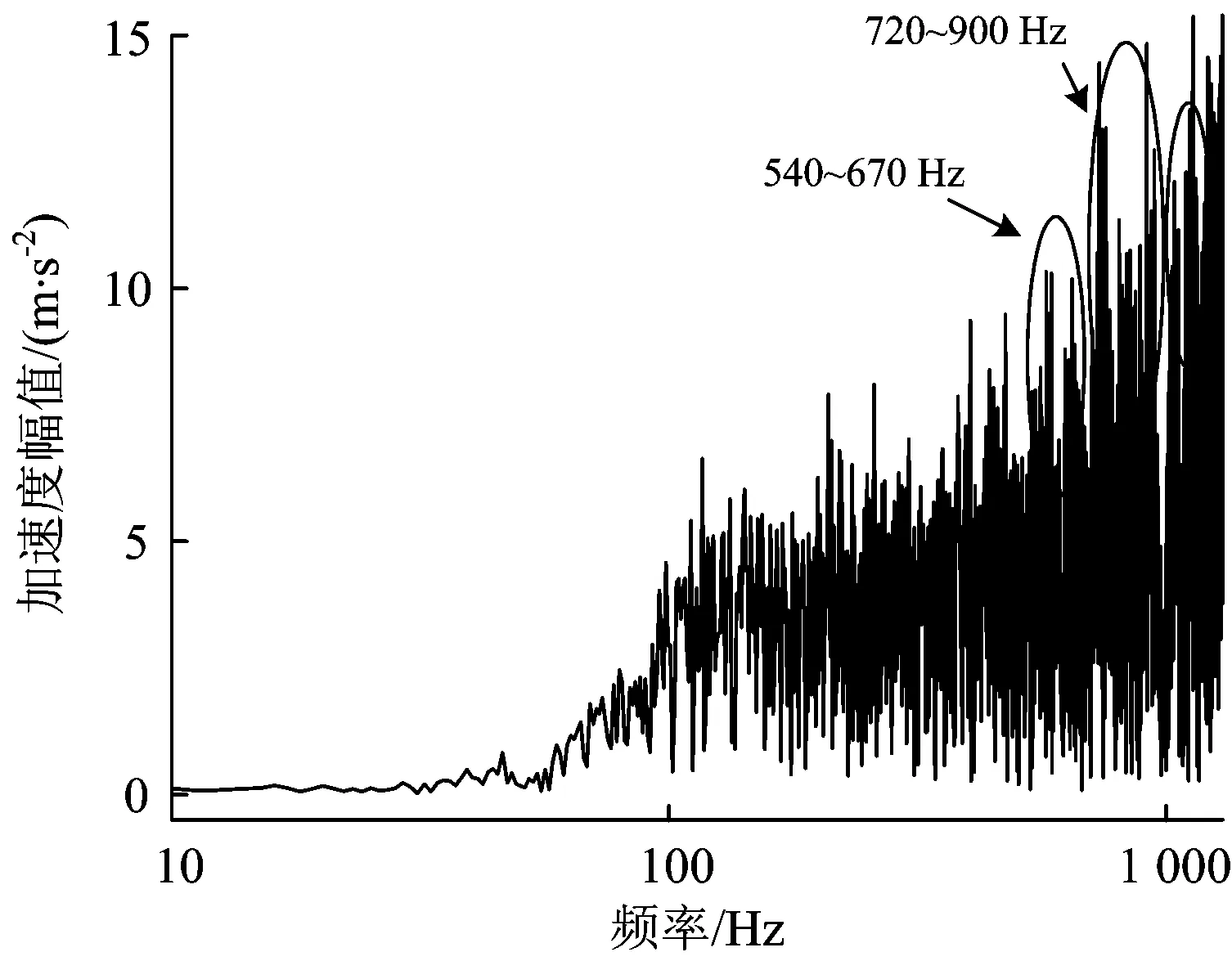
图16　承轨台上方激励时钢轨的加速度曲线

4　结　论

(1)本文研究的我国某高速铁路2段无砟轨道线路上的钢轨波磨均出现2个显著波长，其中区段A为50～65和100～125 mm，区段B为65～80和125～160 mm。对应的通过频率，区段A为1 150～1 500和600～750 Hz，区段B为1 041～1 282和521～667 Hz。

(2)采用力锤敲击法测试波磨地段轨道结构振动特性的结果表明钢轨在典型激励下的敏感响应频率与显著波长对应的通过频率相近。

(3)有限元模型仿真计算结果与现场轨道振动特性测试结果相一致，表明钢轨显著波长波磨与轨道结构振动特性中的钢轨垂向Pinned-pinned共振有关，次显著波长波磨与钢轨相对于轨道板的垂向弯曲共振有内在联系。

[1]YOSHIHIKO Sato，AKIRA Matsumoto，KLAUS Knothe. Review on Rail Corrugation Studies[J]. Wear，2002，253(Supplement 1/Supplement 2)：130-139.

[2]GRASSIE S L,KALOUSEK J.Rail Corrugation: Characteristics, Causes, and Treatments[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal Rail & Rapid Transit,1993,207(1)：57-68.

[3]OOSTERMEIJER K H. Review on Short Pitch Rail Corrugation Studies[J]. Wear, 2008, 265(9): 1231-1237.

[4]NIELSEN Jens C O, LUNDEÉN Roger, JOHANSSON Anders，et al. Train-Track Interaction and Mechanisms of Irregular Wear on Wheel and Rail Surfaces[J]. Vehicle System Dynamics，2003, 40(1/2/3)：3-54.

[5]温泽峰. 钢轨波浪形磨损研究[D]. 成都：西南交通大学，2006.

(WEN Zefeng. Research on Rail Corrugation [D]. Chengdu: Southwest Jiaotong University，2006. in Chinese)

[6]赵国堂. 无砟轨道线路钢轨磨耗及轨道结构影响分析研究[R]. 北京：京沪高速铁路股份有限公司，2012.

(ZHAO Guotang. Study on the Cause and Effect of Rail Corrugation on High Speed Railway Slab Track[R]. Beijing: Beijing-Shanghai High Speed Railway Ltd. 2012. in Chinese)

[7]谷永磊，赵国堂，金学松，等.高速铁路钢轨波磨对车辆—轨道动态响应的影响[J].中国铁道科学, 2015，36(4):27-31.

(GU Yonglei, ZHAO Guotang，JIN Xuesong，et al. Effects of Rail Corrugation of High Speed Railway on Vehicle-Track Coupling Dynamic Response[J]. China Railway Science， 2015，36(4):27-31. in Chinese)

[8]刘钰，赵国堂.CRTSⅡ型板式无砟轨道结构层间早期离缝研究[J].中国铁道科学, 2013，34(4):1-7.

(LIU Yu,ZHAO Guotang.Analysis of Early Gap between Layers of CRTS Ⅱ Slab Ballastless Track Structure[J]. China Railway Science， 2013，34(4):1-7. in Chinese)