无砟轨道空间杆系动力分析模型

刘海涛

(中国铁道科学研究院 铁道建筑研究所，北京　100081)

无砟轨道动力分析通常采用梁—板模型[1-3]、梁—实体模型[4-8]和叠合梁模型[9-10]。叠合梁模型虽然结构简单，但目前仅能将轨道板模拟为纵向和竖向的二维结构，无法进行考虑横向的三维计算。梁—板和梁—实体模型在模拟钢轨与轨道板的连接时通常直接采用弹簧—阻尼，当采用单轴列车荷载加载模式时，轨道板上容易出现应力集中现象。图1为采用梁—板模型计算的轨道板应力云图。由图1可见，弹簧连接处轨道板的应力约为周围的2倍。图2为采用梁—实体模型计算的轨道板位移云图。由图2可见，弹簧连接处轨道板的位移为周围节点的10倍，并出现局部上翘的失真现象。而当采用垫板加多弹簧的方法模拟扣件系统对作用力的分散作用时，将使动力模型更为复杂。梁—板和梁—实体模型本身自由度数多，当进行大型计算时(如车辆—轨道—大跨度桥耦合系统计算)，需花费大量时间，计算1种工况甚至需要几十个小时[11]，当耦合恶劣条件时(如强风或地震)，由于系统的庞大，数值模拟甚至难以开展。因此有必要在满足精度要求的情况下，建立较为简化的无砟轨道动力分析模型，以便进行轨道结构或耦合系统的动力分析。

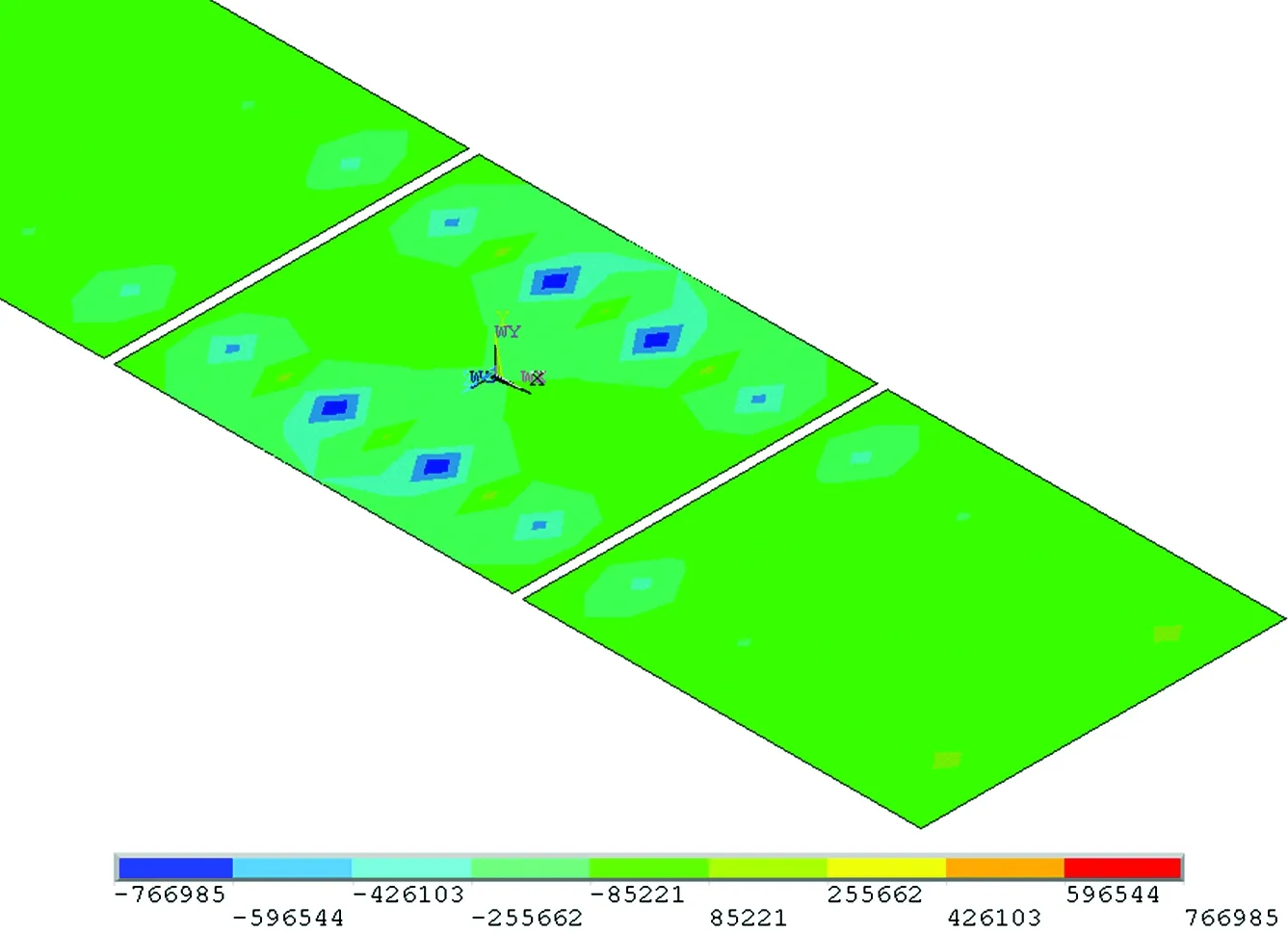
图1　梁—板模型下的轨道板应力云图

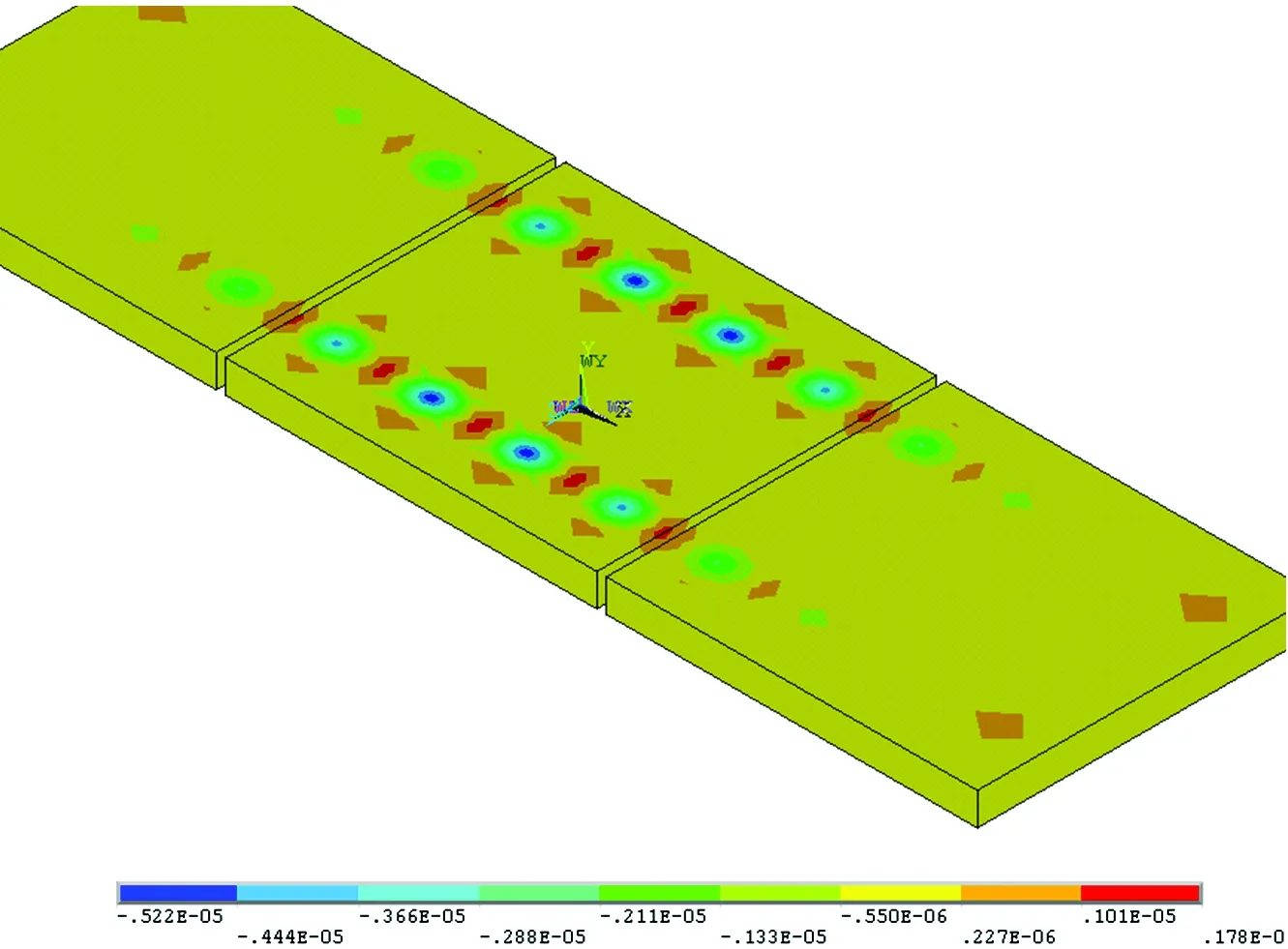
图2　梁—实体模型下的轨道板位移云图

本文采用“梁格”和“鱼骨梁”模拟无砟轨道系统的板式结构，将叠合梁模型进一步发展为空间杆系动力分析模型。以同一种典型轨道结构为研究对象，建立梁—梁格空间杆系、梁—鱼骨梁空间杆系和梁—实体3种无砟轨道空间动力分析模型，通过静、动力性能检验，验证空间杆系模型在无砟轨道动力分析中的可靠性。

1　无砟轨道结构动力分析模型

无砟轨道结构系统通常由钢轨、扣件、轨道板、底座和填充层等组成。以图3所示的1种典型单元式无砟轨道结构为分析对象(钢轨为60 kg·m-1轨，扣件间距0.7 m，轨道板厚0.24 m，单块板含4组扣件，轨道板长2.73 m，轨道板下为弹性支撑，采用中心限位结构)，分别采用实体单元法、梁格法和鱼骨梁法建立轨道结构动力分析模型。3种模型中钢轨均采用欧拉梁单元，钢轨与单元板之间采用弹簧阻尼体系连接。在实体单元模型中，轨道板采用实体单元模拟，轨道板下为均匀弹性支撑，扣件系统采用多弹簧与铁垫板综合模拟，其动力分析模型如图4所示。在梁格模型中，根据轨道结构的受力特点，轨道板在纵向对应每根钢轨离散为2根纵梁，在横向对应每组扣件分别建立相应横梁，赋予纵梁和横梁截面特性[12]，梁格下为离散弹性支撑，其动力分析模型如图5所示。在鱼骨梁模型中，每块轨道板采用1根纵梁模拟，轨道板上与钢轨相连的节点与纵梁间采用刚臂连接，纵梁为鱼骨，刚臂为刺梁，纵梁下为离散弹性支撑，其动力分析模型如图6所示。

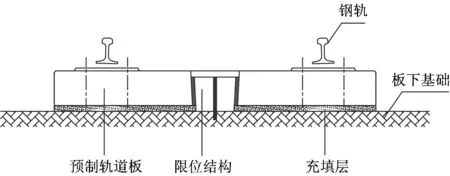
图3　轨道结构断面图

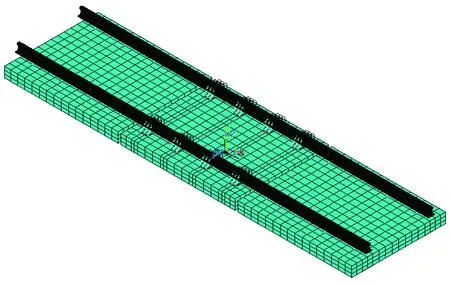
图4　轨道结构的实体模型

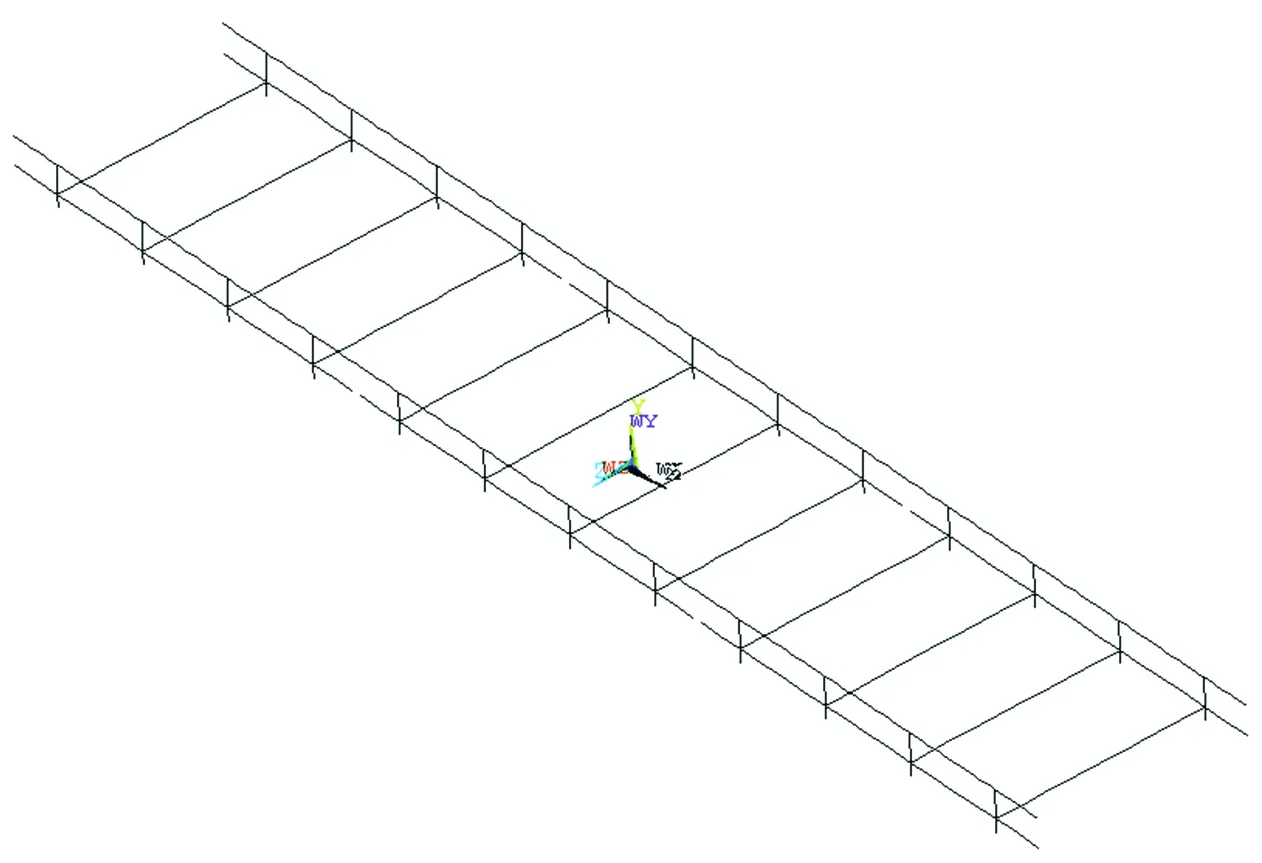
图5　轨道结构的梁格模型

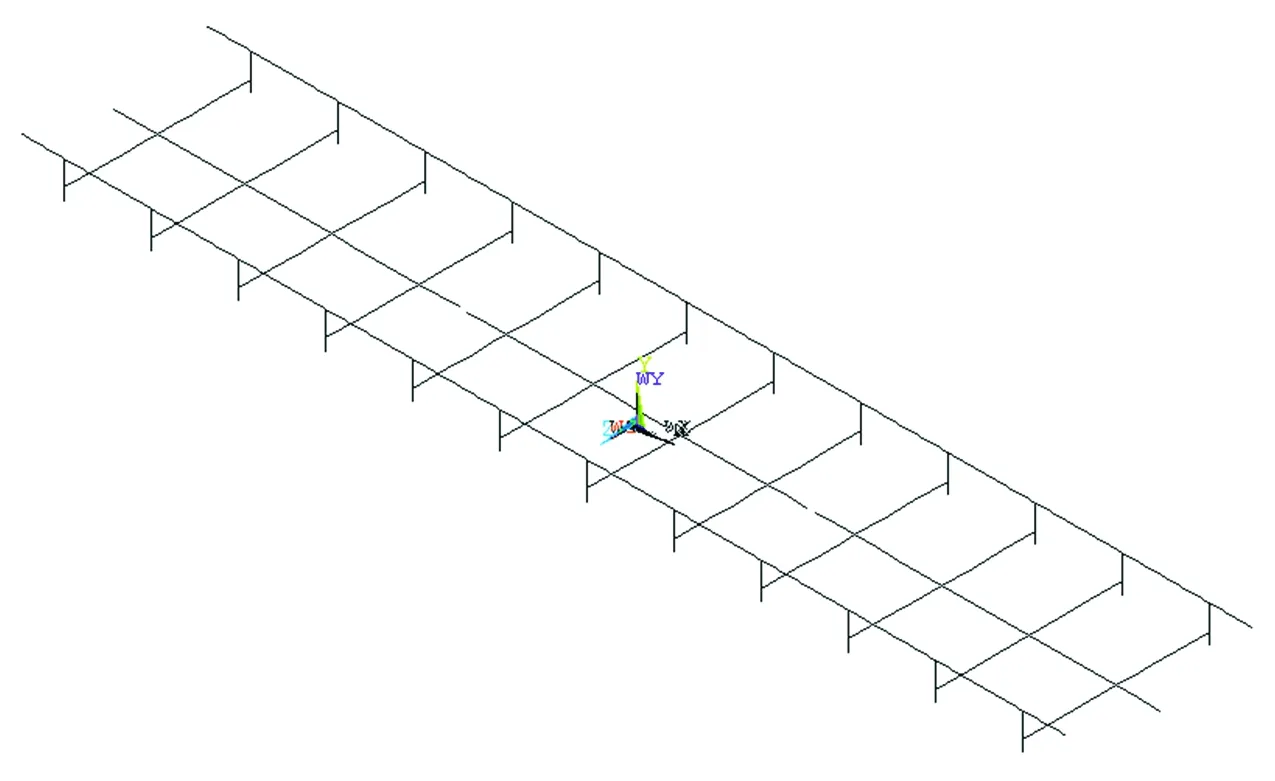
图6　轨道结构的鱼骨梁模型

2　无砟轨道结构静力分析

2.1　静载下各模型计算值

分别对3种模型施加单轴荷载，单轴加载又分为2轮对称加载和2轮偏载。对称加载时，左右轮荷载均为240 kN；偏载时，左轮荷载为240 kN，右轮荷载为120 kN。单块轨道板内的4组扣件从轨道板一端起编号依次为1#—4#扣件。轴载施加在钢轨上的位置分别对应轨道板板中、2#扣件和板端1#扣件。实体模型中轨道板应力取截面板底平均值，鱼骨梁模型中轨道板位移考虑板的扭转。对称和偏载加载时的计算结果分别见表1和表2。

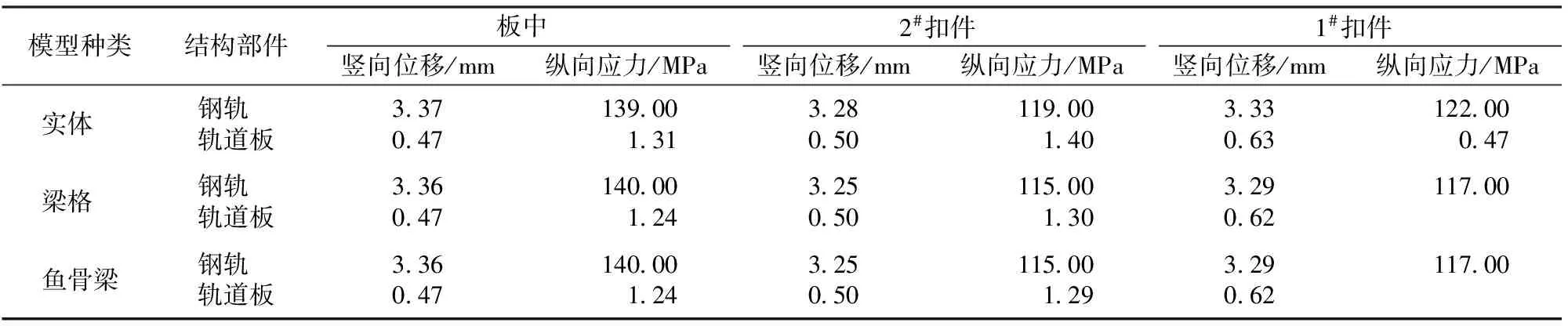
表1　对称加载时各模型计算的位移和应力

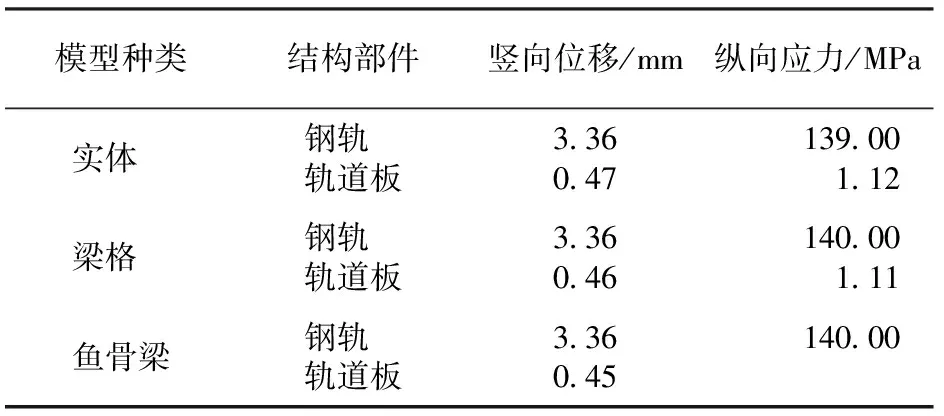
表2　偏载加载时各模型计算的板中位移和应力

由表1和表2可见：3种模型的计算结果基本一致；对称加载和偏载加载计算结果的规律基本一致；在1#扣件、2#扣件和板中位置加载时，钢轨及轨道板位移一致，位移最大差小于2%，应力最大差小于7%，即小于0.12 MPa。

采用单位轮重1 kN，分别得到3种模型板中截面轨道板和钢轨位移影响线，如图7和图8所示。由图7和图8可见， 3种模型计算得到的钢轨及轨道板的位移影响线基本重合。

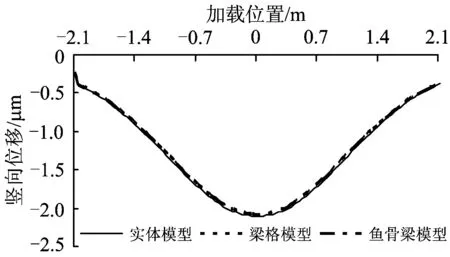
图7　板中处轨道板影响线

图8　板中处钢轨影响线

2.2　静载下计算值与试验值对比

在室内进行单块轨道板实尺模型的静载试验，荷载作用下的室内实尺模型如图9所示。对板中分别施加160，240，320和384 kN的荷载，测试不同荷载下轨道板的变形。表3给出了不同荷载下轨道板位移的试验结果和采用梁格模型的计算结果。由表3可见，实尺模型试验值与空间杆系模型计算值较为吻合，在加载点2#扣件处的位移最大相差0.03 mm。

图9　单块轨道板室内试验

轴载/kN1#扣件处2#扣件处3#扣件处4#扣件处试验值/mm计算值/mm试验值/mm计算值/mm试验值/mm计算值/mm试验值/mm计算值/mm160024017020017012012008003240032026027026017018011004320040035033034020024014006384046042039041023028016007

3　无砟轨道结构动力性能分析

采用3种模型分析无砟轨道动力特性、谐响应和瞬态动力响应。

3.1　无砟轨道结构的动力特性

表4为采用3种模型计算得到的轨道结构前7阶自振频率。图10给出了3种模型计算得到的1阶自振模态。由表4可见：3种模型得到的竖向和纵向自振频率相同，模态一致；3种模型得到的横向模态一致，实体和梁格模型得到的横向自振频率差别不大，分别为99和100 Hz，鱼骨梁模型得到的横向自振频率略小，为93 Hz。梁格模型比鱼骨

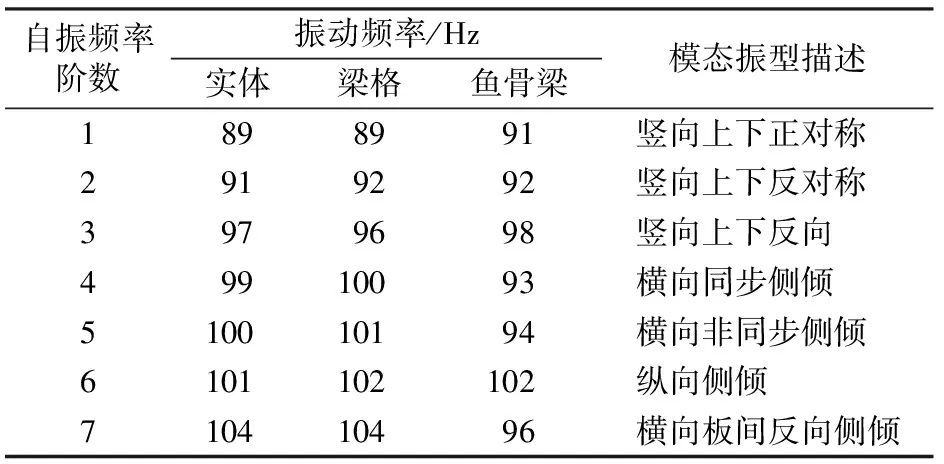
表4　不同模型计算得到的自振频率

梁模型更能精准地分析无砟轨道结构的横向动力性能。

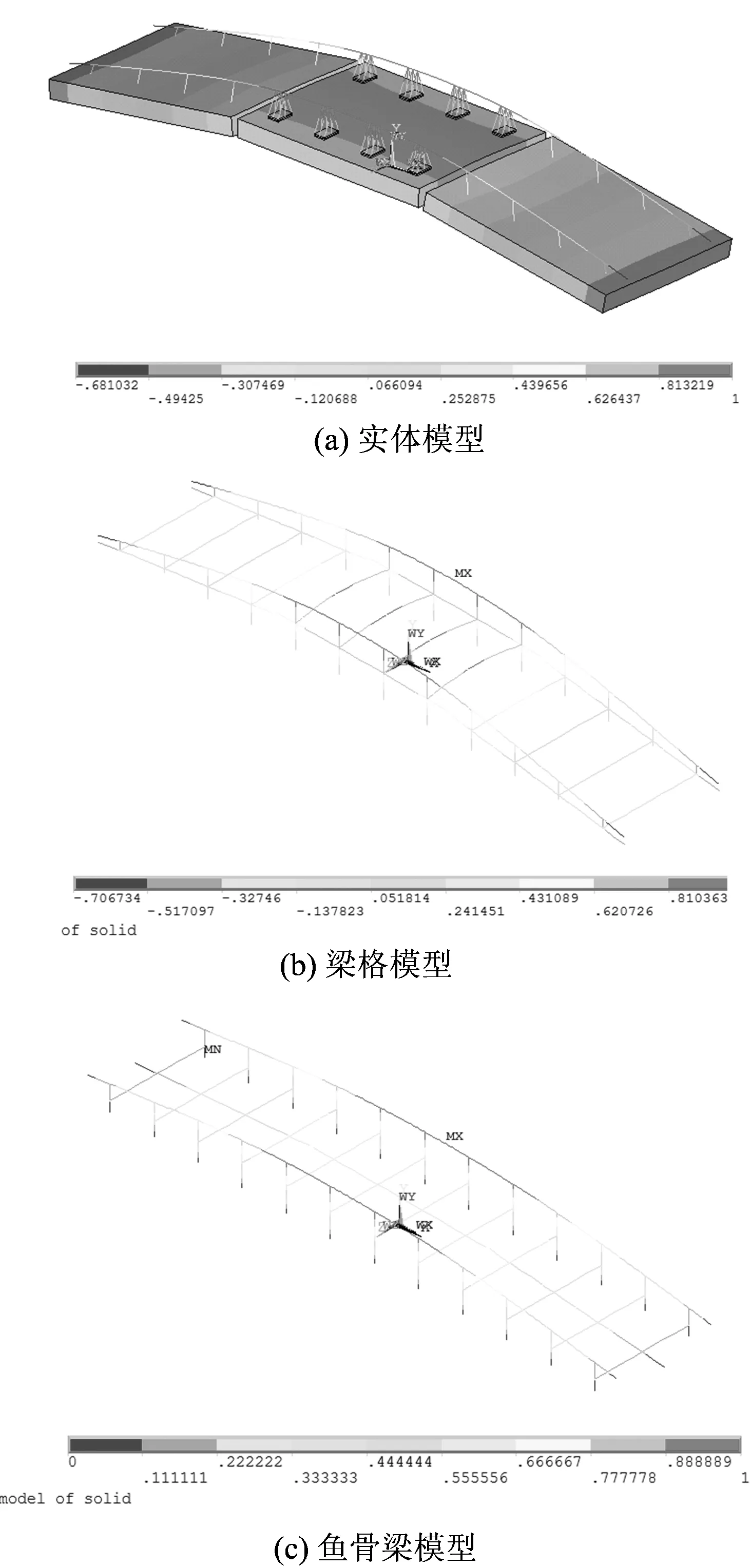
图10　3种模型计算得到的1阶自振模态

3.2　无砟轨道结构的谐响应分析

在轨道板板中对应钢轨上施加单位轮重1 kN，进行无砟轨道谐响应分析。图11、图12和图13分别为采用实体、梁格和鱼骨梁模型计算的垂向位移导纳图。由图11、图12和图13可见，3种模型的谐响应基本一致。

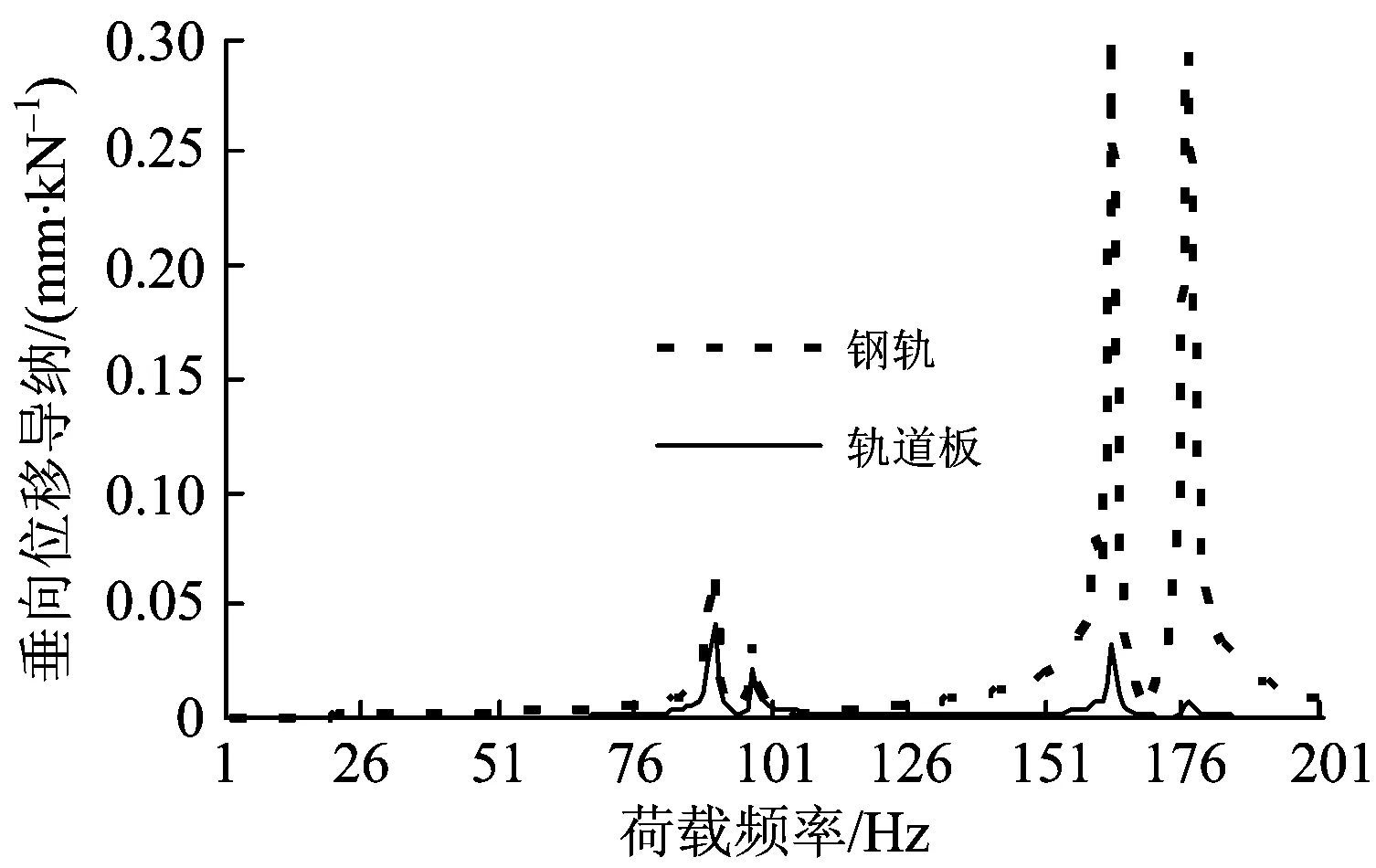
图11　采用实体模型计算得到的垂向位移导纳

表5为根据垂向位移导纳图确定的轨道结构自振频率。由表5可见，3种模型确定的自振频率差别不大，1阶频率分别为90，92和91 Hz。谐响应确定的结构竖向自振频率与表4中的竖向自振频率相比，2种方法得到的竖向自振频率相近。

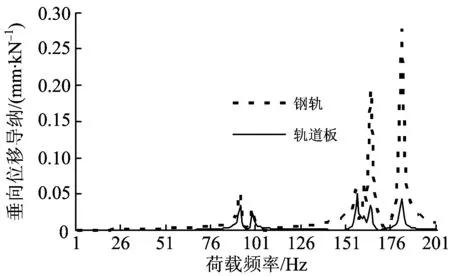
图12　采用梁格模型计算得到的垂向位移导纳

图13　采用鱼骨梁模型计算得到的垂向位移导纳

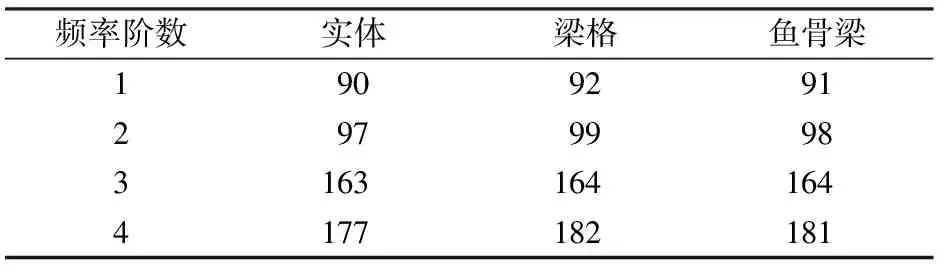
Hz

3.3　无砟轨道瞬态动力分析

分别采用3种模型进行移动力加载下的无砟轨道瞬态动力分析，研究移动力作用下这3种模型计算结果的差异。移动力采用单轴加载方式，轮重取120 kN，速度为90 km·h-1。图14、图15和图16分别给出了采用3种模型分析得到的板中处钢轨和轨道板竖向位移的时程曲线。计算结果表明，移动力作用下实体、梁格和鱼骨梁模型计算的轨道结构变形一致。

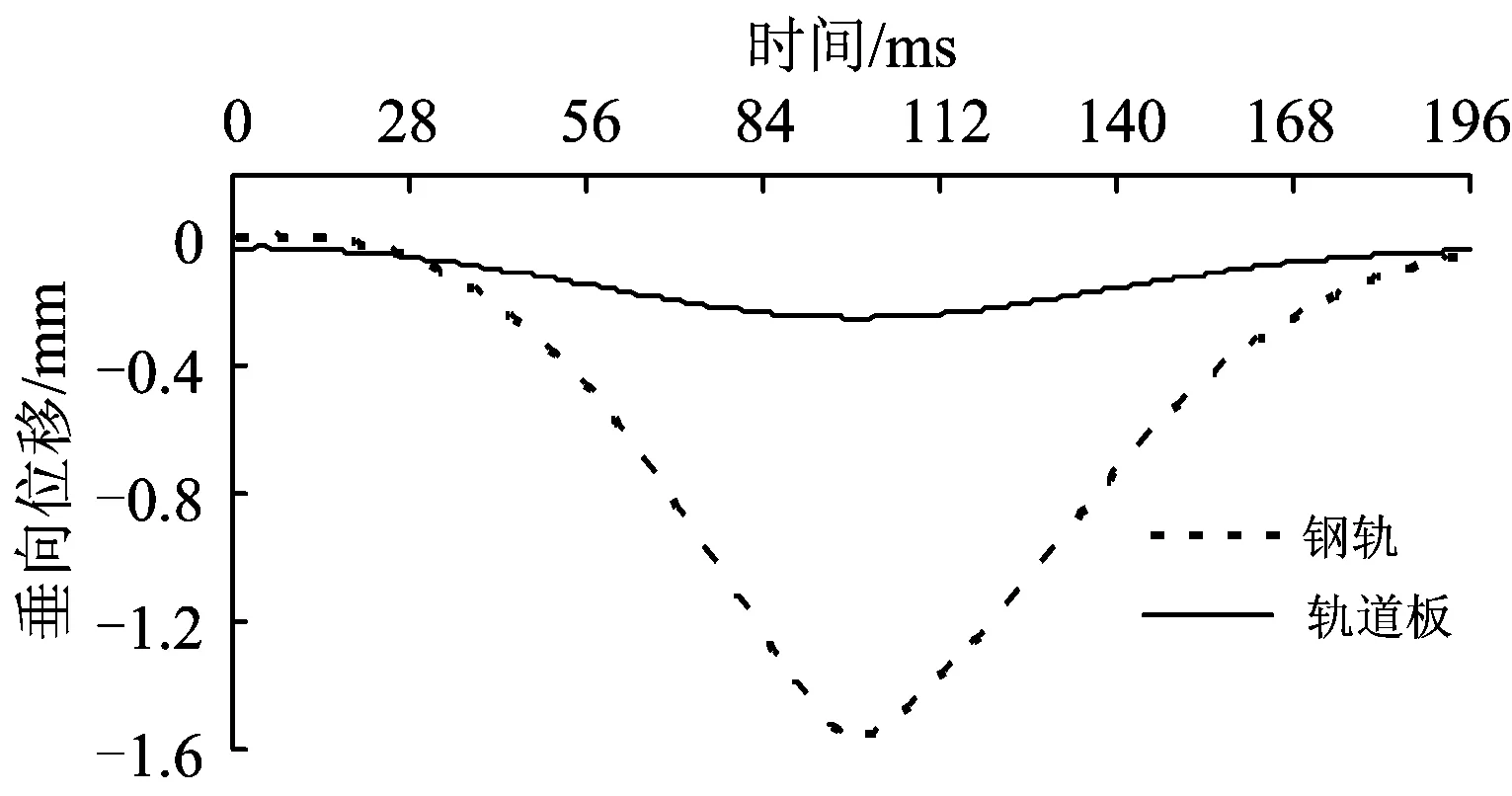
图14　采用实体模型计算得到的垂向位移

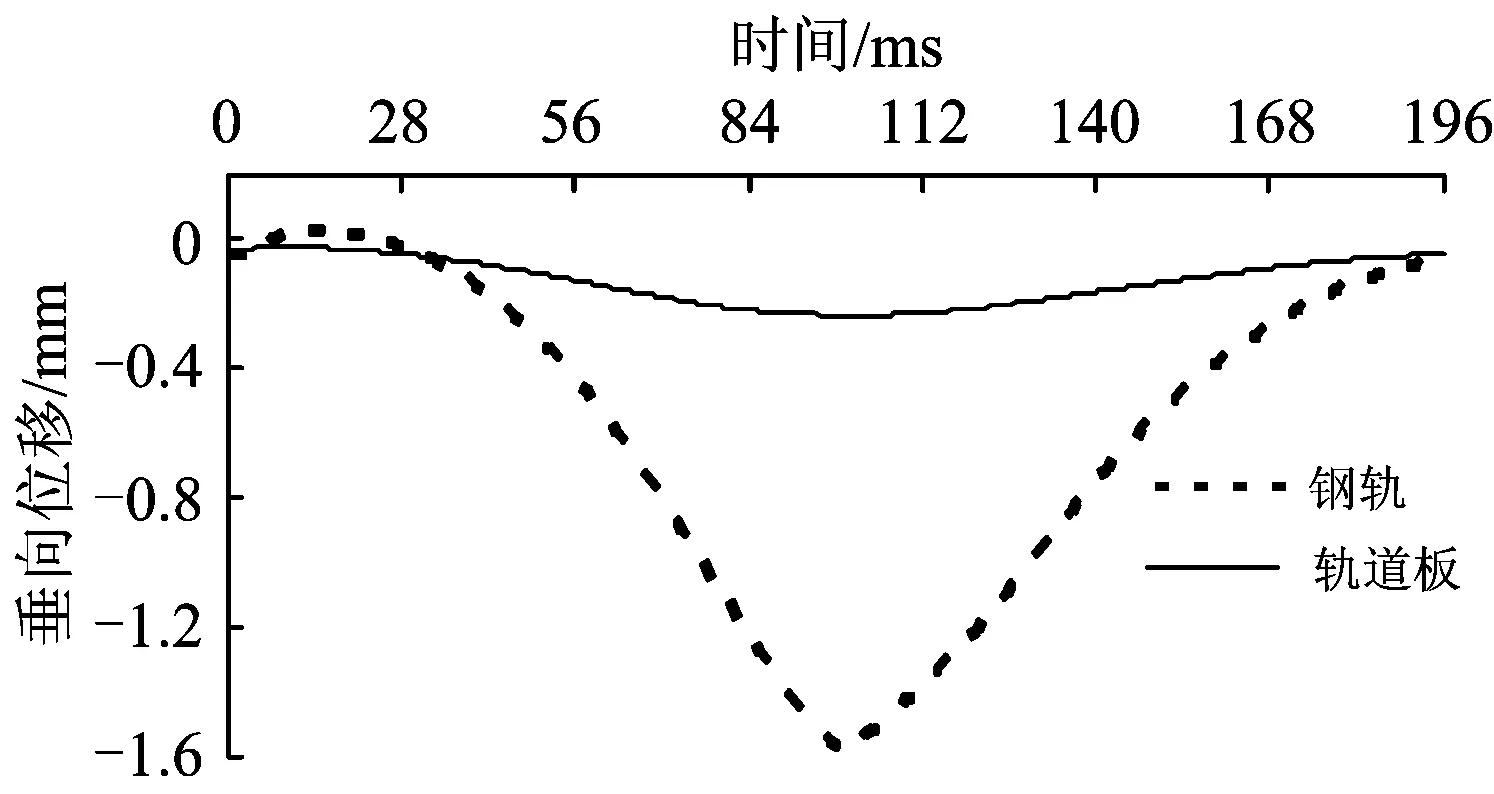
图15　采用梁格模型计算得到的垂向位移

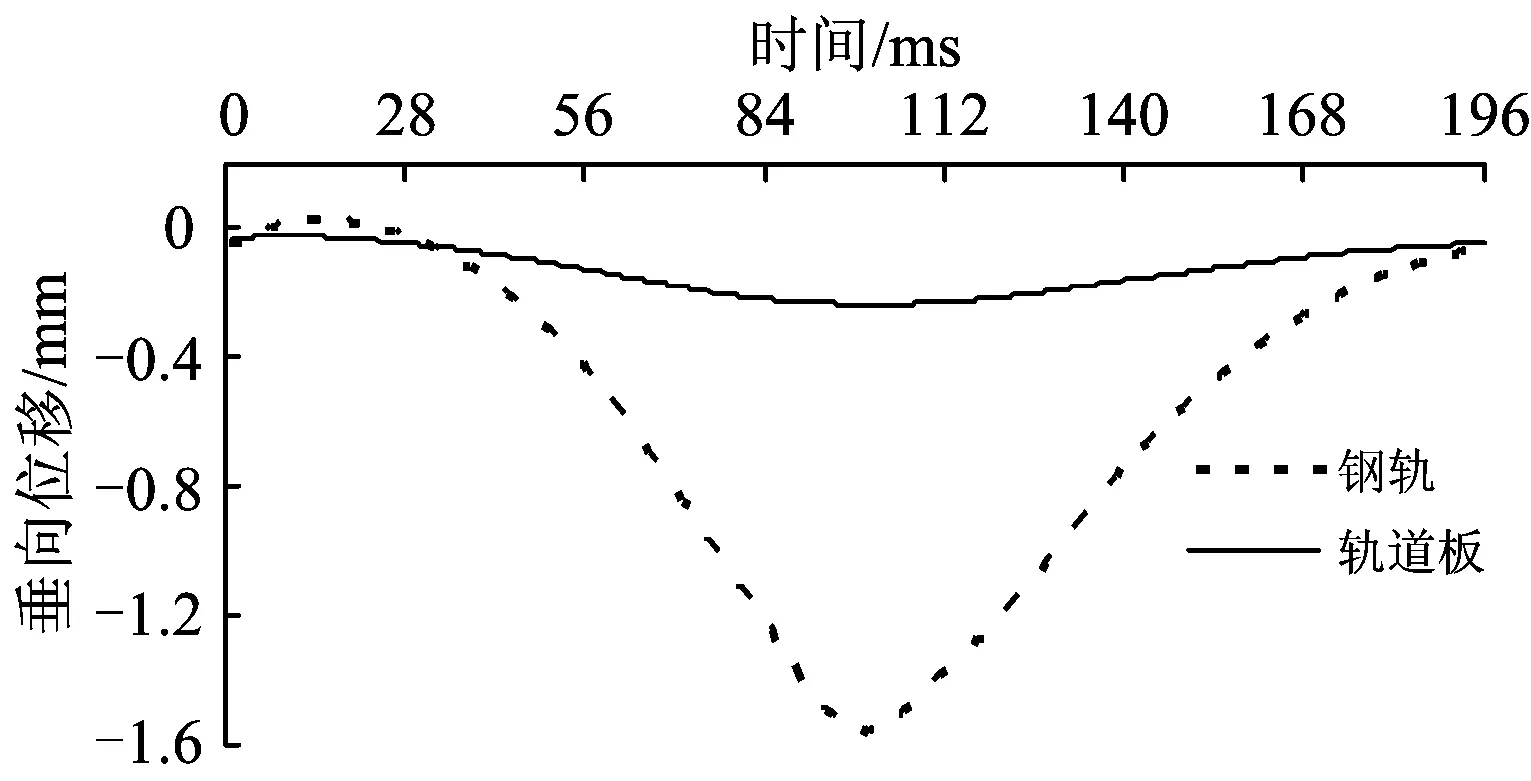
图16　采用鱼骨梁模型计算得到的垂向位移

4　梁—梁格模型与梁—实体模型计算效率比较

空间杆系模型结构简单，可采用弹簧—阻尼直接模拟扣件系统，建模方便。在单元大小接近的情况下，分别采用梁格法和梁—实体单元法建立28 m长度的钢轨—轨道板动力分析模型，采用单轴荷载、运用同一电脑，进行700步移动力瞬态动力分析，梁格模型的计算时间为10 min，梁—实体模型的计算时间为80 min，对于此类简单计算，

梁—梁格模型的计算效率已是梁—实体模型的8倍，对于大型动力分析，梁格模型的计算效率优势将更加突出。

5　结　论

(1)在板中施加对称和非对称荷载以及板端施加对称荷载条件下，采用空间杆系模型和精细化模型计算的钢轨和轨道板位移和应力基本一致；位移最大差小于2%，应力最大差小于7%，即小于0.12 MPa；由3种模型得到的影响线基本一致。

(2)不同荷载条件下采用梁—梁格模型计算的轨道板位移与实测结果基本吻合，加载点处轨道板位移的最大差为0.03 mm。

(3)空间杆系模型和精细化模型对无砟轨道结构的竖向动力性能分析方面具有相同的精度，梁—梁格模型比梁—鱼骨梁模型更能精准地分析无砟轨道结构的横向动力性能。

(4)梁—梁格模型比梁—实体模型具有更高的计算效率。对于一段长28 m的无砟轨道，采用梁—梁格模型的计算效率为采用梁—实体模型的8倍。

(5)梁—梁格模型比梁—鱼骨模型具有更好的横向动力性能，且比梁—实体模型、梁—梁板模型建模方便，自由度数少，计算效率高。梁—梁格模型可应用于轨道结构的动力分析，尤其是车—线—桥多工况和长大列车编组的庞大系统分析。

[1]TANABE M, WAKUI H, MATSUMOTO N, et al. Dynamic Interactions of Shinkansen Train, Track and Bridge[C]//IABSE Symposium Report. Antwerp, Belgium: International Association for Bridge and Structural Engineering, 2003：10-16.

[2]O’ RIORDAN N, ROSS A, ALLWRIGHT R, et al. Long Term Settlement of Piles under Repetitive Loading from Train[C] //IABSE Symposium Report. Antwerp, Belgium: International Association for Bridge and Structural Engineering，2003：17-23.

[3]赵坪锐, 章元爱，刘学毅，等.无砟轨道弹性地基梁板模型[J]. 中国铁道科学，2009,30(3):1-4.

(ZHAO Pingrui, ZHANG Yuanai, LIU Xueyi, et al. Beam-Plate Model on the Elastic Foundation of Ballastless Track[J]. China Railway Science, 2009,30(3):1-4. in Chinese)

[4]STEENBERGEN M J M M, METRIKINE A V, ESVELD C. Assessment of Design Parameters of a Slab Track Railway System from a Dynamic Viewpoint [J]. Journal of Sound and Vibration, 2007, 306(1/2):361-371.

[5]SUIKER A S J, METERIKINE A V, DE BORST R. Steady State Response of a Granular Layer to a Moving Load-a Discrete Mode[J]. Heron, 2000, 45(1)：75-87.

[6]高亮，杨文茂，曲村，等.高铁长大桥梁CRTSⅠ型板式无砟轨道无缝线路的动力学特性[J]. 北京交通大学学报, 2013,37(1)：73-79.

(GAO Liang, YANG Wenmao, QU Cun, et al.Dynamic Characteristics of CRTSⅠSlab CWR Track on Long-Span Bridge in High-Speed Railway[J]. Journal of Beijing Jiaotong University, 2013,37(1)：73-79. in Chinese)

[7]石现峰，宣言，王澜. 土质路基上板式无砟轨道结构的动力学性能仿真研究[J].中国铁道科学，2008,29(4)：15-20.

(SHI Xianfeng, XUAN Yan, WANG Lan. Simulation Research on the Dynamics Characteristics of Slab Ballastless Track Structure on Soil Subgrade[J]. China Railway Science, 2008,29(4)：15-20. in Chinese)

[8]徐庆元，范浩，李斌. 无砟轨道温度梯度荷载对列车—路基上板式无砟轨道系统动力特性的影响[J]. 铁道科学与工程学报, 2013,10(3):1-6.

(XU Qingyuan，FAN Hao，LI Bin. Influence of Temperature Gradient Load of Slab on Dynamic Characteristic of Train-Slab Track on Subgrade System[J]. Journal of Railway Science and Engineering, 2013,10(3):1-6. in Chinese)

[9]翟婉明，韩卫军，蔡成标. 高速铁路板式轨道动力特性研究[J]. 铁道学报，1999,21(6): 64-69.

(ZHAI Wanming, HAN Weijun, CAI Chengbiao. Dynamic Properties of High Speed Railway Slab Tracks[J]. Journal of the China Railway Society,1999,21(6): 64-69. in Chinese)

[10]XIE W P, HU J W, XU J. Dynamic Response of Track-Ground Systems under High Speed Moving Load[J]. Chinese Journal of Rock Mechanics and Engineering, 2002,21(7)：1075-1078.

[11]刘海涛. 强风作用下列车—汽车—桥梁时变系统的动力响应及行车安全性、舒适性研究[D]. 长沙:中南大学, 2011.

(LIU Haitao. Dynamic Responses of Coupled Train, Automobile and Bridge System under Strong Wind and Analysis of Running Safety and Riding Comfort of Vehicles[D]. Changsha: Central South University, 2011. in Chinese)

[12]戴公连，李德建. 桥梁结构空间分析设计方法与应用[M].北京：中国交通出版社，2001.