高速铁路无砟轨道—路基变形计算模型的研究

赵国堂

(中国铁路总公司，北京　100844)

高速铁路的建造和养护维修必须要保证轨道的高平顺性和高稳定性。因此对路基工程不仅要求具有足够的强度，更重要的是还要有维持长期变形稳定的能力。但是，路基作为土工构筑物，除自身的长期流变性质外，外部荷载和水的作用也都会导致其变形不断累积，使得高速铁路严苛的沉降控制标准无法完全实现。在早期建造高速铁路的国家中，日本由于东海道新干线出现了部分路段路基沉降且难以修复的问题而迫使日本改变了新干线的技术路线，增大了桥梁比例[1]。在德国，科隆—法兰克福高速铁路于2002年开通运营，2004年出现了2段比较大的路基沉降，其中一段路基沉降的波长为200 m左右，最大沉降值为55 mm，另外一段路基沉降的波长为60 m左右，最大沉降值为42 mm，但道床板和支承层没有可见的伤损；另一条汉诺威—柏林高速铁路也出现了路基沉降，其波长为40 m左右，最大沉降值为18 mm，且道床板和支承层均出现张开裂缝，经雷达检测表明，路基本体也出现了裂缝，不得不采用注浆措施加以抬升和修复[2]。我国高速铁路的地质条件复杂，软土、松软土分布广，黄土、膨胀性岩土在一定区域内广泛存在，因此控制路基变形是一项非常重要的工作，特别是我国时速300 km及以上高速铁路全面采用无砟轨道，造成针对路基变形的维修十分困难。因此，研究路基变形对无砟轨道的影响具有重大的理论价值和现实意义。

目前，我国高速铁路运营里程已经超过19 000 km，铺设的无砟轨道达22 000 km以上。为确保路基上无砟轨道结构的安全、可靠，我国制定了严苛的路基沉降控制标准，要求其工后沉降在波长为20 m时不得超过15 mm，在波长为20 m以上时不得超过30 mm[3]；在无砟轨道结构设计中，统一了无砟轨道变形荷载的表征方式，建立了无砟轨道—路基变形的静态和动态分析模型[4-18]；在路基施工过程中，制定了严密的路基沉降观测与评估流程，要求在路基施工时建立完善的变形监测网，设置沉降观测桩和沉降板，一般情况下每50 m设置1个观测断面，对路基面沉降和地基沉降进行观测[19]，并根据观测数据，对路基工后沉降进行预测，只有在满足沉降控制标准的条件下才允许进行无砟轨道的施工。

路基的变形控制标准和观测评估流程是高速铁路建设阶段保证无砟轨道工程质量的重要依据，无砟轨道—路基变形计算模型是研究路基变形对无砟轨道影响的重要手段。目前的无砟轨道—路基变形计算模型除表征路基沉降统一采用余弦方程外，在边界条件、无砟轨道各结构层的层间关系等方面差异巨大。边界条件是结构计算分析中最基本也是最重要的条件，一旦出现错误或偏差，就无法得到正确的计算结果。现有计算模型中一般选择无砟轨道支承层或底座板与路基面交界的界面作为下部边界并输入变形激励[4-12,14,17]，或以基床表层底部作为边界并输入变形激励[13,18]；从一定意义上来说，这样并没有反映出路基工后沉降变形的机理。针对高速铁路，国内外的共识是，在铺设无砟轨道时路基本体的变形已经完成，工后沉降主要是由地基沉降引起的；因此，一般情况下计算模型的下部边界应以路基本体与地基交界的界面为宜，只有在分析路基本体病害对轨道影响时，才应选择路基面为下部边界。无砟轨道各结构层的层间关系是分析路基变形对轨道影响的基础，而现有计算模型中采用的梁—板—弹簧阻尼结构并不能模拟各结构层之间的接触状态；采用实体单元时，将各结构层的层间关系用接触单元模拟[7,10-17]，可以模拟出路基变形向钢轨传递以及各结构层的变形和受力状况；而按结合良好进行模拟[5,6,8，9,18]则无法反映层间的作用。

因此，作者提出基于路基工后沉降变形的机理和无砟轨道各结构层的层间关系构建高速铁路无砟轨道—路基变形计算模型，以建立的双块式无砟轨道—路基变形计算模型为例，通过对比分析不同边界条件、层间关系的处理结果，验证所提出模型的合理性和可靠性。

1　轨道—路基变形计算模型的构建

路基一般由路基本体和地基2部分组成，其中路基本体又分为基床表层、基床底层和基床以下路堤等3部分，如图1所示。一般认为，路基本体在铺设无砟轨道时其性能已经稳定，路基工后沉降变形主要由地基变形引起。因此，合理的轨道—路基变形计算模型的下部边界应为路基本体的底部，这一方面符合路基工后沉降变形的机理，另一方面路基本体的初始参数是确定的，可以根据设计和施工状况进行选取。考虑的路基填料为散粒体，其层间可按变形连续处理。

路基变形对无砟轨道结构的影响，主要体现在路基的变形通过无砟轨道结构向钢轨传递，从而引起轨道不平顺的变化；路基变形会对无砟轨道的稳定性产生影响，比如CRTSⅡ型板式无砟轨道的轨道板和双块式无砟轨道的道床板均没有限位结构，前者的稳定主要依靠轨道板与CA砂浆层之间的黏结性能，后者的稳定主要依靠道床板与支承层之间的摩阻力，路基变形将会引起轨道板与CA砂浆层以及道床板与支承层之间出现离缝、脱空，从而打破无砟轨道结构体系的稳定，可能会引起结构的失稳；路基变形还会导致无砟轨道结构的伤损，如轨道板、道床板、底座板、支承层出现裂缝，板下充填层出现破损等。无砟轨道结构总体上均是层状结构，在构建无砟轨道—路基变形计算模型时，无砟轨道各结构层之间按层间接触处理，才能够反映各结构层抵抗变形和受力的特点，模拟路基变形对轨道不平顺、无砟结构稳定和伤损的影响。

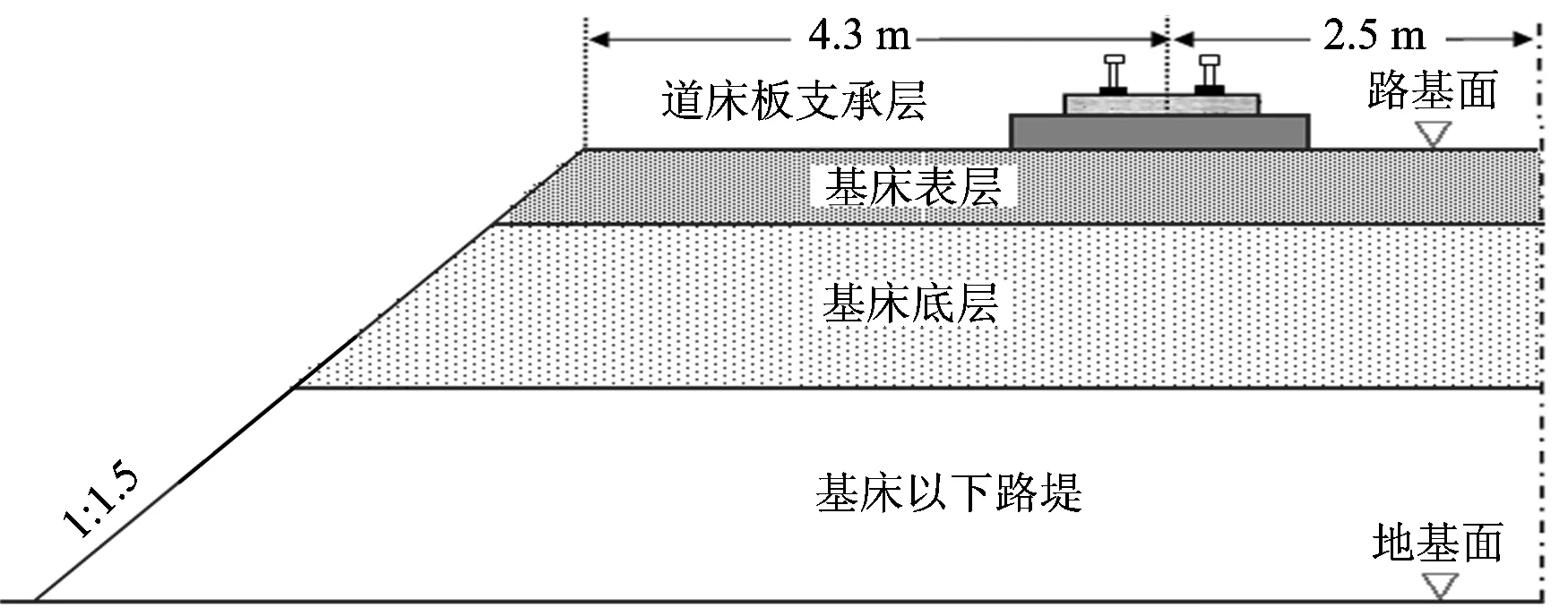
图1　轨道与路基结构断面图

底座板或支承层与路基面之间按层间接触进行模拟，地基系数用非线性弹簧进行模拟，路基变形的波形采用如图2所示的单波余弦曲线表示，其表达式为

(1)

式中：f0为波峰；Z为不均匀沉降的位置坐标；l为波长。

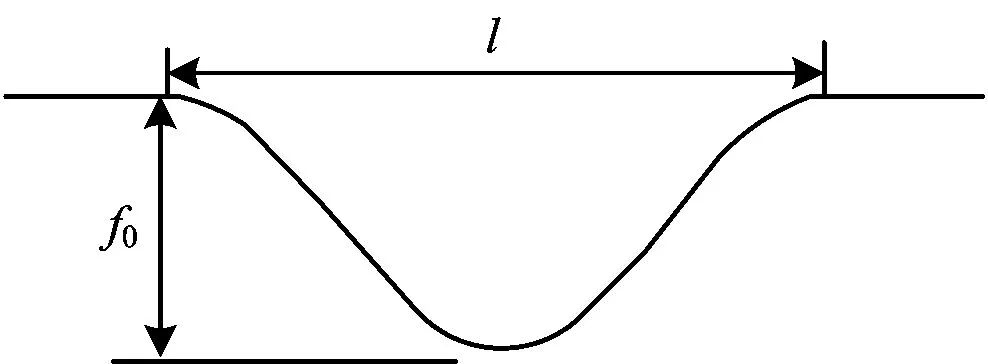
图2　余弦型沉降曲线

为研究计算模型下部边界条件的影响，在本文建立的双块式无砟轨道—路基变形计算模型中，下部边界分别取如图1所示的路基面和地基面2类边界条件；另外，道床板与支承层间按层间接触和层间结合2种情况考虑；钢轨采用梁单元模拟，道床板、支承层和路基均采用空间实体单元模拟；道床板和支承层为线弹性材料，路基选用Mohr-Coulomb材料；扣件及路基表面弹性均采用弹簧单元模拟；为简化计算，层间接触时的摩擦系数均取0.5。

采用ABAQUS软件对双块式无砟轨道—路基变形计算模型进行有限元计算，路基变形波长的计算范围为5～120 m，变形幅值的计算范围为10～50 mm。钢轨为60 kg·m-1级，扣件的静刚度取30 kN·m-1，节点间距取625 mm，其他输入参数见表1。

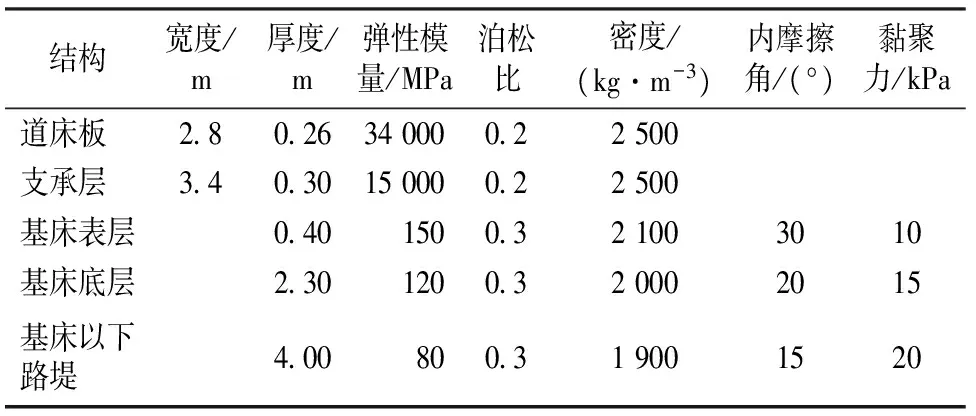
表1　基本参数取值

2　计算结果及其分析

为便于表述，将轨道变形波长与在地基(或路基)面上输入的变形波长之比称为波长传递比，将轨道变形幅值与在地基(或路基)面上输入的变形幅值之比称为幅值传递比。

2.1　下部边界条件的影响

应用道床板与支承层为层间接触的计算模型对下部边界条件分别为地基面和路基面2种情况进行计算分析。

(1)当下部边界为地基面时，如图3所示(图中：LF，AF分别为在地基面上输入的变形波长和幅值；变形等值线上数字的单位为mm。图中显示出4层结构，自上而下依次为道床板、支承层、路基基床、基床以下路堤)，在地基面上的变形通过路基本体向轨道结构传递的过程中，形成路基本体和轨道变形波长逐渐增大的沉降漏斗。当LF较小时，所引起轨道变形的波长增加和幅值减小均比较明显；而当LF较大时，对应的轨道变形波长有所增大，但幅值逐步向上传递。

地基面变形的传递可用传递比来表示，如图4所示(图中：LR，AR分别为轨道变形的波长和幅值)。由图4(a)可以看出，波长传递比与LF成反比，而与AF成正比。由波长传递比可以推算出，地基变形所引起的轨道不平顺一般为长波不平顺(波长在30 m以上)，此结论与长期以来形成的轨道长波不平顺产生机理相一致。另外，从图4(b)可以看出，幅值传递比受LF影响显著，随着LF的增大逐渐趋近于1，但受AF的影响很小，并且3个AF值下得到的3条幅值传递比变化曲线高度重合。这说明，当LF较小时，路基本体随地基的变形而产生相应的变形，即当AF增大时，路基本体的变形量也随之增大，则传递到轨道时轨道变形的波长也同样随之增大，但幅值增加量很小，从而形成波长传递比增大和计算条件下幅值传递比曲线高度重合的结果；当LF较大时，路基本体与地基变形的跟随性增强，传递到轨道时轨道变形的波长和幅值的增加量均很小，使得轨道变形的波长和幅值与LF和AF逐步接近。从本文计算条件得到的结果可以认为，LF达到60～80 m时，波长和幅值的传递比接近于1，轨道变形与地基变形基本一致。

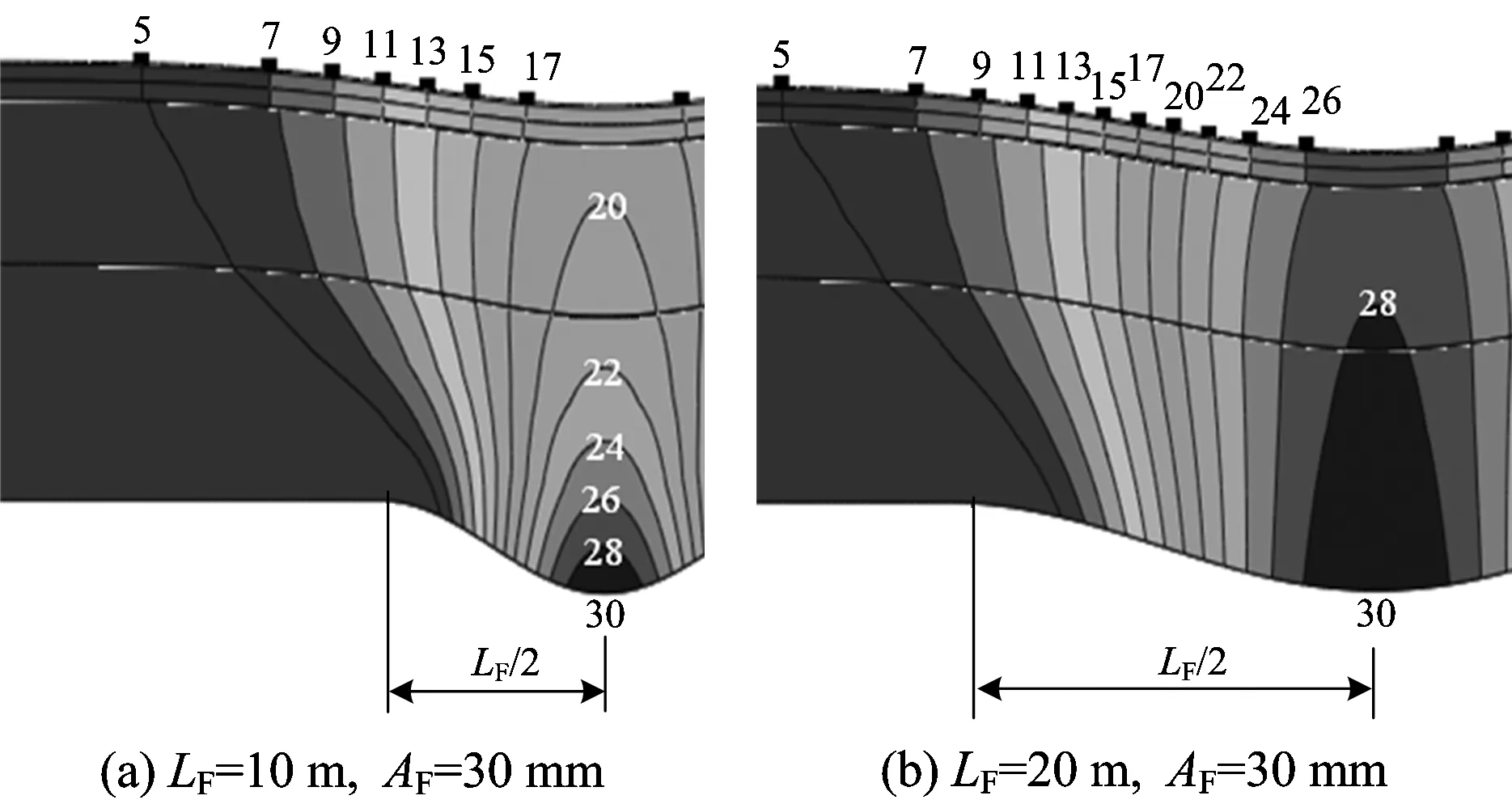
图3　下部边界为地基面时路基和轨道的变形等值线图

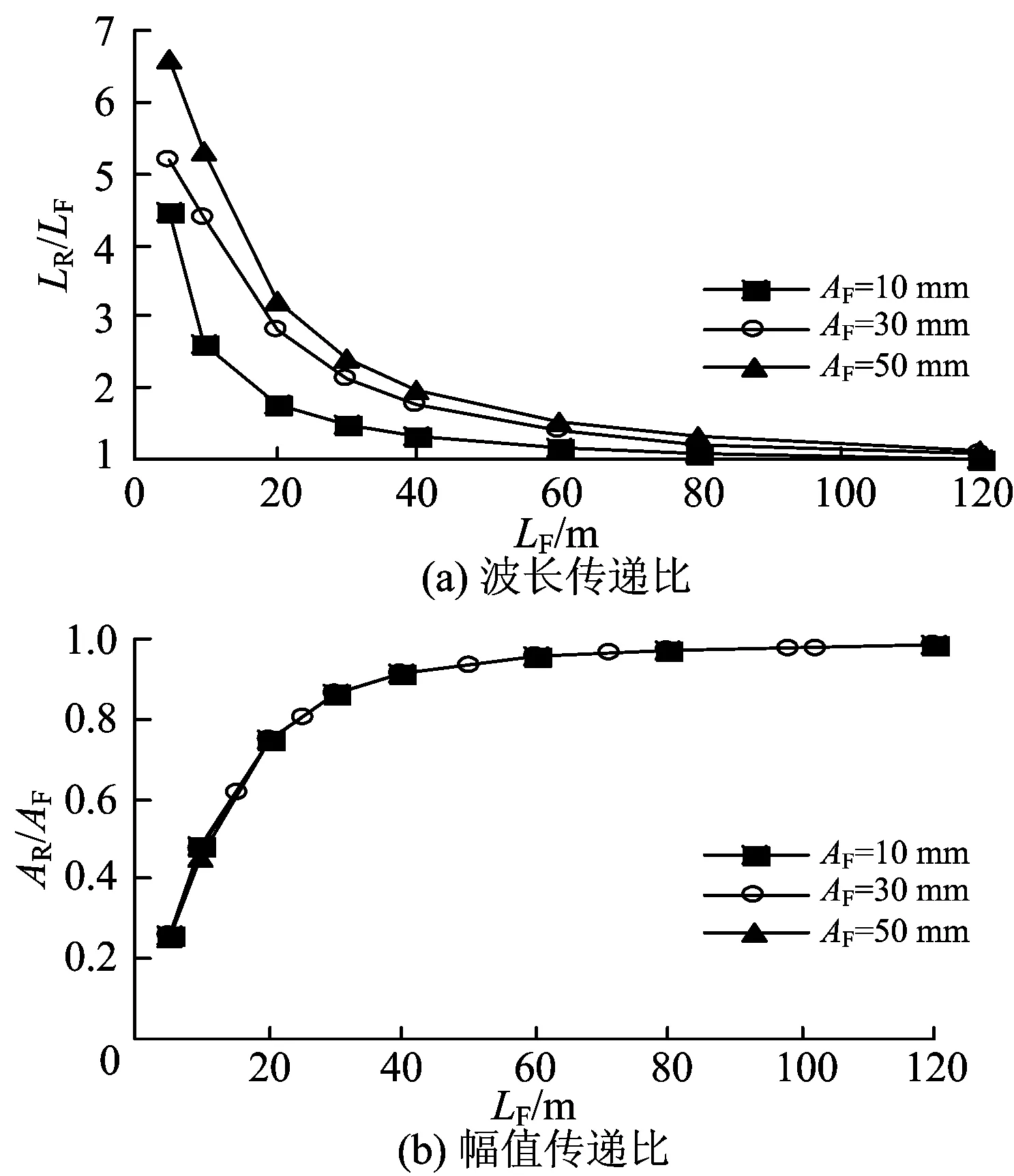
图4　下部边界为地基面时波长和幅值的传递比计算结果

(2)当下部边界为路基面时，如图5所示(图中：LS，AS分别为在路基面输入的变形波长和幅值，变形等值线上数字的单位为mm。图中显示出2层结构，自上而下依次为道床板和支承层)，计算模型中的轨道结构层只有支承层和道床板2层，在支承层的底部输入一定波长和幅值的变形以后，由于道床板的抗弯刚度较支承层大，故当路基面变形的波长较小时，道床板的挠曲变形较小，导致道床板与支承层之间产生离缝，使得传递到钢轨的变形幅值减小；当路基面变形的波长增大到一定值以后，道床板挠曲变形随之增大，与支承层的变形跟随性增强，离缝逐渐减小，轨道变形逐步与路基面一致。

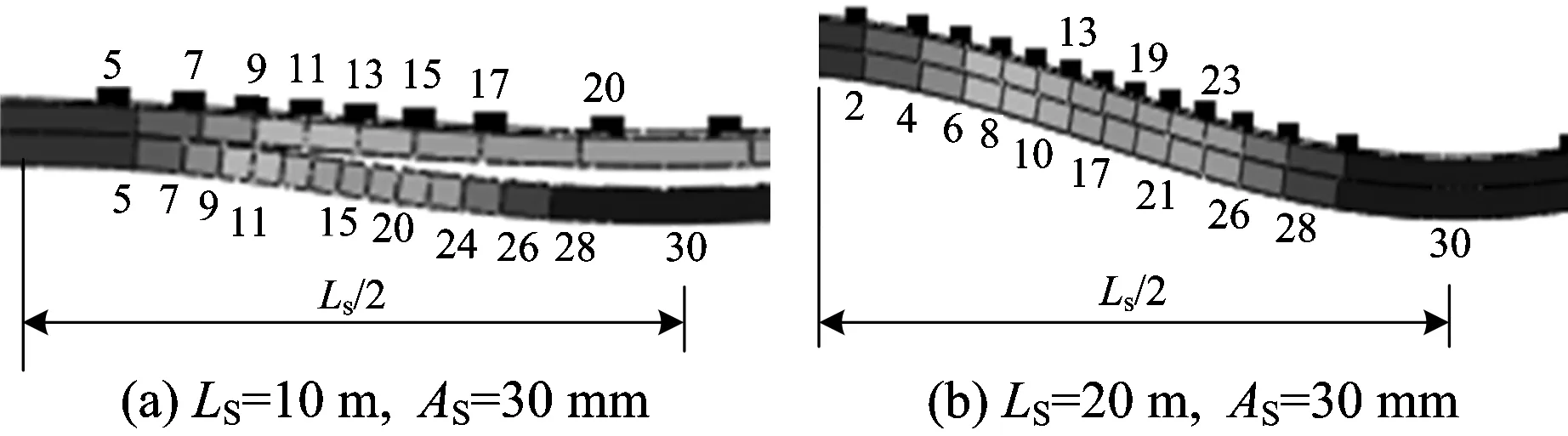
图5　下部边界为路基面时轨道变形等值线图

路基面变形的传递同样可用如图6所示的传递比来表示，传递比的变化规律与图4所示相似，但是在输入相同的变形波长和幅值的条件下，波长传递比：前者达到1～7，后者只有1～2，这说明路基面变形对轨道变形波长的影响很小；幅值传递比：前者在60～80 m变形波长以内时变化比较缓慢，后者在30 m变形波长以内时快速增大并接近1。

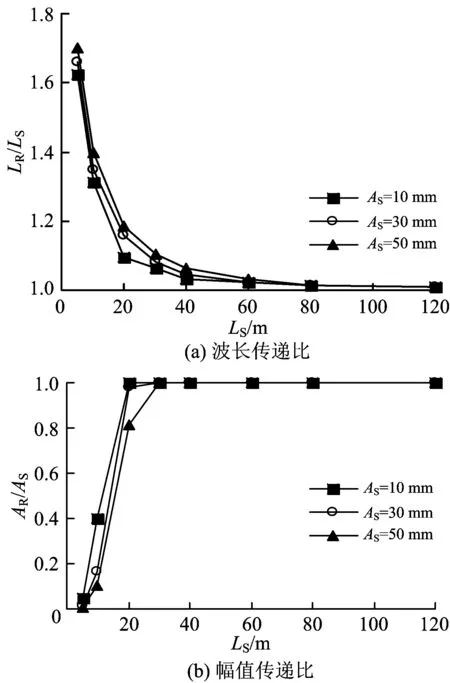
图6　下部边界为路基面时波长和幅值的传递比计算结果

对比以上2种边界条件下波长和幅值传递比的差别，主要是无砟轨道与路基之间的关系有所不同。下部边界为地基面时，无砟轨道是主动适应和协调与路基面的关系，由于地基面上的变形传递到无砟轨道底部时波长增大、幅值减小，因此无砟轨道的变形比较“柔和”；而下部边界为路基面时，支承层承受的是“强制性”变形荷载，即路基面输入余弦型变形荷载后，支承层必须产生与输入变形波长和幅值相同的变形，道床板在适应和协调与支承层的关系时，由于其材料特性和结构尺寸的限制，只能够通过产生离缝来减少路基变形幅值向钢轨的传递，对变形波长传递的影响很小。

这2种边界条件下的计算结果除传递比有差异外，还体现在当下部边界为路基面时，支承层承受着由“强制性”变形荷载所产生的与道床板的离缝及拉应力2个方面。如图7所示，在下部边界为路基面的条件下，当路基变形的波长较小时，道床板与支承层间的离缝很大，而且参照图5(a)，如果将道床板在支承层发生沉降变形后的状况视为一简支梁，则其最大挠度与路基变形波长的4次方成正比，与路基的抗弯刚度成反比；当路基变形的波长增大后，道床板的最大挠度也迅速增大，但与支承层间的离缝迅速减小，由此也可以揭示离缝迅速减小是幅值传递比突然增大的原因。

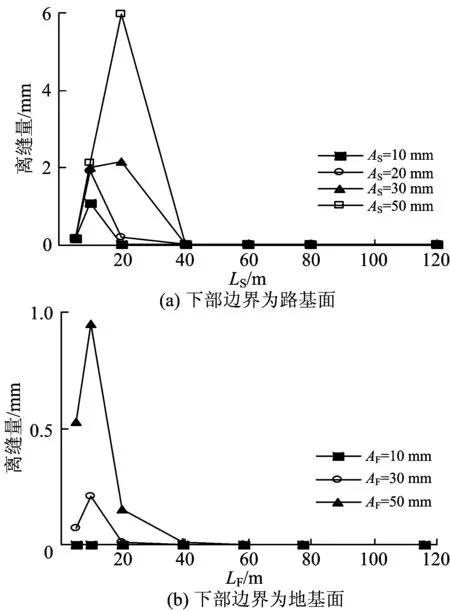
图7　道床板与支承层间的离缝

图8为支承层最大拉应力的变化情况。下部边界为路基面时，LS越小，支承层承受的拉应力越大，当LS在60 m及以内时，支承层的最大拉应力基本超过了设计强度。下部边界为地基面时，当LF在10 m及以内时，支承层的拉应力较大；而当LF超过40 m以后，支承层的最大拉应力很小。

图8　支承层承受的最大拉应力

对计算结果的分析表明，下部边界为路基面时，路基变形引起的轨道不平顺可以处在中短波范围内，这与已经形成的基本共识不符；由于双块式无砟轨道的稳定一般取决于道床板与支承层间的摩阻力，当道床板与支承层之间出现大的离缝时，将会影响无砟轨道结构的稳定性；支承层如果产生很大的拉应力，而且远远超过其水硬性材料或C15素混凝土的设计强度，无砟轨道结构将出现严重伤损。双块式无砟轨道作为自上而下刚度逐渐递减的连续结构，其支承层不是无砟轨道主要承受荷载的结构层，如果层间离缝威胁到无限位连续结构的稳定性，这在设计上是不允许的，也不是该无砟轨道结构应当具有的实际状况。因此，由下部边界为路基面的计算模型所得到的计算结果与双块式无砟轨道的设计原理和现场实际不符。

2.2　层间关系的对比分析

应用下部边界为地基面的计算模型，对道床板与支承层按层间接触和层间结合良好2种层间关系进行对比分析，其中按层间接触的计算结果如图3、图4、图7(b)、图8(b)所示。

当道床板与支承层结合良好时，其路基和轨道的变形情况如图9所示，地基面上的变形向上传递的规律与图3相似，差别是在地基面变形的波长为10 m时，由于轨道板与支承层良好结合后它们的抗弯刚度增大，从而在支承层与路基面间产生了离缝。

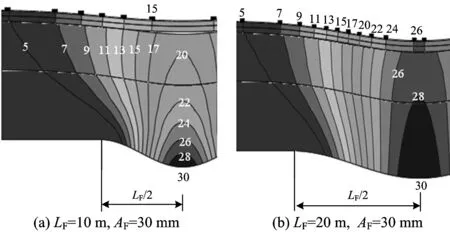
图9　层间结合时路基和轨道的变形等值线图

道床板与支承层按层间结合良好时，波长和幅值传递比的计算结果如图10所示。由图10可知，波长传递比随LF和AF的变化规律与图4(a)所示相一致，但其量值要小于道床板与支承层按层间接触的情况；幅值传递比在LF不超过30 m时随AF的增大而减小，且小于图4(b)所示的道床板与支承层按层间接触计算得到的量值。

图10道床板与支承层结合良好时波长和幅值的传递比计算结果

由计算分析的结果表明，这2种层间关系对波长和幅值传递比影响的差异主要体现在LF为30 m以内时幅值传递比的不同，其主要原因如图11所示，当道床板与支承层按层间结合良好考虑时，2层结构形成了1层“复合板”，抗弯刚度增大，跟随路基变形的性能变差，当AF增大时，“复合板”与路基面之间的离缝也增大；而道床板与支承层按层间接触处理时，支承层的弹性模量和层厚均较“复合板”小，抗弯能力差，其与路基面之间的离缝可忽略不计。

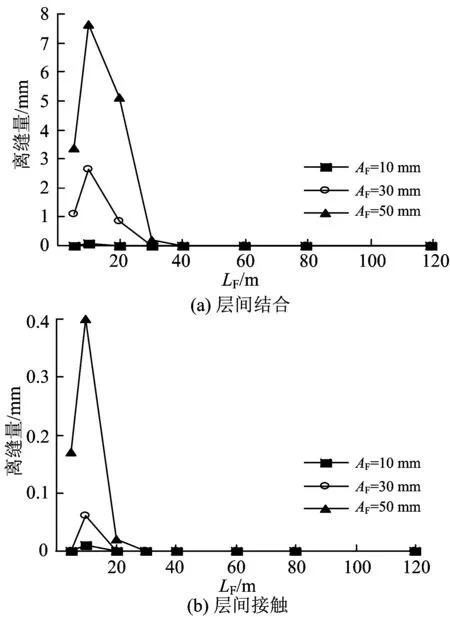
图11　支承层与路基面间的离缝

在道床板与支承层间结合良好的层间关系下，若支承层与路基面间在路基变形波长较小时产生较大离缝，则支承层所承受的拉应力随之增大，如图12所示，与图8(b)相比，支承层所承受的最大拉应力大于道床板与支承层按层间接触处理的层间关系下的值，且容易超过材料的设计强度。

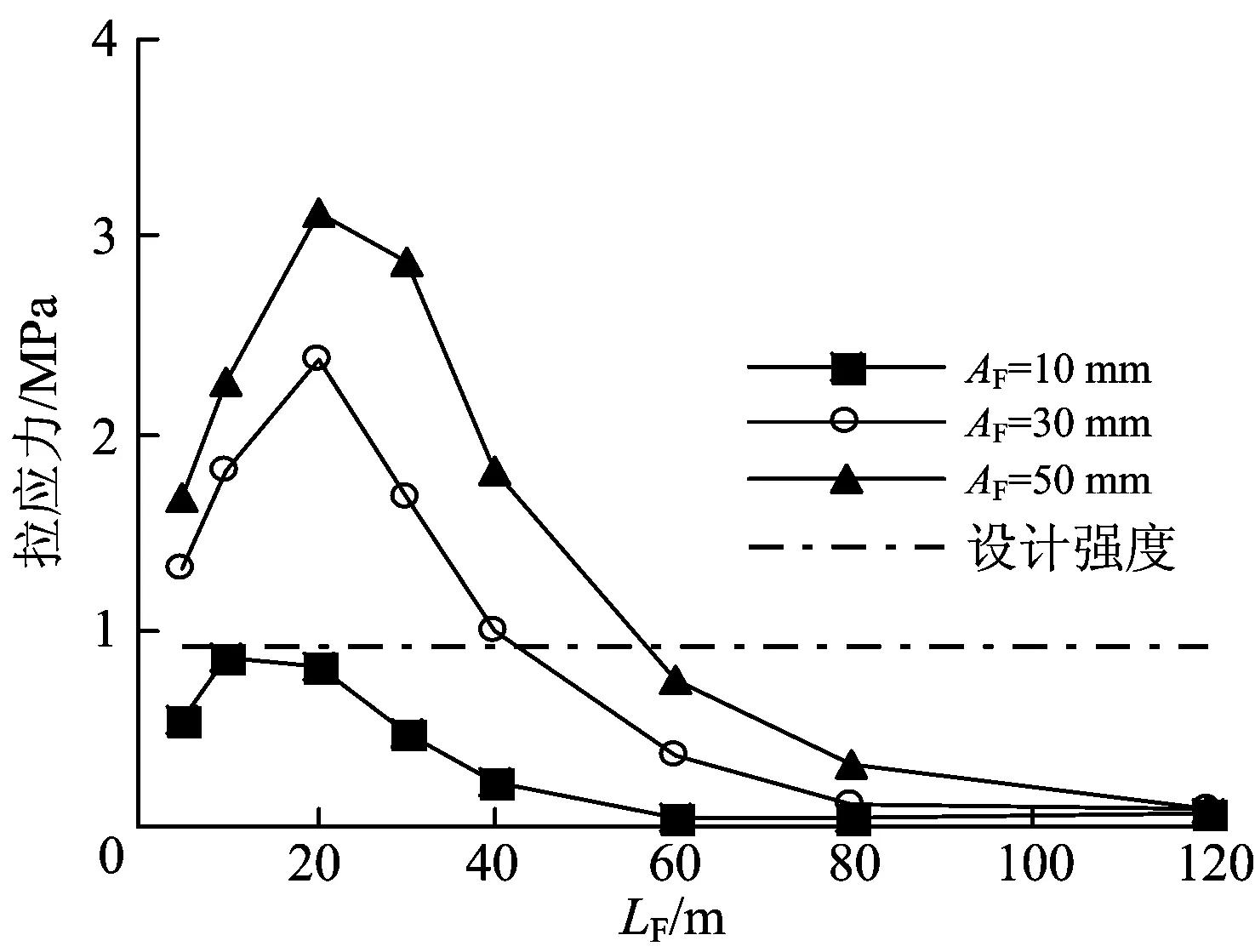
图12　支承层承受的最大拉应力

通过对计算结果的分析可以看出，对层间关系的处理影响着无砟轨道结构的受力和变形，特别是按层间结合良好考虑层间关系的条件下，支承层与路基面间的离缝以及支承层承受较大的拉应力，均与前述下部边界为路基面时的计算结果相似，这不符合该无砟轨道结构应当具有的状况和设计原理。

3　结　论

作者提出了构建无砟轨道—路基变形计算模型的原则，首次提出模型的下部边界条件应基于路基工后沉降的机理确定，无砟轨道结构的层间关系应基于路基变形对轨道不平顺、结构稳定性和伤损的影响来确定。

通过建立的双块式无砟轨道—路基变形计算模型，分析不同边界条件和层间关系的计算结果表明，当计算模型的下部边界为地基面时，由于路基本体在变形传递过程中产生的变形扩散作用，从而引起轨道变形的增大呈漏斗状传递形式，并且产生的轨道不平顺一般为长波不平顺，这符合轨道长波不平顺的产生机理；当计算模型的下部边界为路基面时，由于输入的路基变形对无砟轨道的“强制性”作用，从而改变了无砟轨道与路基变形之间的相互作用关系，导致道床板与支承层间的离缝过大，支承层出现的拉应力远远超过结构的设计强度，这不符合双块式无砟轨道的结构原理及应具有的实际状况，由此验证了无砟轨道—路基变形计算模型的下部边界选择地基面的原则是合理、可靠的。按道床板与支承层结合良好来处理层间关系时，由于道床板与支承层共同形成复合结构层，从而增大了结构层的抗弯刚度，使得在路基变形荷载的作用下，该复合结构层与路基面之间出现了离缝，改变了路基变形对轨道不平顺的影响规律；另外在支承层上也产生了较大的拉应力，成为无砟轨道结构承受荷载的主要结构层，这与双块式无砟轨道的结构原理不符，从而验证了无砟轨道—路基变形计算模型中将结构层间处理成接触关系更为符合实际。

以下部边界为地基面和将层间关系按接触关系处理所构建的无砟轨道—路基变形计算模型，能够计算分析路基变形对轨道不平顺、无砟轨道结构稳定性及无砟轨道结构和路基受力、伤损的影响规律，这种影响规律可用来指导不同路基参数下、不同无砟轨道结构形式下路基变形管理标准的制定和分析，以及无砟轨道的结构设计和养护维修。

[1]赵国堂. 高速铁路无砟轨道结构[M]. 北京：中国铁道出版社，2006.

[2]LUTZ Vogt, ERICH Rehfeld. Behaviour of Slab Track under Extreme Stress Conditions[R]. Bruxelles：Baugrund Dresden，2005.

[3]中华人民共和国交通部国家铁路局.TB 10621—2014 高速铁路设计规范[S].北京：中国铁道出版社， 2015.

[4]韩义涛，姚力. 基础沉降对土路基上板式轨道动力性能影响分析[J]. 铁道工程学报，2007(10)：28-31.

(HAN Yitao，YAO Li. Analysis of the Dynamic Performance for Slab Track Settlement on Embankment [J]. Journal of Railway Engineering Society，2007(10)：28-31.in Chinese)

[5]王森荣，赵坪锐，孙立. 无砟轨道基础变形影响计算方法的研究[J]. 铁道标准设计，2008(4)：72-74.

(WANG Senrong，ZHAO Pingrui，SUN Li. Study on Calculation Method for Influence of Foundation Deformation of Ballastless Track [J]. Railway Standard Design, 2008(4)：72-74. in Chinese)

[6]陈鹏，高亮，马鸣楠. 高速铁路路基沉降限值及其对无砟轨道受力的影响[J]. 工程建设与设计，2008(5)：63-66.

(CHEN Peng，GAO Liang，MA Mingnan. Limited Value of Subgrade Settlement and Its Influence on Mechanical Characteristics of Ballastless Track in High-Speed Railway [J]. Construction & Design for Project，2008(5)：63-66. in Chinese)

[7]刘茹冰，张士杰. 路基沉降不均对板式轨道受力的影响分析[J]. 路基工程，2009(1)：142-143.

(LIU Rubing，ZHANG Shijie. Influence of Uneven Subgrade Settlement on Stress of Slab Track [J]. Subgrade Engineering，2009(1)：142-143. in Chinese)

[8]高增增. 路基不均匀沉降对双块式无砟轨道结构受力影响分析[J]. 中国铁路，2010(7)：74-76.

(GAO Zengzeng. Influence of Non-Uniform Subgrade Settlement on Stress of Double-Block Ballastless Track [J]. China Railways，2010(7)：74-76. in Chinese)

[9]周萌，宫全美，王炳龙，等. 路基不均匀沉降值对板式轨道动力响应的影响[J].铁道标准设计，2010(10)：1-4.

(ZHOU Meng，GONG Quanmei，WANG Binglong，et al. Influence of Uneven Sedimentation Value of Subgrade on Dynamic Response of Slab Tracks [J]. Railway Standard Design，2010(10)：1-4. in Chinese)

[10]徐庆元，李斌，范浩. 路基不均匀沉降对列车—路基上无砟轨道耦合系统动力特性的影响[J]. 铁道科学与工程学报，2012，9(3)：13-19.

(XU Qingyuan，LI Bin，FAN Hao. Influence of Uneven Settlement of Subgrade on Dynamic Characteristic of Train-Ballastless Track on Subgrade Coupling System [J]. Journal of Railway Science and Engineering，2012，9(3)：13-19. in Chinese)

[11]徐庆元，李斌，周智辉. CRTS-Ⅰ型板式无砟轨道线路路基不均匀沉降限值研究[J].中国铁道科学，2012，33(2)：1-6.

(XU Qingyuan，LI Bin，ZHOU Zhihui. Study on the Limited Value for the Uneven Settlement of Subgrade under CRTS-Ⅰ Type Slab Track [J]. China Railway Science，2012，33(2)： 1-6. in Chinese)

[12]徐庆元，范浩，李斌，等.CRTS-Ⅱ型板式无砟轨道线路路基不均匀沉降限值研究[J]. 中南大学学报：自然科学版，2013，44(12)：5038-5044.

(XU Qingyuan，FAN Hao，LI Bin，et al. Limited Value for Uneven Settlement of Subgrade under CRTS-Ⅱ Type Slab Track [J]. Journal of Central South University：Science and Technology，2013，44(12)：5038-5044. in Chinese)

[13]王启云，张家生，孟飞. 不均匀沉降对无砟轨道路基动力特性的影响[J]. 铁道标准设计，2014，58(10)：17-21.

(WANG Qiyun，ZHANG Jiasheng，MENG Fei. The Influence of Settlement on Dynamic Characteristics of Ballastless Track Subgrade [J]. Railway Standard Design，2014，58(10)：17-21. in Chinese)

[14]高亮，赵磊，曲村，等. 路基上CRTS Ⅲ型板式无砟轨道设计方案比较分析[J]. 同济大学学报：自然科学版，2013，41(6)：848-855.

(GAO Liang，ZHAO Lei，QU Cun，et al. Analysis on Design Scheme of CRTS Ⅲ Slab Track Structure on Roadbed [J]. Journal of Tongji University：Natural Science，2013，41(6)：848-855. in Chinese)

[15]赵立宁，蔡小培，曲村. 地面沉降对路基上单元板式无砟轨道平顺性的影响分析[J]. 铁道标准设计，2013(10)：15-18.

(ZHAO Lining，CAI Xiaopei，QU Cun. Influence of Land Subsidence on the Regularity of the Ballastless Track with Unit Slabs[J]. Railway Standard Design，2013(10)：15-18. in Chinese)

[16]蔡小培，刘 薇，王璞，等. 地面沉降对路基上双块式无砟轨道平顺性的影响[J]. 工程力学，2014，31(9)：160-165.

(CAI Xiaopei，LIU Wei，WANG Pu，et al. Effect of Land Subsidence on Regularity of Double-Block Ballastless Track [J]. Engineering Mechanics，2014，31(9)：160-165. in Chinese)

[17]张小会，周顺华，宫全美，等. 路基不均匀沉降对车辆和轨道动力响应的影响[J]. 同济大学学报：自然科学版，2015，43(8)：1187-1253.

(ZHANG Xiaohui，ZHOU Shunhua，GONG Quanmei，et al. Effect of Subgrade Differential Settlement on Dynamic Response of Vehicle and Slab Track Vertical Coupled System [J]. Journal of Tongji University： Natural Science，2015，43(8)：1187-1253. in Chinese)

[18]肖威，郭宇，高建敏，等. 高速铁路路基不均匀沉降对CRTSⅢ板式轨道受力变形的影响[J]. 铁道科学与工程学报，2015，12(4)：724-730.

(XIAO Wei，GUO Yu，GAO Jianmin，et al. Effect of Uneven Subgrade Settlement on the CRTS Ⅲ Slab Track Stress and Deformation of High-Speed Railway [J]. Journal of Railway Science and Engineering，2015,12(4)：724-730. in Chinese)

[19]中华人民共和国铁道部. TB10601—2009 高速铁路工程测量规范[S]. 北京：中国铁道出版社，2010.