基于随机介质理论的软土路基注浆位移计算方法
2016-04-10杨新安
郭 乐,杨新安,罗 驰,邱 龑,王 薇
(同济大学 道路与交通工程教育部重点实验室,上海 201804)
建于软土之上的铁路建成通车后,受施工工艺和质量、地质环境变化以及车辆长期循环荷载作用等因素的综合影响,路基会出现不均匀沉降。由于软土的低强度、高含水率、高压缩性等特点,软土路基的沉降现象更为普遍,出现沉降病害后给行车安全带来巨大隐患。软土路基沉降治理的方法有限,郭乐等[1]对注浆法治理软土路基沉降进行了现场试验,说明了注浆是治理软土路基沉降的合理可行方法,且研究了注浆施工对土体扰动的规律。但要想达到理想的沉降治理效果,需严格控制注浆对土体的扰动,因此有必要对注浆引起的土体位移进行研究。
相对于软土排水固结所需时间而言,软土注浆施工时间较短,可视为不排水过程,同时浆液无法渗入软土孔隙中,注入的浆泡依靠挤土作用迫使土体表面向上隆起获得空间补偿。目前用于注浆引起软土位移的计算方法主要有数值模拟[2-5]、小孔扩张理论[6-8]和随机介质理论[9-10]。注浆治理沉降的核心问题是挤土作用引起土体位移,土中应力变化是次要的,而数值模拟方法和小孔扩张理论均基于传统岩土弹塑性理论求得的土体应力场求解位移场。由于软土渗透性差,水泥浆无法渗入土体,因此注浆前后的浆泡体积膨胀量是明确的,可用随机介质理论描述这一膨胀过程,将土体视为随机介质,用随机方法直接求解土体位移。
李立新等[9]基于随机介质理论,将浆泡扩张视为均匀扩张过程,分别推导出单个浆泡和多个浆泡共同作用引起地表位移的计算式,并与数值模拟结果和现场实测结果进行比较分析。但浆泡均匀扩张为理想情况,实际上应考虑为非均匀扩张。章敏等[10]同样基于随机介质理论,将浆泡扩张视为均匀扩张和非均匀2种模式,推导出注浆引起地表位移的计算式,并计算双浆泡扩张的共同影响,但这种非均匀扩张视浆泡底部位移为零,实际上浆泡底部也应有向下扩张的位移,浆泡的总体扩张呈现浆泡顶部位移大于底部位移的非均匀扩张。
本文基于随机介质理论,视浆泡顶部与底部扩张位移不相等的非均匀球扩张过程,建立土体位移计算方法,并将该方法的计算结果与现场试验结果进行比较分析,说明该方法的可行性。
1 单孔注浆土体位移
1.1 土体位移场基本方程
根据随机概念[11-12],把浆泡扩张看作一定范围内的众多个无限小单元的膨胀,总的扩张结果应等于各个单元膨胀引起结果的总和。设在土体中(ξ,ζ,η)处有一边长分别为dξ,dζ,dη的单元发生膨胀,如图1所示其在(x,y,z)处引起的竖向位移uez、水平位移uex和uey为
(1)
式中:xe,ye和ze分别为(x,y,z)处沿X,Y和Z方向的变形量;r1(ze)和r2(ze)分别为单元发生膨胀在地层走向方向和倾斜方向上的影响范围;ρ(ze)为膨胀形态向地层倾斜方向的偏移量。
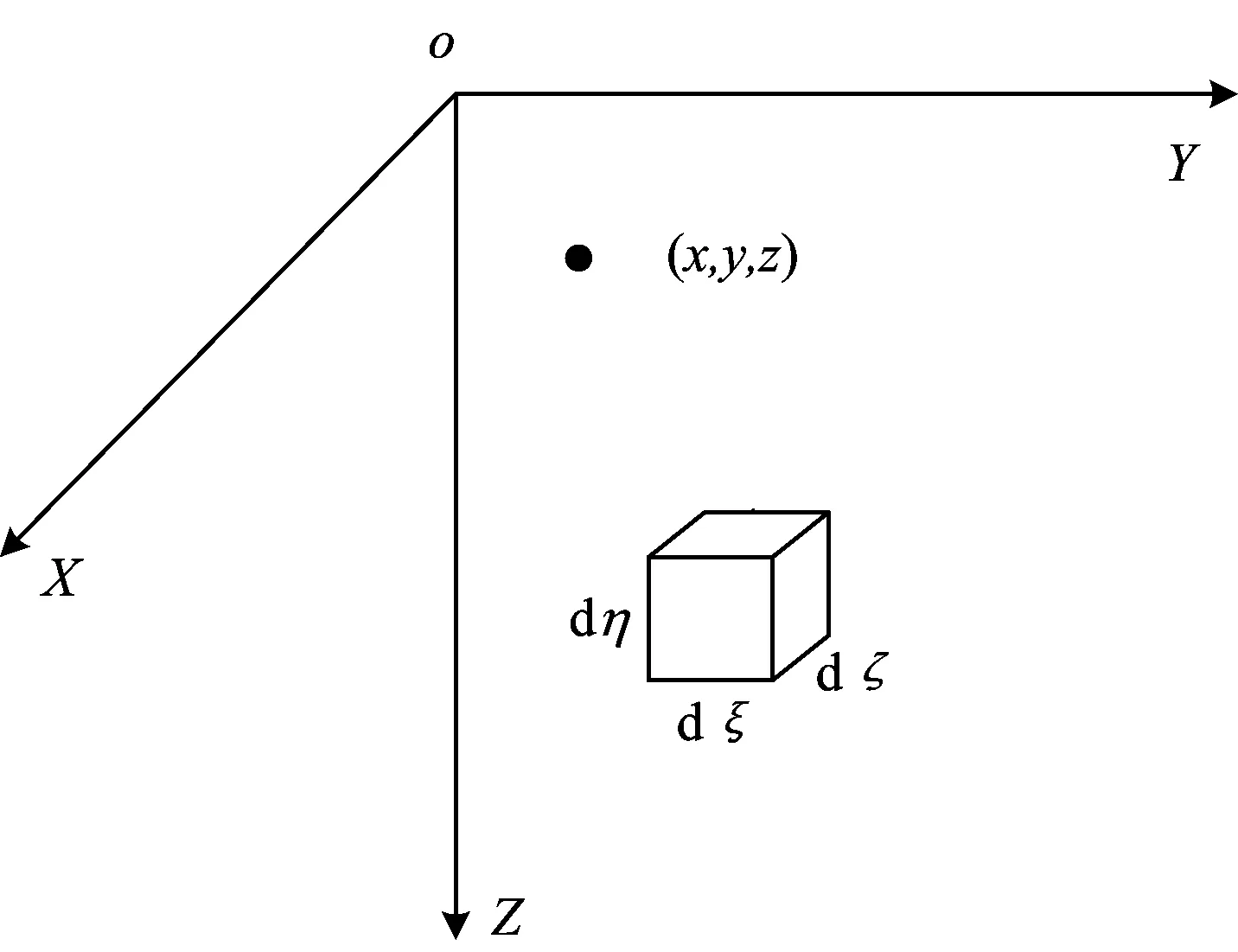
图1 浆泡单元体膨胀示意图
当土体呈水平成层分布时,r1(ze)=r2(ze)=r(ze),ρ(ze)=0, 且r(ze)=(z-η)/tanβ(β为地层影响范围角,取决于开挖地层的性质),则式(1)可写为
(2)
故浆泡由体积ω膨胀为体积Ω后引起土体内任意一点(x,y,z)产生的位移为
(3)
式中:a1,b1,c1,d1,e1,f1为浆泡膨胀前的区域积分限;a2,b2,c2,d2,e2,f2为浆泡膨胀后的区域积分限,各积分限的确定由浆泡扩张模式确定。
1.2 浆泡非均匀扩张模式修正
随着水泥浆注入土体过程中浆泡的扩张,浆泡下部受到的土体抵抗作用大于浆泡顶部,导致浆液底部的土体位移发生偏转,如图2(a)所示,使得水泥浆更易向上扩张,从而形成浆泡中心点高于注浆点,因此要对浆泡非均匀扩张模式进行修正。
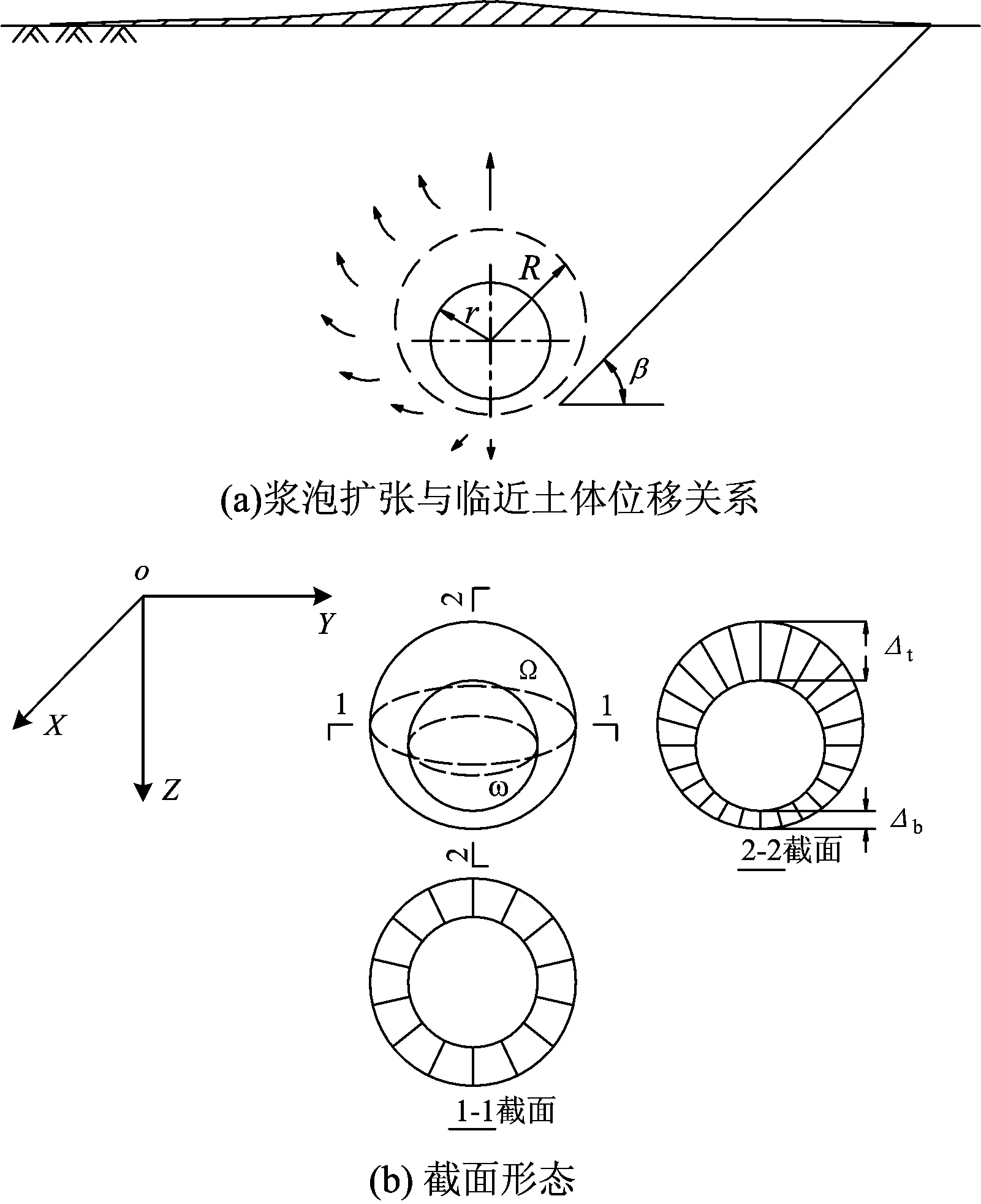
图2 浆泡的非均匀扩张形态
假定:注浆前后浆泡的形状均呈球形,浆泡呈非均匀扩张,即在任一水平截面上浆泡呈均匀扩张,而在任一垂直截面上浆泡呈非均匀扩张,且浆泡顶点和底点分别为扩张位移的最大和最小点,如图2(b)所示;注浆点位于地表原点位置的正下方且距地面的距离为H,注浆前和注浆后浆泡半径分别为r和R,r取注浆管半径,浆泡上部顶点的扩张位移量为Δt,下部底点的扩张位移量为Δb,则有
(4)
(5)
实际注入土中的浆泡体积Ve与注浆量Vinj并非完全相等,用注浆效率δ表示,即
(6)
AU等人[13]通过室内实验证明注浆效率受注浆时间和超固结比的影响,随着注浆时间的增加和超固结比的减小,注浆效率呈下降趋势,水泥浆液的压缩模量和高压脱水性也是另一重要影响因素。
1.3 浆泡非均匀扩张参数反分析
强化食品安全管理。建立健全的食品安全管理组织,配置食品安全管理人员;建立、落实各项卫生制度;对从业人员进行全员食品安全培训,树立食品安全意识;定期开展食品安全自查,发现问题及时改正;强化自身卫生管理,落实岗位责任;争取条件,开展瘦肉精、农残等食品安全快速检验。
(7)
约束条件为
Δt>Δb
(8)
采用不可行度退火算法处理约束条件,应用遗传算法进行最优解的搜索。任意解xm的不可行度φ(xm)定义为解xm到可行域的距离,即
φ(xm)=[min{0,Δt-Δb}]2
(9)
xm与可行域的距离越远则不可行度越大,反之就越小;当xm为可行解时,不可行度为0。利用不可行度函数φ(xm),采用模拟退火算法,对解xm的不可行度进行优化调整[16],使其逐步逼近可行解。为满足遗传算法对适应度函数最大的要求,实际求解时将目标函数的最小化问题转化为最大化问题,构造适应度函数
(10)
2 多孔注浆土体位移场
2.1 多孔注浆土体位移场
相邻注浆孔的位置关系及其相互影响可分为图3所示的3种情况,图中A和B表示注浆孔单独影响区域,C表示相邻注浆孔共同影响区域。当注浆孔紧邻时,如图3(a)所示,由于相邻注浆孔之间相互干扰,使得共同影响区域C的范围过大。这种注浆孔布置对土体扰动过大,注浆影响范围过小,注浆效果不理想。当注浆孔相距较远时,如图3(c)所示,注浆对土体产生的位移不存在共同影响区域C,故可按单孔注浆情况进行计算。当注浆孔相距一定距离但又存在共同影响区域C时,如图3(b)所示,则需按照多孔注浆位移计算方法进行计算。
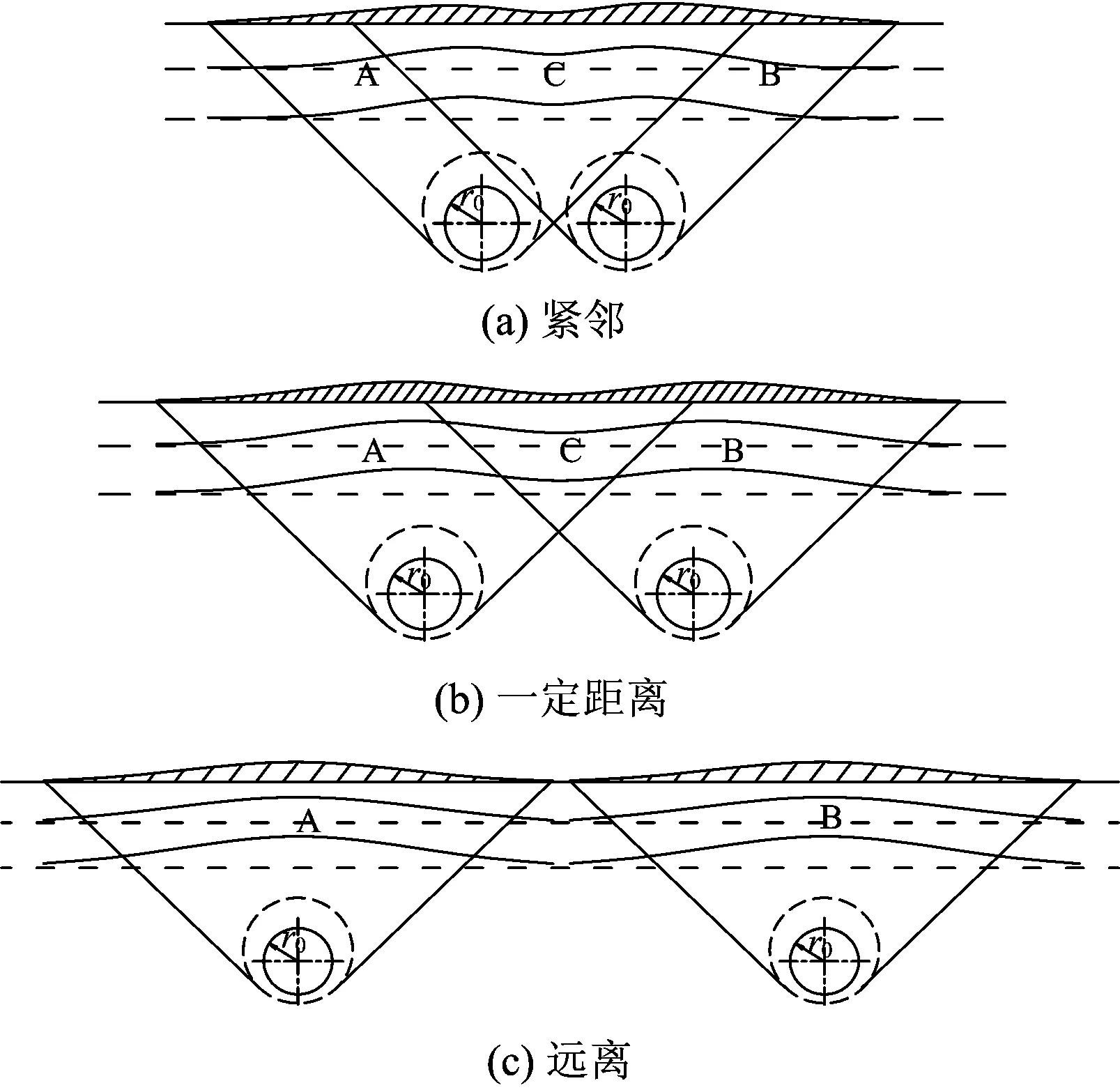
图3 相邻注浆孔位置关系及影响情况
相邻注浆孔共同影响区域内土体的位移叠加效应可以采用随机介质理论结合叠加原理进行计算[17]。设由k个注浆孔进行注浆,uzl,uxl和uyl(l=1,…,k)分别为注浆孔的竖向位移、X向水平位移和Y向水平位移,各注浆孔全部进行注浆后土体中任意一点产生的位移为
(11)
2.2 多浆泡非均匀扩张模式修正
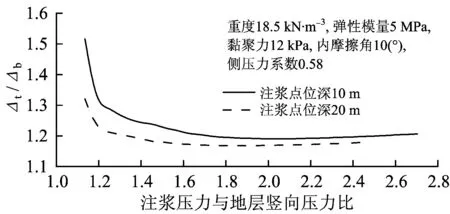
图4 浆泡顶部与底部位移比变化趋势
对γ进行反分析求解时,式(5)中Δt应改写为γΔb,同时为方便积分,可依据每个注浆点中心位置单独设置坐标系,则多孔注浆时单个浆泡扩张后的各积分限为
(12)
则约束条件式(8)也应改写为
γ>1
(13)
2.3 浆泡扩张模式参数的反分析求解
根据式(7)和式(11)建立求解多孔注浆扩张模式参数反分析的目标函数
(14)
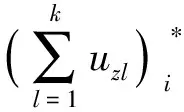
根据已建立的目标函数式(14),基于模拟退火遗传算法原理及浆泡扩张引起地表位移的计算式(3)和式(11),以地表变形的现场实测数据为反分析输入量,编制反分析程序进行求解,获得多孔注浆扩张模式参数。
3 现场试验验证
为验证本文方法的可靠性,开展某运营铁路路基注浆的现场试验,并将地表变形实测值与采用本文方法的计算值进行对比分析。该运营铁路沿线软土分布广泛,第四系堆积层广泛发育,路基不均匀沉降显著,通车后沉降仍未趋于稳定,部分路段最大不均匀沉降量超过工后沉降的控制标准,因此采用注浆方法对路基进行抬升,注浆管布置如图5所示。注浆材料采用单液水泥浆,地表10 m以下地层注浆压力为0.5 MPa,注浆速度为1~2 m3·h-1,结合该段线路的地质条件(表1),实际注浆过程中以注浆量为主要控制指标。
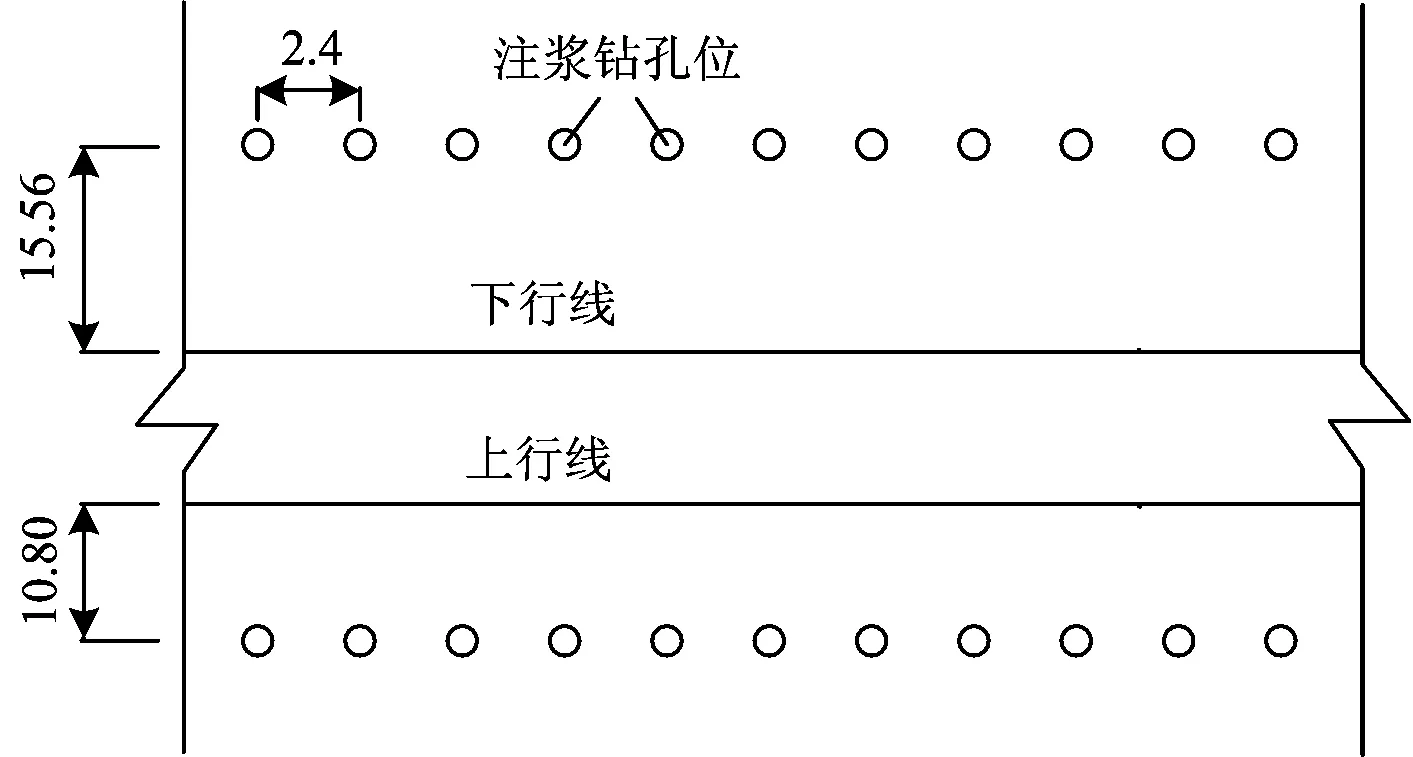
图5 注浆管布置图(单位:m)
图6给出了8月12日注浆施工引起地表变形的实测值,图中竖线表示注浆位置,注浆深度为30 m,位于淤泥质黏土层内。每孔注浆量为7~9 m3,根据室内试验和现场试验综合判断,注浆效率取60%,通过反分析求得浆泡扩张参数γ=1.5,tanβ=0.5。

表1 主要土层物理力学性质
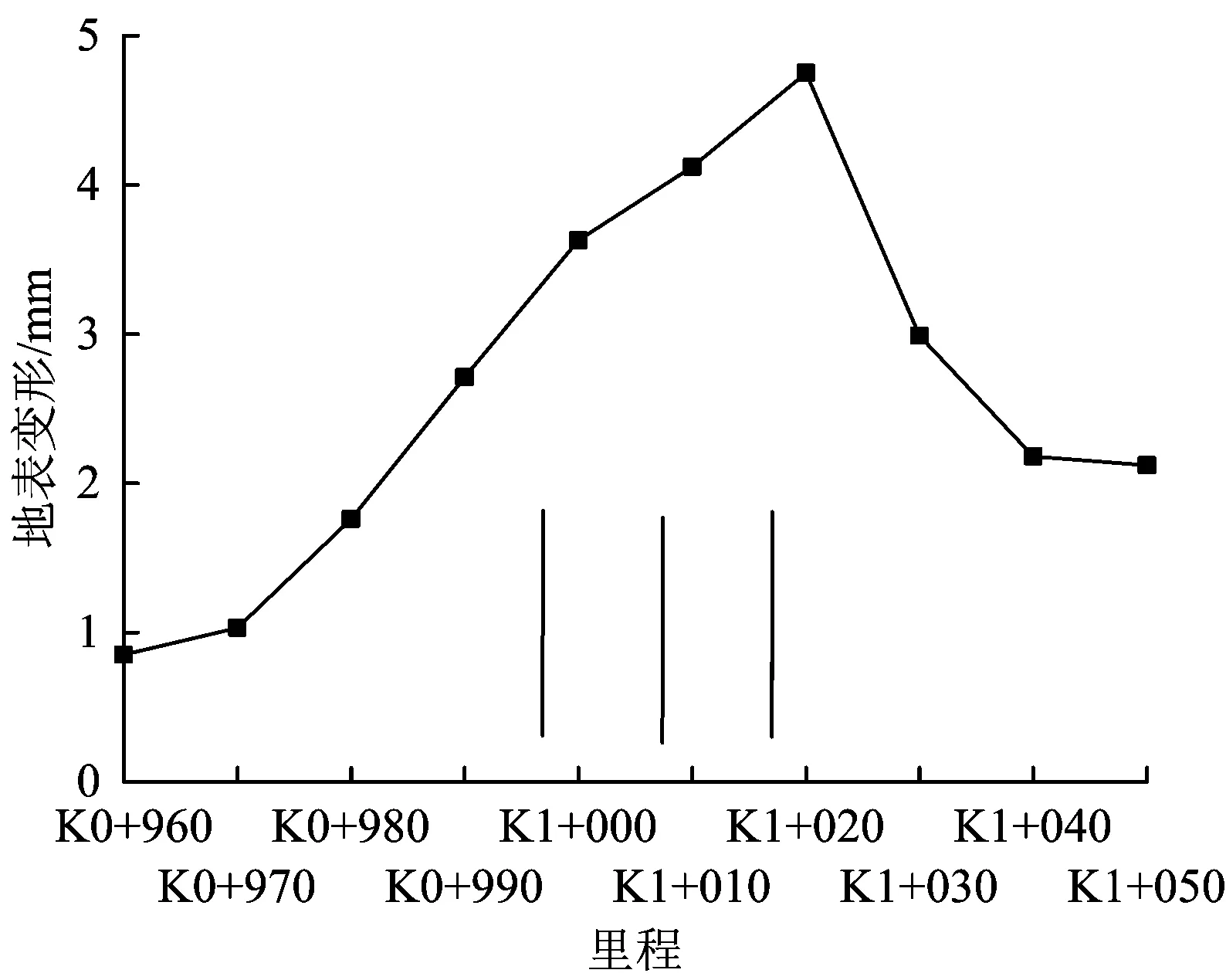
图6 多孔注浆引起地表竖向变形的实测值
图7给出8月14日和8月15日多孔注浆引起的地表竖向变形实测值及利用反分析方法求得的计算值,注浆深度为30 m,图中竖实线位置8月14日和15日均进行了注浆,竖虚线位置为8月15日进行了注浆,对比地表竖向变形计算值与实测值发现,两者差值在0.3~1.6 mm,距离注浆孔20 m范围内的误差在20%以内,距离注浆孔较远处的误差较大。
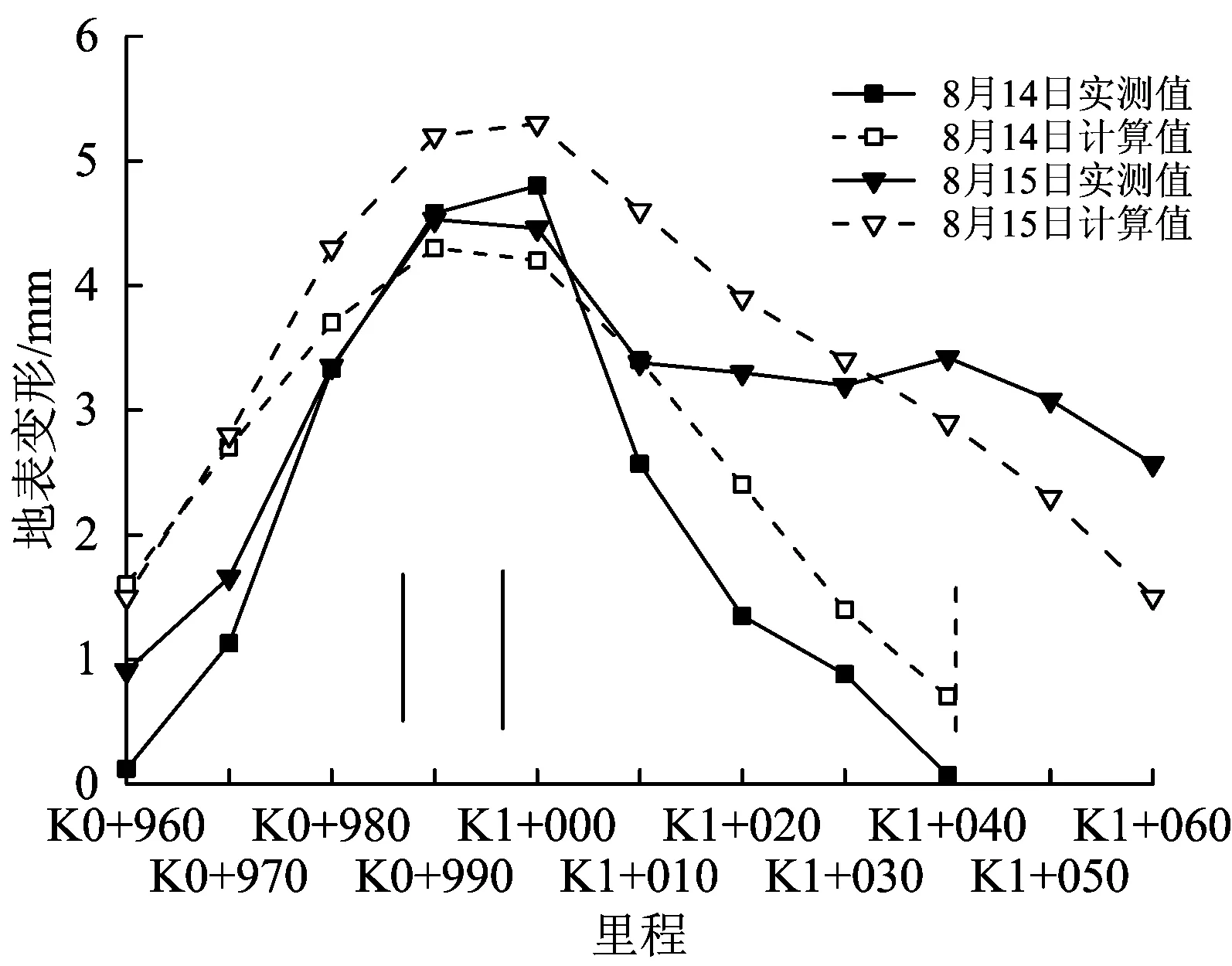
图7 地表竖向变形的实测值与计算值
图8为8月15日注浆后线路一侧地表以下土体沿线路纵向的水平位移计算值与里程K1+1 010处的实测值。由图8可见,在地表9 m以下深度的计算值与实测值吻合度较好;9 m以上土体的水平位移实测值发散是由于测斜仪自身工作原理和测斜管刚度导致,不能反映真实土体的水平位移。里程K1+1 010和K1+1 030分别靠近2个不同注浆点位,其水平位移计算值方向相反,但绝对值均大于里程K1+1 020处,这与实际规律一致。由于考虑了浆泡的非均匀扩张和地层影响范围角β,使得水平位移计算值的最大值所处深度要稍大于注浆点位,离注浆点越远处的断面水平位移最大值所在深度也随之上移。
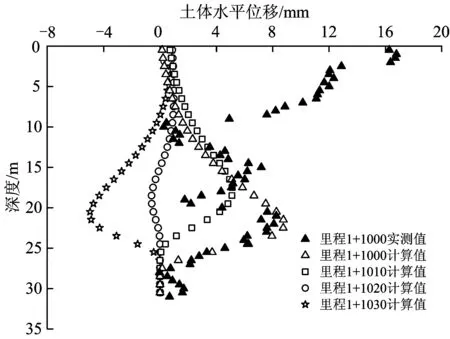
图8 地表以下土体水平位移实测值与计算值
地表竖向变形、地表以下土体水平位移的计算值和实测值对比结果表明,利用本文方法可对注浆引起的土体位移进行预测。如注浆点数与土体变形的实测数据增多,进行反分析的输入数据也会增多,则可以提高浆泡扩张模式参数的反分析精度,所得结果也将更符合实际情况。
4 结 语
本文提出浆泡的非均匀扩张模式,认为浆泡扩张时其顶部和底部的土体都会发生扩张位移,且顶部位移大于底部位移,并基于随机介质理论,建立了单孔注浆时浆泡非均匀扩张引起土体位移的计算式,并提出采用模拟退火遗传算法结合现场实测的方法对非均匀扩张模式的参数进行反分析求解。当计算多孔注浆的情况时,不同注浆孔的非均匀扩张特征可用浆泡顶部与底部位移的比值表征,相邻注浆孔共同影响区域内土体的位移可基于叠加原理并结合单孔注浆位移计算式进行求解。长三角某运营铁路路基的现场试验实测值和计算值的对比分析表明,在地表以下30 m深度处注浆,地表竖向变形实测值和计算值的差值在0.3~1.6 mm范围内,距离注浆孔20 m范围内的误差在20%以内,离注浆孔水平位置越远误差较大,地表以下土体水平位移计算值的变化规律与实际规律一致,说明利用本文方法可对注浆引起的土体位移进行计算。
[1]郭乐, 杨新安, 吴东鹏, 等. 高速铁路软土复合路基沉降注浆治理现场试验研究[J]. 中国铁道科学, 2015,36(6):1-7.
(GUO Le, YANG Xinan, WU Dongpeng, et al. Field Test on Treating Settlement by Grouting for Soft Soil Composite Subgrade of High Speed Railway[J]. China Railway Science, 2015,36(6):1-7. in Chinese)
[2]唐智伟, 赵成刚. 注浆抬升地层的机制、解析解及数值模拟分析[J]. 岩土力学, 2008,29(6):1512-1516.
(TANG Zhiwei,ZHAO Chenggang. Mechanisms of Ground Heave by Grouting and Analytical Solutions & Numerical Modeling[J]. Rock and Soil Mechanics, 2008,29(6):1512-1516. in Chinese)
[3]张志沛, 彭惠, 饶晓. 软土地基注浆扩散过程数值模拟研究[J]. 岩土力学, 2011,32(增1):652-655.
(ZHANG Zhipei, PENG Hui, RAO Xiao. Numerical Simulation Study of Grouting Diffusion Process in Soft Soil Foundation[J]. Rock and Soil Mechanics, 2011,32(Supplement 1):652-655. in Chinese)
[4]WANG S Y, CHAN D H, LAM K C, et al. Numerical and Experimental Studies of Pressure-Controlled Cavity Expansion in Completely Decomposed Granite Soils of Hong Kong[J]. Computers and Geotechnics, 2010,37(7):977-990.
[5]AU S, SOGA K, JAFARI M R, et al. Factors Affecting Long-Term Efficiency of Compensation Grouting in Clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003,129(3):254-262.
[6]EL-KELESH M, MOSSAAD M E, BASHA I M. Model of Compaction Grouting[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001,127:955-964.
[7]邹金锋, 李亮, 杨小礼, 等. 劈裂注浆能耗分析[J]. 中国铁道科学, 2006,27(2):52-55.
(ZOU Jinfeng, LI Liang, YANG Xiaoli, et al. Energy Dissipation Analysis for Crack Grouting[J]. China Railway Science, 2006,27(2):52-55. in Chinese)
[8]邹健, 张忠苗. 考虑压滤效应饱和黏土压密注浆球孔扩张理论[J]. 哈尔滨工业大学学报, 2011,43(12):119-123.
(ZOU Jian, ZHANG Zhongmiao. Spherical Cavity Expansion Theory of Compaction Grouting in Saturated Clay Considering Pressure Filtration[J]. Journal of Harbin Institute of Technology, 2011,43(12):119-123. in Chinese)
[9]李立新, 童无欺, 邹金锋. 注浆抬升位移的随机介质理论预测方法[J]. 铁道科学与工程学报, 2013,10(5):47-51.
(LI Lixin, TONG Wuqi, ZOU Jinfeng. Study on Grouting Uplift Displacement Prediction Using Stochastic Medium Theory[J]. Journal of Railway Science and Engineering, 2013,10(5):47-51. in Chinese)
[10]ZHANG M, WANG X, WANG Y. Mechanism of Grout Bulb Expansion and Its Effect on Ground Uplifting[J]. Journal of Central South University of Technology, 2011,18(3):874-880.
[11]刘宝琛. 随机介质理论及其在开挖引起的地表下沉问题中的应用[J]. 中国有色金属学报, 1992,2(3):8-14.
(LIU Baochen. Stochastic Medium Theory and Its Application in Ground Subsidence Caused by Excavation[J]. The Chinese Journal of Nonferrous Metals, 1992,2(3):8-14. in Chinese)
[12]乔世范. 随机介质变形破坏判据研究及其工程应用[D]. 长沙: 中南大学, 2006: 38-61.
(QIAO Shifan. Study on the Deformation Failure Criterion Stochastic Medium and Its Application[D]. Changsha: Central South University, 2006: 38-61. in Chinese)
[13]SOGA K, AU S, JAFARI M R, et al. Laboratory Investigation of Multiple Grout Injections into Clay[J]. Geotechnique, 2004,54(2):81-90.
[14]朱文彬, 张家生, 刘宝琛. 随机介质理论在深基坑稳定性分析中的应用[J]. 岩土力学, 1998,19(2):14-18.
(ZHU Wenbin, ZHANG Jiasheng, LIU Baochen. Application of Stochastic Medium Theory to Investigation of Stability of Foundation Pit[J]. Rock and Soil Mechanics, 1998,19(2):14-18. in Chinese)
[15]张家生, 刘宝琛. 随机介质理论基本参数的反分析确定[J]. 湘潭矿业学院学报, 2004,19(1):5-8.
(ZHANG Jiasheng, LIU Baochen. Determination of Basic Parameters in Stochastic Method by Back Analysis[J]. Journal of Xiangtan Mining Institute, 2004,19(1):5-8. in Chinese)
[16]王新坤. 基于模拟退火遗传算法的自压树状管网优化[J]. 水利学报, 2008,39(8):1012-1016.
(WANG Xinkun. Optimization of Gravity Pipe Network Based on Annealing Genetic Algorithm[J].Journal of Hydraulic Engineering, 2008,39(8):1012-1016. in Chinese)
[17]阳军生, 刘宝琛. 城市隧道施工引起的地表移动及变形[M].北京: 中国铁道出版社, 2002: 19-31.
(YANG Junsheng, LIU Baochen. Ground Movement and Deformation Induced by Urban Tunnel Construction[M]. Beijing: China Railway Publishing House, 2002: 19-31. in Chinese)
