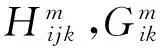双材料V型切口应力强度因子的加料有限元分析*

杨军辉，韩珺礼，雷勇军，蒙上阳

(1．国防科技大学 航天科学与工程学院， 湖南 长沙　410073； 2．北京特种机电技术研究所， 北京　100012)



双材料V型切口应力强度因子的加料有限元分析*

杨军辉1,2，韩珺礼2，雷勇军1，蒙上阳2

(1．国防科技大学 航天科学与工程学院， 湖南 长沙410073； 2．北京特种机电技术研究所， 北京100012)

摘要：应用Williams本征函数展开和线性变换求解V型切口端部渐进位移场。将该位移场加入常规等参单元位移模式中，构造双材料V型切口加料单元和过渡单元的位移模式，推导加料有限元方程。建立带V型缺口双材料三点弯曲梁试件和直角界面端平面问题的加料有限元模型，求解有限元方程可直接得到应力强度因子。计算结果与用其他方法得到的数据吻合，验证了方法的正确性，可用于双材料V型切口结构断裂特性计算分析。

关键词：双材料V型切口；渐进位移场；加料单元；过渡单元；应力强度因子

随着结合材料工程应用范围的不断扩大，因结合材料界面缺陷导致的结构失效问题日益引起人们的广泛关注。界面端部在结合材料中不可避免，而界面端部由于材料几何结构或工艺制作上的原因出现的V型切口，则是一种常见的界面缺陷表现形式。

Pageau等[1]应用Williams本征函数方法研究了结合材料V型切口和界面折点奇异性平面问题，给出了特征值为复数时位移和应力场角函数求解方法。Tan等[2]发展了一种计算应力强度因子的一维线性有限元方法。Gu等[3]给出了一种求解双材料V型切口奇异性指数的有限元方法，该方法通过设定切口端点渐进位移场或应力函数的分离变量解，应用变分原理将求解的问题转化为一个特征值问题，求解特征值问题可直接得到奇异性指数。随后，Pageau等[4]用类似的方法，通过给定极坐标下奇异位移场的位移模式，利用虚功原理将求解奇异性指数和角函数转化为一个特征值问题，求解特征方程可直接得到奇异性指数和位移角函数值，并将该方法推广到三维双材料V型切口问题[5]，Zhang等[6]用同样的方法提出了一种适用于幂硬化材料界面切口端点奇异场的非线性有限元方法。在上述研究基础上，平学成等[7-8]提出了基于位移的V型切口非协调元法，程长征等[9]用边界元方法对双材料V型切口应力奇异性进行了分析。王海涛[10]提出了一种分析不同材料V型切口应力奇异性的一维杂交有限元方法，通过扇形区域在角度方向上离散得到特征矩阵方程。

上述方法多以一维有限元特征矩阵计算特征值，应力强度因子的获取以应力杂交元和边界元方法为主，在计算网格前处理和扩展性方面，不便于推广到主流有限元程序中。为此，杨军辉等提出了一种基于加料有限元方法的双材料V型切口应力奇异性分析方法。目前，加料有限元方法在单相介质断裂[11]和界面裂纹问题中已得到应用[12]，但在双材料V型切口问题中还未见相关文献报道。

1双材料V型切口渐进位移场

1.1双材料V型切口特征值

双材料V型切口端点O(如图1所示)附近的应力和位移场可用Williams本征函数展开表示，在极坐标系中，Williams给出的应力函数为：

Φ(r,θ)=rλ+1f(θ)

(1)

图1　双材料V型切口Fig.1　Bi-material V-notch

Φ(r,θ)满足双调和方程▽4Φ(r,θ)=0，由此可得

f(θ)=VRVck

(2)

其中:VR=[sin(λ+1)θcos(λ+1)θsin(λ-1)θcos(λ-1)θ]，Vck=Q[Ck,1Ck,2Ck,3Ck,4]T，Ck,1、Ck,2、Ck,3、Ck,4为常系数项，由边界条件决定，λ为特征值，下标k代表第k种材料，Q为标准化系数。相应的应力和位移场可表示为：

(3)

将位移表示成矩阵向量的形式。

(4)

其中：μk为剪切模量；平面应变状态下κk=νk，平面应力状态下κk=νk/(1+νk)，νk为泊松比。在极坐标系下，应力自由边界条件和界面连续条件为：

(5)

将式(3)应力、位移表达式代入边界条件(5)中，得到线性齐次特征方程。

MVc=0

(6)

其中：M为各向同性弹性材料界面端V型切口特征矩阵，它与特征值λ、剪切模量μ、切口角θ1、θ2有关；Vc=[Vc1Vc2]T为解向量。式(6)有非零解的充要条件是特征矩阵M的行列式等于零，即

detM=0

(7)

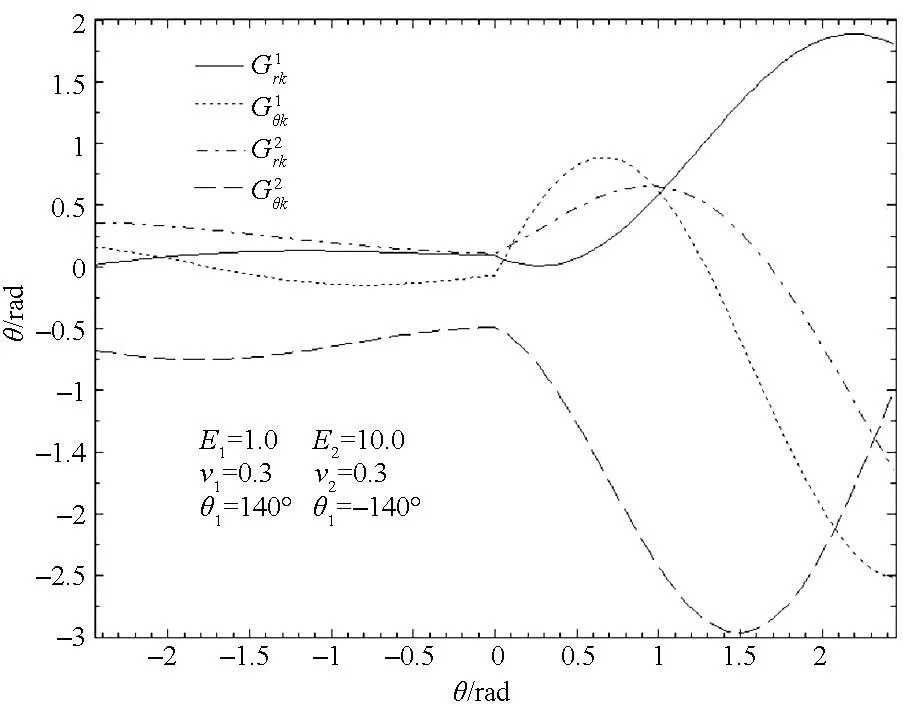
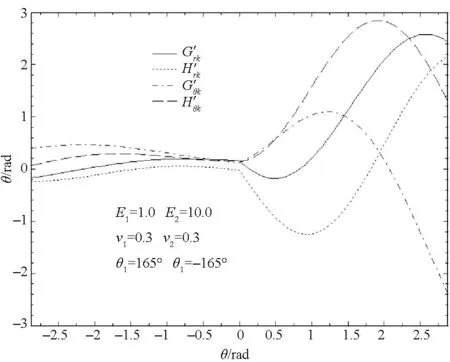
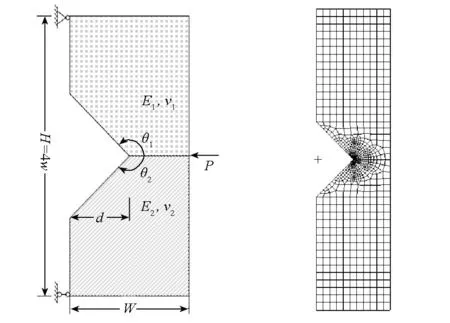
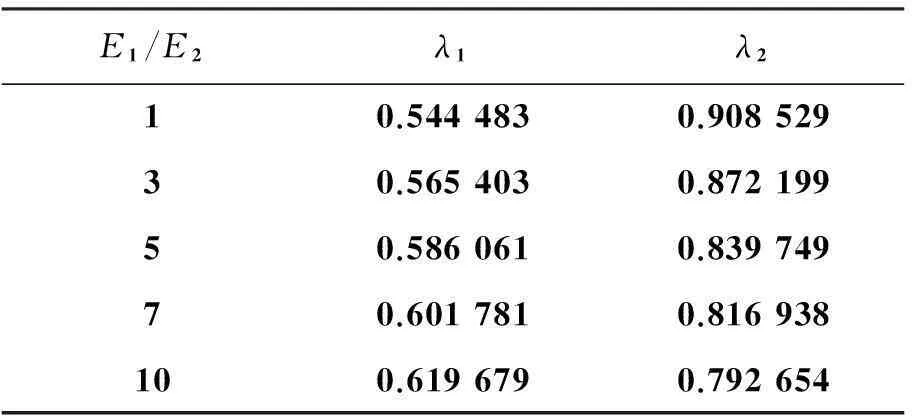
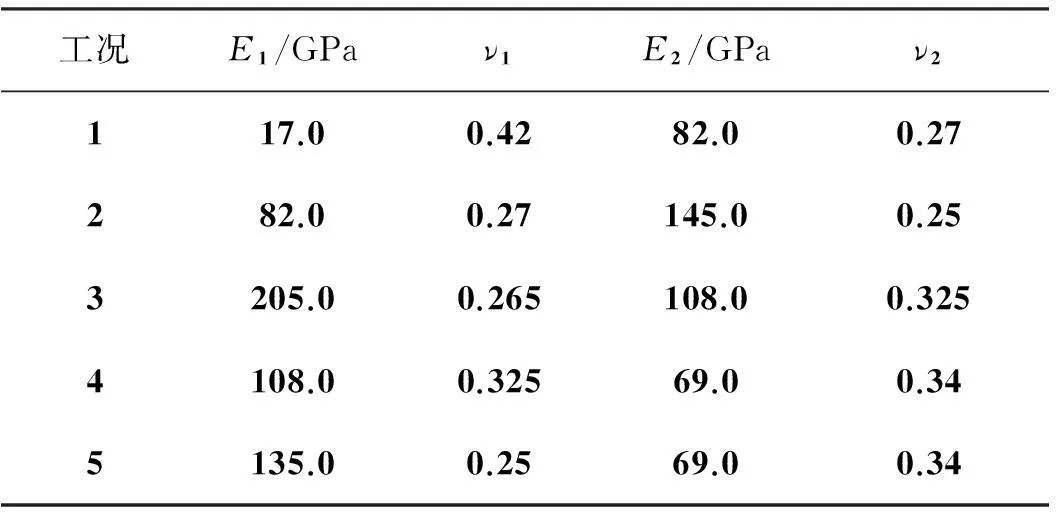
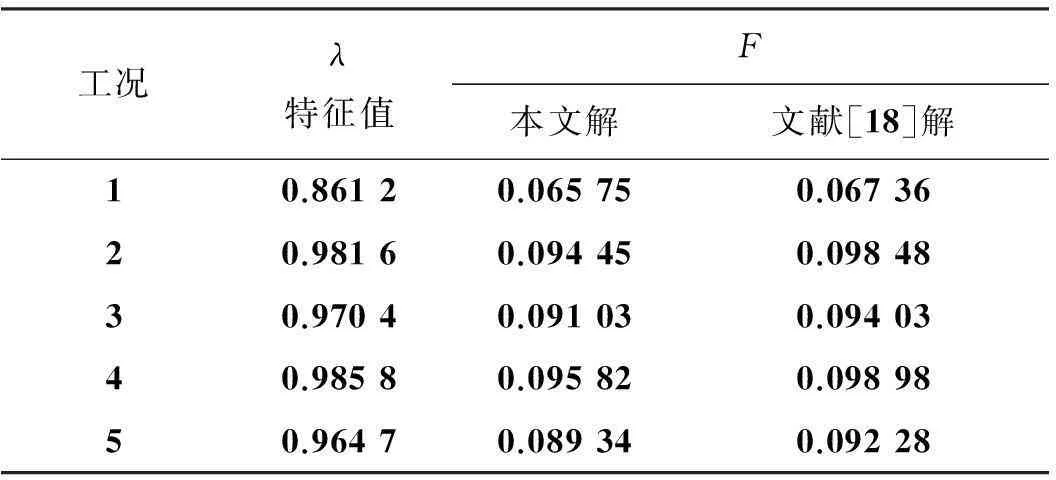
式(7)即为各向同性弹性材料界面端V型切口问题的特征方程，求解该方程可得到特征值λ。图2给出了平面应变状态下，E1=1.0，ν1=0.3，E2=10.0，ν2=0.3，θ1从90°变化到180°(θ1=-θ2)特征值变化规律。从计算结果可见，依据界面端切口材料参数、切口张开角的不同，在0

图2　特征值随切口角度的变化规律Fig.2　Variation of eigenvalue with V-notch surface angle

1.2特征值为实数时位移场角函数

当有两个实特征根时，渐进应力、位移场可表示为：

(8)

当特征值λ1，λ2为实数时，其对应的应力强度因子K1，K2是解耦的，根据通常的V型切口应力强度因子定义，可得：

(9)

将应力表达式(3)、解向量Vc代入式(9)中，可求得标准化系数Q与应力强度因子Kk之间的关系。

(10)

式(10)表示解向量标准化系数和应力强度因子之间的关系，Q1，Q2为：

(11)

将式(10)代入式(4)中，与式(8)比较后可得到极坐标下位移场角函数表达式。

(12)

图3　双材料V型切口位移场角函数(实特征值)Fig.3　Displacement field angular functions of bi-material V-notch (real roots)

图3为E1=1.0，ν1=0.3，E2=10.0，ν2=0.3，θ1=-θ2=140°时平面应变状态下位移场角函数曲线，此时特征值λ1=0.578 4，λ2=0.771 1。退化为均质材料V型切口时(E1=1.0，ν1=0.2，E2=E1，ν2=ν1)位移场角函数曲线如图4所示，计算结果和解析解[13]一致，表明本文方法得到的位移角函数是正确的。

图4　均质材料V型切口位移场角函数Fig.4　Displacement field angular functions of homogeneous material V-notch

1.3特征值为复数时的位移场角函数

当特征方程(7)有一对共轭复根时，应力强度因子K1，K2之间是耦合在一起的，此时界面端V型切口应力强度因子定义为：

(13)

应力和位移表示[1]为：

(14a)

(14b)

其中：β+iζ=λ，i为虚数单位；φ，α为标准化参数；角函数hijk(θ)，gik(θ)由特征值、特征方程基础解向量和应力、位移表达式得到。图5给出了E1=1.0，ν1=0.3，E2=10.0，ν2=0.3，θ1=-θ2=30°，平面应变状态下特征值λ=0.548 5±0.072 4i时位移场角函数曲线。当θ1=-θ2=180°时，双材料V型切口退化为界面裂纹，文献[14]给出了直角坐标系下界面裂纹尖端位移场角函数解析解，通过坐标变换可得到极坐标系下的解析解。由图6可见本文解与文献[14]解析解一致，表明本文的结果是正确的。

图5　双材料V型切口位移场角函数(复特征值)Fig.5　Displacement field angular functions of bi-material V-notch (complex roots)

图6　双材料界面裂纹尖端位移场角函数Fig.6　Displacement field angular functions of bi-material interfacial crack

对于双材料V型界面切口，当特征值为复数时，与双材料界面裂纹相似，应力和位移场角函数中仍包含riζ项，因此，其理论解同样会出现应力振荡与位移相互嵌入的不合理现象。作为V型界面切口的一个特例，Shih等[15]和Rice[16]对界面裂纹中这一现象进行研究，许金泉[17]对其做了比较全面的总结分析，此处不再赘述。

2加料有限元方程

2.1加料切口单元位移函数

以位移表达式(8)为例，对其进行坐标变换，得到直角坐标系o′x′y′下的位移场，与位移式(14a)除表达形式略有不同外，变换过程完全相同。

(15)

其中，fij(r,θ)(i,j=1,2)表示直角坐标系下的切口尖端角函数，形式为：

(16)

对8节点四边形等参元，在常规单元位移模式中加入式(15)后，可得加料切口单元位移模式。

(17)

其中，ui(i=1,2)分别表示总体坐标系下加料切口单元x，y方向的位移，αij为广义坐标，ξ，η分别为单元局部坐标系的坐标轴，fij(r,θ)如式(16)所示。将8节点四边形等参元的节点局部坐标(ξi,ηi)代入式(17)中，可得到广义坐标αij的表达式，再将得到的广义坐标回代到式(17)中，得到以节点位移和应力强度因子表示的加料切口单元位移函数。

(18)

2.2过渡单元位移函数

在加料切口单元位移模式的基础上，引入一个调整函数Z(ξ,η)来构造过渡单元，以消除加料单元和常规单元之间因位移模式引起的位移不协调问题，从而保证有限元解的收敛，提高计算精度。

(19)

式(19)中调整函数Z(ξ,η)须满足：Z(ξ,η)在过渡单元与加料切口单元交界边上为1，在过渡单元与常规单元交界边上为0，实现从加料切口单元到常规单元的协调过渡。采用相对简单的线性调整函数。

(20)

在有限元分析过程中，需要根据过渡单元与加料切口单元的连接方式以及过渡单元的局部坐标系，选择适当的表达式。

2.3有限元方程

为了便于推导有限元方程，将加料单元、过渡单元位移模式统一写为：

(21)

(22)

对于加料单元Z(ξ,η)≡1，过渡单元按式(17)取值，将位移向量式(21)代入位移应变关系ε=Lu中，得到：

(23)

其中：B表示单元常规应变矩阵；Bk则是由于加料界面切口单元位移模式中引入切口尖端位移项而产生的附加项，称之为附加应变矩阵。将式(23)代入单元应力应变关系式σ=Dε中，应用总体势能泛函，得到：

(24)

其中：b为体力，P为面力，Ω表示求解域，Γ为面力积分边界，D为材料矩阵。取值依据界面两侧材料具体参数确定，可得到：

(25)

其中：U为总体位移列阵，K为应力强度因子列阵。其他符号表达式为：

(26)

其中：下标ns表示加料单元数量，nt表示过渡单元数量，no表示常规单元数量，上标e表示单元。根据最小势能原理，式(25)分别对U，K变分，得到有限元方程为：

(27)

3算例分析

3.1算例1

具有V型切口的三点弯曲梁试件，由两种材料构成，如图7所示。试件厚度B=1 mm，切口深度d=5 mm,宽度w=10 mm，长度H=4w, 切口角θ1=-θ2=135°，集中力P=1 N。构成试件的两种材料具有相同的泊松比，ν1=ν2=0.3，弹性模量E2=1 MPa,两种材料弹性模量比E1/E2分别为1，3，5，7，10，按平面应力问题计算不同弹性模量比下的应力强度因子。

图7　算例1模型和有限元网格示意图Fig.7　Schematic of geometry and mesh for example 1

有限元模型共划分为856个8节点四边形单元，2713个节点，切口端点加料单元尺度为5.4×10-2w，在切口尖端设置4个加料单元、8个过渡单元。有限元网格划分如图7所示，切口尖端加料单元和过渡单元配置如图8所示。计算单元刚度矩阵时，加料单元和过渡单元采用10×10高斯积分，常规单元采用3×3高斯积分。

图8　算例1网格划分和加料单元配置方案Fig.8　Meshes and enriched element scheme of example 1

特征值计算结果见表1，由表1可见各工况下两个特征值均为实数，随着E1/E2比值的增大，λ1逐渐增大而λ2逐渐减小。由表2应力强度因子计算结果可知，随着界面两侧材料差异性的增强，两种模态的应力强度因子的绝对值是增大的。

表1　算例1特征值计算结果

表2算例1应力强度因子计算结果

Tab.2Stress intensity factors of example 1

E1/E2F1F2本文解文献[9]解本文解文献[9]解12.1402.10100032.44382.3935-0.56581-0.647052.83912.7857-0.92665-1.008973.24113.1793-1.2425-1.2938103.87663.7993-1.7044-1.6886

文献[9]采用边界元方法对相同的问题进行了计算，得到了应力强度因子数值解，并标准化处理为Fi=KiBwλi/(6P)。为了便于对比，本文应力强度因子采用同样的处理方法，各种工况下应力强度因子计算结果列于表2。可见各工况下本文结果与边界元方法计算结果吻合，表明本文方法的正确性与有效性。

3.2算例2

由两种弹性材料构成的直角界面端平板，平板高为2H，宽W，受单向均匀分布拉伸载荷σ0作用，如图9所示。为便于和相关文献结果对比，结构、载荷和材料属性与文献[18]一致，取H=16 mm，W=8 mm,选用铅、轧制锌、碳钢、轧制纯铜、铝、灰口铸铁和白口铸铁等材料形成5种材料组合工况，材料属性见表3。

图9　算例2模型和有限元网格示意图Fig.9　Schematic of geometry and mesh for example 2

根据载荷和几何对称性，取1/2建立有限元模型，共划分为720个8节点四边形单元，2287节点，界面端部设置2个加料单元，6个过渡单元,单元尺度为1.5×10-2w,界面端部加料单元和过渡单元配置如图9所示。计算单元刚度矩阵时，加料单元和过渡单元采用10×10高斯积分，常规单元采用3×3高斯积分。

表3　材料参数

文献[18]采用边界元方法，通过应力外插求取应力强度因子，并对应力强度因子做无量纲处理F=K/(σ0w1-λ)。本文应力强度因子计算结果以及和文献[15]对比情况见表4，由表4可知，应力强度因子随着特征值增大而增大，两种方法得到的结果变化趋势是一致的，并且数值吻合良好，差别很小，表明本文的计算方法是正确有效的。

表4　算例2应力强度因子计算结果

4结论

应用Willams本征函数展开和线性变换相结合的方法得到双材料V型切口渐进位移场。与复势函数法等方法相比，该方法推导过程及最终表达形式采用矩阵向量的形式，相对而言较为简洁直观，适于数值计算。

将双材料V型切口渐进位移场加入到常规等参元位移模式中构造了加料单元和过渡单元的位移表达式，推导了加料有限元方程，求解有限元方程得到应力强度因子。通过带V型缺口的双材料三点弯曲梁试件和直角界面端平板受拉两个算例，表明本文方法的正确性。该方法不仅能得到双材料V型切口端点附近的应力场和位移场角函数值，并且能通过求解加料有限元方程直接得到广义应力强度因子，避免了外插法需要对应力场二次处理才能得到应力强度因子的不便以及由此带来的精度损失，是对双材料V型切口进行应力奇异性分析的一种有效方法。

参考文献(References)

[1]Pageau S S, Gadi K S,Biggers S B Jr,et al. Standardized complex and logarithmic eigensolutions forn-material wedges and junctions[J]. International Journal of Fracture, 1996, 77(1):51-76.

[2]Tan M A, Meguid S A.Analysis of bimaterial wedges using a new singular finite element[J]. International Journal of Fracture, 1997, 88(4):373-391.

[3]Gu L, Belytschko T.A numerical study of stress singularities in a two-material wedge [J]. International Journal of Solids and Structures, 1994, 31(6):865-889.

[4]Pageau S S, Joseph P F,Biggers S B Jr.Finite element analysis of anisotropic materials with singular inplane stress fields [J].International Journal of Solids and Structures, 1995, 32(5):571-591.

[5]Pageau S S, Biggers S B Jr.A finite element approach to three dimensional singular stress states in anisotropic multi-material wedges and junctions [J].International Journal of Solids and Structures, 1996, 33(1):33-47.

[6]Zhang N S, Joseph P F.A nonlinear finite element eigen analysis of singular plane stress fields in bimaterial wedges including complex eigenvalues[J]. International Journal of Fracture, 1998, 90(3):175-207.

[7]平学成, 谢基龙, 陈梦成, 等.各向异性两相材料尖劈奇性场的非协调元分析[J]. 力学学报, 2005, 37(1): 24-31.

PING Xuecheng, XIE Jilong, CHEN Mengcheng, et al.Anon-confirming finite element analysis of singular fields in prismatic anisotropic bimaterial wedges[J]. Acta Mechanica Sinica, 2005, 37(1): 24-31.(in Chinese)

[8]平学成, 陈梦成,谢基龙.复合材料尖劈和接头端部奇性场的反平面问题研究[J]. 固体力学学报, 2005, 26(2):193-198.

PING Xuecheng, CHEN Mengcheng,XIE Jilong. Singular stress states in tips of anisotropic multi-material wedges and junction subjected to antiplane shear[J]. Acta Mechanica Solid Sinica, 2005, 26(2):193-198.(in Chinese)

[9]Cheng C Z, Niu Z R, Recho N.Analysis of the stress singularity for a bi-material V-notch by the boundary element method[J]. Applied Mathematical Modelling, 2013, 37(22): 9398-9408.

[10]王海涛.分析不同材料界面应力奇异性的一维杂交有限元方法[J]. 工程力学, 2009, 26(2):21-26.

WANG Haitao.A one-dimensional hybrid finite element method for the analysis of stress singularities at bimaterial interface [J]. Engineering Mechanics,2009, 26(2):21-26.(in Chinese)

[11]段静波,雷勇军.线粘弹性材料中三维裂纹问题的加料有限元法[J]. 国防科技大学学报, 2012, 34(3): 6-11.

DUAN Jingbo, LEI Yongjun.The enriched finite element method for 3-D fracture problems in viscoelastic materials[J]. Journal of National University of Defense Technology, 2012, 34(3): 6-11.(in Chinese)

[12]Ayhan A O, Kaya A C, Nied H F.Analysis of three-dimensional interface cracks using enriched finite elements[J]. International Journal of Fracture, 2006, 142(3):255-276.

[13]Carpenter W C.Mode I and Mode II stress intensities for plates with cracks of finite opening[J]. International Journal of Fracture, 1984, 26(3): 201-214.

[14]Chen E P.Finite element analysis of a bimaterial interface crack[J]. Theoretical and Applied Fracture Mechanics, 1985, 3(3): 257-262.

[15]Shih C F,Asaro R J.Elastic-plastic analysis of cracks in biomaterial interface[J].Journal of Applied Mechanics, 1988, 55(2): 299-316.

[16]Rice J R.Elastic fracture mechanics concepts for interfacial cracks[J]. Journal of Applied Mechanics,1988, 55(1): 98-103.

[17]许金泉.界面力学[M].北京:科学出版社,2006.

XU Jinquan.The mechanics of interface[M]. Beijing:Science Press, 2006. (in Chinese)

[18]唐亮,许金泉.直角结合异材界面端应力强度系数的经验公式[J]. 力学季刊, 2005, 26(1): 96-101.

TANG Liang, XU Jinquan.An empirical formula for stress intensity coefficient of orthogonal bonded materials near interface end[J]. Chinese Quarterly of Mechanics,2005, 26(1): 96-101.(in Chinese)

Enriched finite element analysis of stress intensity factors of bi-material V-notch

YANGJunhui1,2,HANJunli2,LEIYongjun1,MENGShangyang2

(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China；2.Beijing Institute of Special Electromechanical Technology, Beijing 100012, China)

Abstract：The V-notch asymptotic displacement field was derived through an approach based on the Williams’ series expansion and linear algebraic transforms. By incorporating the displacement expressions to the common isoparametric elements, the enriched and transition element displacement model were obtained, and then the enriched finite element equation was derived consequently. The enriched finite element model for a V-notched bi-material three-point bending beam and an orthogonal bonded materials interface end plane problem were constructed. The stress intensity factors can be solved directly from the finite element equation. Comparisons between the results and the published data computed with other algorithm indicate that the present method is correct and can be used to analyze the fracture property of the V-notched bi-material structure.

Key words：bi-material V-notch; asymptotic displacement field; enriched element; transition element; stress intensity factor

中图分类号：O346.1

文献标志码：A

文章编号：1001-2486(2016)01-156-07

作者简介：杨军辉(1979—)，男，河北深泽人，博士研究生，E-mail：yangjun_hui@126.com;雷勇军(通信作者)，男，教授，博士，博士生导师，E-mail：leiyj108@nudt.edu.cn

基金项目：国家自然科学基金资助项目(11272348)

*收稿日期：2015-02-02

doi:10.11887/j.cn.201601025

http://journal.nudt.edu.cn