多脉冲导弹可达域优化方法设计与分析*

明　超，孙瑞胜，梁　卓，白宏阳

(1.南京理工大学 能源与动力工程学院， 江苏 南京　210094；

2. 中国运载火箭技术研究院， 北京　100076)



多脉冲导弹可达域优化方法设计与分析*

明超1，孙瑞胜1，梁卓2，白宏阳1

(1.南京理工大学 能源与动力工程学院， 江苏 南京210094；

2. 中国运载火箭技术研究院， 北京100076)

摘要：为了更合理地制定导弹的战术指标和作战任务规划，对多脉冲导弹可达域进行研究。通过引入加权的纵程和横程的组合性能指标函数，将可达域的优化问题转化为最优控制问题，建立以飞行攻角和侧滑角为双优化设计变量的多阶段多约束优化模型，采用hp自适应伪谱法对其进行求解，并着重分析多脉冲导弹发动机参数和终端约束条件对导弹可达域的影响。仿真结果表明，hp自适应伪谱法能有效解决多阶段多约束的多脉冲导弹可达域优化问题，且多脉冲导弹脉冲发动机时间间隔越小，推力比越大，装药比越小，导弹的可达域越大，相比于终端速度对可达域的影响，终端弹道倾角对可达区域的影响较小。

关键词：多脉冲导弹；可达域优化；hp自适应伪谱法；发动机参数；终端约束

多脉冲导弹可实现推力的随机控制，根据飞行任务的需求对发动机不同脉冲之间的时间间隔进行控制，有效地改善了其机动性能，提高导弹的生存能力[1-2]。可达域可用于衡量飞行器的机动能力，也可为飞行任务的确定提供有力支持[3-4]。多脉冲导弹飞行包络大，飞行环境比较复杂，为更准确地制定多脉冲导弹不同作战条件下任务规划，因此对多脉冲导弹可达域进行研究具有重要的理论意义和工程价值。

可达域是指在给定初始条件及终端条件下，纵向和横向的最大机动范围，是评价飞行器总体性能的一项重要指标[5]，备受国内外学者关注[6-9]。雍恩米[6]利用Gauss伪谱法对高超声速滑翔式再入飞行器的再入轨迹进行了优化，采用简单的连线方式分析飞行器可达区域。Amitabh[7]利用加速度剖面建立一种近实时的可达区域计算方法。胡正东[8]利用组合优化算法分别对典型落点经度下的最大横程进行优化设计，从而确定天基对地武器的打击覆盖范围。冯必鸣[9]基于飞行器纵程与横程近似符合椭圆分布的假设，建立了飞行器再入后地球面可达区域边界的快速计算方法。总的来说，国内外对此领域的研究主要集中在再入飞行器在可达区域的优化和快速估算，而对多飞行阶段多脉冲导弹可达区域研究及影响因素的研究很少涉及。为此，以某双脉冲导弹为例进行可达域分析研究，建立以多脉冲导弹攻角和侧滑角为双优化设计变量的多阶段多约束弹道优化模型，引入加权的组合性能指标函数，将可达域优化问题转化为最优控制问题，采用hp自适应伪谱法进行求解，并着重分析了多脉冲发动机参数及终端弹道参数对脉冲导弹可达域的影响。

1优化模型

1.1工作过程

以双脉冲导弹为例，其飞行过程可分为四个阶段。第一阶段：Ⅰ脉冲发动机工作，将导弹加速至一定的高度和速度后关机。第二阶段：Ⅰ，Ⅱ脉冲发动机工作间隔，导弹无动力飞行。第三阶段：导弹飞行至空气阻力较低的高空，Ⅱ脉冲发动机工作，对导弹进行二次加速。第四阶段：导弹无动力滑翔飞行直至命中目标。工作过程示意图如图1所示。

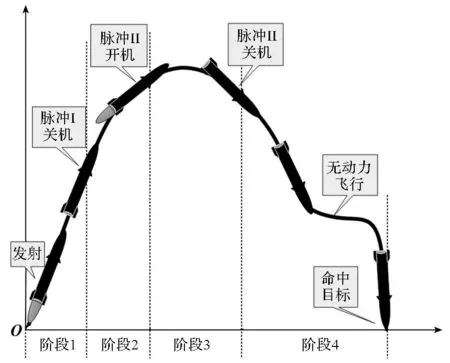
图1　工作过程示意图Fig.1　Schematic diagram of work process

1.2动力学模型

为研究问题方便，假设地球为均质圆球，且忽略地球自转影响，基于以上假设，多脉冲导弹质点的动力学方程[10]为：

(1)

式中：v为速度；θ为弹道倾角；φv为弹道偏角；x，y和z分别为导弹纵程，射高和横程；m为质量；P为推力；α，β分别为飞行攻角和侧滑角；X=qSCx，Y=qSCy和Z=qSCz分别为阻力，升力和侧向力，由动压q=0.5·ρ·v2和气动特性决定；Cx，Cy和Cz是Ma和α的函数，可由吹风试验和数值计算获得；mc为质量流量；ρ为大气密度，其表达式为ρ=1.752e-y/6700；ε(α,β)=0为攻角和侧滑角的控制方程。

1.3发动机模型

多脉冲导弹采用双脉冲固体火箭发动机，保持发动机的总冲I不变，即总装药量M一定，设Ⅰ，Ⅱ脉冲发动机装药量比为φ，则Ⅰ，Ⅱ脉冲装药量分别为：

M1=M·φ/(1+φ)，M2=M/(1+φ)

(2)

如果选用相同的推进剂，Ⅰ，Ⅱ脉冲发动机的总冲分别为：

I1=I·φ/(1+φ)，I2=I/(1+φ)

(3)

假设Ⅰ，Ⅱ脉冲发动机的推力F1和F2大小不变，则Ⅰ，Ⅱ脉冲的质量流量分别为：

mc1=M1·F1/I1，mc2=M2·F2/I2

(4)

1.4约束条件

1)边界约束。多脉冲导弹的初始状态为：

v(t0)=0 m/s，θ(t0)=60°，φv(t0)=0°，

x(t0)=0 m，y(t0)=0 m，z(t0)=0 m

为保证多脉冲导弹的攻击效果，其终端状态也应满足一定的约束条件：

v(tf)=vf，θ(tf)=θf，y(tf)=0 m

2)控制约束。多脉冲导弹的飞行攻角α和侧滑角β的约束条件为：

-15°≤α≤15°，-10°≤β≤10°

3)连接点约束。多脉冲导弹具有多飞行阶段，为保证四个阶段平滑过渡，上一阶段结束时刻的状态量和控制量应与下一阶段开始时刻的对应相等，约束条件为：

t0(i+1)=tf(i)，s0(i+1)=sf(i)，

u0(i+1)=uf(i)，(i=1,2,3)

式中，i表示双脉冲导弹飞行的第i阶段，t表示时间，s表示状态量，u表示控制量，下标0表示开始，下标f表示结束。

4)路径约束。考虑导弹的防热要求，动压q必须在一定的范围内：

5 kPa≤q≤450 kPa

为满足导弹结构设计要求，法向过载ny应满足一定的约束条件：

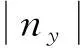
1.5性能函数

根据多脉冲导弹可达域的特点，引入权重因子w，定义加权的纵程和横程的组合性能函数为：

J=w·(±xf)+(1-w)·(±zf)

(5)

式中，w∈[0,1]为权重因子，w=1时对应最大和最小纵程点，w=0时对应最大和最小横程点，w取其他值对应的是可达域边界上的其他点，可达域的计算精度取决于w的取值密度。这样，通过引入加权的组合性能函数，将多脉冲导弹可达域优化问题转化为求解满足设计约束的最优控制问题。

2优化方法

所提优化方法采用hp自适应伪谱法，是将Legendre伪谱法[11-12]与hp自适应法[13]进行结合，将状态量和控制变量在一系列的Legendre-Gauss-Lobatto点上进行离散，并以这些离散点为节点构造Lagrange插值多项式来逼近状态量和控制量，将微分方程约束转化为代数约束，指标函数中的积分项由Gauss-Lobatto积分计算，终端状态由初始状态对右端函数的积分获得，从而将最优控制问题转化为具有一系列代数约束的非线性规划(Non-Linear Programming,NLP)问题。当某一离散区间的计算精度不满足要求时，由hp自适应方法对该区间的配点数和全局插值多项式阶次进行自适应调整。

2.1最优控制问题离散

Legendre伪谱法对最优控制问题的离散过程如下：

最优控制问题的时间区间为[t0,tf]，将时间区间转化为Legendre伪谱法的时间区间[-1，1]，对时间变量t作如下变换：

τ=2t/(tf-t0)-(tf+t0)/(tf-t0)

(6)

当配点数为K时，以K个Lagrange插值多项式Li(τ)为基函数来近似状态量和控制量的时间历程，即：

(7)

(8)

对式(6)进行求导可得状态量导数的近似表达式为：

(9)

从而将动力学方程约束转化为代数约束，即：

(10)

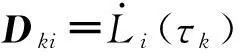
目标函数可近似表示为：

J=φ(X0,t0,Xf,tf)

(11)

路径约束表示为：

C(Xk,Uk,τk;t0,tf)≤0

(12)

边界约束条件可近似表示为：

φ(X0,t0,Xf,tf)=0

(13)

基于上述离散过程，将最优控制问题转化为非线性规划问题，对于离散的NLP问题采用内点法C++软件包[14]进行求解。

2.2hp自适应更新判定准则

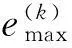
2.3hp自适应更新方式判定准则

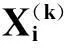
(14)

(15)

如果rkrkmax，则增加网格的配点数目。其中，rkmax>0为用户自定义参数。

2.4hp自适应更新变量计算

1)更新后插值多项式的阶次Dnew

(16)

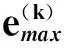
2)更新后配点数Nnew

(17)

式中，Nnew为更新后网格内的配点数，B为常值，决定网格数的增长速度。

2.5hp自适应伪谱法流程

hp自适应伪谱法计算步骤如下，其流程图如图2所示。

1)初始化网格；

2) 利用Legendre伪谱法将最优控制问题离散，转化为NLP问题；

3)采用内点法求解非线性规划问题；

4)若性能指标函数不是最优, 则更新控制变量并返回至步骤3；

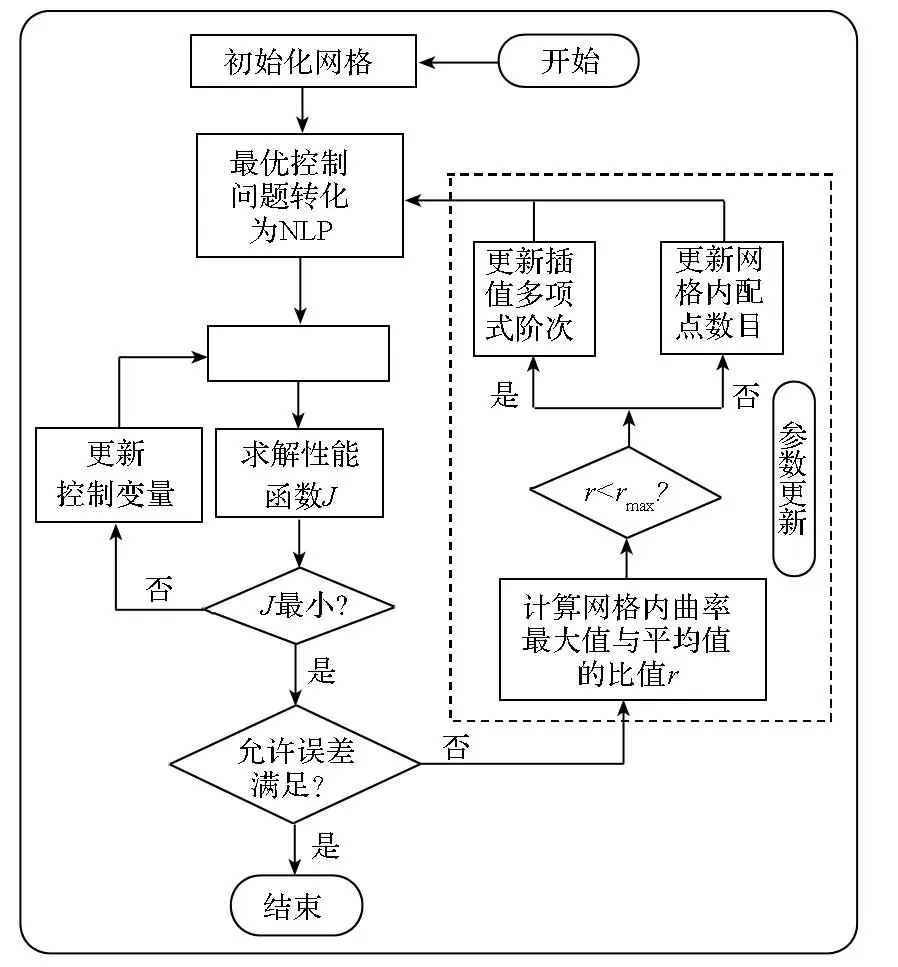
图2　hp自适应伪谱法流程图Fig.2　Hp-adaptive pseudo-spectral method process

3仿真结果分析

3.1仿真条件设置

以某双脉冲导弹为例，采用hp自适应伪谱法对其可达域进行优化设计。导弹的总质量m0为4000 kg，燃料的总质量m1为2200 kg，发动机总冲量I为5500 kN·s，不同Ⅰ、Ⅱ脉冲发动机装药比下的I脉冲推力值F1如表1所示，II脉冲推力值可根据推力比进行计算，分别研究脉冲时间间隔、装药比、推力比、落速和落角对多脉冲导弹可达域的影响。

表1　不同装药比下的I脉冲推力值

3.2时间间隔的影响

仿真条件：Ⅰ，Ⅱ脉冲装药比选为2 ∶1，推力比为1 ∶1，多脉冲导弹终端速度的约束条件为vf=700 m/s，终端的弹道倾角约束条件为θf≤-80°。研究分析Ⅰ，Ⅱ脉冲的时间间隔分别为20 s，40 s和60 s情况下的可达域，计算的终端位置参数如表2所示，各脉冲时间间隔下的可达域分布情况如图3所示。

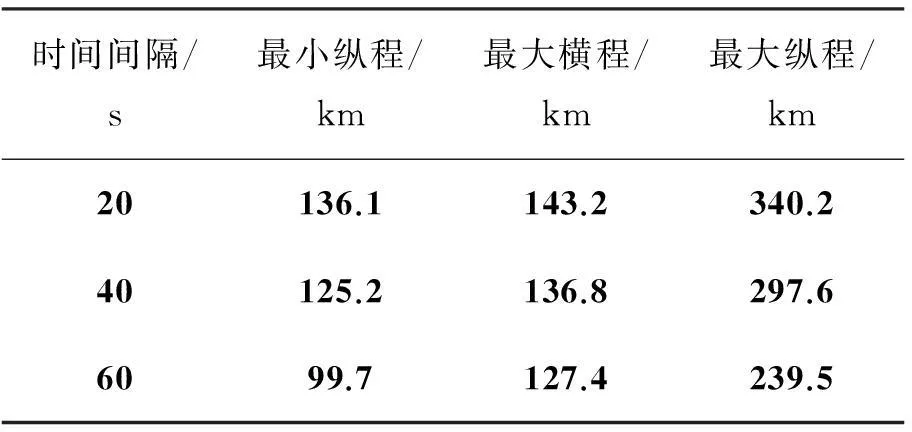
表2　不同时间间隔的终端位置参数

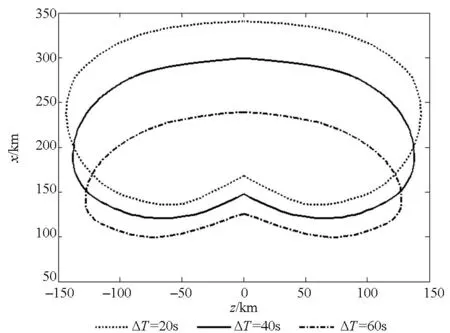
图3　不同时间间隔的可达区域Fig.3　Footprint under different pulse interval time

由仿真结果可以看出，可达域是关于纵程对称分布。如表2所示，时间间隔为20 s时在纵向跨度为204.1 km，横向跨度为286.4 km；60 s时在纵向跨度为139.8 km，横向跨度为254.8 km。如图3所示，可达域随着Ⅰ，Ⅱ脉冲时间间隔的增加而逐渐收缩，并且有向下平移的趋势。这是因为时间间隔越小，导弹飞行高度越高，穿越稀薄大气消耗的能量就越小，更有助于导弹增加射程。可见，多脉冲导弹Ⅰ，Ⅱ脉冲时间间隔对其可达域有着很大的影响，适当调节时间间隔可使多脉冲导弹具有更强的机动能力。

3.3装药比的影响

仿真条件：Ⅰ，Ⅱ脉冲推力比为1 ∶1，时间间隔为20 s，多脉冲导弹终端速度的约束条件为vf=700 m/s，终端的弹道倾角约束条件为θf≤-80°，研究分析Ⅰ，Ⅱ脉冲的装药比分别为2 ∶1，1 ∶1和1 ∶2情况下的可达域，计算的终端位置参数如表3所示，各脉冲装药比下的可达域分布情况如图4所示。

表3　不同装药比的终端位置参数

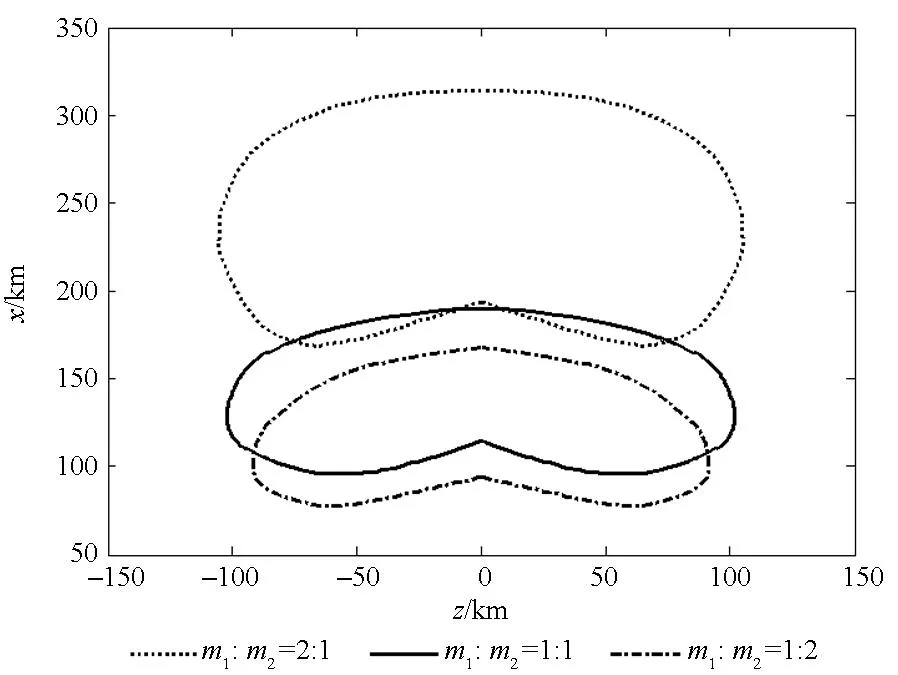
图4　不同装药比的可达区域Fig.4　Footprint under different mass radio

由仿真结果可以看出，可达域是关于纵程对称分布。如表3所示，装药比为2 ∶1时在纵向跨度为145.8 km，横向跨度为210.2 km；装药比为1 ∶2时在纵向跨度为78.0 km，横向跨度为182.8 km。如图4所示，可达域随着Ⅰ，Ⅱ脉冲装药比的减小而逐渐收缩，并且有向下平移的趋势。这是因为装药比越大，Ⅰ脉冲发动机推力越大，导弹能够以较短的时间到达阻力较小的高空，阻力消耗小，有利于增加导弹机动能力，并由此得出多脉冲导弹Ⅰ，Ⅱ脉冲装药比对导弹的可达域有着重要的影响。

3.4推力比的影响

仿真条件：Ⅰ，Ⅱ脉冲装药比为2 ∶1，时间间隔为20 s，多脉冲导弹终端速度的约束条件为vf=700 m/s，终端的弹道倾角约束条件为θf≤-80°，研究分析Ⅰ，Ⅱ脉冲的推力比分别为3 ∶1，2 ∶1和1 ∶1情况下的可达域，计算的终端位置参数如表4所示，各脉冲装药比下的可达域分布情况如图5所示。

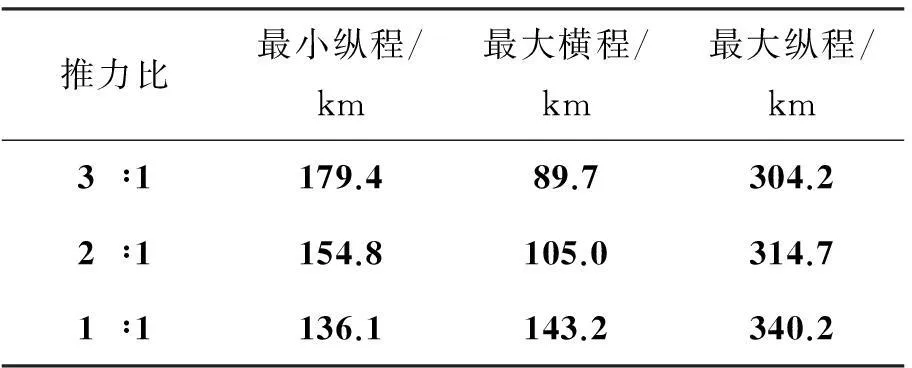
表4　不同推力比的终端位置参数

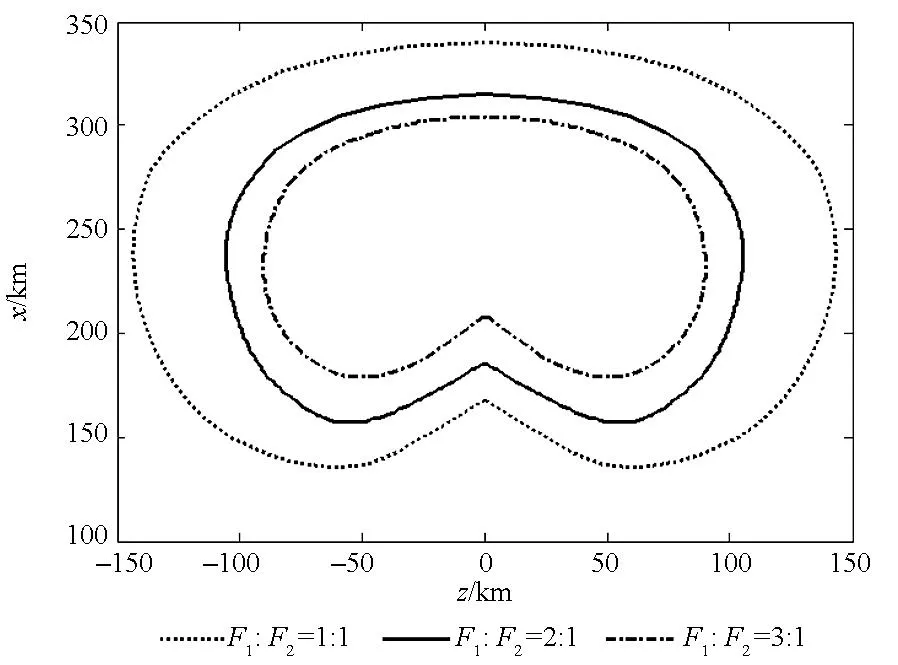
图5　不同推力比的可达区域Fig.5　Footprint under different thrust radio

由仿真结果可以看出，可达域是关于纵程对称分布。如表4所示，推力比为3 ∶1时在纵向跨度为124.8 km，横向跨度为179.4 km；装药比为1 ∶1时在纵向跨度为204.1 km，横向跨度为286.4 km。如图5所示，可达域随着Ⅰ，Ⅱ脉冲推力比的增加而逐渐收缩。这是因为推力比越小，Ⅱ脉冲发动机推力越大，二次推力加速时可以达到更高的高度，在空气密度较低的高空阻力消耗小，增程的效果越大，并由此得出多脉冲导弹Ⅰ，Ⅱ脉冲装药比越小，多脉冲导弹的作战空间更广阔。

3.5落速的影响

仿真条件：Ⅰ，Ⅱ脉冲装药比为2 ∶1，推力比为1 ∶1，时间间隔为20 s，多脉冲导弹终端的弹道倾角约束条件为θf≤-80°，研究分析落速vf的约束条件分别为600 m/s，700 m/s和800 m/s情况下的可达域，计算的终端位置参数如表5所示，各落速条件下的可达域分布情况如图6所示。

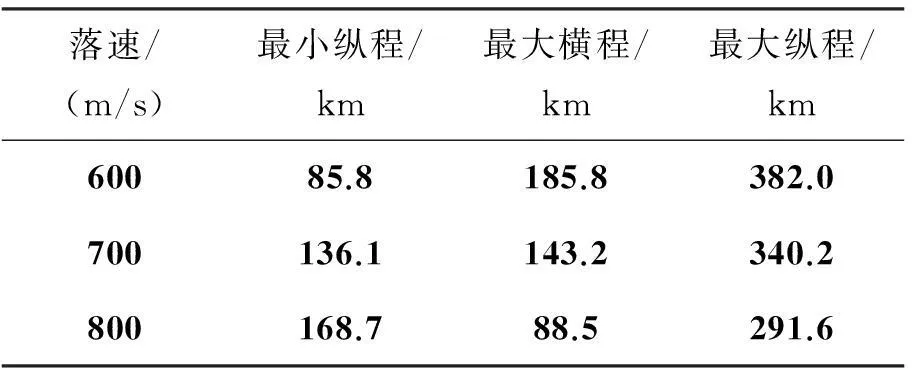
表5　不同落速的终端位置参数

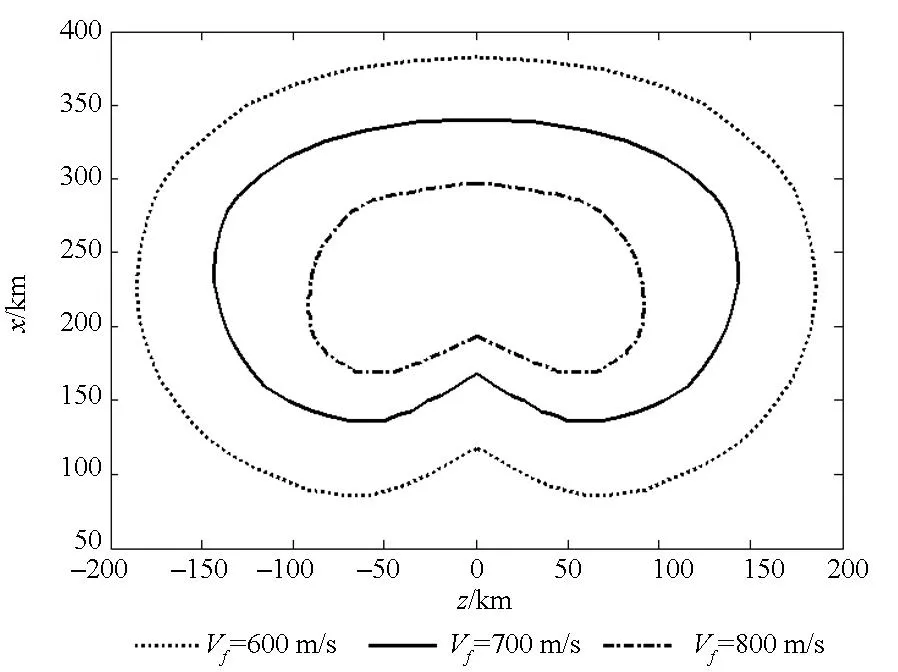
图6　不同落速的可达区域Fig.6　Footprint under different final velocity

由仿真结果可以看出，可达域是关于纵程对称分布。如表5所示，落速由600 m/s增加到800 m/s，多脉冲导弹可达域纵向跨度减小173.3 km，横向跨度减小了194.6 km。如图6所示，可达域随着落速的增加而逐渐收缩。这是因为终端速度的不同是飞行过程中的能量损失不同导致的，若要增加落速，则需要减小飞行距离和飞行时间，从而减少阻力做功，因此，多脉冲导弹所能达到的终端极限距离与落速成反比。所以，落速对导弹的可达域影响很大，若总体设计需要，调整终端速度约束，必须考虑对可达域的影响，并且要根据实际的飞行任务要求选择合适的终端速度约束以满足区域覆盖打击的设计要求。

3.6落角的影响

仿真条件：Ⅰ，Ⅱ脉冲装药比为2 ∶1，推力比为1 ∶1，时间间隔为20 s，多脉冲导弹终端速度的约束条件为vf=700 m/s，研究分析落角θf的约束条件分别为-60°，-70°和-80°情况下的可达域，计算的终端位置参数如表6所示，各落角条件下的可达域分布情况如图7所示。

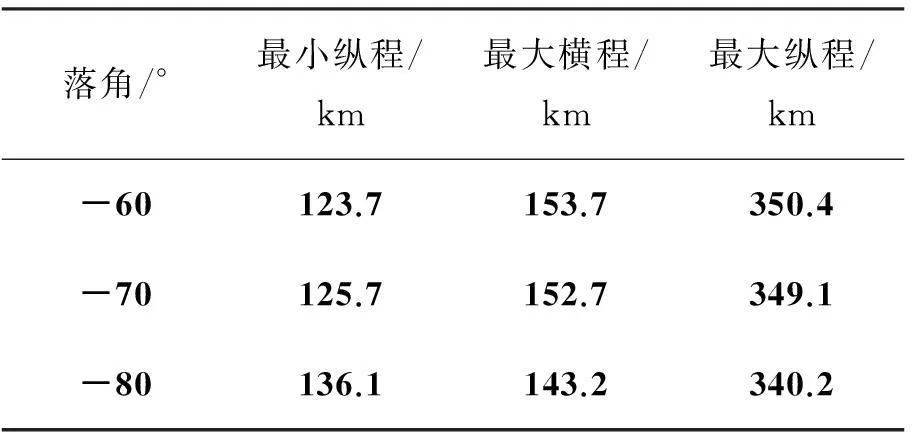
表6　不同落角的终端位置参数

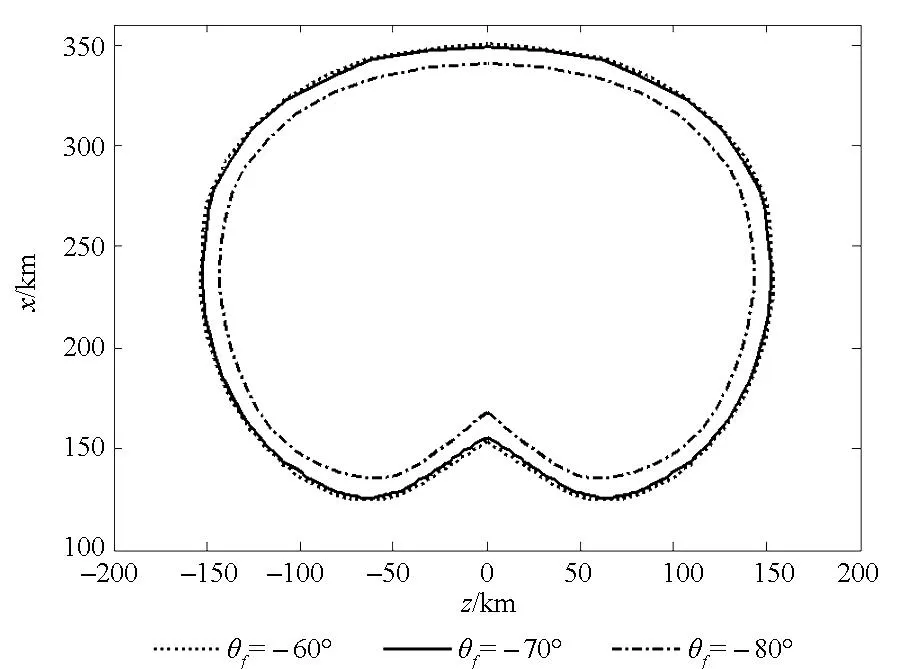
图7　不同落角的可达区域Fig.7　Footprint under different impact angle

由仿真结果可以看出，可达域是关于纵程对称分布。如表6所示，落角为-60°和-70°时在纵向跨度和横向跨度区别不大，分别为225 km和305 km左右；落角为-80°时在纵向跨度和横向跨度减小了约为20 km。如图7所示，三种落角约束条件下的多脉冲导弹可达域差别不大。这是因为三种情况下终端速度约束相同，在整个飞行过程中能量损失基本相同，因此，多脉冲导弹所能到达的极限位置也基本相同，可达域差别不大。由此可以看出，落角约束对可达域的影响不大，可根据飞行任务需求适当对终端弹道倾角约束进行调整，以达到更好的打击效果。

4结论

1)针对多脉冲导弹可达域的特点，引入加权的纵程和横程的组合性能指标函数，将可达域优化问题转化为最优控制问题；

2)建立多阶段、多约束的弹道优化模型，引入连接点约束条件处理各阶段不连续问题，并利用hp自适应伪谱法对优化问题进行求解，仿真结果验证了优化模型和优化方法的正确性，所得可达域也能很好地满足约束条件；

3)多脉冲导弹最佳可达区域的纵向跨度约为300 km，横向跨度可达到370 km；

4)多脉冲导弹发动机参数对可达域的影响规律如下：Ⅰ，Ⅱ脉冲发动机的装药比越大，推力比越小，时间间隔越小，可达域面积越大；

5)多脉冲导弹可达域的大小随终端速度的增加而减小，终端倾角对可达域的影响较小。

参考文献(References)

[1]Naumann K W， Stadler L J． Double-pulse solid rocket motor technology-applications and technical solutions[C]//Proceedings of 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2010:2345-2353.

[2]王志健，何永强，魏祥庚，等．空空导弹多脉冲固体火箭发动机能量分配优化研究[J]．弹箭制导与控制学报，2010，30(6)：144-146．

WANG Zhijian, HE Yongqiang, WEI Xianggeng, et al. An investigation of optimizing energy allocation on multi-pulse solid rocket motor in airborne missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(6): 144-146．(in Chinese)

[3]Lu P,Xue S B. Rapid generation of accurate entry landing footprints[J] Journal of Guidance, Control, and Dynamic, 2010, 33(3):756-767．

[4]Fahroo F, Doman D B, Ngo A D. Modeling issues in footprint generation for reusable launch vehicle[C]//Proceedings of IEEE Aerospace Conference, 2003: 1-9．

[5]Lu P, Xue S B. Rapid generation of accurate entry landing footprint[R]. AIAA 2009-5772，2009．

[6]雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙: 国防科学技术大学，2008．

YONG Enmi． Study on trajectory optimization and guidance approach for hypersonic glide-reentry vehicle[D]． Changsha: National University of Defense Technology，2008．(in Chinese)

[7]Amitabh Saraf， Leavitt A J， Mease K D．Landing footprint computation for entry vehicles[D]．Rhode Island: Guidance，Navigation，and Control Conference and Exhibit，AIAA 2004-4774, 2004．

[8]胡正东, 唐雪梅. 天基对地打击武器轨道规划与制导技术[M]．北京：国防工业出版社， 2013．

HU Zhengdong, TANG Xuemei. Trajectory planning and guidance technology for the space-based strike weapon[M]. Beijing: National Defense Industry Press, 2013．(in Chinese)

[9]冯必鸣, 聂万胜, 李柯. 再入飞行器可达区域近似算法及地面覆盖研究[J]．航天控制， 2012, 30(6): 43-49.

FENG Biming, NIE Wansheng, LI Ke. Research on closest-approach of footprint and coverage for reentry vehicle[J]. Aerospace Control, 2012, 30(6): 43-49. (in Chinese)

[10]钱杏芳，林瑞雄，赵亚男．导弹飞行力学[M]．北京：北京理工大学出版社，2000．

QIAN Xingfang, LIN Ruixiong, ZHAO Yanan. Flight dynamics of missiles[M]. Beijing: Beijing Institute of Technology Press, 2000．(in Chinese)

[11]Fahroo F,Ross I M．Costate estimation by a Legendre pseudospectral method[J]．Journal of Guidance，Control, and Dynamic, 2001, 24(2): 270-277.

[12]丁洪波, 蔡洪, 张士峰，等. 高超声速滑翔式再入飞行器最大航程飞行轨迹分析[J]．国防科技大学学报，2009, 31(6): 67-72.

DING Hongbo, CAI Hong, ZHANG Shifeng, et al. The maximum-range trajectory analysis of hypersonic glide-reentry vehicle[J]. Journal of National University of Defense Technology, 2009, 31(6): 67-72. (in Chinese)

[13]Darby C L，Hager W W，Rao A V,et al． Direct trajectory optimization using a variable low-order adaptive pseudo-spectral method[J]. Journal of Spacecraft and Rockets，2011，48(3)：433-445.

[14]Wachter A， Biegler L T． On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J]. Mathematical Programming，2006，106(1)：25-57.

Design and analysis of footprint optimization method for multiple-pulse missile

MINGChao1，SUNRuisheng1，LIANGZhuo2，BAIHongyang1

(1.College of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2.China Academy of Launch Vehicle Technology, Beijing 100076, China)

Abstract：In order to formulate tactical indicators and mission plan，the footprint for multiple-pulse missile was investigated. The footprint optimization problem can be transformed into an optimal control problem by introducing the cost function which is formulated as a weighted combination of down-range and cross-range. A multiple constraints and phases trajectory optimization model of double optimization design variables that are composed by the angle of attack and slip angle was established，and using the hp-adaptive pseudo-spectral method to solve it. Moreover, the effects of multiple-pulse motor parameters and terminal constraints on the footprint were emphatically analyzed. Simulation results show the efficiency of the proposed method in solving the footprint optimization design problem with multiple constraints and phases. The smaller interval time of multiple-pulse missile motor，the greater of thrust radio and the smaller mass radio of the pulse motor are corresponded to a bigger footprint. Compared with the terminal velocity, the impact angle affects the footprint to a lesser degree．

Key words：multiple-pulse missile； footprint optimization； hp-adaptive pseudospectral method； motor parameters； terminal constraints

中图分类号：TJ761.6;V412.4

文献标志码：A

文章编号：1001-2486(2016)01-143-07

作者简介：明超(1989—)，男，辽宁朝阳人，博士研究生，E-mail：nust802mc@126.com；孙瑞胜(通信作者)，男，副教授，博士，博士生导师，E-mail：srscom@163.com

基金项目：国家自然科学基金资助项目(11176012);江苏省普通高校研究生科研穿心计划工程资助项目(KYLX150394);总装预研基金资助项目(9140A31010114JB25465)

*收稿日期：2015-01-23

doi:10.11887/j.cn.201601023

http://journal.nudt.edu.cn