相依网络研究综述*

老松杨，王竣德，白　亮

(国防科技大学 信息系统工程重点实验室， 湖南 长沙　410073)



相依网络研究综述*

老松杨，王竣德，白亮

(国防科技大学 信息系统工程重点实验室， 湖南 长沙410073)

摘要：网络相依性和相依网络研究已经成为近年来复杂网络领域的热点，但是目前对相关研究进展进行综合归纳的文献却不多见。在对国内外相关文献进行系统分析的基础上，简要介绍相依网络研究涉及的渗流理论；描述该类型网络的级联失效过程；从相依网络的子网络特性、相依边的方向和类型、子网络组合方式等三个角度对相依网络鲁棒性的研究成果进行总结；并从理论和应用两方面对未来相依网络研究的发展方向进行展望。

关键词：相依网络；级联失效；渗流理论；鲁棒性;综述

经过几十年的发展，复杂网络研究的理论体系已经被逐步建立和完善，但这些理论仍然存在一定的局限性。因为以往对复杂网络的研究大多建立在孤立网络的基础之上，而在现实世界中每个网络都或多或少地与其他网络之间存在着各种各样的关联，例如物理依附、逻辑依赖、能量或信息交换等，严格意义上的孤立网络其实是不存在的。图1描述了电力、供水、交通运输、通信等基础设施之间的这种联系[1]。一旦某个网络中节点发生故障，网络间的联系会将故障的影响传播和放大，并可能影响其他网络的功能，最终一个很小的故障就有可能对整个系统造成灾难性后果[2]。这方面的典型案例就是2003年9月23日意大利大停电事故。

图1　网络化基础设施之间的联系Fig.1　Connections between network infrastructures

整个事件的起因就是电网中某个节点由于故障而失效，导致与其相连的计算机控制节点断电，而电网节点向计算机控制节点供电的同时，计算机控制节点也为电力节点提供控制信号。故障发生后因控制网络无法对电力网络进行有效调控而使得更多电力节点与电网脱离，最终诱发了全国规模的停电。产生这种现象的根源就是网络间存在的相依性，具有这种特性的网络就是相依网络(interdependent networks)。

相依网络有很多不同于孤立网络的性质。在相依网络中，节点之间存在的相依性使得故障可以跨网络传播，导致级联失效过程通常比单个网络更加剧烈，使得相依网络系统的鲁棒性较差。再比如在单个网络中，逐渐移除节点时的渗流过程通常表现为二阶形式，也就是说孤立网络的连通性是逐渐降低的；而在相依网络中，逐渐移除系统中的节点达到一定比例时会使得系统的连通性发生急剧变化，在时序曲线上表现为一阶形式。这些特性都意味着现实世界中相依的网络化基础设施在节点发生故障时面临的风险更高。因此研究相依网络的这些性质对于设计更加健壮的网络化系统、提高网络化基础设施抵御风险的能力有重要意义。

1主题

2010年，Buldyrev[3]等在Nature上发表了研究相依网络级联失效过程的文章，提出了全相依的相依网络模型，即两个网络的节点之间存在一一对应的相依关联，这种情况下当一个网络中的节点失效后另一个网络中与其相依的节点也会失效。相依网络的级联失效过程如图2所示。

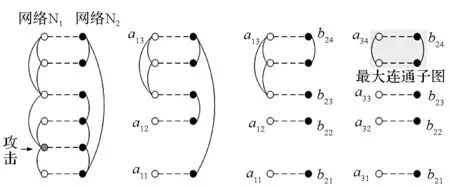
(a) 初态(a) Initial state (b) 第一阶段(b) Stage 1 (c) 初态(c) Stage 2　(d) 第二阶段(d) Steady state图2　相依网络的级联失效过程[3]Fig.2　Cascading failure of interdependent networks

在该模型中，作者假定节点只有处于最大连通子图(giant component)中才能维持正常功能。若网络N1中的一个节点被攻击而失效，则N1中所有与之相连的连边均被移除，此时N1被分成3个子图(如图2(b)所示)。根据假设，N1的非最大连通子图的节点也失效；由于节点间相依关系的存在，N1中节点失效将导致网络N2中相应节点失效，进而使N2分成4个子图(如图2(c)所示)，N2中非最大连通子团的节点也失效；反过来，N2中失效节点又引起N1中对应的相依节点失效，如此反复迭代至稳态[4]。以上过程就是相依网络的级联失效。此外，还利用渗流理论研究了相依网络的渗流过程从二阶相变转变为一阶相变的现象，也就是说随着失效节点的比例达到某一阈值时，相依网络的连通性会急剧下降。

这篇文章引领了相依网络研究的热潮(如图3、图4所示)，此后研究人员分别从相依网络的子网类型、相依强度、相依类型等角度研究了其鲁棒性问题，并对不同攻击方式下相依网络联通性进行了分析，取得了丰硕成果，建立了相对完善的相依网络理论体系[5]。文献[6]从理论体系、已有模型和应用范围等方面对这些成果进行了比较全面的总结。

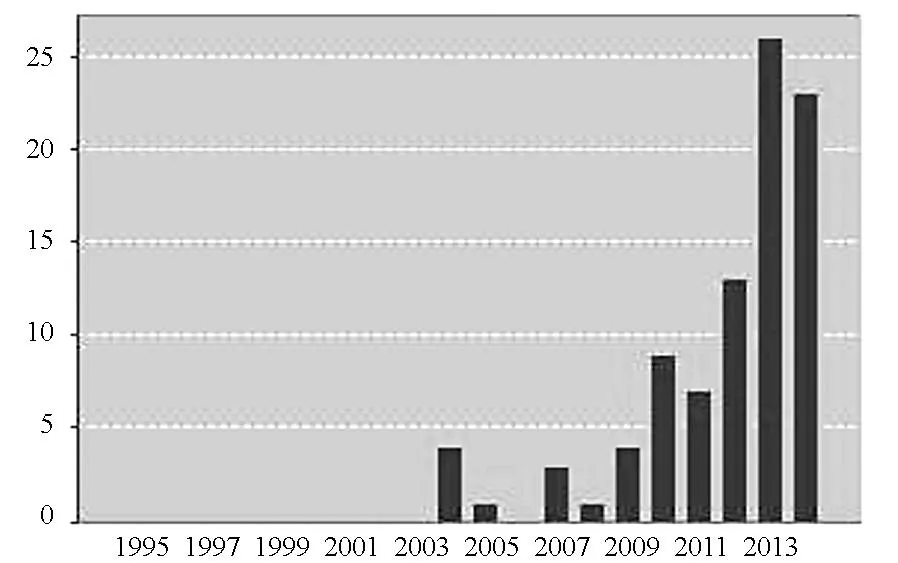
图3　每年出版的相依网络方面的文献数Fig.3　Published items of interdependent networks in each year

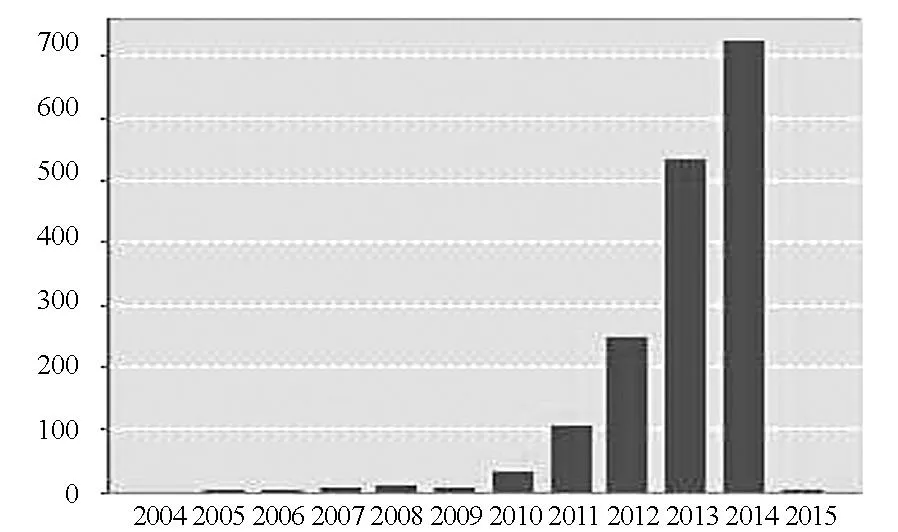
图4　每年相依网络方面的引文数Fig.4　Citations of interdependent networks in each year注：以上结果是在web of science中以interdependent networks作为关键词对文献标题进行查询得到(截至2015年1月)。

近年来相依网络鲁棒性研究的一般思路是利用渗流理论，结合仿真分析或数学推导(如利用迭代函数研究级联失效、利用矩阵分析方法研究网络连通性[7]等)的方法研究相依网络在随机或蓄意攻击下的鲁棒性问题[8]。

相依网络有三个要素：组成相依网络的子网络、子网络间的相依连边及子网络的组合方式，现有的相依网络研究也多是从这几个方面展开的。因此接下来在介绍相关理论的基础上从上述角度对相关研究作以下综述。

1.1相关理论

渗流理论(percolation theory)是目前研究相依网络的常用方法，最初用来描述流体在随机介质中运动特性[9]。在复杂网络方面，该理论最早被用来研究无限大二维正方形网格的连通性问题：以概率p随机地占据网格上的点，当两个被占据的点相邻时称其是连通的。连通点的集合称为连通子图。当p较小时，网格上只会存在一些孤立子图；但当p超过某一数值时，各个孤立子图则会形成连通的极大子图，相应的数值就是渗流阈值Pc。以上过程反过来看，就成了在一个网络中移除一定比例的节点后分析网络的连通性、进而研究网络鲁棒性的问题。随机移除网络中比例为1-p的节点(即每个节点被移除的概率为1-p)，当移除比例大于渗流阈值Pc时，网络中的极大连通子图存在的概率为P∞最终降为0。渗流过程中还伴随着渗流相变现象，渗流相变可分为二阶相变、一阶相变。在时序曲线上二级相变一般为连续曲线，而一级相变为不连续曲线，即在临界值处会发生跳跃突变的现象，如图5所示。

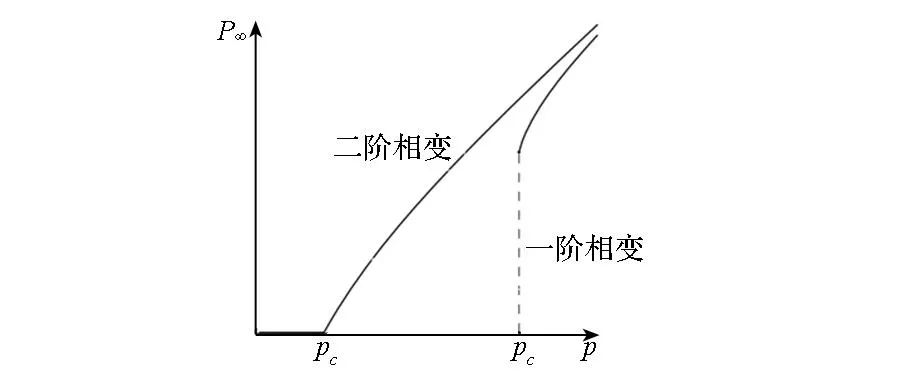
图5　一阶和二阶渗流相变示意图[10] Fig.5　Schematic demonstration of first and second order percolation transitions

1.2相依网络的子网络

子网对相依网络鲁棒性的影响主要通过子网络类型及节点数、平均度等特性得以体现。

组成相依网络的子网络类型有很多种：ER(Erdos-Renyi)网络、RR(Random Regular)网络、SF(Scale Free)网络、BA(Barabási-Albert)网络、WS(Watts-Strogatz)网络等。这些网络作为子网组成的相依网络的鲁棒性表现不尽相同。现有研究表明，在除子网类型外的其他条件相同时，RR-RR相依网络的鲁棒性比ER-ER相依网络好[11]，ER-ER相依网络比SF-SF相依系统鲁棒性好[12-13]。这几种相依网络的鲁棒性可以归纳为RR-RR>ER-ER>SF-ER>SF-SF。这是子网络中节点度分布决定的——只考虑节点度分布的影响时，子网络的度分布越均匀，其组成的相依网络的鲁棒性越好[14]。度分布越不均匀，鲁棒性越差。对于SF网络，当其度分布极不均匀时，由其构成的相依网络在单个节点失效时整个相依网络也可能完全崩溃[15]。

除了网络类型和度分布外，子网络的其他性质，如节点数、平均度[16]、网间相似性等对相依网络的鲁棒性也有一定的影响。

对于节点数量来说，子网络的节点数量越多，相依网络在渗流阈值Pc处的相变过程越剧烈。极限情况下，当子网络节点数量为无穷大时，该过程表现为一阶形式。此外子网络的平均度对相依系统的鲁棒性也有影响，平均度越高，鲁棒性越好。例如Hu[17]等发现在完全相依的ER网络中，随着平均度增大，相依网络的级联效应逐渐减弱。

网间相似性(inter-similarity)是指子网络内部节点度高的节点间倾向于产生相依关联。例如世界范围内的港口和机场网络组成的相依系统，重要的港口节点倾向于同重要的机场连接(这里相依关联是指地理位置相同)。Parshani[18]，Hu[17]等用仿真和解析方法研究了港口-机场组成的相依网络系统，发现两个网络的内部相似性越高，整个系统在面对随机失效时的鲁棒性就越好。该结论说明通过提高节点度较高节点间相依连边的可靠性(如添加冗余)可以有效提高系统的鲁棒性，这种特性可以指导设计更健壮的网络化系统。

1.3相依网络的相依边

相依边的物理意义是子网络之间的物质能量信息交换等关联关系。相依边是相依网络存在的基础，也是影响相依网络鲁棒性最直接的因素。相依边主要通过其方向、类型及比例等属性影响整个相依网络的鲁棒性。

1.3.1相依边方向

根据实际网络之间节点的依赖关系可以把相依网络模型中的相依连边分为有向和无向两种。Fu[13]等研究了有向相依系统和无向相依系统的渗流过程，证明了当其他条件相同时，相依连边有向的相依网络鲁棒性比相依连边无向的相依网络差。

造成这种现象的原因是有向系统中更有可能产生更长的相依链(dependency chains)。相依链是指在两个子网A，B组成的相依模型中，A中节点u支持B中节点v，v反过来又支持A中节点w(w≠u)，如此往复形成的相依节点集。相依链上节点的故障会通过相依链在子网之间传播，还有可能扩散到与相依链相连的其他节点中，引起故障的级联，降低系统的鲁棒性。有向系统中的相依链往往比无向系统中更长，从而使得故障在网络间更加有效地传播，因此有向相依网络的鲁棒性较差。

1.3.2相依边类型

相依边类型有连接边(connectivity links)、依赖边(dependency links)两种。连接边的作用是连接不同网络的节点，使得相依网络的子网络能够协同工作；依赖边表示某个节点的功能依赖于其他节点。据此可以把相依网络分为三类：子网络间只存在依赖边的相依网络；子网络间只存在连接边的相依网络；子网络间同时存在依赖边和连接边的相依网络。

1)只存在依赖边。Buldyrev[3]等研究了网络间只存在无向依赖边且节点之间具有一一对应关系的情形；Bashan Amir[19]等用解析方法分析了依赖边的分布对网络鲁棒性的影响；Shao[20]等认为实际网络中节点的对应关系不是一一对应的，而是一对多或多对多的。基于此提出了具有多重依赖关系的相依网络模型并研究了该类相依网络的渗流过程，最后得出结论：当相依网络的子网络之间依赖边的平均度很大时，该相依网络模型的渗流特性与单个ER网络类似。

2)只存在连接边。2010年，Leicht[21]等研究了网络间只存在连接边的相依网络的渗流理论，结果显示，这种情况下增加子网络间的连边可以有效降低渗流阈值，提高网络的鲁棒性。这与只存在依赖边的网络的性质刚好相反。

3)同时存在依赖边和连接边。Hu[22]和Zhou[23]等利用渗流理论研究了同时包含依赖边和连接边两种类型的相依网络的性质，观察到了一阶、二阶混合相变的渗流相变现象。Amir Bashan[11]等研究了两个平均度都为k、规模为s的ER网络组成，且两个ER网络之间同时包含依赖边和连接边的相依网络。在移除比例为1-p的节点后，该相依网络依然存在最大连通子图的概率可表示为：

P∞=ps-1[1-exp(-kpP∞)]s

(1)

1.3.3相依边比例

相依边比例表征相依网络中具有相依关系的节点对的数量，可以用相依网络之间的相依强度进行度量。

相依网络的相依强度q指的是相依网络中有相依关系的节点所占的比例：q=0对应于网络之间无相依关系，q=1表示子网络间完全相依，即节点之间具有一一对应的相依关系。Parshani和Zhang等通过研究指出，当网络之间的连接强度从0到1逐渐增加时，相依网络的渗流相变过程会由连续的二阶相变演化为跳变的一阶相变[24-25]。比如对于RR网络组成的相依网络，当网络之间的相依强度较小时，相依网络的渗流过程表现为平滑的二阶相变，但随着相依强度增大则逐渐演变为一阶相变。

Zhou[26]等对两个SF网络组成的相依网络进行研究发现，这种相依网络的相依强度q存在两个临界值q1和q2(q1

1.4相依网络的组合方式

在早期开展研究中，研究人员大多从比较简单的模型入手，通过研究由两个子网络构成的相依网络模型的渗流特性和鲁棒性特点。随着研究的深入，有学者从子网络规模和组合方式的角度对相依网络模型进行了拓展，目前这方面的一个研究重点就是网络组成的网络——多层网络(Network Of Networks，NON)的鲁棒性。

图6　相依网络的组合方式Fig.6　Combination modes of interdependent networks

目前研究较多的是由ER，RR等网络作为子网络，以链形、星形、树形或环形组合方式组成的NON的性质，如图6所示。图中每个节点表示一个子网络，边表示子网络之间的相依关联，这里相依边可以是有向也可以是无向的[27-28]。

1.4.1链形、星形

对于链形、星形组合方式组成的相依网络，利用渗流理论研究其鲁棒性可以得到结论：在这两种组合方式下，相依网络的渗流阈值和极大连通子图规模相同，并且极大子图存在的概率可以表示为：

P∞=p[1-exp(-kP∞)]n

(2)

对于ER网络组成的星形NON，存在一个相依强度的临界值——当相依强度大于这个临界值时NON的渗流过程为一阶相变，反之则为平滑的二阶相变状态[29-31]，并且级联失效后存在最大连通子图的概率取决于星形网络的拓扑结构。

1.4.2树形

根据子网络的不同类型，Gao[32]等研究了由RR和ER网络组成的两种树形NON的渗流特性。对于n个平均度为k的ER网络组成的NON，移除一定比例节点后存在极大连通子图的概率为：

P∞=p[1-exp(-kP∞)]n

(3)

而对于由n个平均度都为k的相依RR网络组成的树形NON，移除比例为1-p的节点后，存在最大连通子图的概率为：

(4)

在极限情况即子网络个数n=1时，树形NON在pc处的渗流过程为二阶形式，而n>1时则为一阶相变。此外在相同条件下，RR网络组成的树形NON鲁棒性比ER网络组成的树形NON更好，并且在ER型NON中关于子网络平均度k存在临界阈值kmin(n) (与子网络个数n有关)。当子网络平均度小于此阈值时，即使只有一个节点失效也会导致整个NON的崩溃。但由RR网络构成的树形NON不存在这样的阈值。

1.4.3环形

对于图6(d)所示的环形NON：由n个平均度都为k的ER网络组成，各个子网具有相依关系的节点比例q都相同，且相依边的方向也一致。当对每一个子网络中的节点都移除同样比例1-p的节点时，可以得到最大连通子图的概率满足：

P∞=p[1-exp(-kP∞)](qP∞-q+1)

(5)

1.4.4其他组合方式

除以上方式外，对于其他组合方式也有人做了一些探索，Buldyrev[33]等研究了由ER子网络组成的RR型相依网络——由n个ER网络组成，每个子网都依赖于其他m个子网的鲁棒性和渗流特性。与环形组合方式分析过程类似，假定每个子网初始失效节点的比例都为1-p，子网间具有相依关系的节点比例q都相同，则这类相依网络级联失效后的极大连通子图与子图的个数无关，可表示为：

(6)

对比式(2)～(6)可知：链形、星形和树形NON在级联失效后最大连通子图的存在概率与子网个数有关，并且在节点失效比例等初始条件相同的情况下，网络的渗流阈值和级联失效后存在极大子图的概率也相同。但环形以及RR型NON级联失效后的最大连通子图存在的概率与子网个数无关[27]。

2结论

在网络化基础设施相依关联逐渐加强的背景下，从相依网络的概念被提出到现在，研究人员逐步分析了不同子网类型、不同相依方式及强度[34]、不同攻击方式下相依网络的特性。近两年又对不同子网类型、不同组合方式、不同耦合强度等条件下网络相依性对NON鲁棒性的影响进行了探讨。在应用范围上，相依网络研究已经逐渐从最初的网络化基础设施设计和优化[35]、安全操作和控制[36-38]等方面，拓展到了如生理系统、生态学、流行病传播[39]、气候变化、信息扩散[40]、经济网络、交通网络等其他很多方面，为人们理解社会、自然的内在运行规律提供了一种理论手段。

综上所述，我们可以对今后该领域研究的大致方向进行预测，具体可以概括为以下两方面：

1)理论方面。节点或边上加上权值以表示节点或边的容量、负载、失效概率等物理含义的加权相依网络鲁棒性分析仍是目前该领域研究的一个薄弱环节[41-43]。另外现有研究模型的规模多是固定的，而现实世界中网络大都处于动态演化的状态，因此考虑节点或边演化的动态相依网络性质也应该给予足够的重视[44]。其他如孤立网络的各种动力学行为在相依网络中的表现、节点的空间约束对相依系统的影响等也是今后该领域研究的潜在热点[45]。

2)实践应用方面。目前所建的相依网络模型对实际系统的描述能力有限。以往开展的相依网络研究大都从理论角度出发，没有把目光集中于实际相依网络的分析建模上，所建模型与现实世界中的系统没有紧密联系。因此，从现实出发、根据实际系统的特点和数据进行相依网络分析应该成为今后的研究重点。此外，网络相依性理论在如社会学、经济学、生态学、生理系统等新领域的应用也应成为下一步关注的重点。

参考文献(References)

[1]Gao J X, Li D Q, Havlin S. From a single network to a network of networks[J]. National Science Review, 2014, 1(3): 346-356.

[2]Rinaldi S M, Peerenboom J P, Kelly T K. Identifying, understanding, and analyzing critical infrastructure interdependencies[J]. Control Systems, IEEE, 2001, 21(6): 11-25.

[3]Buldyrev S V, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028.

[4]李国颖,成柏松,张鹏,等. 相互依存网络鲁棒性研究综述[J]. 电子科技大学学报, 2013, 42(1):23-28.

LI Guoying, Cheng Baisong, Zhang Peng, et al. Review of the interdependent networks[J]. Journal of University of Electron ic Science and Technology of China, 2013, 42(1):23-28. (in Chinese)

[5]Danziger M M, Bashan A, Berezin Y, et al. An introduction to interdependent networks[C]//Proceedings of the 22nd International Conference on Nonlinear Dynamics of Electronic Systems, 2014, 438: 189-202.

[6]D′Agostino G, Scala A. Networks of networks: the last frontier of complexity[M]. Germany: Springer, 2014.

[7]Martín-Hernández J, Wang H, Van Mieghem P, et al. Algebraic connectivity of interdependent networks [J]. Physica A: Statistical Mechanics and its Applications, 2014, 404: 92-105.

[8]刘润然, 贾春晓, 章剑林, 等. 相依网络在不同攻击策略下的鲁棒性[J],上海理工大学学报, 2012, 34(3): 235-239.

LIU Runran, JIA Chunxiao, ZHANG Jianlin, et al. Robustness of interdependent networks under several intentional attack strategies[J]. Journal of University of Shanghai for Science and Technology, 2012, 34(3): 235-239. (in Chinese)

[9]董高高. 遭受攻击的耦合相依网络的鲁棒性研究[D]. 镇江：江苏大学, 2013.

DONG Gaogao. Study on robustness of coupled interdependent networks under attacks[D]. Zhenjiang:Jiangsu University, 2013. (in Chinese)

[10]Gao J X, Buldyrev S V, Stanley H E, et al. Networks formed from interdependent networks[J]. Nature Physics, 2011, 8(1): 40-48.

[11]Bashan A, Havlin S. The combined effect of connectivity and dependency links on percolation of networks[J]. Journal of Statistical Physics, 2011, 145(3): 686-695.

[12]Zhang Q, Li D, Kang R, et al. Reliability analysis of interdependent networks using percolation theory[C]//Proceedings of International Conference on Signal-Image Technology & Internet Based Systems, 2013:626-629.

[13]Fu G H, Dawson R, Khoury M, et al. Interdependent networks: vulnerability analysis and strategies to limit cascading failure[J]. The European Physical Journal B, 2014, 87(7): 148.

[14]Buldyrev S V, Shere N W, Cwilich G A. Interdependent networks with identical degrees of mutually dependent nodes[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 83(1):1-8.

[15]Zhang P, Cheng B S, Zhao Z, et al. The robustness of interdependent transportation networks under targeted attack[J]. Europhysics Letters, 2013, 103(6):68005.

[16]Cheng Z S, Cao J D, Hayat T. Cascade of failures in interdependent networks with different average degree[J]. International Journal of Modern Physic C, 2014, 25(5):1440006.

[17]Hu Y, Zhou D, Zhang R, et al. Percolation of interdependent networks with inter-similarity[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 88(5): 052805.

[18]Parshani R, Rozenblat C, Ietri D, et al. Inter-similarity between coupled networks[J]. Europhysics Letters, 2010, 92(6): 68002.

[19]Bashan A, Parshani R, Havlin S. Percolation in networks composed of connectivity and dependency links[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 83(5): 051127.

[20]Shao J, Buldyrev S V, Havlin S, et al. Cascade of failures in coupled network systems with multiple support-dependence relations[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 83(3): 036116.

[21]Leicht E A, D′Souza R M. Percolation on interacting networks[J]. arXiv preprint arXiv:0907.0894, 2009.

[22]Hu Y, Ksherim B, Cohen R, et al. Percolation in interdependent and interconnected networks: Abrupt change from second-to first-order transitions[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2011, 84(6): 066116.

[23]Zhou D, Bashan A, Cohen R, et al. Simultaneous first-and second-order percolation transitions in interdependent networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2014, 90(1): 012803.

[24]Parshani R, Buldyrev S V, Havlin S. Interdependent networks: Reducing the coupling strength leads to a change from a first to second order percolation transition[J]. Physical Review Letters, 2010, 105(4): 048701.

[25]Zhang P, Cheng B S, Zhao Z, et al. The robustness of interdependent transportation networks under targeted attack[J]. Europhysics Letters, 2013, 103(6): 68005.

[26]Zhou D, Gao J, Stanley H E, et al. Percolation of partially interdependent scale-free networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 87(5): 052812.

[27]Gao J, Buldyrev S V, Havlin S, et al. Robustness of a network of networks[J]. Physical Review Letters, 2011, 107(19): 195701.

[28]Gao J, Buldyrev S V, Havlin S, et al. Robustness of a network formed by n interdependent networks with a one-to-one correspondence of dependent nodes[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2012, 85(6): 066134.

[29]Dong G, Gao J, Du R, et al. Robustness of network of networks under targeted attack[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 87(5): 052804.

[30]Dong G, Tian L, Zhou D, et al. Robustness of n interdependent networks with partial support-dependence relationship[J]. Europhysics Letters, 2013, 102(6): 68004.

[31]Dong G, Tian L , Du R, et al. Robustness of network of networks with interdependent and interconnected links[J].Physica A: Statistical Mechanics and its Applications, 2013, 424:11-18.

[32]Gao J, Buldyrev S V, Havlin S, et al. Robustness of a tree-like network of interdependent networks[J]. arXiv preprint arXiv:1108.5515, 2011.

[33]Gao J, Buldyrev S, Stanley H E, et al. Percolation of a general network of networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 88(6): 062816.

[34]Zhou D, Stanley H E, D’Agostino G, et al. Assortativity decreases the robustness of interdependent networks[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2012, 86(6): 066103.

[35]Parandehgheibi M, Modiano E. Robustness of interdependent networks: the case of communication networks and the power grid[C]//Proceedings of IEEE Global Communications Conference, 2013:2164-2169 .

[36]Zio E, Sansavini G. Modeling interdependent network systems for identifying cascade-safe operating margins[J]. IEEE Transactions on Reliability, 2011, 60(1): 94-101.

[37]Rosato V, Bologna S, Meloni S, et al. Interdependency effects measured on complex interdependent networks[C]//Proceedings of Complexity in Engineering，2010: 27-32.

[38]Schneider C M, Yazdani N, Araújo N A M, et al. Towards designing robust coupled networks[J]. Scientific reports, 2013, 3:1969.

[39]Son S W, Bizhani G, Christensen C, et al. Percolation theory on interdependent networks based on epidemic spreading[J]. Europhysics Letters, 2012, 97(1): 16006.

[40]Shin D H, Qian D, Zhang J. Cascading effects in interdependent networks[J]. IEEE Network,2014,28(4):82-87.

[41]Qiu Y. The effect of clustering-based and degree-based weighting on robustness in symmetrically coupled heterogeneous interdependent networks[C] //Proceedings of IEEE International Conference on Systems, Man, and Cybernetics (SMC), 2013: 3984-3988.

[42]Qiu Y. Optimal weighting scheme and the role of coupling strength against load failures in degree-based weighted interdependent networks[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(8): 1920-1924.

[43]Qiu Y. Cascading dynamics with local weighted flow redistribution in interdependent networks[J]. The European Physical Journal B, 2013, 86(7): 1-9.

[44]Podobnik B, Horvatic D, Dickison M, et al. Preferential attachment in the interaction between dynamically generated interdependent networks[J]. Europhysics Letters, 2012, 100(5): 50004.

[45]Bashan A, Berezin Y, Buldyrev S V, et al. The extreme vulnerability of interdependent spatially embedded networks[J]. Nature Physics, 2013, 9(10): 667-672.

Review of the interdependent networks

LAOSongyang,WANGJunde,BAILiang

(Science and Technology on Information Systems Engineering Laboratory, National University of Defense Technology, Changsha 410073, China)

Abstract：In recent years, the network dependency and interdependent networks have become a research hotspot in the field of complex network, but literature about the overview of related research progress is still very rare. Based on the systematic research of domestic and overseas literatures, the percolation theory of the interdependent networks was briefly introduced, and the cascading failure process of the interdependent networks was described. Then the related progress was summarized from three aspects that can affect the robustness of interdependent networks: characteristics of sub network, type of dependency edge, the combination of sub networks. Finally, the future development direction of interdependent networks was prospected in both theoretical and practical aspects.

Key words：interdependent networks; cascading failures; percolation theory; robustness; overview

中图分类号：O231;O157.5

文献标志码：A

文章编号：1001-2486(2016)01-122-07

作者简介：老松杨(1968—)，男，广东佛山人，教授，博士，博士生导师，E-mail：laosongyang@vip.sina.com

基金项目：国家自然科学基金资助项目(60902094)

*收稿日期：2015-01-30

doi:10.11887/j.cn.201601020

http://journal.nudt.edu.cn