热障涂层厚度及其涂敷下材料内部缺陷的红外定量识别*

陈　林，杨　立，范春利，石宏臣，赵小龙

(1. 海军工程大学 动力工程学院， 湖北 武汉　430033； 2. 海军蚌埠士官学校， 安徽 蚌埠　233012)



热障涂层厚度及其涂敷下材料内部缺陷的红外定量识别*

陈林1,2，杨立1，范春利1，石宏臣1，赵小龙1

(1. 海军工程大学 动力工程学院， 湖北 武汉430033； 2. 海军蚌埠士官学校， 安徽 蚌埠233012)

摘要：针对热障涂层结构材料红外定量检测存在的不足，提出基于脉冲相位的LM(Levenberg-Marquardt)识别算法。针对研究问题，建立了轴对称圆柱坐标下热障涂层结构材料的瞬态导热模型，利用有限体积法计算出检测表面的温度场，经快速傅里叶变换得到检测表面的相位分布，分析待检测参数对检测表面相位差的影响。以相位为识别条件，采用LM反演算法对热障涂层厚度及其涂敷下材料内部缺陷位置大小进行定量识别，并采用数值实验方法验证了基于相位的LM识别方法的有效性。

关键词：热障涂层；红外检测；定量识别；脉冲相位

热障涂层(Thermal Barrier Coating，TBC)由于其良好的隔热和防腐蚀性能在航空航天等领域得到广泛的应用。常见的热障涂层结构材料由陶瓷层、黏结层和合金基体构成，为了保证热障涂层结构材料的耐高温性和抗腐蚀性，热障涂层结构材料都有其合理的涂层厚度，而材料的完好是机械或部件正常工作的基本要求，因此对热障涂层厚度及其涂敷下材料内部缺陷的检测具有重要的意义。与微波检测[1]、超声检测[2]等传统检测方法相比，红外无损检测法对热障涂层结构材料的检测具有检测面积大、速度快等优点。红外热像检测法主要有脉冲检测法[3]、锁相检测法[4]、脉冲相位检测法[5]等，其中脉冲相位检测法因兼具有脉冲检测法和锁相检测法的优点而在红外检测中得到广泛的应用。文献[6]采用脉冲红外热像法对涂层厚度检测进行了研究，文献[7]将脉冲红外热像法应用于涂层厚度及其失效过程的监测，文献[8-9] 对涂层结构板材内部缺陷的脉冲相位红外热成像法进行了研究。然而现有文献对相位检测的定量化研究都是通过热传导机理来进行，由于受复杂边界条件的影响，在实际传热模型的求解时，多数情况下被检测参数对检测表面相位分布的影响都不能得到精确的解析解，因而为了得到被检测参数的定量化结果，大都是在一维简化模型下进行研究，这样往往带来检测结果与实际情况存在较大的偏差。而依据导热反问题理论来求解被检测参数的方法能很好地满足定量化检测的要求，因此将反问题算法与红外检测技术相结合对于红外检测技术从定性到定量的转变具有重要的意义。

目前导热反问题优化算法主要有共轭梯度法[10]、数值搜索算法[11]、遗传算法[12]等，其中，LM(Levenberg-Marquardt)因求解方法简单、收敛速度快等优点在反问题求解方面得到较广的应用[13-14]。本文主要通过将反问题算法与脉冲相位检测技术相结合来研究热障涂层厚度及其涂敷下材料内部缺陷的定量识别。

1红外检测正问题模型

在轴对称柱坐标系下，三维导热问题可以简化为二维导热问题来研究，这样将大大节省计算时间，因而本文研究问题为轴对称圆柱坐标下的热障涂层结构材料的红外无损检测，如图1所示。研究模型的半径Lr=20 mm，Ly3为陶瓷层厚度，Ld为黏结层的厚度，在一般的热障涂层结构材料中黏结层的典型厚度为Ld=0.1 mm[15]，基体的厚度Ls=2 mm，在合金基体中有圆弧状的内部缺陷，缺陷内充满空气，Lr1为缺陷距圆柱体中心的距离，Lr2为缺陷距圆柱体外边界的距离，Ly1为缺陷距非加热面的距离，Ly2为缺陷距加热面的距离，参数Lr1，Lr2，Ly1和Ly2决定缺陷的位置和大小。为简化分析，模型外侧面r=Lr处视为绝热，非加热面考虑为绝热化处理，也视为绝热，假设材料是均质的，各向同性，则可建立如下的传热方程：

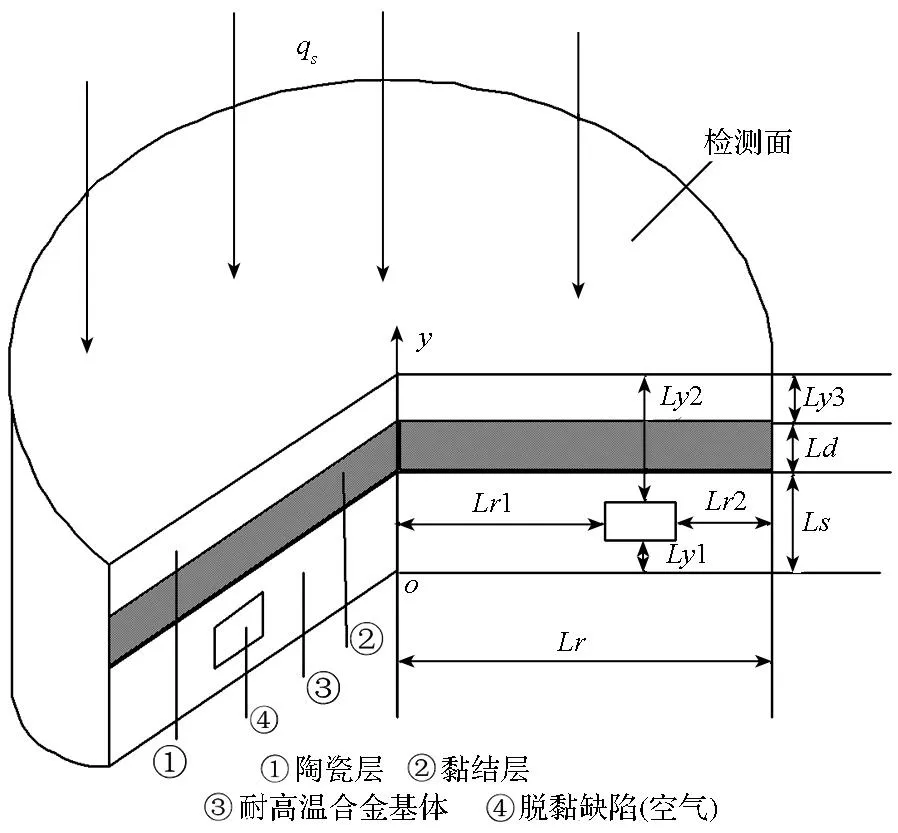
图1　热障涂层结构材料红外无损检测模型Fig.1　Nondestructive testing model of thermal barrier coating structures by infrared technology

(1)

初始条件：

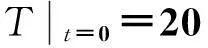
(2)

边界条件：

(3)

(4)

(5)

其中：T为温度，℃；k为导热系数，W/(m·℃)；ρ为密度，kg/m3；c为比热容，J/(kg·℃)(各材料的物性参数如表1所示)；Tf=20 ℃为环境温度；αq=0.9为检测表面的热量吸收系数；α=10 W/(m2·℃)为检测表面与环境的换热系数；在t=0～0.1 s时，热流强度qs=106W/m2，在t>0.1 s 时，qs=0。

表1　不同材料的物性参数

2反演识别方法

热障涂层厚度及其涂敷下材料内部缺陷的反演识别可描述为：依据检测表面的相位来识别热障涂层厚度及材料内部缺陷的位置大小。在反问题求解时，式(1)～(5)中除了参数Lr1，Lr2，Ly1，Ly2，Ly3为未知量外，其他参数均为已知。检测表面的温度通过红外热像仪测得，检测表面的相位通过对温度进行快速傅里叶变换(Fast Fourier Transform, FFT)得到。

2.1Levenberg-Marquardt反演识别算法

反演优化算法通常是对目标函数S(P) 进行最小化求解：

(6)

式中，P=(p1,p2,…,pn)是待识别的参数向量，对于本文热障涂层厚度及材料内部缺陷位置大小的定量识别P=(Lr1,Lr2,Ly1,Ly2,Ly3)，Yi为实际检测时得到的相位值，Φi为在参数向量P下通过式(1)～(5)计算得到的相位值，m为检测表面的离散点数。由于在“峰值”频率(检测表面相位差最大时对应的频率)下缺陷的可检测性最好，因而在反演识别时，只选取“峰值”频率下检测表面的离散相位值作为识别输入参数。

从偏差原理出发，当目标函数S(P)满足如式(7)所示收敛准则时，可以停止迭代求解并认为得到最终的识别结果。

S(P)<ε

(7)

式中，ε为一个给定的极小的正数。

为了使目标函数S(P)达到最小化，将目标函数S(P)对每个识别参数进行偏微分求导，并令每一个偏导数等于零，即：

(8)

将Φi通过泰勒级数展开并略去高阶项，再将一个调节系数μk添加到计算结果中去，从而得到LM算法的迭代公式为：

(9)

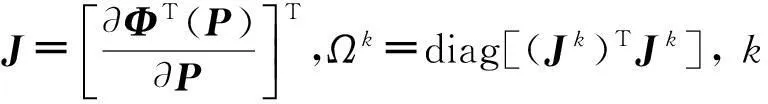
2.2迭代求解过程

1)给定一个热障涂层厚度及材料内部缺陷位置大小的初始假设P0，将P0作为开始迭代计算的输入条件。

2)在参数向量Pk+1下求解方程式(1)～(5)得到检测表面各测温点的温度，对检测表面测温点温度进行FFT变换，得到测量点处相位Φ(Pk)(k=0,1,2,…)。

3)在参数向量Pk下求解目标函数S(Pk)，并依据收敛标准式(7)判断其是否满足收敛条件，如果满足收敛条件则停止迭代，将其作为最终定量识别结果，否则依据式(9)对参数Pk进行修正得到下次的识别参数Pk+1，并返回步骤2。

3检测表面的相位差分布规律

为了获得检测表面的相位分布，利用有限体积法对建立的模型进行脉冲激励下温度场的模拟计算，对模拟计算得到的温度进行FFT变换，得到缺陷对应检测表面和非缺陷对应检测表面温度变化的相位信息，采样窗口时间为10 s，采样频率为10 Hz。材料内部缺陷位置大小参数Lr1=12 mm，Lr2=6 mm，Ly1=15 mm，Ly2=0.6 mm，陶瓷层厚度参数Ly3=0.3 mm，下文的分析都是在变化其中某一参数值而保持其他参数值不变下进行的。

3.1参数Ly1对检测表面相位差的影响

材料内部缺陷位置大小参数Ly1分别取为1.3 mm，1.4 mm，1.5 mm，缺陷(缺陷中心)对应检测表面与非缺陷(圆柱中心)对应检测表面的相位差分布如图2所示，由图可知，随着参数Ly1值的增大，检测表面的相位差最大值(指绝对值)减小，但是检测表面相位差的改变量较小，可见参数Ly1对检测表面相位分布的影响较小。

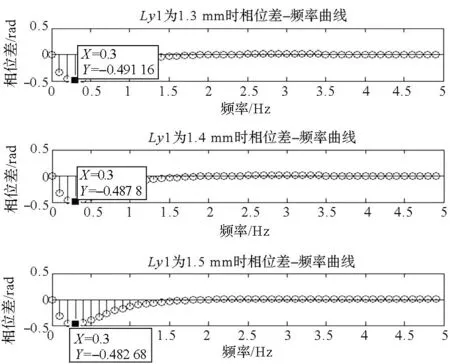
图2　参数Ly1对检测表面相位差的影响Fig.2　Impact of parameter Ly1 on the phase difference

3.2参数Ly2对检测表面相位差的影响

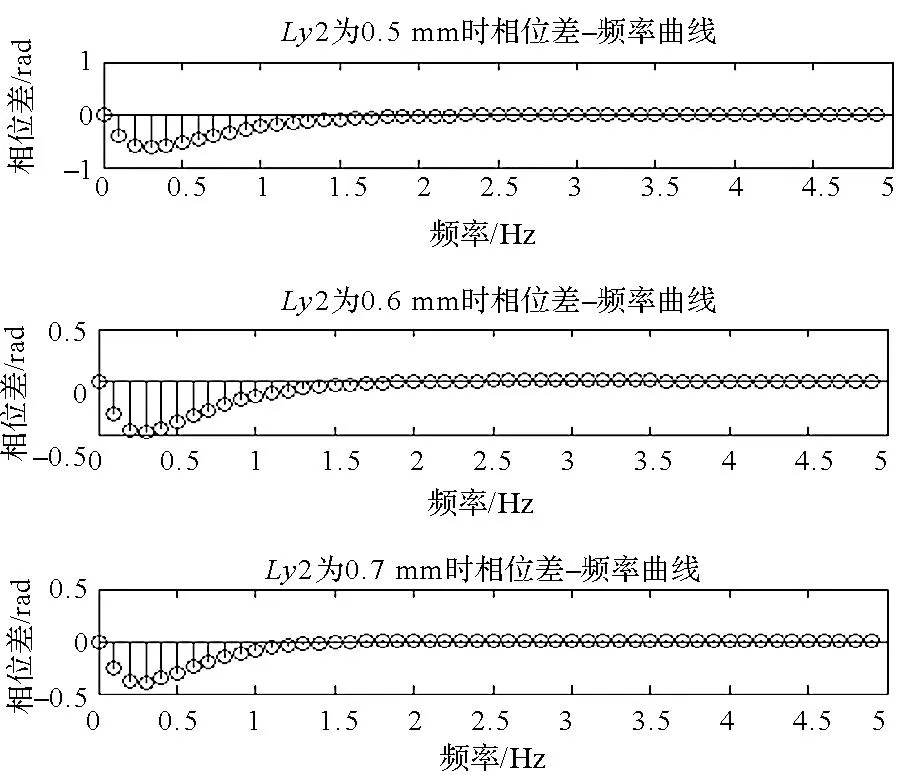
图3　参数Ly2对检测表面相位差的影响Fig.3　Impact of parameter Ly2 on the phase difference

材料内部缺陷位置大小参数Ly2分别取为0.5 mm，0.6 mm，0.7 mm，缺陷(缺陷中心)对应检测表面与非缺陷(圆柱中心)对应检测表面的相位差分布如图3所示，由图可知，与参数Ly1相同，检测表面的相位差最大值(指绝对值)随着参数Ly2值的增大而减小，并且检测表面相位差的改变量相对较大，可见参数Ly2对检测表面相位分布的影响较大。

3.3参数Ly3对检测表面相位差的影响

陶瓷层厚度参数Ly3分别取为0.2 mm，0.3 mm，0.4 mm，缺陷(缺陷中心)对应检测表面与非缺陷(圆柱中心)对应检测表面的相位差分布如图4所示，由图可知，随着参数Ly3值的增大，检测表面的相位差最大值(指绝对值)增大，检测表面相位差的改变量相对较大，其对检测表面相位分布的影响较大。

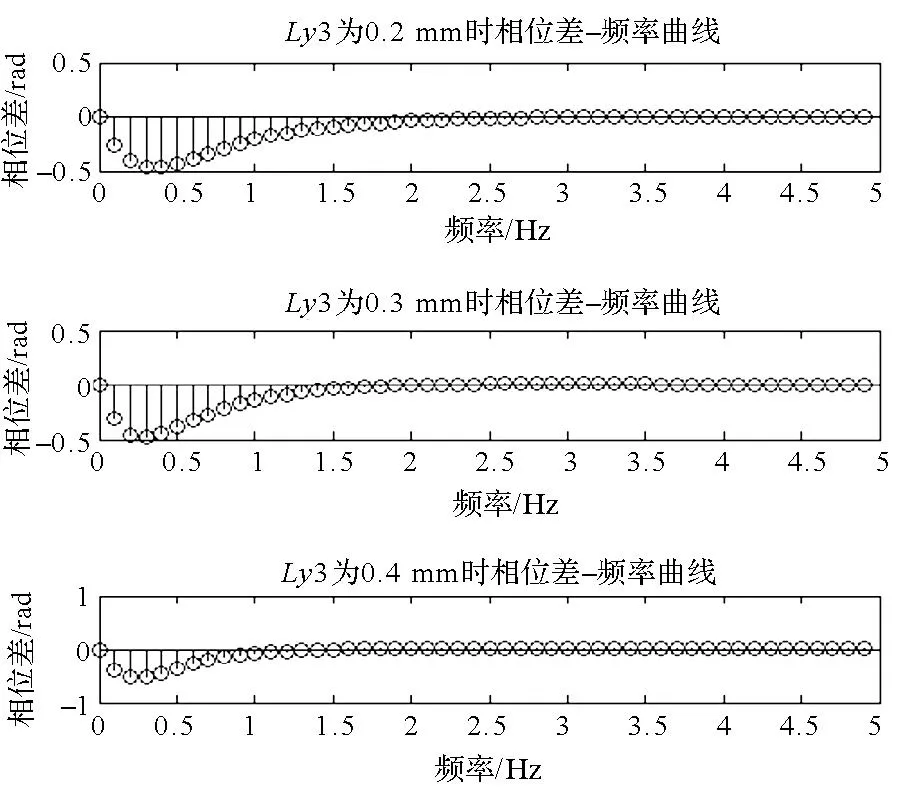
图4　参数Ly3对检测表面相位差的影响Fig.4　Impact of parameter Ly3 on the phase difference

3.4参数Lr1对检测表面相位差的影响

参数Lr1分别取为12.0 mm，12.2 mm，12.4 mm，缺陷(与上一小节相同)对应检测表面与非缺陷(圆柱中心)对应检测表面的相位差分布如图5所示，由图可知，随着参数Lr1值的增大，检测表面的相位差最大值(指绝对值)减小。

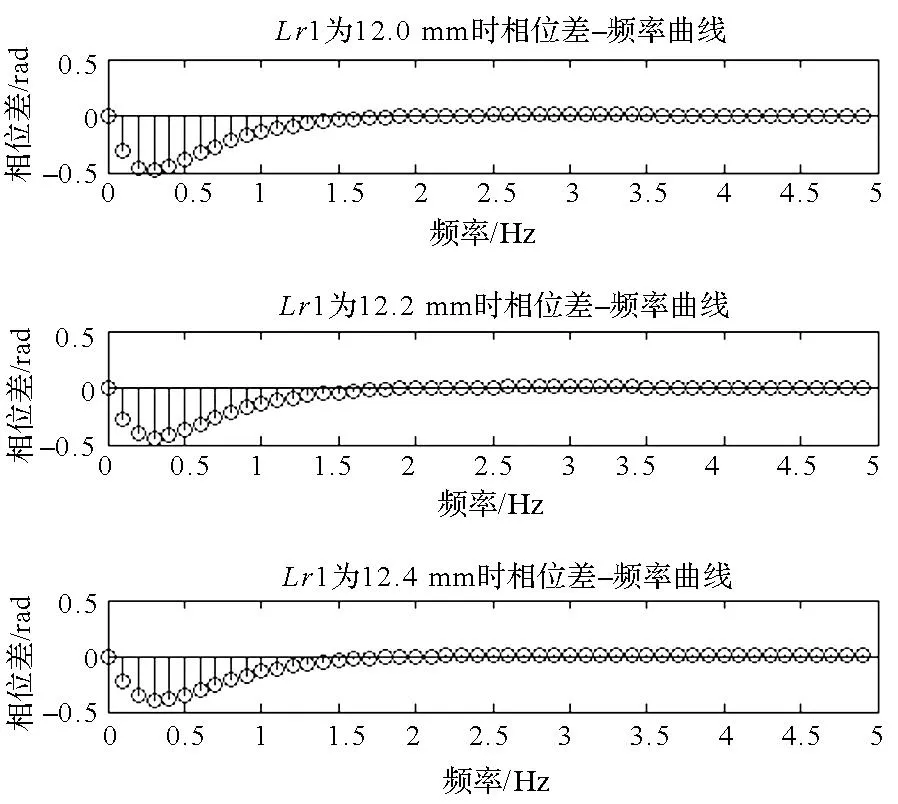
图5　参数Lr1对检测表面相位差的影响Fig.5　Impact of parameter Lr1 on the phase difference

3.5参数Lr2对检测表面相位差的影响

参数Lr2分别取为 6.0 mm，6.2 mm，6.4 mm，缺陷(与上一小节相同)对应检测表面与非缺陷(圆柱中心)对应检测表面的相位差分布如图6所示，由图可知，与参数Lr1相同，检测表面的相位差最大值(指绝对值)随着参数Lr2值的增大而减小。

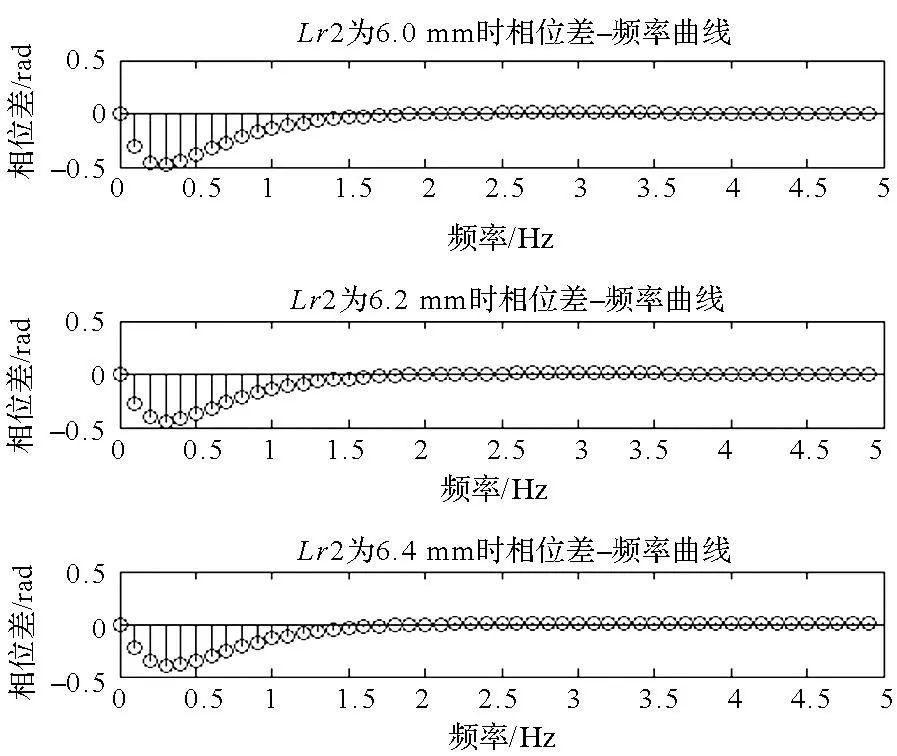
图6　参数Lr2对检测表面相位差的影响Fig.6　Impact of parameter Lr2 on the phase difference

4定量检测算例及分析

在进行热障涂层厚度和材料内部缺陷位置大小的定量识别时，首先假定一组热障涂层厚度和材料内部缺陷位置大小的真实值，由导热方程式(1)～(5)计算出检测表面的真实温度，再如式(10)所示将测温误差添加到真实值上，以此值作为实际测得的温度，对温度进行FFT，得到检测表面的相位(反演识别时的相位值为角度值)，并以此作为定量识别的依据，然后再假设一组热障涂层厚度和材料内部缺陷位置大小的初始值，通过迭代计算得到最终定量检测结果。

Yi=Yi,true+e+ωσ

(10)

式中，Yi为在第i个离散点的测得温度，Yi,true为第i个离散点的真实温度值，e为均匀误差，σ为偏差程度，ω为-1.0到1.0内的随机数。

为了判断识别结果的准确性，定义如式(11)所示的相对误差：

(11)

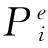
在实际红外无损检测时，检测表面可能存在加热不均，为了研究检测表面加热不均对识别结果的影响，将一个随机偏差添加到加载的热流上，以此来模拟实际红外无损检测时检测表面加载的热流，如式(12)所示。

(12)

当测温不存在误差时，在不同初始假设值下，热障涂层厚度和材料内部缺陷位置大小的识别结果如表2所示(其真实值分别为Lr1=12 mm，Lr2=6 mm，Ly1=1.5 mm，Ly2=0.6 mm，Ly3=0.3 mm)，从表中可以看出，当不存在测温误差时，不同初始假设下都能准确地识别热障涂层厚度和材料内部缺陷位置大小，初始假设对识别结果的影响不大。

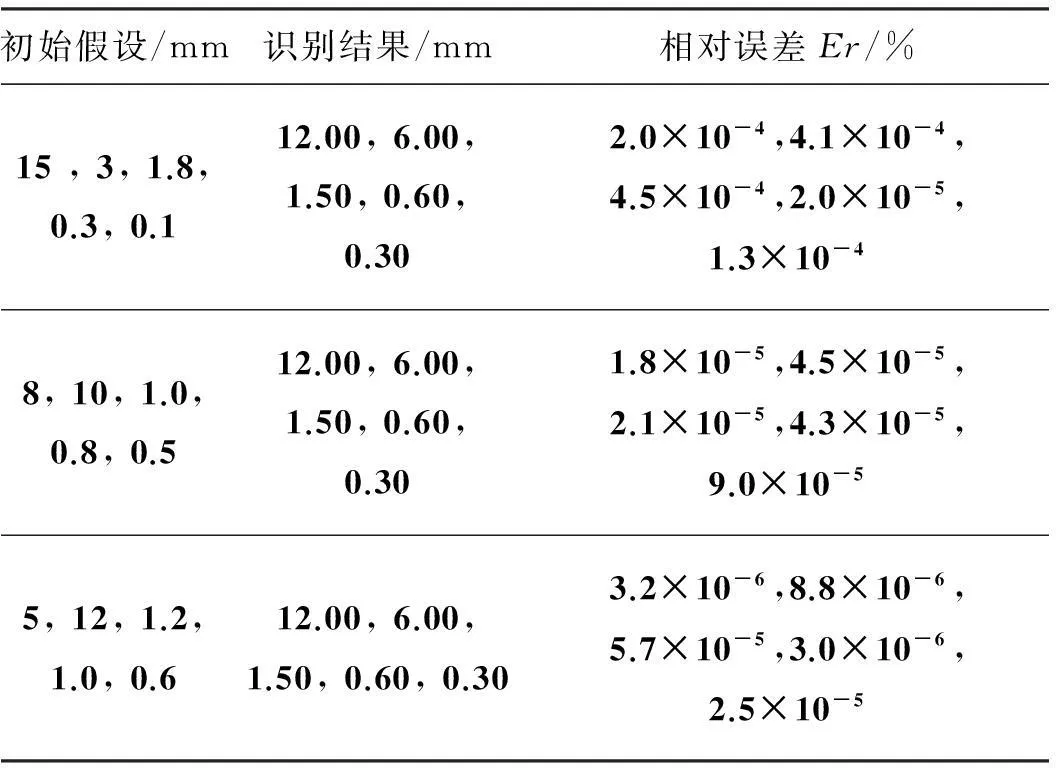
表2　无测温误差时初始假设对识别结果的影响

在实际红外无损检测时，测温会存在测量误差，依据式(10)研究不同形式的测温误差对识别结果精度的影响, 热障涂层厚度和材料内部缺陷位置大小的初始假设分别为Lr1=8 mm，Lr2=10 mm，Ly1=1.0 mm，Ly2=0.8 mm，Ly3=0.5 mm。当只存在均匀误差而无随机误差时，识别结果如表3所示，从表中可以看出，当仅存在均匀误差时，在不同的测温误差下，热障涂层厚度和材料内部缺陷位置大小都能准确识别，均匀误差不改变识别结果，可见均匀误差对识别结果无影响。

当测温存在随机误差而无均匀误差时，热障涂层厚度和材料内部缺陷位置大小的识别结果如表4所示，从表中可以看出，测温误差越小，热障涂层厚度和材料内部缺陷位置大小的识别结果精度越高，随测温误差的增大，识别结果的精度将降低，并且测温误差对不同参数的影响不同，参数Ly1的识别结果受测温误差的影响最大，这种差异性是由于不同参数的扰动对检测表面相位分布的影响程度不同造成的。

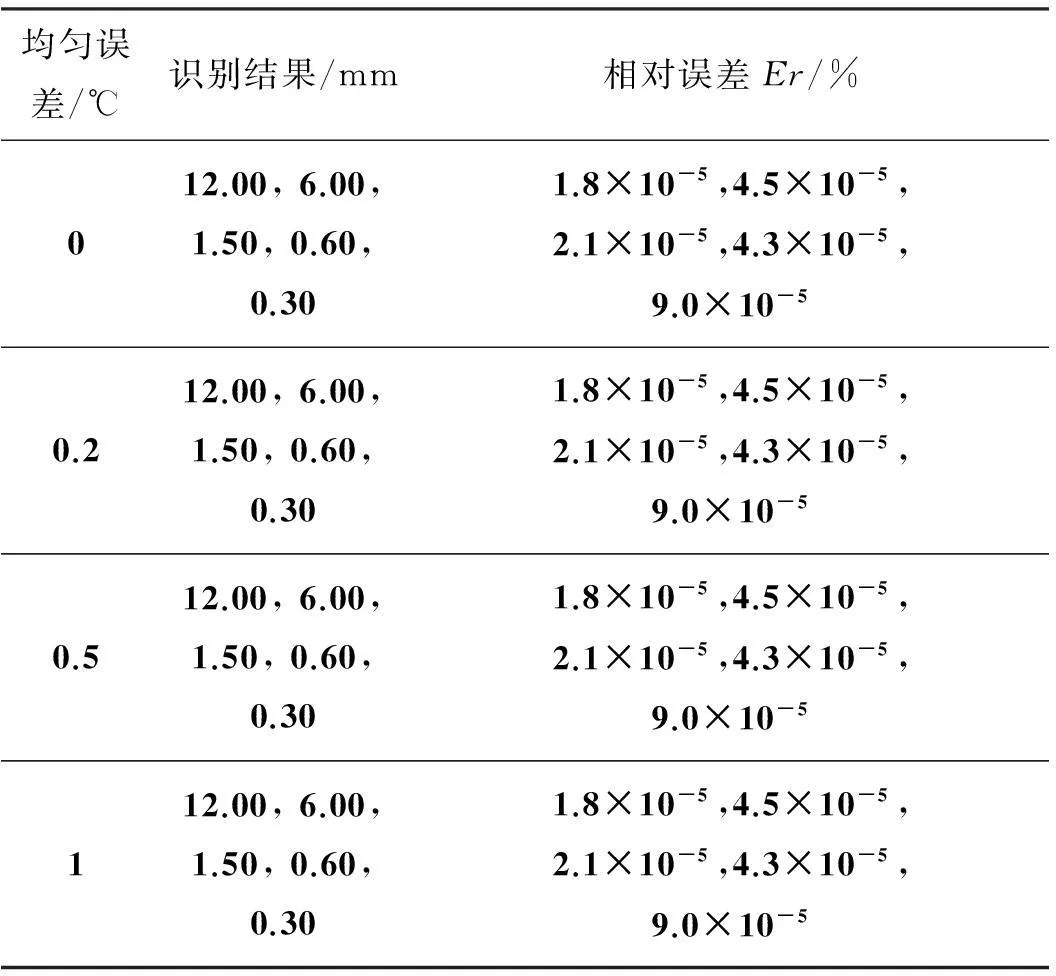
表3　均匀误差对识别结果的影响

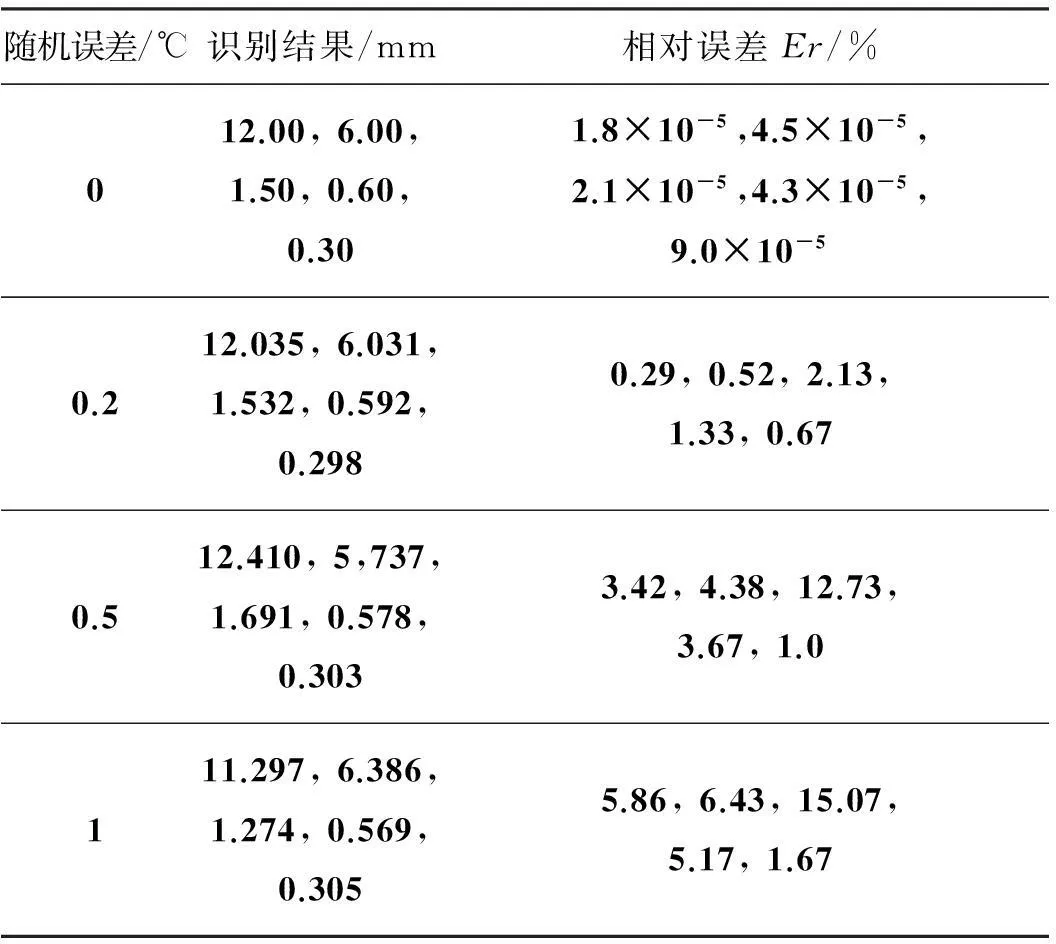
表4　随机误差对识别结果的影响

表5为相同的测温误差(σ=1 ℃)下，不同初始假设对识别结果的影响，从表中可以看出在相同的测温误差下，不同初始假设下的识别结果精度相差不大，可见初始假设对识别结果影响较小。

表5　当存在测温误差时不同初始假设

在实际红外无损检测时，加载的热流可能存在加热不均，依据式(12)的模拟方法研究在相同的测温误差(σ=1 ℃)下不同程度的加热不均对识别结果的影响，识别结果如表6所示。热障涂层厚度和材料内部缺陷位置大小的初始假设分别为Lr1=8 mm，Lr2=10 mm，Ly1=1.0 mm，Ly2=0.8 mm，Ly3=0.5 mm。从表中可以看出，在相同的测温误差下，随表面加热不均的增大，热障涂层厚度和材料内部缺陷位置大小的识别结果精度未出现较明显的降低，可见识别结果精度对加热不均不敏感。

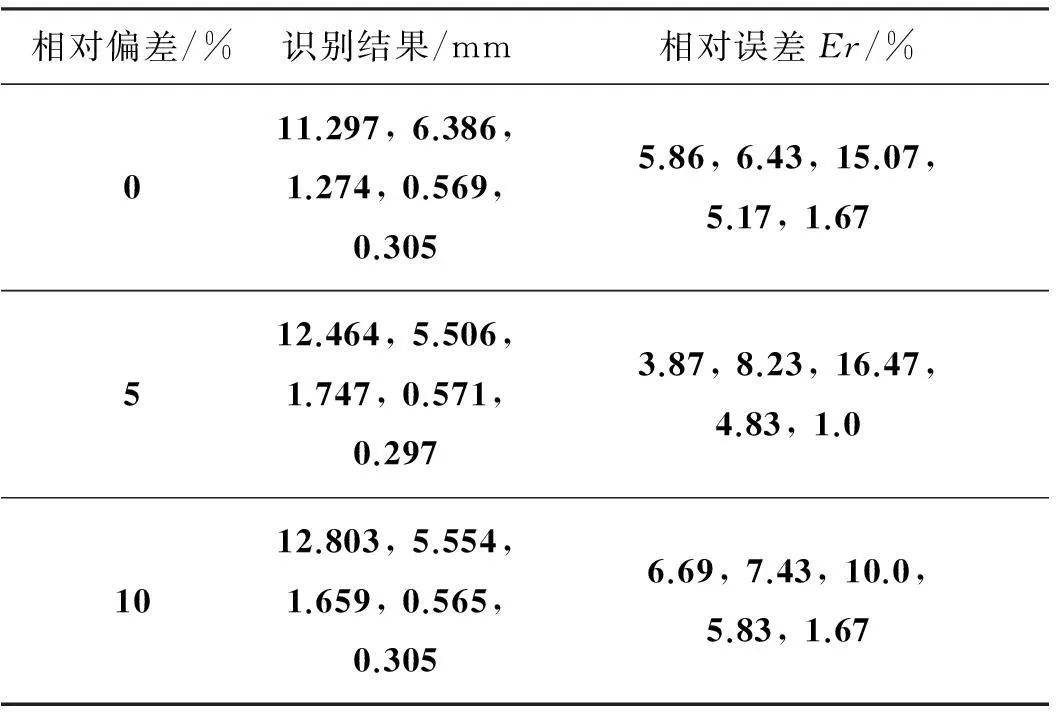
表6　检测表面加热不均对识别结果的影响

5结论

建立了热障涂层厚度及其涂敷下材料内部缺陷的红外检测模型，分析了待检测参数对检测表面相位差的影响，采用LM算法实现了对热障涂层厚度及其涂敷下材料内部缺陷的定量化识别，分析了初始假设、不同测温误差和加热不均对识别结果的影响，得到的结论主要有：

1)检测表面相位差最大值(指绝对值)随材料内部缺陷位置大小参数Lr1，Lr2，Ly1和Ly2的增大而减小，而随着热障涂层厚度参数Ly3的增大而增大，但不同参数的扰动对检测表面相位差分布的影响不同，参数Ly1的扰动对相位差分布的影响最弱。

2)当不存在测温误差时，热障涂层厚度和材料内部缺陷位置大小在不同的初始假设下都有很高的识别精度；当存在测温误差时，在相同的测温误差下，热障涂层厚度和材料内部缺陷位置大小在不同初始假设下的识别结果精度相差不大，可见初始假设对定量识别的影响不大。

3)当测温仅存在均匀误差时，热障涂层厚度和材料内部缺陷位置大小的识别结果精度都很高，识别结果不随测温误差的增大而改变，可见均匀误差对识别结果无影响。

4)当测温仅存在随机误差时，测温误差较小时热障涂层厚度和材料内部缺陷位置大小的识别精度很高，随测温误差的增大，识别结果的精度将降低，但在较大的测温下仍有较高的识别精度，表明了识别方法的有效性；测温误差对不同参数识别精度的影响不同，参数Ly1的识别精度最易受其影响。

5)在相同的测温误差下，随表面加热不均的增大，识别结果的精度未出现较明显的降低，可见识别结果精度对加热不均不敏感。

参考文献(References)

[1]Sayar M, Seo D, Ogawa K. Non-destructive microwave detection of layer thickness in degraded thermal barrier coatings using K-and W-band frequency range[J].NDT&E International, 2009, 42(5): 398-403.

[2]Roge B, Fahr A, Giguere J S R, et al. Nondestructive measurement of porosity in thermal barrier coatings[J].Journal of Thermal Spray Technology, 2003, 12(4): 530-535.

[3]肖劲松, 严天鹏. 风力机叶片的红外热成像无损检测的数值研究[J].北京工业大学学报, 2006, 32(1): 48-52.

XIAO Jingsong, YAN Tianpeng. Numerical analysis of NDT of wind turbine blades using infrared imaging[J]. Journal of Beijing University Technology, 2006, 32(1): 48-52. (in Chinese)

[4]Bai W, Wong B S. Evaluation of defects in composite plate under connective environments using lock-in thermography[J].Measurement Science and Technology, 2001,12(1): 142-150.

[5]马说邯, 马齐爽. 红外脉冲相位复调制细化检测算法[J].红外与激光工程, 2012, 41(8):2223-2225.

MA Shuohan, MA Qishuang. Algorithm of infrared pulse phase thermography multiple modulation zoom spectrum inspection[J]. Infrared and Laser Engineering, 2012, 41(8): 2223-2225. (in Chinese)

[6]Shepard S M, Hou Y L, James R, et al. Thermographic measurement of thermal barrier coating thickness[C]// Proceedings of Thermosense XXVII, SPIE, 2005:407-410.

[7]Franke B, Sohn Y H, Chen X. Monitoring damage evolution in thermal barrier coatings with thermal wave imaging[J]. Surface and Coatings Technology, 2005, 200(5/6):1292-1297.

[8]Tang Q J, Liu J Y, Wang Y, et al. Experimental study of inspection on SiC coated high-temperature alloy plates with defects using pulsed thermographic technique[J]. Infrared Physics & Technology, 2013, 57(3): 21-27.

[9]Tang Q J, Liu J Y, Wang Y, et al. Inspection on SiC coated carbon-carbon composite with subsurface defects using pulsed thermography[J]. Infrared Physics & Technology, 2013,60: 183-189.

[10]Chen W L, Yang Y C. Inverse estimation for unknown fouling-layer profiles with arbitrary geometries on the inner wall of a forced-convection duct[J].International Journal of Thermal Sciences, 2010, 49: 86-98.

[11]Hsieh C K, Su K U. A methodology of predicting cavity geometry based on the scanned surface temperature data-prescribed heat flux at the cavity side[J]. Journal of Heat Transfer, 1981, 103(1): 42-46.

[12]梅林, 吴立德, 王裕文. 一种基于遗传算法的红外无损检测缺陷的新方法[J]. 光学学报, 2002, 22(12): 1452-1456.

MEI Lin, WU Lide, WANG Yuwen. A novel defect evaluation method in infrared nondestructive testing based on genetic algorithm[J]. Acta Optica Sinica, 2002, 22(12): 1452-1456.(in Chinese)

[13]Liu F G. A hybrid method for the inverse heat transfer of estimating fluid thermal conductivity and heat capacity[J].International Journal of Thermal Sciences, 2011, 50(5): 718-724.

[14]Fan C L, Sun F R, Yang Li. A quantitative identification technique for a two-dimensional subsurface defect based on surface temperature measurement[J].Heat Transfer-Asian Research, 2009, 38(4): 223-233.

[15]丁彰雄. 热障涂层的研究动态及应用[J].中国表面工程, 1999(2): 31-37.

DING Zhangxiong. Research status of thermal barrier coatings and application[J].China Surface Engineering , 1999(2): 31-37.(in Chinese)

Infrared quantitative identification for thickness and material inner defects of thermal barrier coating

CHENLin1,2,YANGLi1,FANChunli1,SHIHongchen1,ZHAOXiaolong1

(1. College of Power Engineering, Naval University of Engineering, Wuhan 430033, China;2. Bengbu Naval Petty Officer Academy, Bengbu 233012, China)

Abstract：Aiming at the problems of infrared quantitative detection of thermal barrier coating structures, the LM recognition algorithm based on pulse phase was put forward. The transient thermal model of thermal barrier coating structures was established in an axisymmetric cylindrical coordinate in view of the research problem. The surface temperature field of the research model was calculated by the finite volume method. Then the phase distribution of the inspection surface was obtained through a fast Fourier transform. The impacts of parameters to be detected on the phase difference of the inspection surface were analyzed. Taking the phase as identification condition, the quantitative identification of coating thickness and material inner defects was conducted by using LM inversion algorithm. The effectiveness of LM identification method on the basis of phase detection was evidenced by the numerical experiment results.

Key words：thermal barrier coating; infrared testing; quantitative identification; pulse phase

中图分类号：TK38

文献标志码：A

文章编号：1001-2486(2016)01-107-07

作者简介：陈林(1986—)，男，湖北洪湖人，博士研究生，E-mail：chenlinhonghu@163.com；杨立(通信作者)，男，教授，博士，博士生导师， E-mail：lyang39@hotmail.com

基金项目：国家自然科学基金资助项目(50906099,51479203)

*收稿日期：2015-02-06

doi:10.11887/j.cn.201601018

http://journal.nudt.edu.cn