酸雨环境下砌体结构地震易损性研究①

郑山锁， 程明超， 马德龙， 牛丽华， 郑　捷

(西安建筑科技大学土木工程学院，陕西 西安 710055)



酸雨环境下砌体结构地震易损性研究①

郑山锁， 程明超， 马德龙， 牛丽华， 郑捷

(西安建筑科技大学土木工程学院，陕西 西安 710055)

摘要：对4榀相同特性的砖墙进行不同程度的酸雨腐蚀试验及低周反复荷载试验，得出其在不同腐蚀循环次数下的滞回曲线。基于陆新征-曲哲恢复力模型对砖墙试件进行模拟分析，并与试验结果进行对比，验证得出三弹簧单元模型能够较准确预测砌体构件的滞回性能。利用三弹簧单元模型对不同腐蚀次数下砌体结构进行IDA分析，得出不同腐蚀次数下砌体结构的易损性曲线，通过对“小震”、“中震”、“大震”下结构失效概率的分析得出，酸雨腐蚀能够严重影响结构的力学性能，使得结构的抗震性能显著下降。

关键词：三弹簧单元模型； 酸雨； 砌体结构； IDA； 地震易损性

0引言

砌体结构作为一种各项异性的复合材料，对其进行非线性分析一直面临着复杂性与精确性两大问题。近年来随着计算机水平的发展和数值算法的日益完善，采用不同单元类型(壳单元和实体单元)、不同建模方法(离散元模型和连续介质模型)和不同计算方法(隐式积分法和显式积分法)的有限元数值模拟方法越来越多，其有限元分析发展经历由简单到复杂、由二维到三维分析的过程。王珊等[1]通过自行编制的“砖混结构平面有限元分析软件”对砌体墙片进行演算，并与试验结果进行了对比；王述红等[2]采用东北大学开发的MFPA2D系统，基于弹塑性损伤模型研究了砌体的破坏规律；马宏旺等[3]利用ABAQUS软件对农村砌体结构进行了详尽的地震时程分析；刘振宇等[4]将RVE均质化方法运与ANSYS软件对砌体进行分析，取得了有益的结果。

另一方面，由于近代重工业及汽车工业的迅猛发展，大量的硫化物和氮氧化合物被排放到空气中，经过与空气中水汽的化学反应转变为酸雨。近些年来，全国发生酸雨的范围越来越大，酸雨俨然成为影响砌体结构耐久性的主要原因之一。据历次震害统计资料显示砌体结构所受的破坏比例最大，遭受的损失最为严重[5-6]。因此，进行酸雨环境下砌体结构的地震易损性分析，建立酸雨环境恶劣地区在役砌体结构的抗震性能衰减规律具有重要的实用意义。

为研究酸雨环境下砌体结构的地震易损性，本文基于陆新征-曲哲恢复力模型建立不同腐蚀次数下砖墙的滞回性能，并与试验结果进行对比，以验证模型的准确性；利用三弹簧单元模型对砌体结构进行建模，能够较好地反映结构的基本动力特性。通过对砌体结构进行IDA分析，得出不同腐蚀次数下砌体结构的易损性曲线，通过对该曲线的分析可以得出，酸雨腐蚀能够严重影响结构的力学性能，使得结构的抗震性能显著下降。

1砖墙构件数值模拟

1.1三弹簧单元模型简介

目前针对剪力墙结构体系的非线性分析，常用的有限元模型有等效框架模型、三垂直杆元模型、多垂直杆元模型及等效拉杆模型等。这些模型的主要思路均是采用部分杆件或弹簧来模拟墙体的抗弯与抗剪性能，再通过一些参数的调整来实现杆件或弹簧的刚度和强度与实际情况相符，从而实现三种变形(轴向变形、弯曲变形和剪切变形)间的相互协调。由于大部分砌体墙的高宽比较小，其破坏模式均以剪切变形为主，因此，本文以三弹簧单元模型来模拟砌体抗震墙的实际情况，水平方向采用一根非线性弹簧来表示墙体的抗剪性能。该弹簧采用陆新征-曲哲10参数恢复力模型来模拟墙体的抗震性能；竖直方向采用2根具有足够刚度的线性弹簧提供墙体的轴向支撑(图1)。

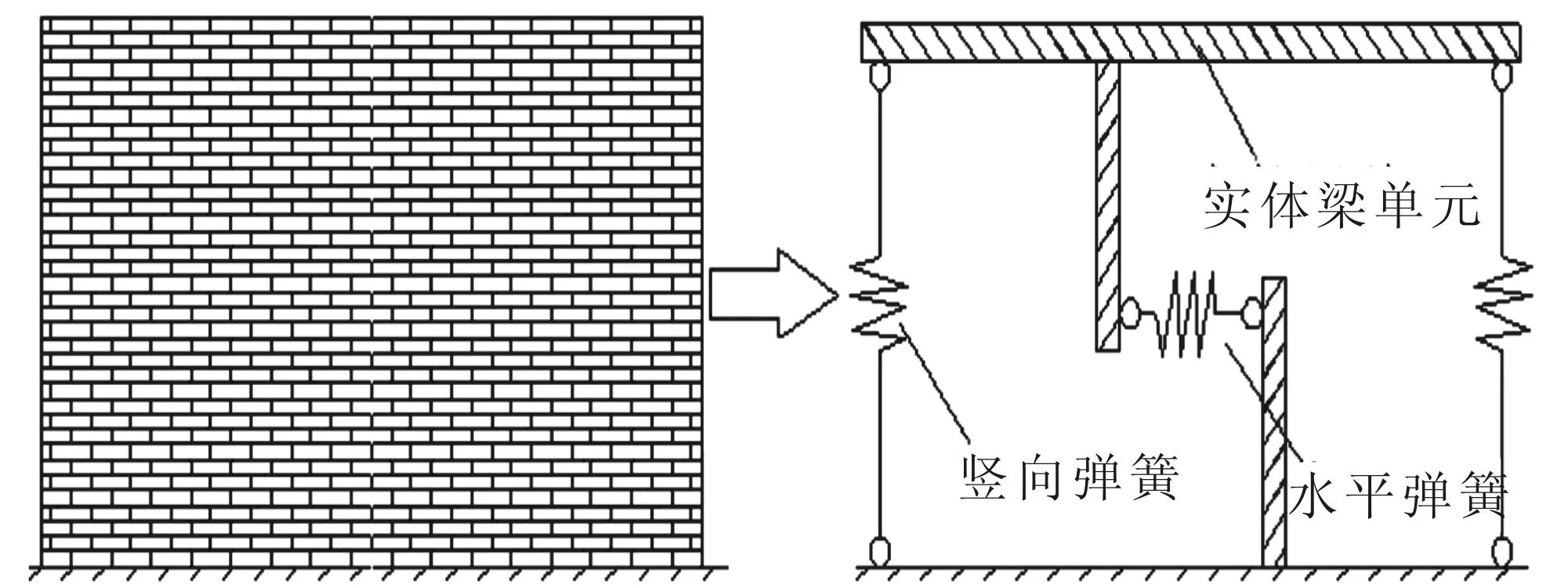
图1　墙体三弹簧模型Fig.1　Three spring model

陆新征-曲哲10参数恢复力模型(图2)最开始应用于混凝土塑性铰的模拟，由于该模型具有丰富的参数变换，因此可作为多个结构形式的恢复力模型进行研究。陆-曲10参数如表1所列。

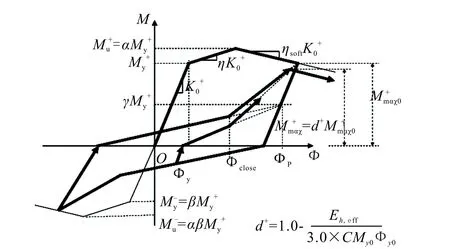
图2　陆-曲恢复力模型Fig.2　Lu-Qu restoring force model

K0初始刚度ηsoft软化系数My正向屈服强度α极限强度与屈服强度的比值η强化模量系数β负向和正向屈服强度的比值C损伤累计耗能系数αk卸载刚度系数γ滑移捏拢系数ω滑移段终点系数

1.2试验概况

试验共设计四榀墙体试件，其设计制作、腐蚀以及加载均在西安建筑科技大学结构抗震实验室进行。试件模型见图3，试验流程见图4所示。

图4　试验流程Fig.4　Test process

其中，酸雨溶液的pH=3.5，主要成分为H2SO4和HNO3，二者的比例为9:1。酸雨腐蚀制度见图5，

图5　酸雨腐蚀制度Fig.5　Corrosion system of acid rain

通过对砖、砂浆和墙体试件进行0次(WR-1)、100次(WR-2)、200次(WR-3)、300次(WR-4)的酸雨循环腐蚀及材性试验和拟静力试验，得到砖和砂浆的力学性能(表2)以及墙体的滞回曲线(图6)。

图6　砖墙的滞回曲线Fig.6　Hysteresis curves of brick walls

循环次数砂浆强度/MPa砖强度/MPa抗剪强度/MPa抗压强度/MPa弹性模量/MPa012.6816.375.9710.668503010013.9215.746.0820.684468520012.7814.525.4240.582409030010.7413.064.2180.4773850

1.3模型验证

采用三弹簧单元模型基于Marc有限元软件进行建模，由于三弹簧没有质量，需要在模型中定义实体单元，采用顶端设置实体梁单元的方法，将墙体的质量换算到梁单元上。通过对竖向弹簧定义刚度来限制其在垂直方向上的运动，水平弹簧通过软件中的用户自定义模式。陆-曲恢复力模型10参数根据文献[7]标定如表3所列。

表 3　数值模拟得出陆-曲模型10参数

将结果文件wall.t16处理得到模拟值与试验值,并进行对比(图7)。

图7　试验值与模拟值的对比Fig.7　The comparison between test value and　　　 simulation value

通过图7可以看出，陆-曲恢复力模型能较好地反映砌体材料本身的特性，在刚度和极限强度等特征点上相当吻合，曲线中的捏缩滑移等特征也具有较强的吻合度，说明所采用的三弹簧单元模型能够准确预测砌体构件的滞回性能。

2结构层次有限元分析

为验证利用三弹簧单元模型进行结构整体建模的合理性，将文献[8]中的教学楼模型与本文三弹簧单元模型(图8)的计算结果进行对比。

图8　实体模型图与三弹簧模型简化图Fig.8　Sketch map of solid model and three spring model

图9　ABAQUS和MARC中结构前三阶振型图Fig.9　The first three vibration modes in ABAQUS and MARC

结构在外部激励下的动力反应和结构本身的动力特性密切相关，因此对结构进行地震响应分析应首先进行结构自身动力特性分析。模态分析是一种研究弹性结构自身动力特性的方法，可以根据结构的固有频率(包括圆频率)、阻尼和模态振型等动力学特性来描述结构的动力响应过程，在线性结构地震分析中已经成为最常用和最有效的手段。对比ABAQUS和MARC中的模态前三阶振型如图9所示。

将结构前十阶的模态振动周期提取出来如表4所列，其十阶模态振动周期对比如图10所示。

文献[9]提供的砌体结构基本周期的经验计算公式为：

(1)

式中:T1为结构第一周期值;H0为结构总高度。

图10　不同振型阶次的自振周期对比Fig.10　Comparison between the natural periods of different　　　　vibration modes

振型阶次12345678910ABAQUS0.1980.1570.1070.090.0810.0750.0750.0710.0650.062MARC0.2010.1710.1190.0880.0770.0650.0540.0520.0490.047

通过式(1)计算出来的基本自振周期为0.204 6 s，与有限元分析软件ABAQUS和MARC的分析结果相差很小，可认为其计算的模态具有可信性。通过表4和图10可以得出：三弹簧单元与实体单元两种模型有较为相似的模态响应，各阶阵型和自振周期吻合较好，并且随着振型阶次的逐渐增大结构的自振周期逐渐减小，且高阶次的自振周期小于三维实体单元模型，这主要是由于三弹簧单元模型无法反映砌体结构的局部振动特性，当振型的阶次较高时，其结构的振动主要是以刚度更大的楼板振动为主。因此认为三弹簧单元能准确地反映砌体结构的基本动力特性，并满足地震作用下非线性动力时程分析的要求。

3砌体结构易损性研究

3.1计算模型的选取

选择一个横墙承重的四层纸材厂更衣室作为算例。其结构的基本信息为：抗震设防烈度 Ⅷ度，设计地震分组为第二组，场地类别为Ⅱ类，结构设计使用年限为50 年，层高均为3.6 m，墙体采用M7.5混合砂浆砌筑，砖强度等级为MU10，内墙厚度为240 mm，外墙厚度为370 mm。更衣室活荷载为2.0 kN/m2，走廊为2.5 kN/m2，不上人时屋面荷载为0.5 kN/m2，楼梯活荷载 2.5 kN/m2。构造柱截面为240 mm×240 mm，圈梁截面尺寸240 mm×300 mm。结构平面布置如图11所示。

图11　结构平面图Fig.11　Structure floor plan

首先将墙片进行分类，根据实体模型图可知墙体主要分为：带构造柱的墙体和不带构造柱墙体以及开洞与不开洞墙体四类。每层抗震墙的抗震特性由上述类型的墙体恢复力模型的叠加组成(图12)。

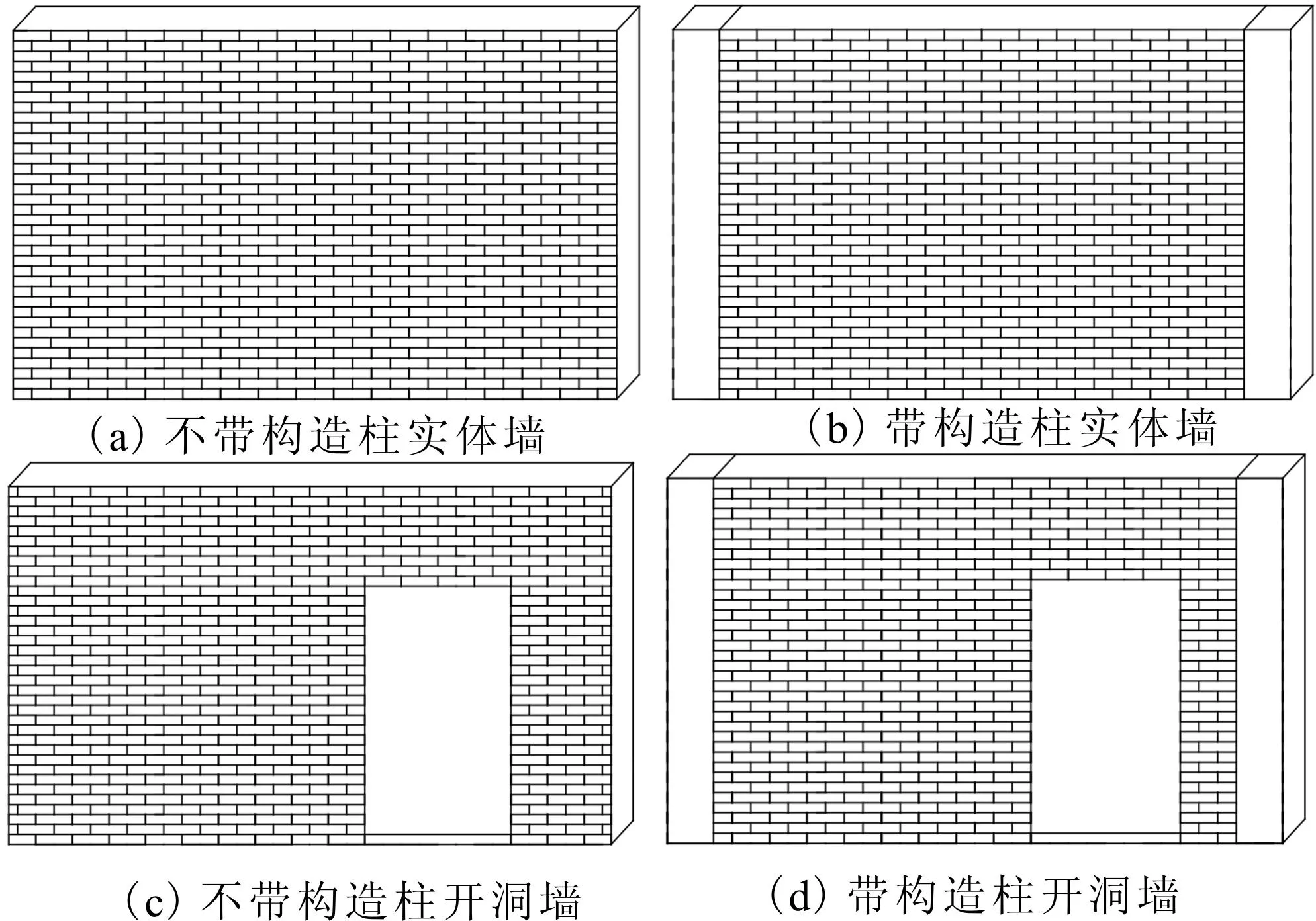
图12　各类墙体示意图Fig.12　Diagram of different kinds of wall

将每一层的各种墙体按照陆-曲模型10参数标定方法标定后，利用三弹簧单元进行建模，其模型能够很好地实现各墙体不同恢复力模型的叠加。为验证模型的可靠性，首先进行模态分析，整个模态的前三阶包括两个方向上的剪切平动振型以及一个三阶扭转振型，表明其结构的刚度与质量布置较为合理；将T1(0.259 s)与文献[9]建议的自振周期公式计算值(0.262 s)进行对比，其相对误差在5%以下，由此可见，结构具备较为准确的动力响应。

3.2地震波的选取

由于地震发生的不确定性，不同强震记录包含不同的频谱、强度以及持时特性，因此单个强震记录的IDA分析并不能全面地分析结构在未来地震中的性能。因此，本文根据ATC-63[10]的选波原则，在美国太平洋地震研究中心网站选取15条地震波对砌体结构进行IDA分析，其地震动记录如表5所列。

表 5　地震动记录

3.3地震损伤指标的确定

对于砌体结构地震反应损伤指标的确定国内外学者做出了大量研究，其主要破坏准则包括：强度指标破坏准则、延性系数指标破坏准则、位移指标破坏准则和变形与能量双重破坏准则。其中位移指标包括位移和层间位移角两种指标。

现阶段国内外许多学者利用层间位移角来考虑砖砌体墙的损伤状态，表6为收集的各试验值以及建议值。

表 6　破坏状态与层间位移角的关系

通过表6可以发现，采用层间位移角作为结构的损伤指标存在较大的离散型，且不同试验研究定义的损伤状态并不统一。因此本文建议将层间位移角进行四个性能水平的划分，其对应结构的状态如表7和图13所示。

图13　砌体结构损伤状态Fig.13　Damage state of masonry structure

本文以朱伯龙试验研究为基础，结合本文试验及砌体结构设计规范的要求，将其层间位移角指标定为表8所列。

3.4概率需求模型的建立

根据文献[17]对结构进行IDA分析，得到最大层间位移角θmax和峰值加速度PGA的拟合式(2)，其需求曲线见图14。

表 7　砌体结构的性能水平

图14　结构需求曲线Fig.14　Demand curves of structure

表 8　层间位移角限值

3.5易损性结果分析

由文献[18]得结构的超越概率由式(3)计算：

(3)

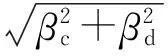
将式(2)代入式(3)，得到不同腐蚀循环次数下结构各破坏状态的超越概率，见式(4)~(7)。

不同腐蚀循环次数下结构的易损性曲线如图15所示。

由图15可以看出，随着腐蚀次数的增加，曲线LS1、LS2、LS3、LS4均向左上方移动，说明结构的抗震能力明显下降。

(4)

(5)

(6)

(7)

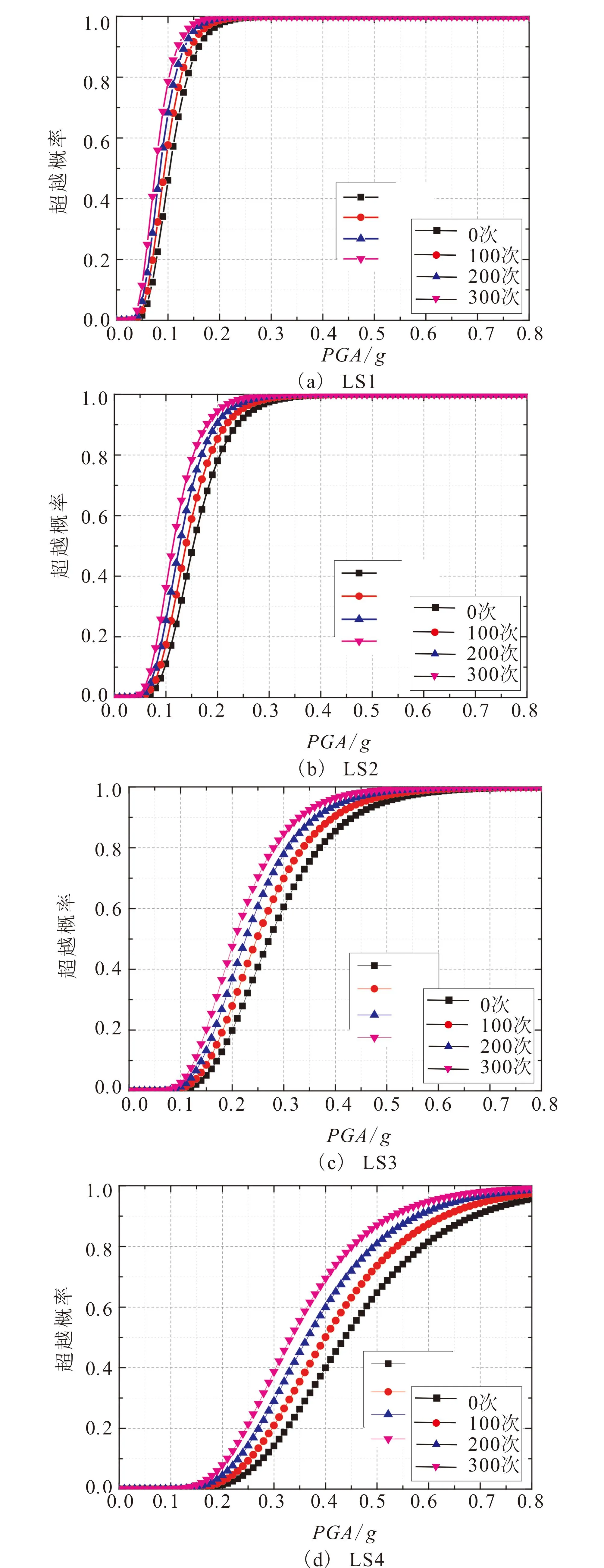
图15　不同腐蚀次数下结构的易损性曲线对比Fig.15　Comparison between structure vulnerability　　　 curves with different corrosions

为了更好地反映随着腐蚀次数的增加结构在各破坏状态下失效概率的变化，本文分别选取Ⅷ度设防下小震(70 cm/s2)、中震(200 cm/s2)、大震(400 cm/s2)三个地震下不同腐蚀次数、不同破坏状态的概率(表9及图16)。

图16　结构各破坏状态的失效概率Fig.16　Failure probability of different damage state

由图16可知：随着循环次数的增加，小震作用下结构基本完好的概率在逐渐降低，而轻微破坏和中等破坏的概率却逐渐增加；中震作用下结构发生严重破坏的概率增加了6.8%、13.84%以及21.01%；大震作用下结构倒塌的概率迅速增加，失效概率分别增大了10%、19%、29.5%，且腐蚀200次、300次结构的倒塌概率已远远大于50%。表明随着龄期的增加，酸雨腐蚀已严重影响结构的抗震性能。

表 9　小震、中震及大震作用下各破坏状态的失效概率

4结论

(1) 采用陆新征-曲哲恢复力模型能较好地反映砌体材料本身的特性，在刚度和极限强度等特征点上相当吻合，曲线中的捏缩滑移等特征也具有较强的吻合度，说明所采用的三弹簧单元模型能够较准确预测砌体构件的滞回性能。

(2) 三弹簧单元与实体单元两种模型有着较为相似的模态响应，可认为三弹簧单元能准确地反映砌体结构的基本动力特性，并能够满足地震作用下的非线性动力时程分析的要求。

(3) 以层间位移角作为砌体结构的破坏指标虽然较为简便，但因不同的砌体结构破坏时较为离散，其指标存在较大的差异。本文总结了国内外的位移指标，并结合试验结果和规范对其进行了重新标定。

(4) 对结构进行IDA分析，得出不同腐蚀次数下砌体结构的易损性曲线，对结构进行小震、中震及大震状态下各状态的破坏概率的对比可得出：结构随着循环次数的增加其结构的对应性能的失效概率逐渐增大，酸雨腐蚀已严重影响结构的整体抗震性能。

参考文献(References)

[1]王珊,武建华.砖砌体的非线性计算[J].重庆建筑大学学报，2001,23(1):10-16.

WANG Shan,WU Jian-hua.Nonlinear Calculation of Brick Masonry[J].Journal of Chongqing Jianzhu University，2011,23(1):10-16.(in Chinese)

[2]王述红,唐春安,吴献.砌体开裂过程数值模型及其数值模拟分析[J].工程力学，2005,22(2):56-61.

WANG Shu-hong,TANG Chun-an,WU Xian.Numerical Model and Simulation of Masonry Fracture Process[J].Engineering Mechanics，2005,22(2):56-61.(in Chinese)

[3]马宏旺,王兰民,陈龙珠，等.农村住宅砌体结构地震破坏数值模拟研究[J].地震工程学报，2013,35(2):232-239.

MA Hong-wang,WANG Lan-min,CHEN Long-zhu,et al.Numerical Simulation of Earthquake Damage in Rural Masonry Buildings[J].China Earthquake Engineering Journal,2013,35(2):232-239.(in Chinese)

[4]刘振宇,叶燎原,潘文，等.效体积单元(RVE)在砌体有限元分析中的应用[J].工程力学,2003,20(2):31-35.

LIU Zhen-yu,YE Liao-yuan,PAN Wen.Application of RVE in the Finite Element Analysis of Masonry[J].Engineering Mechanics,2003,20(2):31-35.(in Chinese)

[5]清华大学、西南交通大学、北京交通大学土木工程结构专家组.汶川地震建筑震害分析[J].建筑结构学报,2008,29(4):1-9.

Civil and Structural Groups of Tsinghua University,Southwest Jiaotong University and Beijing Jiaotong University. Analysis on Seismic Damage of Buildings in the Wenchuan Earthquake[J].Journal of Building Structures,2008,29(4):1-9.(in Chinese)

[6]刘伟，吴志坚，马宏旺，等.汶川大地震甘肃陇南地区建筑震害调查[J].西北地震学报,2010,32(2):179-185.

LIU Wei,WU Zhi-jian,MA Hong-wang,et al.Damage Investigation of Buildings in Southern Gansu Province during the WenchuanMS8.0 Earthquake[J].Northwestern Seismological Journal, 2010,32(2):179-185.(in Chinese)

[7]许浒.大开间多层砖砌体结构抗地震倒塌性能研究[D].成都：西南交通大学,2013.

XU Hu.Analysis on Seismic Collapse Resistant Behavior of the Large-bay Multistory Brick Masonry Structures[D].Chengdu:Southwest Jiaotong University,2013.(in Chinese)

[8]徐振清.圈梁构造柱约束砌体结构的抗震性能分析[D].大连:大连理工大学,2012.

XU Zhen-qing.Seismic Performance Analysis of Confined Masonry[D].Dalian: Dalian University of Technology,2012.(in Chinese)

[9]杨玉成.多层砖房的地震破坏和抗裂抗倒设计[M].北京：地震出版社,1981.

YANG Yu-cheng.Seismic Damage and Crack Resistance Design of Multi-story Brick Masonry[M].Beijing:Seismological Press,1981.(in Chinese)

[10]ATC-63,Quantification of Building Seismic Performance Factors,ATC-63 Project Report (90% Draft)[R].FEMA P695/April 2008.

[11]辛高伟.基于 Pushover 方法的砌体结构中小学建筑抗震性能评估[D].西安：西安建筑科技大学,2009.

XIN Gao-wei. Seismic Evaluation of Masonry Structures Based on Push-over Method for Primary and Middle School Building[D].Xi’an: Xi’an University of Architecture and Technology,2009.(in Chinese)

[12]朱伯龙,吴明舜,余安东.砖石及钢筋混凝土框架房厗的变形状态[J].结构工程师,1987(1):47-51，59.

ZHU Bo-long,WU Ming-shun,YU An-dong. Deformation Form of Brick and Reinforced Concrete Frame Building[J].Structure Engineer,1987(1):47-51，59.(in Chinese)

[13]熊立红.多层混凝土砌块结构形态抗震研究[D].哈尔滨:中国地震局工程力学研究所,2004.

XIONG Li-hong.Study on Seismic Performance of Small Hollow Concrete Block Buildings[D].Haibin:Institute of Engineering Mechanics,China Earthquake Administration,2004.(in Chinese)

[14]Hazus MR4 Technical Manual[M].Washington D C,2003.

[15]Ruiz-Garcia J,Miranda E.Inelastic Displacement Ratios for Evaluation of Existing Structures[J].Earthquake Engineering and Structural Dynamics,2003,32(9):1237-1258.

[16]Zahra Riahi,Kenneth J Elwood,Sergio M Alcocer.Backbone Model for Confined Masonry Walls for Performance-based Seismic Design[J].Journal of Structural Engineering,2009,135(6)：645-654.

[17]王丹.钢框架结构的地震易损性及概率风险分析[D].哈尔滨：哈尔滨工业大学, 2006.

WANG Dan.Seismic Fragility Analysis and Probabilistic Risk Analysis of Steel Frame Structures[D].Harbin: Harbin Institute of Technology，2006.(in Chinese)

[18]薛梅.新旧规范设计的砌体结构地震易损性分析[D].重庆:重庆大学,2013.

XUE Mei.Seismic Vulnerability Analysis of Masonry Structure Designed according to the Current Codes and the Former Generation Codes[D].Chongqing: Chongqing Unviersity,2013.(in Chinese)

[19]刘猛.基于易损性的砌体结构抗震抗倒塌研究[D].长沙：湖南大学,2011.

LIU Meng.Seismic Collapse Study of Masonry Structure Based on Fragility[D].Changsha:Hunan University,2011.(in Chinese)

Seismic Vulnerability of Masonry Structures Subjected to Acid Rain

ZHENG Shan-suo, CHENG Ming-chao, MA De-long, NIU Li-hua, ZHENG Jie

(SchoolofCivilEngineering,Xi’anUniversityofArchitectureandTechnology,Xi’an710055,Shaanxi,China)

Abstract:Because of environmental pollution, the frequency of acid rain is increasing. In rural areas and small towns in China, many ancient buildings are masonry structures that are easily corroded by acid rain. Because of the poor seismic performance of masonry structures subjected to acid rain, research on these structures corroded by acid rain has become increasingly important. In this study, we designed four brick walls with common characteristics and tested them with a series of 0, 100, 200, and 300 corrosion cycles of acid rain. Then, using a low reversed cyclic loading test, we obtained the hysteresis curve of the four brick walls under these corrosion cycles. Based on the three-spring element model combined with the Lu Xinzheng-Qu Zhe restoring force model, we used the finite element software Marc to simulate the response of the brick walls. Our experimental results proved that the three-spring element model can accurately predict the hysteretic properties of masonry structures. To verify the rationality of using the three-spring element model to simulate the whole structure, we used it to construct a finite element model of a teaching building for modal analysis and compared it with the ABAQUS modal analysis results of previous research. Our results show that the three-spring element model can better reflect basic dynamic structural characteristics and satisfy requirements for nonlinear earthquake analysis. We also summarize domestic and overseas drift allowance angles of different damage states combined with our experimental results and China’s national code to demarcate appropriate drift allowance angles. We used 15 seismic waves from the ATC-63 project to perform an incremental dynamic analysis of structures and to obtain seismic vulnerability curves under different corrosion cycles. Based on our analysis of the failure probability for different structural damage states from small, medium, and large earthquakes, acid rain can seriously affect structural mechanical properties and significantly reduce seismic performance.

Key words：three-spring element model; acid rain; masonry structure; incremental dynamic analysis (IDA); seismic vulnerability

DOI:10.3969/j.issn.1000-0844.2016.01.0079

中图分类号:TU362

文献标志码：A

文章编号:1000-0844(2016)01-0079-10

作者简介：郑山锁，男，博士生导师，教授，主要从事工程结构抗震研究。E-mail：zhengshansuo@263.net。

基金项目：国家科技支撑计划(2013BAJ08B03)；教育部高等学校博士学科点专项科研基金(20136120110003)；陕西省科研项目(2012K-03-01，2011KTCQ03-05，2013JC16)

收稿日期：①2015-06-03