台站地震资料的时频域自适应极化分析和滤波①

马见青， 李庆春， 王卫东， 王美丁， 李春兰

(1.长安大学 地质工程与测绘学院, 陕西 西安 710054; 2.西北有色地质勘查局 物化探总队，陕西 西安 710068)



台站地震资料的时频域自适应极化分析和滤波①

马见青1， 李庆春1， 王卫东1， 王美丁2， 李春兰2

(1.长安大学 地质工程与测绘学院, 陕西 西安 710054; 2.西北有色地质勘查局 物化探总队，陕西 西安 710068)

摘要：提出一种自适应协方差的时频域极化滤波方法。该方法在广义S变换时频方法的基础上，构造时频域自适应协方差矩阵，通过特征分析计算时频域瞬时极化参数，设计极化滤波器，实现多分量地震极化分析和滤波。其优势在于协方差矩阵的分析时窗的长度由多分量地震数据的瞬时频率确定，可以自适应于有效信号的周期，在每个时频点计算极化参数不需要进行插值处理；结合时间频率信息，解决在时间域或频率域波形或频率重叠的信号具有明显的直观性。模型数据及实际三分量台站地震数据处理结果表明，该极化滤波方法在台站地震资料分析和处理方面具有很好的直观性和较高的分辨率。

关键词：极化滤波； 时频分析； 广义S变换； 自适应协方差矩阵； 多分量地震

0引言

不同类型地震波的极化特性不同，地震波场实质上是不同极化特性的振动相互干涉和叠加的结果。极化滤波是在波的极化特性基础上的一种信号处理方法。目前极化分析方法在地球物理领域已经得到了广泛应用。Benhama[1]、李英康等[2]利用空间方向滤波方法来压制面波及分离纵横波；李锦飞等[3-4]利用小波包变换,在时频域通过极化滤波方法对信号进行处理, 以达到从实际运动波场中分离出有用波, 消除干扰波和无用波的目的。张建军等[5]用极化分析法提取有效瑞利波信号。葛勇等[6]、Schimmel等[7]利用极化滤波技术提取线性极化波、椭圆极化波及去噪。陈赟等[8]、刘春园等[9]、马见青等[10]利用自适应偏振滤波器剔除三分量地震资料中的随机与非随机噪声。高原等[11]利用极化分析方法进行面波压制及非平面波消除。严又生等[12]、崔汝国等[13]利用极化分析方法对VSP资料进行波场分离和合成。Meissner等[14]、Helbig等[15]利用极化分析方法进行横波分裂分析和各向异性研究。唐晓燕等[16]通过极化分析，找出所期望的波的空间投影方向，使其具有最大的信噪比，从而能够较容易地分辨快、慢横波，提取有效信息。与走时、振幅和波形相比，偏振与发震时刻、震源的辐射图样、地震波的衰减无关，所以偏振层析成像是研究速度结构的一个较为理想的方法，可以通过三分量地震资料的偏振资料(P波、面波偏振)，独立地或与其他资料联合层析、反演地下岩石构造的速度结构。这对深化地球本体或地下介质的认识具有重要的理论意义和实际应用价值[17-20]。Bai等[21-22]、Reading等[23]提出了利用极化分析法进行多波震相自动识别和地震波到时的检测，该方法是根据P波和S波不同的极化特征来识别和确定初动时间的。马见青等[24]对目前发展起来的各种类型的极化分析方法进行分析总结，包括其方法原理、各自的优缺点、应用范围、以及发展前景。

对于基于多分量记录的协方差矩阵或奇异值分解的主分量分析的这些极化分析方法，需要在分析时选择一个时窗[25]。时窗的选择是进行极化分析的关键性步骤。对于含有频散特性的面波的多分量数据以及在时间上有重叠的地震波来说，时窗长度的选择变得更加复杂。因此对于每一段需要分析的地震波来说，时窗长度应该适当选择，以匹配有效信号的优势周期。Diallo等[26]提出了一种在时间域的极化分析法，通过使用自适应时窗，对分析时窗的约束已经放宽了。但在波形初至很接近时，再利用这种单一的时间域方法来刻画不同波型的极化分布就变得比较困难了。

时频分析方法特别适合解决在时间上重叠但有不同频谱的地震信号分离以及瞬时信号分析问题。它可以描述一个信号的频率成分随时间的变化。基于时频分析方法的优点，可以将其应用于极化分析中。姚家骏等[27]利用短时傅里叶变换、S变换、CWD分布及ZAM分布四种时频分析方法对实际台站地震信号进行时频域分析，总结了这四种时频分析方法在分辨地震波中的应用效果及优缺点。许康生等[28]通过小波变换分析近地震波相对能量特征，很好地揭示近地震能量分布在频率域的特征。

本文通过使用广义S变换[29-31]，将Diallo等[26]提出的时间域自适应极化滤波方法引入到时频域，在时频域中计算多分量地震记录中质点振动的极化分布，以取得有明确频率意义的极化分布。该方法建立在协方差矩阵的基础上，用一个近似方程来计算时窗内的协方差矩阵，这个时窗是由多分量记录的瞬时频率确定的，其长度自适应于每个时频点处的地震波的优势周期，然后在每个时频点估计极化特征参数。最后，在时频域中设计合适的滤波器，进行地震信号的分析和处理。

1时频域自适应协方差极化分析方法

对三分量地震信号ui(t)(i=x,y,z)分别做GST，得到各自的时频谱GSTi(t,f)。定义Ωi(t,f)为i分量的瞬时频率函数[32]。

(1)

利用三分量数据的GSTi(t,f)，可以构造时频域中的交叉能量矩阵MS：

(3)

这里均值μkm(t,f)定义为：

(4)

时窗长度Tkm(t,f)由下式确定：

其中：R(·)表示复数的实部；sinc(x)表示辛格函数；N为一正整数，在刻画椭圆极化属性时，选取N=1或2就足够了，当需要刻画三维空间里的结构更为复杂的极化属性时可以选取较大的N值。

矩阵MS(t,f)是在时频域中每个时频点上定义的，对它进行特征值分析，得到特征值λi(t,f)(i=1,2,3)，且λ1≥λ2≥λ3，Vi(t,f)(i=1,2,3)为λi(t,f)对应的特征向量，通过特征值和特征向量计算时频域中的瞬时极化参数。主要的极化参数如下：

瞬时极化轴(瞬时极化主轴、瞬时极化中间轴、瞬时极化次轴)

2滤波算法

随着自适应协方差法推广到时频域，我们可以构造基于瞬时极化分布的极化滤波算法来分离不同类型的地震波。例如可以通过椭圆率ρ(t,f)和仰角θ(t,f)=π/2-δ(t,f)的约束组合构建一个分离体波和面波的滤波算法[32]，该算法表达式如下：

式中：Fe是时频域的滤波因子，作用在原始信号的每个分量上；Pρ和Pθ分别用来限定ρ和θ的变化范围，通过选择Pρ和Pθ的值来得到期望得到的地震波。

在表1中总结了可用于检测具有特定极化特征的信号的滤波器。

3模型数据处理

现对人工合成的一个三分量记录(图1)进行极化分析，进一步解释时频域的自适应协方差极化分析方法。该模型由5个波段构成：A段表示平稳椭圆，B段表示旋转椭圆，C段表示线性极化的情况，D段表示三维空间的平稳椭圆，E段对应于旋转椭球的情况。前三段只在X-Y平面内分布，而后两段则在整个三维空间均存在。

表 1　各类波对应的极化滤波器

图2为用标准协方差方法和自适应协方差方法得到的瞬时极化轴。可以看到，标准协方差方法与自适应协方差方法相比，精度很低，这主要是由于其时窗长度很难准确地选择，也就是说，时窗长度的选取对于标准协方差极化分析法的精度有很大的影响。图3是时频域自适应协方差极化方法得到的极化参数。通过比较可以看到，时间域和时频域方法得到的极化参数具有很好的对应关系，但时间域极化参数不含频率信息，而时频域极化参数由于采用时间-频率的联合表示，具有很好的直观性、较高的分辨率和较强的实用性。

图1　三分量人工合成记录[26]Fig.1　Three-component synthetic record[26]

图2　时间域瞬时极化参数——极化轴Fig.2　Instantaneous polarization attributes in time domain——polarization axis

图3　时频域极化参数——瞬时极化轴Fig.3　Polarization attributes in time-frequency domain——instantaneous polarization axis

4实际三分量台站资料处理

图4是陕西省地震台网2002年记录的三分量实际地震数据，该台站位于34.25° N，108.95° E，高程600 m。图5为各分量相应的广义S变换时频谱，从原始记录和时频谱中可以清楚看到各分量都分布有面波。图6为三个椭圆率的时频谱。

图7为利用极化椭圆率来压制该地震记录的面波。由于地震面波的极化椭圆率比体波大，综合分析三分量地震信号和极化椭圆率的时频谱，选ρs(t,f)>0.18，并将该区域充为零，再与各分量的时频谱相乘，并作广义S反变换，得到图7(c)所示的滤波结果。从图中可以看到瑞利面波得到了有效压制。如果极化椭圆率选择的过大，虽然可以保证线性极化的体波全部保留，但同时会保留部分椭圆极化的面波；反之，如果极化椭圆率选择的过小，虽然可以保证椭圆极化的面波全部压制，但同时会损失部分线性极化的有效体波。因此在实际应用中需要根据地震信号的时频谱，确定地震面波的有效频率范围，结合极化椭圆率的时频谱选取大小合适的极化椭圆率参数值。

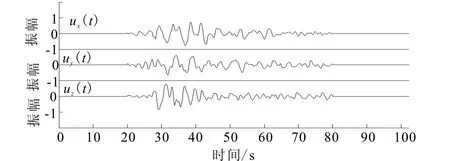
图4　陕西地震台网记录的三分量地震数据Fig.4　The three-component seismogram recorded by　　　 Shaanxi seismic net

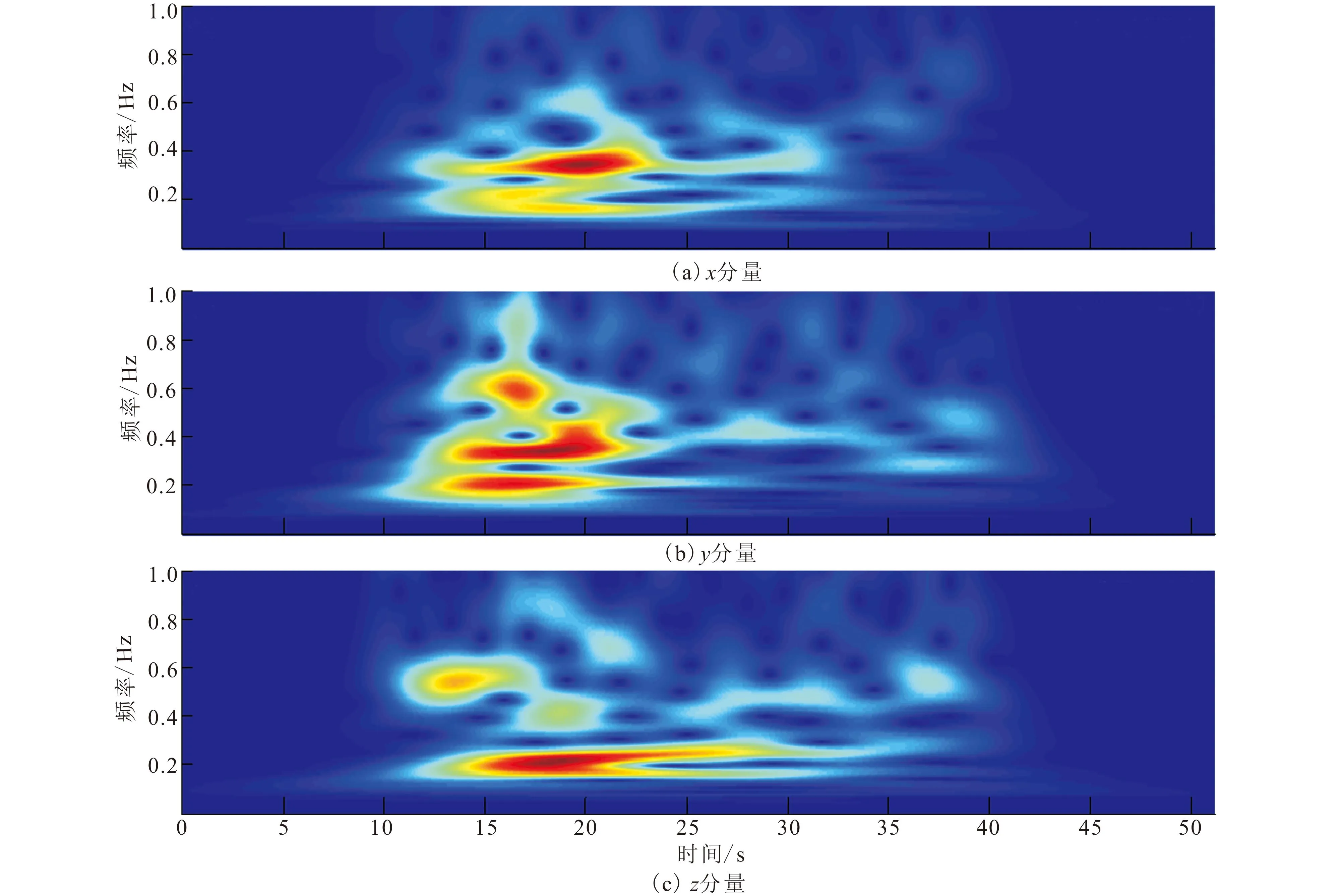
图5　三分量实际数据的时频谱Fig.5　Time-frequency spectrum of the three-component seismogram

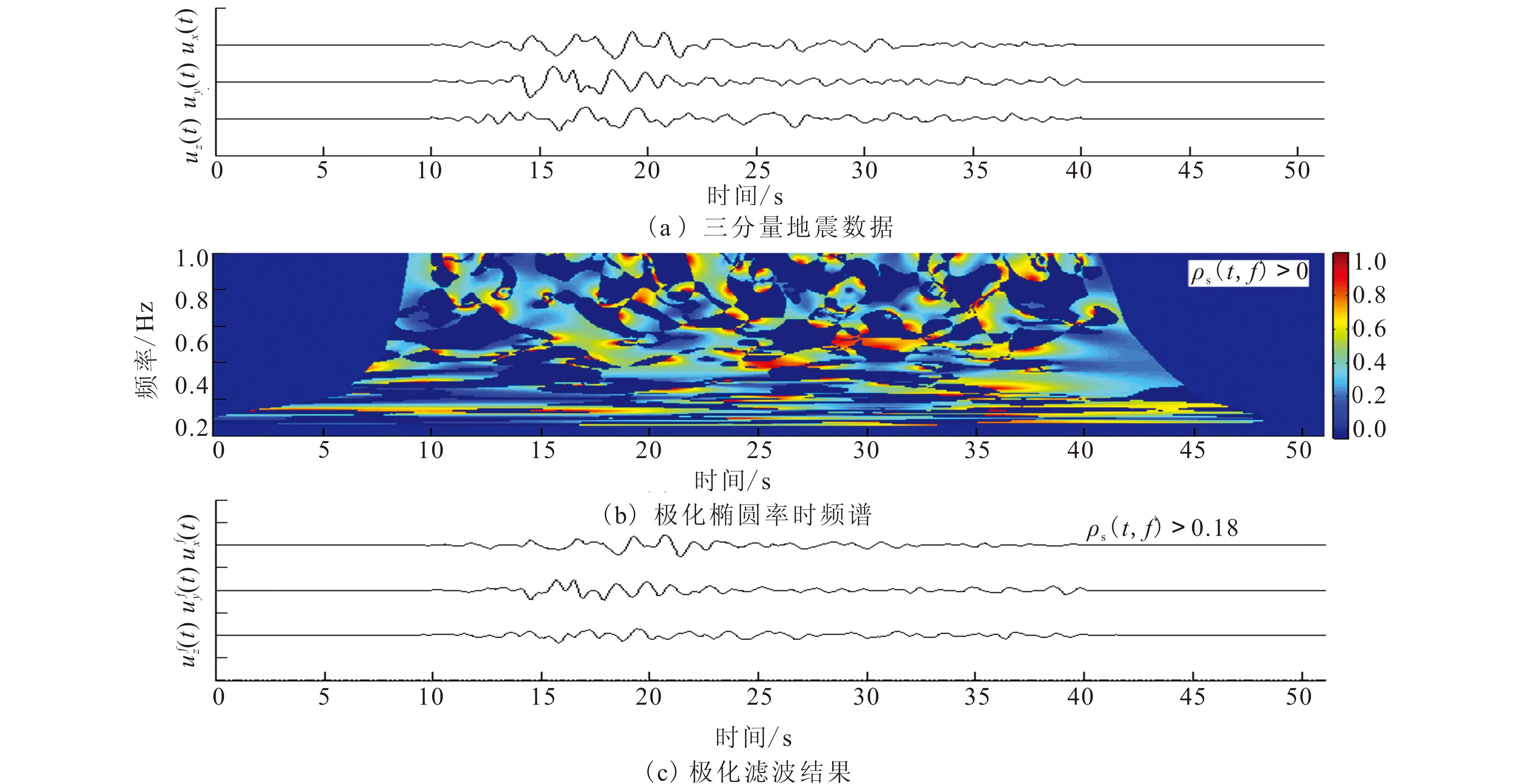
图7　基于极化椭圆率的极化滤波Fig.7　Polarization filtering based on the polarization ellipticity

图8为通过极化倾角进行滤波。垂直极化地震波的极化倾角比水平极化地震波要大，为了压制垂直极化地震波，只需将高极化倾角的区域充为零。图中将极化倾角设置为β(t,f)∈[65°，90°]，保留了与水平极化有关的倾角值，来压制垂直极化的地震波。图8(c)是滤波结果，滤波之后的水平分量的极化波得到了增强，而垂向分量的地震波则几乎完全被压制掉了。如果极化椭圆倾角选择的过大，虽然可以保证水平极化波全部保留，但同时会保留部分垂直极化波；反之，如果极化椭圆倾角选择的过小，虽然可以保证垂直极化波全部压制，但同时会损失部分水平极化的有效波。因此在实际应用中需要结合地震信号和极化倾角的时频谱，综合选取大小合适的极化倾角参数值来压制特定极化方向的地震波。

5结语

本文实现了基于自适应协方差的广义S变换域时频极化分析方法，通过构造滤波器进行波场分离，并讨论了该方法在多分量台站地震资料分析和处理中的应用。

图8　基于倾角的极化滤波Fig.8　Polarization filtering based on the dip angle

该极化分析方法和其他极化分析技术(Rene et al.1986; Morozov&Smithson 1996)是一致的。在理论上，当瞬时频率对于所有分量都一样时，本文方法和用Morozov & Smithson(1996)方法提取的极化参数的结果是一样的。但是，本文提出的方法在范围上更具普遍性，因为它可以描述任意数目分量的极化分布。新颖之处在于把时频分析方法和自适应协方差矩阵方法结合起来。

(1) 该方法建立在协方差矩阵的基础上，用一个近似方程来计算时窗内的协方差矩阵，这个时窗是由多分量记录的瞬时频率确定的，其长度自适应于每个时频点处的波的优势周期。然后在每个时频点估计特征参数，不需要进行插值。

(2) 该方法在每个时频点上计算协方差矩阵元素，因此没必要为了在各点上获得特征参数而处理边界效应。

(3) 实例的处理结果表明，该方法可以在时频域中准确提取各个采样点的所有极化属性，这在实际应用中非常有用。

(4) 明确将极化分布和时频分析方法联系起来，通过在时频域设计中使用滤波器，在整个时频域内进行波场识别和分离，这对于分离体波和面波是非常重要的。而且其他的一些极化属性如方位角、倾角和正负椭圆率等也可以用于改进极化滤波算法。

参考文献(References)

[1]Benhama A, Cliet C, Dubesset M.Study and Applications of Spatial Directional Filtering in Three-component Recordings[J].Geophys,1988,36:591-613.

[2]李英康, 崔作舟.分离纵波和横波的偏振旋转法[J].地球物理学报,1994,37(增刊Ⅱ):372-382.

LI Ying-kang, CUI Zuo-zhou.P and S-waves Separated by Polarization Revolving Method[J].Chinese J Geophys,1994,37(Supp.2):372-382.(in Chinese)

[3]李锦飞, 李人厚, 刘贵忠, 等.基于小波多分辨分析的极化分析和滤波方法[J].信号处理, 1999, 15(1):88-92,97.

LI Jin-fei,LI Ren-hou,LIU Gui-zhong,et al.A Technique on Polarization Analysis and Filtering Based on Wavelet Multiresolution Analtsis[J].Signal Processing,1999,15(1):88-92,97.(in Chinese)

[4]李锦飞, 李人厚.小波包变换空间滤波法分离信号研究[J].煤田地质与勘探,1998,26(4):56-60.

LI Jin-fei,LI Ren-hou.Study on the Signal Separation Using Space Filtering Method Based on Wavelet Package Transform[J].Coal Geology & Exploration,1998,26(4):56-60.(in Chinese)

[5]张建军,李占强.用极化分析法提取有效瑞雷波信号[J].矿业科学技术, 1999(3-4):8-13.

ZHANG Jian-jun,LI Zhan-qiang.Extract Effective Rayleigh Wave Signal Using Polarization Analysis Method[J].Mining Science and Technology,1999(3-4):8-13.(in Chinese)

[6]葛勇,韩立国,韩文明,等.极化分析研究及其在波场分离中的应用[J].长春地质学院学报,1996,26(1):83-88.

GE Yong,HAN Li-guo,HAN Wen-ming,et al.Study and Application of Polarization Analysis in Wave Field separation[J].Journal of Changchun University of Earth Sciences, 1996,26(1):83-88. (in Chinese)

[7]Schimmel M,Gallart J.The Use of Instantaneous Polarization Attributes for Seismic Signal Detection and Image Enhancement[J].Geophysical Journal International,2003,155:653-668.

[8]陈赟,张中杰,田小波.基于加窗Hilbert变换的复偏振分析方法及其应用[J].地球物理学报,2005,48(4):889-895.

CHEN Yun,ZHANG Zhong-jie,TIAN Xiao-bo.Complex Polarization Analysis Based on Windowed Hilbert Transform and Its Application[J].Chinese J Geophys,2005,48(4):889-895.(in Chinese)

[9]刘春园,徐胜峰.极化滤波在三分量噪声衰减中的应用研究[J].地球物理学进展,2009,24(5):1814-1823.

LIU Chun-yuan,XU Sheng-feng.Research on the Three-component Noise Attenuation through Polarization Filtering[J].Progress in Geophysics,2009,24(5):1814-1823.(in Chinese)

[10]马见青，李庆春.提高台站地震资料信噪比的自适应极化滤波[J].地震工程学报,2014,36(2):398-404.

MA Jian-qing,LI Qing-chun.Adaptive Polarization Filtering for Improving the S/N of Station Seismic Data[J].China Earthquake Engineering Journal, 2014,36(2): 398-404.(in Chinese)

[11]高原,蔡燕.极化分析及其在地震勘探中的应用初探[J].江汉石油科技,1997,7(4):11-15,55.

GAO Yuan,CHAI Yan.Polarization Analysis and Preliminary Application in Seismic Exploration[J].Jianghan Petroleum Science and Technology,1997,7(4):11-15,55.(in Chinese)

[12]严又生,宜明理,魏新,等.三维三分量VSP数据处理方法及效果[J].石油地球物理勘探,2005,4(1):18-24.

YAN You-sheng,YI Ming-li,WEI Xin,et al.3D 3C VSP Data Processing Methods and Effects[J].Oil Geophysical Prospecting,2005,4(1):18-24.(in Chinese)

[13]崔汝国,牟风明,宋维琪,等.VSP浮动坐标系偏振滤波[J].石油地球物理勘探,2010,45(1):10-14.

CUI Ru-guo,MOU Feng-ming,SONG Wei-qi,et al.Polarization Filtering in VSP Floating Coordinate System[J].Oil Geophysical Prospecting,2010,45(1):10-14.(in Chinese)

[14]Meissner R,Hegazy M A.The Ratio of the PP-to the SS-reflection Coefficients:A Possible Future Method to Estimate oil and Gas Reservoirs[J].Geophys Prosp,1981,29:533-540.

[15]Helbig K,Mesdag C S.The Potential of Shear Wave Observations[J].Geophys Prosp,1982,30:413-431.

[16]唐晓雪,唐建侯.地震波的偏振分析与应用[J].石油地球物理勘探, 1996,31(增刊2):67-73.

TANG Xiao-xue,TANG Jian-hou.The Polarization Analysis and Application of Seismic Wave[J].Oil Geophysical Prospecting,1996,31(Supp.2):67-73.(in Chinese)

[17]黄忠贤,陈虹,王贵华,等.面波偏振与中国大陆岩石层横向不均匀性[J].地球物理学报,1994,37(4):456-468.

HUANG Zhong-xian,CHEN hong,WANG Gui-hua,et al.Surface Wave Polarization and Lateral Heterogeneities of the Lithosphere in China[J].Chinese J Geophys, 1994, 37(4): 456-468.(in Chinese)

[18]陈虹,黄忠贤.利用时频偏振分析技术研究面波传播的复杂性[J].地震学报,1998,20(2):144-149.

CHEN hong,HUANG Zhong-xian.Study the Complexity of Surface Wave Propagation Using the Time-frequency Polarization Analysis Technique[J].Acta Seismologica Sinica,1998,20(2):144-149.(in Chinese)

[19]王怀军,刘福田,陈晓非.P波偏振层析成像[J].地球物理学进展,2000,15(3):7-13.

WANG Huai-jun,LIU Fu-tian,CHEN Xiao-fei.P-wave Polarization Tomography[J].Progress in Geophysics,2000,15(3):7-13.(in Chinese)

[20]刘福田,胡戈,王怀军,等.由单台远震P波偏振资料反演北京台站邻域的速度结构[J].中国科学：D辑,2000,30(6):642-649.

LIU Fu-tian,HU ge,WANG Huai-jun,et al.Inversion Velocity Structure of Beijing Station Neighborhood from a Single Teleseismic P-wave Polarization Data[J].Scientia in China：Series D,2000,30(6):642-649.(in Chinese)

[21]BAI Chao-ying,Kennett B L N.Automatic Phase-detection and Identification by Full Use of a Single Three-component Broadband Seismogram[J].Bull Seism Soc Am,2000,90:187-198.

[22]BAI Chao-ying,Kennett B L N.Phase Identification and Attribute Analysis of Broadband Seismogram at Far-regional Distances[J].Journal of Seismology,2001,5:217-231.

[23]Reading A M.Polarization Filtering for Automatic Picking of Seismic Data and Improved Converted Phase Detection[J].Geophysical Journal International,2001,147:227-234.

[24]马见青,李庆春,王美丁.多分量地震极化分析评述[J].地球物理学进展,2011,26(3):992-1003.

MA Jian-qing,LI Qing-chun,WANG Mei-ding.Review of Multi-component Seismic Polarization Analysis[J].Progress in Geophysics,2011,26(3):992-1003.(in Chinese)

[25]Morozov I B,Smithson S B.Instantaneous Polarization Attributes and Direction Filtering[J].Geophysics,1996,15:872-881.

[26]Diallo M S,Kulesh M,Holschneider M,et al.Instantaneous Polarization Attributes Based on Adaptive Covariance Method[J].Geophysics,2006,71(5):99-109.

[27]姚家骏,杨立明,冯建刚.常用时频分析方法在数字地震波特征量分析中的应用[J].西北地震学报,2011,33(2):105-110.

YAO Jia-jun,YANG Li-ming,FENG Jian-gang.Application of Common Time-frequency Analysis Methods in Analyzing Characteristic Quantity of Digital Seismic Wave[J].NorthWestern Seismological Journal,2011,33(2): 105-110.(in Chinese)

[28]许康生,李英,李秋红.近地震波的小波相对能量分布特征分析[J].地震工程学报,2013,35(1):166-170.

XU Kang-sheng,LI Ying,LI Qiu-hong.Distribution Characteristics of Wavelet Relative Energy on Near-earthquake Wave[J].China Earthquake Engineering Journal,2013,35(1): 166-170.

[29]Stockwell R G,Mansinha L,Lowe R P.Localization of the Complex Spectrum: the S transform[J].IEEE Transactions on Signal Processing,1996,44(4):998-1001.

[30]Pinnegar C R,Mansinha L.The S-transform with Windows of Arbitrary and Varying Shape[J].Geophysics,2003,68(1):381-385.

[31]Pinnegar C R,Mansinha L.The Bi-gaussian S-transform[J].SIAM Journal of Scientific Computing,2003,24(5):1678-1692.

[32]Kulesh M,Diallo M S,Holschneider M,et al.Polarization Analysis in the Wavelet Domain Based on the Adaptive Covariance Method[J].Goephys J Int,2007,169:1-12.

Adaptive Polarization Analysis and Filtering of Station Seismic Data in Time-Frequency Domain

MA Jian-qing1, LI Qing-chun1, WANG Wei-dong1, WANG Mei-ding2, LI Chun-lan2

(1.SchoolofGeologicalEngineeringandSurveying,Chang’anUniversity,Xi’an710054,Shaanxi，China;2.TeamofGeophysicalandGeochemicalExploration,NorthwesternGeologyExplorationBureauforNonferrousMetalResources,Xi’an710068,Shaanxi，China)

Abstract：Polarization filtering methods based on a covariance matrix play an important role in the processing of multicomponent seismograms due to their explicit physical meaning, ease of implementation, and high efficiency. Conventional polarization filtering methods that are realized in a time domain have major limitations in resolving seismic signals in which waveforms or frequencies overlap. Time-frequency analysis methods are especially suitable for resolving separate seismic signals that overlap in time but have different spectra for instantaneous signal analysis. These methods can describe frequency components of a signal that change over time. Owing to the advantages of the time-frequency analysis method, it can be used in polarization analysis. This study presents a polarization filtering method based on the generalized S-transform to suppress surface waves in a time-frequency domain. On one hand, we remold the window function of the S-transform and improve the frequency resolution of seismic signals by increasing regulatory factors to create a nonlinear change in the window function with the signal frequency. On the other, we structure the cross-energy matrix in the time-frequency domain using the generalized S-transform, compute instantaneous polarization attributes by eigenanalysis, and design a filtering algorithm in the time-frequency domain to achieve polarization filtering of multicomponent seismic signals. The specialties of this method are that the length of the time window of the covariance matrix is determined by the instantaneous frequency of the multicomponent seismic data and it can adapt to the dominant period of the desired signal. Moreover, it calculates polarization parameters at each time-frequency point and no longer needs to perform interpolation. It is particularly accurate in processing signals with overlapping waveforms or frequencies in the time or frequency domain. The results of processing data from models and real three-component seismograms show that this method has very high clarity, high resolution, and practicability in the data analysis and processing of seismograms. This representation enables the detection of dispersion in polarization attributes, which can be further exploited to infer some physical characteristics of the medium under investigation. Moreover, this representation offers the ability to distinguish between attributes that belong to different coherent events that may overlap in time but with different frequency contents separated by time-dependent frequency cutoffs. Identifying and separating different wave types are made possible by designing filters that operate in the time-frequency domain. Attributes such as azimuth, dip, and signed ellipticity can also be used to improve the filtering algorithms.

Key words：polarization filtering; time-frequency analysis; generalized S-transform; adaptive covariance matrix; multi-component seismogram

DOI:10.3969/j.issn.1000-0844.2016.01.0136

中图分类号:P315.63

文献标志码：A

文章编号:1000-0844(2016)01-0136-08

作者简介：马见青(1984-)，男，山西人，博士，讲师,主要从事地震信号多尺度分析和处理研究工作。E-mail：majianqing1984@126.com。通信作者：李庆春(1961-)，男，山东人，教授，博士生导师，主要从事多波多分量地震、金属矿地震偏移成像的研究工作。E-mail：dcliqc@chd.edu.cn。

基金项目：国家自然科学 (41374145)；高等学校博士点 (20120205130002)；中央高校 (310826161008)

收稿日期：①2014-11-20