基于振动台实验的结构损伤识别研究①

王　飞， Reza Shahneam

(1.中国地震局地球物理研究所，北京 100081； 2.北京市地震局，北京100080； 3.美国地质调查局，美国 加州 94025)



基于振动台实验的结构损伤识别研究①

王飞1,2， Reza Shahneam3

(1.中国地震局地球物理研究所，北京 100081； 2.北京市地震局，北京100080； 3.美国地质调查局，美国 加州 94025)

摘要：选择美国加州大学圣地亚哥分校7层钢筋混凝土剪力墙足尺结构振动台实验,开展结构损伤识别研究,实验采用白噪声、环境振动和不同强度的地震动交替激发，记录地震动激发实验前后的结构反应。基于该记录计算和对比自振频率和振型曲率的变化、剪切波走时及其变化和结构层间位移角，分析发现一层和二层振型曲率较大，走时较长，走时变化也较大，现场检查发现一层和二层的破坏也较为严重，这些参数可用于识别结构损伤程度和定位损伤位置，而自振频率和层间位移角变化仅可反映出结构损伤程度，难以揭示结构损伤位置。

关键词：振动台实验; 损伤识别; 模态参数; 等效剪切走时; 层间位移角

0引言

近年来地震摧毁了许多不同类型的建筑结构，因此针对建筑结构的地震反应观测研究逐渐引起地震工程学家的重视，建筑抗震设计规范[1]和许多地方法规[2]要求重大建筑结构安装结构地震反应观测台阵。结构地震反应观测旨在了解和掌握结构体系在强地震作用下的反应性状[3]。一旦获得结构强震反应记录，就相当于对该结构进行了一次原型实验，大量信息可用来揭示结构的抗震性能，这有助于提高结构抗震设计水平，改进抗震设计标准，帮助减轻未来的地震灾害[4]。结构地震反应记录还能通过重建结构地震反应的方式来检验结构地震反应分析中数值模型或实验模型的可靠性[5]。健康建筑结构能有效保障人们生命财产安全，这就需要对结构开展定期安全性能评估，尤其是在遭受破坏性地震后，评估结果可作为结构使用决策的重要依据[6]。然而当前很多工作都集中在基于设计方法的结构抗震能力的理论分析或数值模拟，很少开展基于振动台实验的整体结构抗震性能评价。

基于振动的结构健康监测和损伤识别是以定量方式评估结构安全性能的有效工具。结构健康监测通常采用现场无损探测和系统特性分析方法，通过分析时间域或频率域中系统特性的变化来表明体系存在损伤或者抗震性能退化[7]。本研究调研了过去几十年工程专家们发展的基于振动的结构健康监测和损伤识别方法[8-10]。这些方法中多数仅通过某个结构构件或简单结构体系的数值模拟构建多个损伤情景进行分析验证。由于结构建模中的不确定性和测试结果的简化，这种单纯基于数值模型的分析验证并不充分，需通过实验或实际记录分析验证，如果可能，开展基于破坏性地震中的现场原型实验数据的分析验证将成为检验损伤识别方法的有力工具。尽管当前国内外建成了一些结构地震反应观测台阵，但目前很难获得破坏性地震作用下的数据记录，尚不能用于开展损伤识别的系统研究。因此本工作选择原型破坏性振动台实验来开展结构损伤识别研究。

1损伤识别依据

关于弹性波理论的有关研究表明[11-12]，系统的剪切模量G和系统内剪切波速密切相关，其统计关系为：

其中:ρ为材料密度;vS为等效剪切波速。而弹性模量E和剪切模量G之间的关系为：

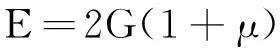
式中:μ为泊松比。

系统刚度K是弹性模量E或剪切模量G与质量惯性矩的乘积，而在经典动力学中，质量惯性矩I只跟刚体形状、刚体自身质量分布和惯性转轴的位置有关，与刚体的转动状态无关。其表达式为：

其中:mi为第i个质量元的质量;ri为第i个质量元到惯性转轴的垂直距离。因此体现系统运动状态的剪切波速vS也直接决定着系统刚度。根据系统自振频率ω:

式中:K表示系统刚度;M表示系统质量。在系统质量保持不变的情况下，系统的等效剪切波速vS、系统刚度K和自振频率ω等特性参数存在正相关性，即体系一旦受到损伤，层间位移角将增大，体系的刚度减小，等效剪切波速和自振频率也相应减小。随着损伤逐渐加重，上述自振特性改变更加显著。因此结构模态参数、剪切波走时和层间位移角可作为结构损伤识别参数用于结构损伤识别。基于上述原理,开展根据振动台试验中的记录数据分析出损伤识别参数的变化,以确定结构损伤的程度和可能位置的深入分析。

2振动台实验

2.1 测试结构概况

建造某足尺的7层结构的薄片进行不同地震输入下的振动测试，该原型测试结构如图1。测试在加州大学圣地亚哥分校的高性能室外振动台上进行。测试的目的在于验证钢筋混凝土墙体的地震反应。

图1　某足尺7层原型测试结构 Fig.1　The 7-story full-scale test structure

该墙体中的横向力由基于位移设计方法获得[9]。承重腹墙是该测试墙体中的主要单元，墙体截面尺寸为3.65 m×0.20 m，可大大提高该测试结构在振动方向的横向刚度。每一层设置矩形楼板，尺寸为8.15 m×3.65 m，腹墙单元和楼板四角处有钢管立柱支撑楼板。一组翼墙和预应力墙为该体系提供了扭转和水平刚度，这两组墙通过开槽和钢支撑跟楼板相连，另外还有横墙用于维持结构在振动实验中的稳定性。该测试结构的总高度约为19.20 m，总重量约为2 450 kN[13]。振动台和测试结构及其周围总共布设139个加速度计，88个位移传感器，314个应变计和23个压力传感器。设置在每一层上的三个加速度计记录结构在振动方向的横向反应，固定在腹墙上的加速度计记录每层中部的反应，楼板处正交于振动方向的两个加速度计记录该方向的相应振动，两个放置在楼板上的加速度计用于记录垂直振动。所有加速度数据的采样频率为240 sps。

2.2测试进程

比对两组临床免疫检验的质量以及真受控率、检验环境等，采用SPSS 18.0统计学软件对数据进行处理，计量资料以“±s”表示，采用t检验，以P＜0.05）为差异有统计学意义。

实验中选择一系列地震动时程和白噪声作为振动方向的振动输入，其中天然地震动时程为1971年圣费南多和1999年北岭的地震记录。在实验过程中地震动输入峰值不断增大，使得结构逐渐产生破坏。两次地震激发振动以后，记录结构的环境振动反应。测试进程的顺序如表1所示。

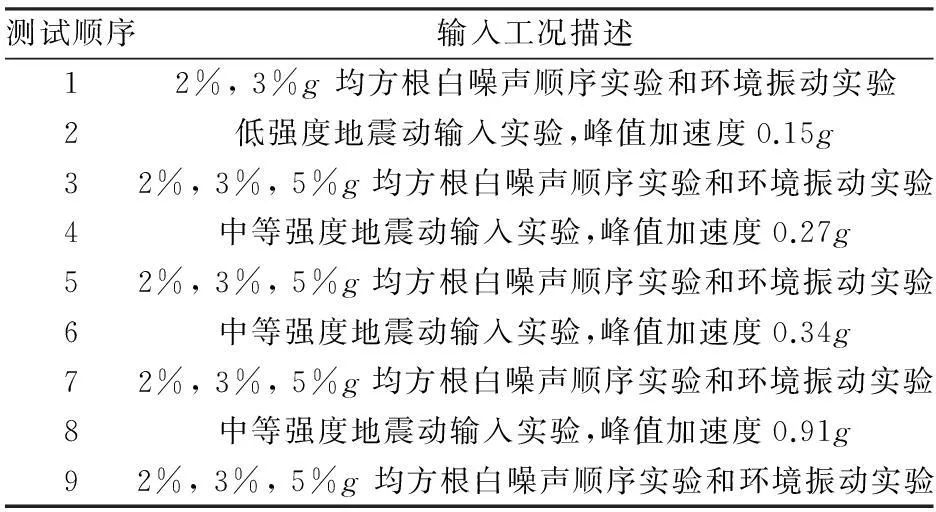
表 1　实验进程的顺序

3测试结果分析

基于上述的实验进程，加速度计记录了全实验过程中的结构反应，这些记录被用于开展结构损伤识别方法分析。通过白噪声实验计算出结构的自振频率和振型，并估算剪切波从该结构基底传播至顶部的时间，而层间位移角则根据四次地震激发实验的结构反应记录数据得出。结构损伤识别参数的变化反映出结构的损伤程度，对于能够用于定位损伤的参数，其变化明显的位置即为结构损伤所在的楼层。

3.1模态参数变化

首先从第一次白噪声测试数据识别出结构的前三阶模态，它们只与无损伤的结构有关，为后续比较提供了一系列的基线值。地震激发实验以后，利用实验后的白噪声数据重复计算结构模态识别参数。规准处理后的频率识别结果列于表2中。随着结构损伤的不断加重,每次地震激发实验后前三阶模态频率估算值逐渐减小。分析表明地震1激发后，结构第一阶模态频率降低9%，结构构件的裂缝不断发展使得结构的有效截面刚度减小[13]。随着裂缝更多更大，结构的有效刚度进一步减小，结构自振特性变化非常明显。地震2和3激发实验后，自振频率规准值减小为66%和74%，直到地震4激发实验后，结构的自振频率规准值减小到49%。此时结构的剩余刚度仅仅只有初始刚度的一半。

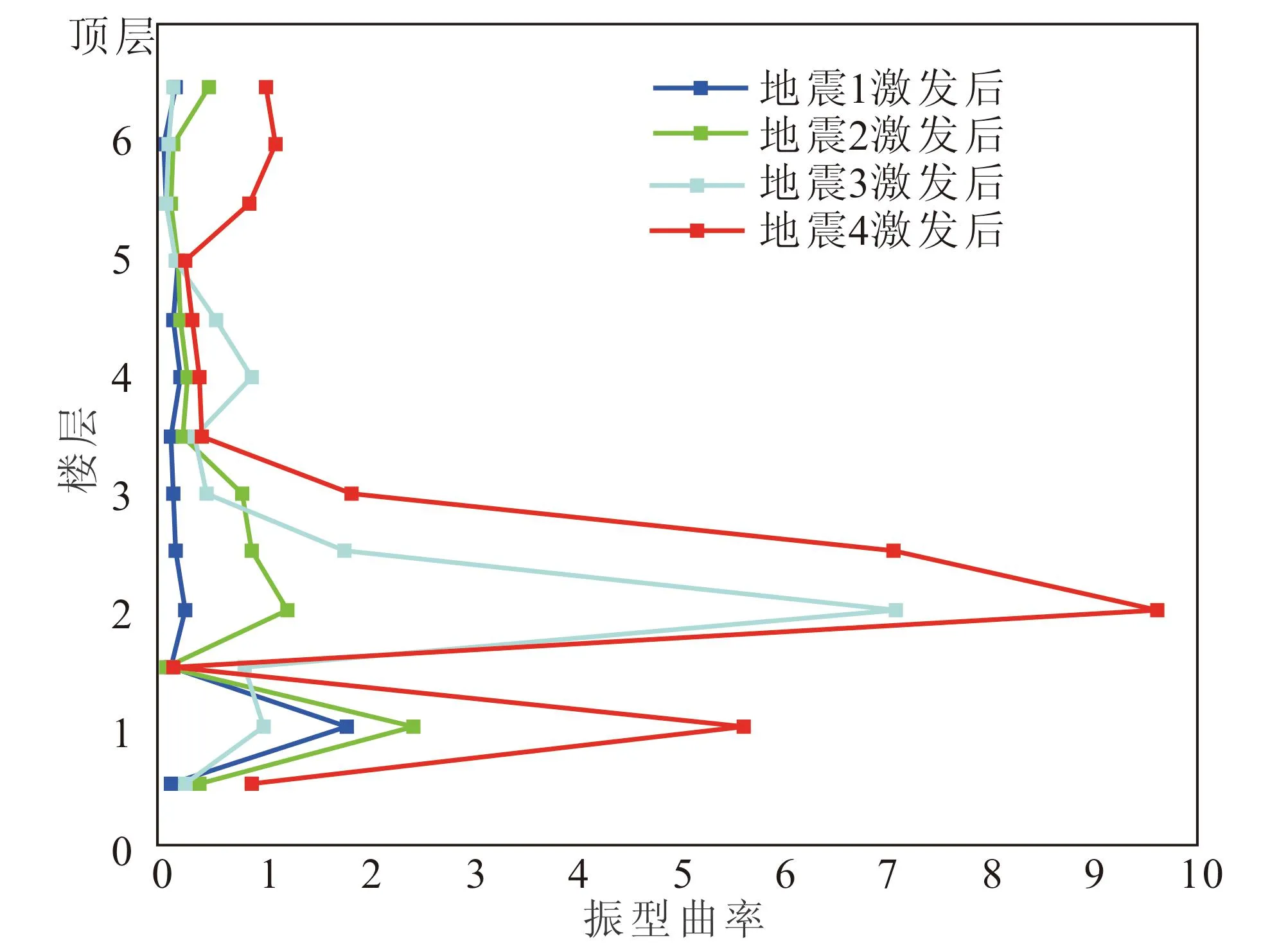
图2　第一阶模态的振型曲率随着地震激发实验　　　 顺序的变化Fig.2　Changes of the modal curvature with different　　　 earthquake test procedure in the first mode

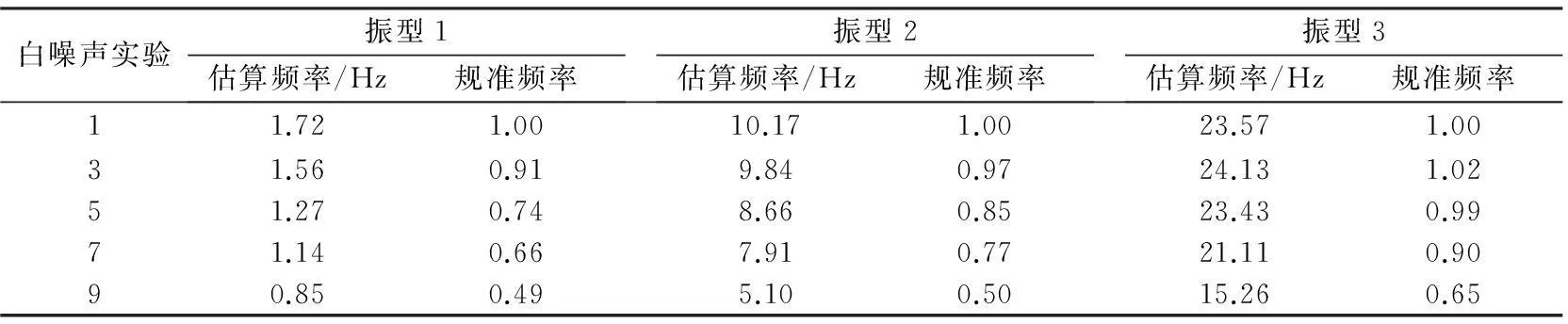
白噪声实验振型1估算频率/Hz规准频率振型2估算频率/Hz规准频率振型3估算频率/Hz规准频率11.721.0010.171.0023.571.0031.560.919.840.9724.131.0251.270.748.660.8523.430.9971.140.667.910.7721.110.9090.850.495.100.5015.260.65

模态分析结果表明自振频率的变化可以作为识别结构是否损伤的有效参数，但不能用来定位结构损伤。本研究采用结构振型曲率来定位结构损伤，以作为主导结构振动的第一阶振型进行振型曲率分析，如图2所示。结果表明，振型曲率的变化率对损伤更敏感，且能够准确地定位损伤的位置。振型曲率的变化主要集中在一层和二层上，变化值详见表3。变化结果与地震激发强度变化规律和现场观测到的损伤程度一致。

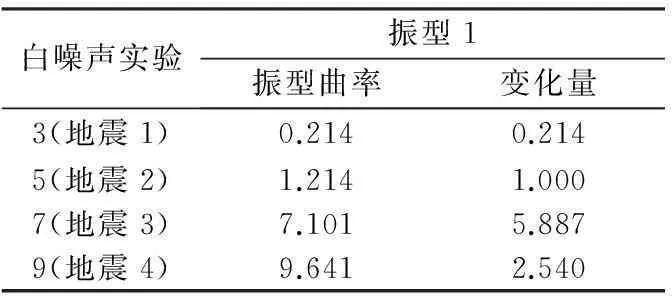
表 3　第一阶振型在第二层处振型曲率变化

3.2剪切波走时

一维波动模型可以用来分析建筑结构的振动特性[14]。通过对不同楼层记录的反卷积分析，可以获得剪切波在结构的走时和平均等效剪切波速。剪切波在结构某楼层中的走时主要取决于该楼层的质量和刚度，因此根据结构中的走时变化也可以识别结构的损伤。结构某位置上的刚度变化使得该楼层上的走时变化，说明结构该位置上存在损伤[15-16]。同样可利用每次地震激发实验后的白噪声数据来计算剪切波走时。本文将所有楼层上的白噪声数据对顶层数据进行反卷积分析，通过12.5 s的移动时间窗来计算走时，如图3(a)所示。

根据反卷积干涉法构建的波场如图3(b)， 波场中显示了各层数据与顶层数据之间的脉冲响应函数。地震波以脉冲方式从一层楼板进入该结构向上传播至顶层，在顶层反射下行并传播至一层。这种具有明显的上行波和下行波的波场可用于计算等效剪切波速。分析表明，通过该时间窗计算出的走时与其他时间窗的计算结果基本一致，因此可基于该时间窗方法计算分层等效剪切波速及其变化。

图3　用于开展反卷积干涉分析和走时计算的白噪　　　声速度时程及时间窗和反卷积干涉波场Fig.3　Velocity time history and time window of the white noise　　　 for the deconvolution analysis and travel-times,calcula-　　　tion and the deconvolved interferometric waveforms

图4　原结构与四次地震激发实验后的地震波绝　　　 对走时及其走时变化Fig.4　The absolute travel-time of seismic wave and its change　　　 before and after the four earthquake excitations

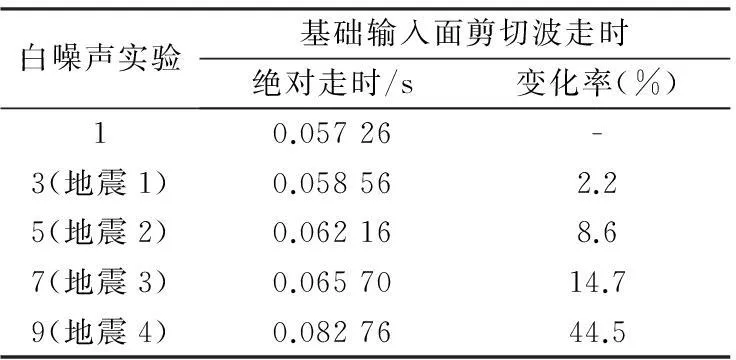
白噪声实验基础输入面剪切波走时绝对走时/s变化率(%)10.05726-3(地震1)0.058562.25(地震2)0.062168.67(地震3)0.0657014.79(地震4)0.0827644.5

在结构遭受地震作用后，不单绝对走时受到影响，走时变化也比较明显[图4(b)]。四次地震激发实验后，走时变化同样表现在底部两层上，其中第1次地震激发实验后基础输入面上的走时变化为0.001 3 s，而在第4次地震激发实验后走时变化为0.025 s，增大为前者的约20倍。由于地震作用水平的不断增加，结构损伤逐渐加重，走时变化同样表现为逐渐增加的趋势。剪切波走时和走时变化同样反映出结构在一二层上损伤较上部各层严重，因此可用走时和走时变化来识别结构的损伤程度并确定结构损伤的位置。

3.3层间位移角

层间位移角是结构设计和抗震性能鉴定中的常用参数。美国联邦法律规定了结构在地震作用下的4种极限状态：可以使用、直接入住、生命安全和防止倒塌。根据FEMA 45014和ASCE 41-615规定，对于测试结构，其直接入住、生命安全和防止倒塌三种极限状态下的瞬态层间位移角限值分别为0.5%、1%和2%，这些限值可直接用于判定结构在地震作用下的损伤状况。本研究中的层间位移角是根据实验中的加速度时程记录,通过基线校正和二次积分获得的层位移时程得到，将相连楼层的层位移时程相减除以对应楼层的高度即可得出该层的层间位移角。取最大层间位移角进行对比分析，4次地震激发后的结构最大层间位移角如图5所示。在第1次地震激发实验后，层间位移角最大值为0.39%，小于0.5%，结构处于直接入住的极限状态下。在第2和第3次地震作用下，层间位移角逐渐增大，除一层外，上部各层全部进入生命安全的极限状态阶段，表明此时该结构不能直接使用，需经过一定的修补或加固后方可使用；结构五层上的层间位移角最大值分别为0.91%和0.96%，接近1%，即将进入防倒塌极限状态。而第4个地震激发实验后，层间位移角全部超过了1%，完全进入防止倒塌的极限状态，最大层间位移角为1.7%，并未超限值2%，结构尚未倒塌。现场检查同样表明第四次地震激发后测试结构遭受了严重损伤，但由于其腹墙的存在使得结构并没有倒塌。分析表明层间位移角也可用于识别结构的损伤程度。

图5　结构不同极限状态下的层间位移角限值和　　　地震激发实验后的结构最大层间位移角Fig.5　Limit values inter-story drift ratio for various　　　 limit states and the maximum ratios after 4　　　 earthquake excitations

4结论和展望

本研究基于美国加州大学圣地亚哥分校的7层钢筋混凝土剪力墙结构的原型振动实验,检验了三种方法的有效性。该实验为基于结构地震反应观测台阵记录的结构损伤识别研究提供了强大的数据库支持和现场检验对比平台。利用结构上安装的结构地震反应观测设备获得结构反应记录分析结构的模态参数、剪切波走时和层间位移角等参数，并利用其变化来综合判定结构损伤程度及其损伤位置，损伤识别的结果和实验数据的对比表明定性的结构损伤描述与损伤识别方法给出的定量结果相同，分析表明上述参数可用于开展结构损伤识别分析，并设定了对应于不同损伤状态下的损伤识别参数的阈值。下一步将挖掘更多的结构损伤识别参数并检验各阈值的合理性，确定更准确的结构损伤阈值，以此推进结构地震反应观测台阵的工程应用，为结构抗震设计和建筑结构的抗震性能鉴定等工作提供参考。

致谢:感谢Ulusoy Hasan为本研究中使用的损伤识别方法提供的指导和帮助，同时也感谢Babak Moaveni为本研究提供的振动台实验数据。

参考文献(References)

[1]GB50011-2010，建筑抗震设计规范[S].北京：中国建筑工业出版社, 2010.

GB50011-2010，Code for Seismic Design of Buildings[S].Beijing: Building Industry Press of China, 2010. (in Chinese)

[2]北京市地震局. 北京市实施《中华人民共和国防震减灾法》规定[S].北京, 2013.

Earthquake Administration of Beijing Municipality.Provisions for Implementing Law of China on Protecting Against and Mitigating Earthquake Disasters[S].Beijing,2013. (in Chinese)

[3]谢礼立,于双久.强震观测与分析原理[M].北京:地震出版社,1982.

XIE Li-li,YU Shuang-jiu.Strong Motion Observation and Analyzing Theory[M].Beijing: Seismological Press,1982. (in Chinese)

[4]李鸿晶,朱士云, Mehmet C.强震观测建筑结构的地震反应分析[J].地震工程与工程振动,2003,23(6): 31-36.

LI Hong-jing,ZHU Shi-yun, Mehmet C.Seismic Response Analysis of an Instrumented Building Structure[J].Earthquake Engineering and Engineering Vibration,2003,23(6):31-36.(in Chinese)

[5]Mehmet C. Current Practice and Guidelines for USGS Instrumentation of Buildings Including Federal Buildings[R]//Prepared for 2001 Workshop on Structural Instrumentation for Consortium of Organizations for Strong-motion Observation Systems.2001.

[6]郑山锁,田进,韩言召,等.考虑锈蚀的钢结构地震易损性分析[J].地震工程学报,2014,36(1):1-6.

ZHENG Shan-suo,TIAN Jin, HAN Yan-zhao,et al.Steel Structure Seismic Vulnerability Analysis Considering Steel Corrosion[J].China Earthquake Engineering Journal,2014,36(1):1-6. (in Chinese)

[7]郑山锁,代旷宇,孙龙飞,等.钢框架结构的地震损伤研究[J].地震工程学报,2015,37(2):290-297.

ZHENG Shan-suo,DAI Kuang-yu,SUN Long-fei,et al.Research on the Seismic Damage of Steel Frame Structure[J].China Earthquake Engineering Journal,2015,37(2):290-297. (in Chinese)

[8]Carden E P,Fanning P.Vibration Based Condition Monitoring: A Review[J].Structural Health Monitoring,2004,3(4):355-377.

[9]Doebling S W,Farrar C R,Prime M B,et al.Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: a Literature Review[R].Los Alamos National Laboratory,Los Alamos,NM,1996.

[10]Sohn H,Farrar C R,Hemez F M,et al.A Review of Structural Health Monitoring Literature:1996-2001[R].Los Alamos National Laboratory,Los Alamos,NM,2003.

[11]Schneider J A,Hoyos L,Mayne P W,et al.Field and laboratory Measurements of Dynamic Shear Modulus of Piedmont Residual Soils[C]//Behavioral Characteristics of Residual Soils,GSP92,American Society of Civil Engineers,Reston,VA.1999.

[12]Suleyman K,Yalcin M.A Simple Soil-structure Interaction Model[J].Applied Mathematical Modelling,2000,24:607-635.

[13]Panagiotou M,Restrepo J I,Conte J P.Shake-table Test of 7-Story Building Slice. Phase I:Rectangular Wall[J].Journal of Structural Engineering,2011,137(6):691-704.

[14]Snieder R,Safak E.Extracting the Building Response Using Seismic Interferometry:Theory and Application to the Millikan Library in Pasadena, California[J].Bulletin of the Seismological Society of America,2006,96(2):586-598.

[15]Todorovska M I,Trifunac M D.Impulse Response Analysis of the Van Nuys 7-story Hotel during 11 Earthquakes and Earthquake Damage Identification[J].Structural Control and Health Monitoring,2008,15(1):90-116.

[16]Todorovska M I,Trifunac M D.Earthquake Damage Identification in the Imperial County Services Building-I:The Data and Time-frequency Analysis[J].Soil Dynamics and Earthquake Engineering,2007,27(6):564-576.

Structural Damage Identification Based on Shaking Table Tests

WANG Fei1, 2, REZA Shahneam3

(1.InstituteofGeophysics,CEA,Beijing100081,China;2.EarthquakeAdministrationofBeijingMunicipalityBeijing100080,China; 3.U.S.GeologicalSurvey,California94025,USA)

Abstract：In this study, we chose high-performance shaking-table tests of a full-scale seven-story reinforced-concrete shear wall structure at the University of California, San Diego to test this method with respect to damage identification. We alternately tested the structure under the excitations of white noise, the environment, and nine earthquakes. For each case, we scaled the amplitudes of the input ground motions to various levels. We recorded the acceleration responses before and after the earthquake excitations with seismometers located on the seven floors. We determined the vibration characteristics for each earthquake excitation by analyzing the acceleration responses mentioned above. These characteristics include the modal information, the shear-wave propagation characteristics, and the inter-story drift ratio. We estimated the modal frequencies of the first three modes from the recordings when white noise was first applied to the building, and considered these as the criterion. The subsequent modal frequencies were then normalized and compared with this criterion. The normalized frequencies diminished gradually with the load case tests and the normalized frequency reduced by 51 percent for the first mode. The reduction in the modal characteristics indicates that crevices develop as the amplitude of the input ground motions increase, and thereby decrease the rigidity. Lower rigidity suggests that damage throughout the building has been aggravated. However, changes in modal frequencies cannot be used to locate damage. Mode shape curvatures of the building were similarly applied to identify the building damage. Test results demonstrate that the mode shape curvatures increase significantly with the test process and the main changes were concentrated on the second floor. After the excitations of earthquakes 1, 2, 3, and 4, the curvature values were 0.214, 1.214, 7.101, and 9.641, respectively. Therefore, we conclude that the damage on the second floor was more severe. Subsequently, we used a one-dimensional shear-wave propagation model to form the virtual waveform by deconvolving the recordings on each floor with the signal on the seventh floor. This waveform has a wave equation that is identical with that of a physical waveform and reflects the propagation characteristics of the shear wave in the building. Upward traveling and downward traveling waves are recognized in the virtual waveform. The travel time of the shear waves is inferred from the upward and downward traveling waves. At the same time, we obtained the changes in the travel time. The travel time and its changes both increase with the amplitude of the input ground motions. The travel change after the earthquake-4 excitation rose by 44.5 percent on the first floor. The travel time and its changes suggest that the lower two floors were more damaged than the upper floors, and are appropriate for damage identification as well. Finally, we computed the inter-story drift ratio and compared the results with the response after the excitations of the four earthquakes. The inter-story drift ratio increases after the input ground motions and breaks through the limit values of immediate occupancy of 0.5 percent and life safety of 1.0 percent for a reinforced concrete building. After excitation by earthquake 4, the drift ratio approaches the limit value of collapse prevention of 2.0 percent. Our analysis indicates that the parameters described above are sufficient to identify the damage.

Key words：shaking table test; damage identification; modal parameters; equivalent travel time of shear wave; inter-story drift ratio

DOI:10.3969/j.issn.1000-0844.2016.01.0129

中图分类号:TU317

文献标志码：A

文章编号:1000-0844(2016)01-0129-07

作者简介：王飞(1979-)，男，副研究员，硕士，主要从事结构地震反应观测研究。E-mail: wangfei@bjseis.gov.cn。

基金项目：中国地震局青年科技骨干人才项目(201204190030)

收稿日期：①2015-01-05