全非平稳地震作用的结构随机反应与可靠度分析①

吴林强， 王　舟， 刘章军

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.三峡大学 土木与建筑学院，湖北 宜昌 443002)



全非平稳地震作用的结构随机反应与可靠度分析①

吴林强1， 王舟1， 刘章军2

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.三峡大学 土木与建筑学院，湖北 宜昌 443002)

摘要：在平稳地震动过程的Clough-Penzien功率谱基础上，采用林家浩非均匀调制函数建立全非平稳地震动过程的演变功率谱。根据我国现行的《建筑抗震设计规范》进行全非平稳地震动演变功率谱的参数识别研究。应用非平稳随机过程模拟的谱表示-随机函数方法，生成建筑结构抗震设计所用地震动的代表性样本集合。通过代表性样本集合的二阶统计值及地震反应谱与目标值的拟合比较，验证本文方法的有效性。最后结合概率密度演化方法，进行以层间位移角为控制准则的结构随机地震反应分析与抗震可靠度计算。

关键词：地震动； 全非平稳； 概率密度演化方法； 结构； 随机反应； 可靠度

0引言

地震地面运动具有很强的随机性，目前工程抗震中广泛使用的地震动输入模型大多是强度非平稳地震动过程，不能反映地震动的频率非平稳特性。如何生成具有强度和频率全非平稳的地震动加速度过程，一直是地震动随机模型研究的难点和热点。目前模拟强度和频率非平稳过程的主要方法有谱表示、小波分析、Hilbert-Huang变换和Wigner-Ville分布等。在谱表示方法中，Shinozuka等[1]利用三角级数法和演变功率谱模拟非平稳地震动过程；Liang等[2]根据演变谱理论导出了非平稳地震动过程模拟的一个谱表示方法；张翠然等[3]基于Priestley演变谱理论，提出拟合目标演变谱生成强度和频率全非平稳地震动时程的迭代方法。谱表示法理论完善、算法简单，但计算工作量大。小波分析通过一系列可伸缩和平移的小波基函数，从而达到对信号时频局部化分析的目的[4]。但小波基函数限定的长度会造成信号的能量泄漏，因而难以对信号作精确的时频分析。Hilbert-Huang变换[5]建立在经验模态分解和Hilbert谱分析基础上，具有清晰的物理意义，但其端点数据发散效应尚未解决。Wigner-Ville分布[6]通过瞬时谱能够将地震动的能量分布表示在联合的时域中进行人工地震动的合成，但它最主要的缺陷是交叉干扰的存在和在某些频段内有负的能量。如何合理、有效地描述强度和频率全非平稳地震动过程，并从代表性样本集合的角度研究地震动随机过程，是目前工程随机动力学研究的一个新途径。

本文拟采用林家浩提出的指数衰减型非均匀调制函数[7-8]，结合平稳地震动过程的Clough-Penzien功率谱模型[9]，建立强度和频率全非平稳地震动过程的演变功率谱模型，并根据我国现行的《建筑抗震设计规范》(GB50011-2010)[10]，进行演变功率谱模型的参数识别研究；同时采用文献[11]非平稳地震动过程模拟的谱表示-随机函数方法，生成建筑结构抗震设计所用地震输入的代表性样本集合；最后应用该方法生成的代表性样本集合;结合最近的概率密度演化方法[12-13]，进行一个框架结构随机地震反应实例分析与抗震可靠度计算。

1非平稳过程的谱表示-随机函数方法

根据大量的地震记录统计，地震动的均值为零，因此设零均值的非平稳地震动加速度过程为Xg(t)，则非平稳地震动加速度过程模拟的谱表示[11]：

式中：ωk=kΔω,Δω为离散的频率步长；N为截断项数；SXg(t,ω)为双边的演变功率谱密度函数，满足SXg(t,ω0)=SXg(t,0)=0的条件。

在式(1)中，Xk与Yk(k=1,2,…,N)为标准正交随机变量，即：

(2)

式中：E[·] 表示数学期望；δjk为Kronecker-delta记号。

式(1)由于截断项数N而引起的均方相对误差为：

(3)

式中：ωu=NΔω为截断频率；T为地震动过程的持续时间。

(4)

2非平稳地震动概率模型的建立

2.1演变功率谱

在平稳地震动随机过程模型中，金井清谱[15]考虑了地表土层特性对地震动频谱特征的影响，具有明确的物理意义，是目前地震工程中应用较为广泛的地震动随机模型。然而金井清谱也夸大了地震地面运动的低频含量，不能反映基岩地震动的频谱特性,同时在零频处不满足位移和速度是有界的条件。为此，许多学者对金井清谱进行了修正。本文选用Clough和Penzien提出的双过滤白噪声模型[9]，其功率谱密度函数为：

(5)

式中:ωf、ξf分别为第二过滤层的卓越圆频率和阻尼比，文献[16]建议取ωf=0.1ωg，ξf=ξg；ωg、ξg分别为地表土的卓越圆频率和阻尼比，一般ωg可按ωg=2π/Tg计算，其中Tg为规范的特征周期,ξg可采用文献[16]建议的取值；S0为谱强度因子，反映地震动强弱程度，可表示为[11]：

(6)

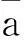
对于全非平稳地震动随机过程模型，其非平稳主要表现在地震动强度和频率特性都随时间发生变化。全非平稳地震动过程的演变功率谱一般可表示为：

(7)

其中:S(ω)是平稳地震动过程的功率谱密度函数，如式(5)所示;A(t,ω)为非均匀调制函数，本文选取林家浩提出的指数衰减型非均匀调制函数[7]：

(8)

式中:U(t,ω)为指数衰减型调制函数;ωa和ta是为了将ω和t分别无量纲化而引入的频率与时间参数，原则上可以任选，本文建议ωa=ωg，ta=T，其中T为地震动过程的持续时间。

根据文献[8]可知，η0越大高频成分就衰减越快，当η0=0，即U(t,ω)=1，调制函数就退化为均匀调制情况。因此，可将η0称作调频因子，将U(t,ω)称作调频函数，而将g(t)称作调幅函数，当然U(t,ω)也起一些调幅作用。调幅函数g(t)建议选取[17]：

(9)

其中:c为随机地震动峰值加速度出现的大致时间;d是控制A(t,ω)形状的指数。

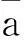
表 1　演变功率谱模型参数

注：圆频率单位1/s =rad/s。

图1给出了双边的演变功率谱密度函数随时间t和频率ω的变化关系。由于演变功率谱关于频率ω对称，图中仅画出了频率ω≥0的部分。可以看到，演变功率谱的峰值出现在10 s左右，能量主要集中在40 rad/s频率以内。

图1　演变功率谱密度函数Fig.1　Evolutionary power spectral density function

2.2地震动代表性样本集合的生成

为了生成非平稳地震动加速度过程的代表性样本集合。首先，应用华罗庚-王元的数论方法[18]对均匀分布的基本随机变量Θ1和Θ2在区间[0,2π)×[0,2π)上选取代表点，其中代表点的总数s=152;其次，应用随机函数的表达式(4)以及标准正交随机变量的确定性映射方式，得到式(1)所需的标准正交随机变量;最后，应用非平稳随机过程模拟的谱表示式(1)，即可生成152条地震动代表性样本的集合。在非平稳地震动加速度过程模拟的谱表示中，参数ωu=240 rad/s，N=1 600，Δω=0.15 rad/s。根据式(3)，场地类别为Ⅲ，设计地震分组为第二组的均方相对误差ε(N)=0.23%。同时，地震动持续时间T=30 s，时间间隔Δt=0.01 s，满足Δt≤π/ωu的条件。

图2给出了非平稳地震动加速度过程的典型代表性样本。由图可见，代表性样本具有由弱到强的初始阶段、持续的强震阶段和由强到弱的衰减阶段，反映了地震动的强度非平稳性。同时样本时程还具有疏密不均的特性，开始阶段高频成分较多，随后低频成分逐渐增多，反映了地震动的频率非平稳特性。

图2　非平稳地震动加速度过程的代表性样本Fig.2　Generated representative sample function of　　　 nonstationary ground motion acceleration process

图3为152条代表性样本的均值、标准差与目标均值、目标标准差的比较。从图中可知，在二阶统计特性意义上，152条代表性样本的总体特性与目标值符合较好。图4给出了152条代表性样本的均值反应谱曲线与规范反应谱曲线的比较。从图可见，均值反应谱与规范反应谱除在长周期部分(大于3 s)有一定误差外，在其他周期部分的拟合程度较好。

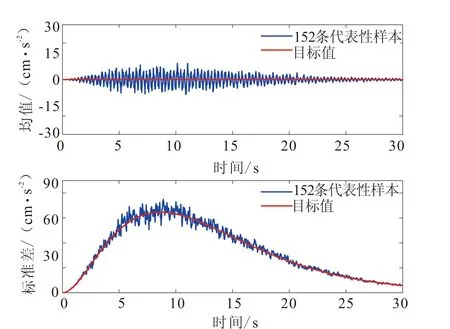
图3　样本总体的均值、标准差与目标值的比较Fig.3　Comparison between mean and deviation from 152　　　 samples ensemble and from the target

图4　样本总体的反应谱与规范反应谱的比较Fig.4　Comparison between 152 samples ensemble’s response　　　　 spectrum and the code's response spectrum

3实例分析

近年来，概率密度演化理论在线性与非线性结构随机动力反应分析、动力可靠度方面取得了一系列的研究进展[12-13]。应用全非平稳地震动过程的谱表示-随机函数方法生成的代表性样本集合与概率密度演化理论相结合，可以实现工程结构的随机地震反应分析与抗震可靠度计算[19]。

为了简要说明本文建立的全非平稳地震动概率模型的应用，以某三层钢筋混凝土结构为例(图5)，其主要结构类型为梁板柱结构。沿X方向的跨度为6 m，沿Z方向为2跨3柱，跨距均为5 m，每层层高均为4 m。楼板和屋盖厚度为200 mm，框架主截面为0.5 m×0.5 m，横梁截面为0.3 m×0.6 m。材料力学特性为：弹性模量为30 GPa，泊松比为0.1667，密度为2 500 kg/m3。本文采用通用有限元软件ANSYS建立其结构空间有限元模型，混凝土采用SOLID185单元，其中共有9 971个单元，2817个节点。

图5　三层框架有限元模型Fig.5　Finite element model of the three-story frame

在对有限元模型进行模态分析时，为提高结构的自振频率和振型的计算精度，本文采用Lanczos法进行模态分析。限于篇幅，表2仅列出部分振动频率及相应振型特点。由表2可知，该框架结构的基频为5.841 Hz，在X向振动以第1振型为主，在Z向振动以第2振型为主。另根据模态计算相关数据，结构在X、Y、Z向主振型的有效参与质量比例为1∶0∶1,即参与Y方向(竖向)振动的结构质量几乎为0，这说明钢结构振动以水平向为主。

表 2　动力特性分析结果

应用本文方法生成的152条代表性样本，沿X方向输入。结合最近的概率密度演化方法(PDEM)，分别计算上述结构各层层间位移角的随机地震反应，进而计算各层的动力可靠度。限于篇幅，本文仅给出第二层层间位移角反应的概率信息图形，如图6所示。图6(a)为按照概率密度演化方法计算给出的该结构第二层层间位移角反应均值和标准差；图6(b)为典型时刻的概率密度函数；图6(c)为给定时间段内的概率密度演化曲面；图6(d)为相应的等概率密度线。图6中可见，结构反应的概率密度具有典型的演化特征，概率密度分布是非规则曲线，具有随机涨落现象，与一般假定的正态分布等规则分布明显不同。

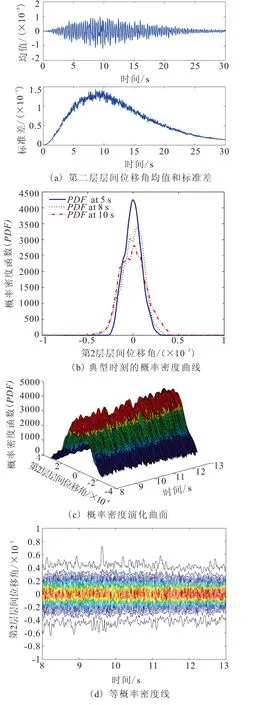
图6　第二层层间位移角反应的概率信息Fig.6　Probability information by story displacement　　　 angle of the second story

基于等价极值事件的体系可靠度分析方法[20]，以层间位移角为控制准则，给出了三层框架结构的每一层抗震可靠度，如图7所示。事实上，层间位移角的等价极值事件的分布函数(纵坐标)即为抗震可靠度，可以看出，第二层的抗震可靠度最低。若层间位移角的界限值给定为1/2 500，第一层和第三层的抗震可靠度接近100%，而第二层的抗震可靠度只有84%。

图7　等价极值事件的结构抗震可靠度Fig.7　Seismic reliability of the structure based on　　　 the equivalent extreme-value event

4结语

本文建立了一类全非平稳地震动加速度过程的概率模型及建筑结构抗震设计所用地震动的代表性样本集合。同时，结合概率密度演化方法进行了结构随机地震反应与抗震可靠性分析。主要结论如下：(1)本文建立的全非平稳地震动概率模型较全面地考虑了地震动的非平稳特性、频谱特性和时域特性；(2)全非平稳地震动过程的概率模型能够在代表性样本集合的二阶统计值以及地震反应谱等方面与目标值(谱)相一致，从而在代表性样本集合的层面上研究地震动过程的概率特性；(3)全非平稳地震动过程的概率模型能够方便地与最新发展的概率密度演化理论(PDEM)相结合，为实现复杂工程结构的随机地震反应和抗震可靠性的精细化分析提供了新途径。

参考文献(References)

[1]Shinozuka M,Jan C M.Digital Simulation of Random Processes and Its Applications[J].Journal of Sound and Vibration,1972,25(1):111-128.

[2]Liang J W,Chaudhuri S R,Shinozuka M.Simulation of Nonstationary Stochastic Processes by Spectral Representation[J].Journal of Engineering Mechanics,2007,133(6):616-627.

[3]张翠然,陈厚群.基于渐进谱的幅值和频率非平稳人造地震动拟合[J].地震工程与工程振动,2008,28(3):24-32.

ZHANG Cui-ran,CHEN Hou-qun. Prediction of Non-stationary Earthquake Accelerograms Compatible with Design Evolutionary Spectra[J].Earthquake Engineering and Engineering Vibration,2008,28(3):24-32. (in Chinese)

[4]Mallat M.Multiresolution Approximation and Wavelets[J].Transaction of America Mathematics Society,1989,315:69-88.

[5]Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proc R Soc Lond,1998,454:903-995.

[6]Mark W D.Spectral Analysis of the Convolution and Filtering of Non-stationary Stochastic Process[J].Journal of Sound and Vibration,1970,11(1):19-63.

[7]林家浩,张亚辉,孙东科,等.受非均匀调制演变随机激励结构响应快速精确计算[J].计算力学学报,1997,14(1):2-8.

LIN Jia-hao,ZHANG Ya-hui,SUN Dong-ke,et al.Fast and Precise Computation of Structural Responses to Non-uniformly Modulated Evolutionary Random Excitations[J].Chinese Journal of Computational Mechanics,1997,14(1):2-8. (in Chinese)

[8]张亚辉,林家浩.多点非均匀调制演变随机激励下结构地震响应[J].力学学报,2001,33(1)：87-95.

ZHANG Ya-hui,LIN Jia-hao.Seimic Responses of Structures Subjected to Non-uniformly Modulated Differential Evolutionary Random Excitations[J].Acta Mechanica Sinica,2001,33(1):87-95. (in Chinese)

[9]Clough R W,Penzien J.Dynamics of Structures[M].New York:McGraw-Hill,Inc,1993.

[10]中华人民共和国住房和城乡建设部.GB50011-2010,建筑抗震设计规范[S]. 北京:中国建筑工业出版社,2010.

Ministry of Housing and Urban-rural Development of the People’s Republic of China. GB50011-2010,Code for Seismic Design of Buildings[S].Beijing:China Architecture & Building Press,2010. (in Chinese)

[11]刘章军,曾波,吴林强.非平稳地震动过程模拟的谱表示-随机函数方法[J].振动工程学报,2015,28(3):411-417.

LIU Zhang-Jun,ZENG Bo,WU Lin-qiang.Simulation of Non-stationary Ground Motion by Spectral Representation and Random Functions[J].Journal of Vibration Engineering, 2015,28(3):411-417. (in Chinese)

[12]LI Jie,CHEN Jian-bing.Stochastic Dynamics of Structures[M].John Wiley & Sons,2009.

[13]李杰,陈建兵.随机动力系统中的概率密度演化方程及其研究进展[J].力学进展, 2010,40(2):170-188.

LI Jie,CHEN Jian-bing.Advances in the Research on Probability Density Evolution Equations of Stochastic Dynamical Systems[J].Advances in Mechanics,2010,40(2):170-188. (in Chinese)

[14]刘章军,方兴.平稳地震动过程的随机函数-谱表示模拟[J].振动与冲击,2013,32(24):6-10.

LIU Zhang-jun,FANG Xing.Simulation of Stationary Ground Motion with Random Functions and Spectral Representation[J].Journal of Vibration and Shock,2013,32(24): 6-10. (in Chinese)

[15]Kanai K.An Empirical Formula for the Spectrum of Strong Earthquake Motions[J].Bull Earthquake Res Inst Univ Tokyo,1961,39:85-95.

[16]薛素铎,王雪生,曹资.基于新抗震规范的地震动随机模型参数研究[J].土木工程学报,2003,36(5):5-10.

XUE Su-duo,WANG Xue-sheng,CAO Zi.Parameters Study on Seismic Random Model Based on the New Seismic Code[J].China Civil Engineering Journal,2003,36(5):5-10. (in Chinese)

[17]欧进萍,王光远.结构随机振动[M].北京:高等教育出版社,1998.

OU Jin-ping,WANG Guang-yuan.Random Vibration of Structures[M].Beijing:Higher Education Press,1998. (in Chinese)

[18]Li J, Chen JB.The Number Theoretical Method in Response Analysis of Nonlinear Stochastic Structures[J].Computational Mechanics,2007,39(6):693-708.

[19]曾波,邢彦富,刘章军.基于概率密度演化的渡槽结构抗震分析[J].地震工程学报,2014,36(4):991-996.

ZENG Bo,XING Yan-fu,LIU Zhang-jun.Seismic Analysis of Large-scale Aqueduct Structures Based on the Probability Density Evolution Method[J].China Earthquake Engineering Journal,2014,36(4):51-55. (in Chinese)

[20]Li J,Chen J B,Fan W L.The Equivalent Extreme-value Event and Evaluation of the Structural System Reliability[J].Structural Safety,2007,29(2):112-131.

Stochastic Responses and Reliability Analysis of Structures Subjected to Fully Nonstationary Ground Motion

WU Lin-qiang1, WANG Zhou1, LIU Zhang-jun2

(1.CollegeofHydraulic&EnvironmentalEngineering,ChinaThreeGorgesUniversity,Yichang443002,Hubei,China;2.CollegeofCivilEngineering&Architecture,ChinaThreeGorgesUniversity,Yichang443002,Hubei,China)

Abstract:This paper proposes a new probability model for the fully nonstationary ground motion acceleration process, and provides a kind of seismic input for structures for use in seismic research. First, based on the Clough-Penzien power spectrum of the stationary ground motion process, we establish the evolutionary power spectrum of the fully nonstationary ground motion process. Most importantly, the evolutionary power spectrum considers not only the nonstationary intensity, but also the nonstationary frequency. Then, based on the seismic design building code (in China), we identify these parameters in the evolutionary power spectrum model for different site conditions. Meanwhile, we applied the spectral representation-random functions method to generate an ensemble of 152 representative samples, and assigned each representative sample a given probability. This method uses a few basic random variables to express the original seismic ground motion process. Next, we obtain second-order statistics and the seismic response spectrum of the representative sample ensemble, and compare them with the target values. The results show that the general characteristics of all 152 representative samples coincide well with the target values. In this study, to verify the superiority and effectiveness of the proposed method, we used ANASYS software to conduct a dynamic time-history analysis of a concrete framework. Finally, by combining the recent probability density evolution method with the control criteria for the displacement angle, we performed a stochastic dynamic response analysis and reliability calculation for the concrete framework.

Key words：ground motion; fully nonstationary; probability density evolution method; structure; stochastic response; reliability

DOI:10.3969/j.issn.1000-0844.2016.04.0109

中图分类号:O324；TU311.3

文献标志码：A

文章编号:1000-0844(2016)01-0109-07

作者简介：吴林强(1990-)，男，硕士研究生，主要从事工程结构抗震研究。E-mail:wulinqiang123@sina.com。通信作者：刘章军(1973-)，男，博士，教授，博士生导师，主要从事工程结构抗震研究。E-mail:liuzhangjun73@aliyun.com。

基金项目：国家自然科学 (51278282，50808113)

收稿日期：①2015-01-19