工程实验极限测试数据的二次拟合推演研究
2016-04-07董小微徐方超
孙 凤,董小微,徐方超
(沈阳工业大学 机械工程学院,辽宁 沈阳,110870)
工程实验极限测试数据的二次拟合推演研究
孙 凤,董小微,徐方超
(沈阳工业大学 机械工程学院,辽宁 沈阳,110870)
在工程实验中,由于实验条件有限,极限条件下的关键实验数据无法获得。针对此类问题,提出一种基于已测实验数据的极限条件实验数据推理方法,根据已有数据规律,采用二次参数拟合法推理极限条件下数据模型,获得极限条件下的推演数据。推演实例表明,该极限条件数据推演方法有效,可行。
数学推理;函数模型;推演方法;二次参数拟合
0 前言
数学推理包括演绎推理、合情推理及实践性推理等,但其本质在于演绎推理[1,2]。在如今工程实验的实验过程中,常会遇到数据处理过于繁琐的问题,而造成这种现象的原因有很多,例如仪器不稳定,一些实验中测量数据会发生仪器不稳定的现象,导致测量结果误差偏大并且有些数据需反复测量多次[3]。有些系统仪器精密度较高,但是其系统方程具有高维及非线性的特点,仅依靠数值方法难以满足分析与设计要求[4]。还有一些系统的处理方法过于复杂,例如利用软件建立的模型特征过多或者结构过于复杂[5,6,7];一些传统的数学分析方法对于复杂的高噪声、强干扰信号进行瞬时频率估计的结果往往偏离真实值误差较大[8]。但是其中最让人困扰的莫过于由于仪器的精度和稳定性有限,实验室中的仪器是测不出极限条件下的关键数据的。有时根据数学模型的不同,需要设计不同的解决方法[9,10],其过程过于复杂。实际测试实验中,不允许实验仪器接近极限条件,以免损坏器械。
针对此类现象,本文提出一种推理方法,该方法借鉴了一种有效的推理技术(CBR)的中心思想[11],摒弃了一些数据推理分析方法存在的计算复杂,不能进行反向推理等不足[12],该方法可根据同一个实验中已测数据推演出极限条件下的一系列关键数据并进行仿真分析。经实验验证,该数据推理方法简单、有效。
1 推理方法提出
在工程实验中,由于实验条件有限,已知一组或多组实验数据,却无法由实验仪器精确测出极限条件下的关键实验数据。遇到此类情况,可以通过如下方法解决:
根据已知实验数据建立相应的数学模型如下
y(x)=anxn+an-1xn-1+…+ax+b
(1)
该数学模型可根据实际需要进行适当的改变。对数学模型进行参数的拟合并从中找出参数间的规律。二次参数拟合的数学模型如下
(2)
从上述公式中得出的规律对参数进行拟合;最后,建立极限条件下的数据模型,并与已知的实验数据进行对比分析。其总体流程如下图所示

图1 二次参数拟合推演方法流程图Fig.1 Flow chart of secondary parameter fitting deduction method
2 推演实例
2.1 已知实验数据
在某永磁悬浮力的测量实验中,在实验装置的有效使用范围及传感器的测量范围内,获得如图2所示实验结果。其中横坐标为永磁铁回转角度,纵坐标为某永磁悬浮装置的悬浮力,每一条曲线代表不同悬浮气隙下的系统的悬浮力,悬浮气隙的变化范围在2~8 mm。

图2 工程实验结果Fig.2 Result of engineering experiment
但是由于研究需要,需要得知悬浮间隙为1 mm与9 mm时,该永磁悬浮系统的悬浮力的基本实验数据,虽然根据以上实验结果大致可以推测出D=1 mm与D=9 mm时,曲线仍近似为正弦曲线,但其实际峰值与振幅并不能知晓。而此气隙为实验装置的极限范围,无法获取相应数据,这时就需要根据已有的实验数据进行分析对比,获取所需数据。
2.2 数据模型建立及参数拟合
首先,需建立已有数据的数学模型,以图2所示气隙为2 mm时的悬浮力数据为例,建立其数学模型。采用相应数据处理软件拟合实验数据并获取拟合数学模型如下:
f2=3.195sin(0.00111x+1.36)+
3.057sin(0.3481x-1.512)
(3)
根据上述方法可以得出从2 mm~8 mm的七条正弦曲线的公式,并拟合出参数规律图(图3)。从图3中各参数规律可以看出,系数a1、a2是按一定规律从2 mm到8 mm递减的,b1、b2几乎不变,c1、c2稳定在一个极小的范围内。
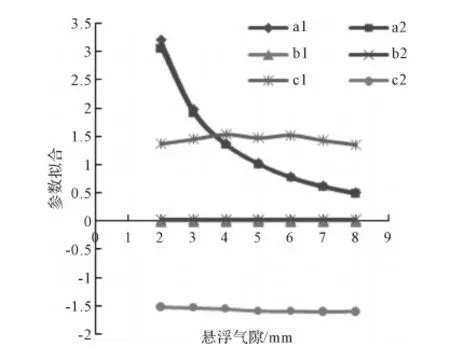
图3 模型参数规律图Fig.3 Rule of the model parameter
根据以上数据,用数据处理软件对参数a1、a2进行拟合可以得出a1、a2的数学模型如式(4)、式(5)所示:
a1(x)=7.313x-1.075-0.2732
(4)
a2(x)=6.823x-0.9809-0.4027
(5)
2.3 极限条件数据获取与对比分析
根据2.2中所述数学模型(4)、(5),带入极限条件下数据,可以得出D=1 mm和D=9 mm时,其数学模型如式(6)、式(7)所示:
f1=7.04sin(0.002149x+1.178)+
6.42sin(0.03449x-1.456)
(6)
f9=0.4159sin(9.946×10-5x+1.458)+
0.3897sin(0.03515x-1.6117)
(7)
为了验证推演数据的有效性,按照原实验的极限条件,将相应参数代入式(6)和式(7)中,获得推演数据如图4所示。图中结果显示,推演结果基本为正弦变化规律,与原实验结果相似。

图4 D=1 mm与9 mm的推演结果Fig.4 Deduction result of D=1 mm and D=9 mm
为更好的对比推演数据的有效性,将推演数据与原实验数据集成到同一图中进行对比分析,结果如图5所示。结果表明,根据该二次参数拟合推演方法得出的图像与已知曲线图像趋势是完全一致的,其平滑度有微小差异,但是这种差异在精度允许的范围之内。为了提高该方法的精度,可以适当的对b1、b2和c1、c2进行微小的调整,并再次进行拟合检验。
由此可以看出,该方法可以很好的由已知实验数据推演出极限条件下的数据,并用数据处理软件辅助模拟出相应的曲线图像,从而验证推演出的极限数据是否有效。

图5 推演数据与原实验数据对比结果Fig.5 Comparison result of the deduction data and the original experimental data
3 结论
本文提出了一种二次参数拟合推演方法,利用已有实验数据规律,推演出极限条件下数据模型,获取相应的极限数据与数据图像并与已有数据图像进行对比检验。推演实例结果表明,根据该二次参数拟合推演方法得出的数据精确有效,图像与已有图像趋势完全一致,并且存在的微小误差在精度允许范围内。该方法可有效解决工程实验中,在实验条件有限的情况下,求取极限条件下关键数据的问题。
[1] 文毅,李春波,白作霖,等.基于几何推理的坐标测量机测头选择及可达性分析[J].重型机械,1997(5):31-35.
[2] 宁连华.数学推理的本质和功能及其能力培养[J].数学教育学报,2003,8(03):42-45.
[3] 沈彦文.全站仪辊系平行度测量的数据处理方法[J].机械工程师,2009(08):39-40.
[4] 王立国,胡超,黄文虎.数学机械化在转子动力学研究中的应用初探[J].中国电机工程学报,2001,8(21):6-9.
[5] 林建冬,原思聪,郑建校.基于Pro/E与ANS YS的CAD/CAE数据交换方法研究[J] .工程机械,2007,8(38):32-36.
[6] 井平安,王仲民,邓三鹏,等.基于VB的PM 2.5采样器数据处理软件的研究[J].机械工程师,2015(09):42-43.
[7] 王高锋,王有飞,孙向阳.2K-V型减速机回转精度的仿真研究[J].重型机械,2009(06):34-39.
[8] 赵晓平,赵秀莉,侯荣涛,等.一种新的旋转机械升降速阶段振动信号的瞬时频率估计算法[J].机械工程学报,2011,47(07):104-108.
[9] 莫喜平.Ansys软件在模拟分析声学换能器中的应用[J].声学技术,2007,26(06):1280-1290.
[10]陈伟,马德军,宋仲康.弹性模量仪器化压入测试方法比较分析[J].机械工程师,2010(10):7-9.
[11]陈于平,伍星,刘畅.基于规则与案例的转子故障智能诊断方法[J].电子测量技术,2011,6(34):97-100.
[12]姚成玉,陈东宁,王斌.基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J].机械工程学报,2014,50(02):194-201.
Study on two parameter fitting and deduction method of limit test data of engineering experiment
SUN Feng, DONG Xiao-wei, XU Fang-chao
(Shenyang University of Technology, Department of Mechanical Engineering, Shenyang 110870, China)
In the engineering experiment, due to the limited experimental conditions, the critical experimental data under the limit condition cannot be obtained. To these problems, this paper proposes a method to measure the experimental data of limited conditions based on the measured experimental data. The method can reason out the data model under the limit condition according to the rules of the existing data, using the method of fitting with quadratic parametric, to obtain the deduction data of limit conditions. The result of the deduction shows that this method of limit condition data deduction is effective and feasible.
mathematical reasoning; function model; deduction method; quadratic parameter fitting
2016-04-22;
2016-06-02
孙凤(1978-),男,沈阳工业大学机械工程学院,副教授。
TP202.2
A
1001-196X(2016)06-0035-04
