基于ANSYS/LS-DYNA的钢筋剪切过程的数值模拟
2016-04-07徐贺伟卢秀春杨荣刚杨慧杰
徐贺伟,卢秀春,杨荣刚,王 键,杨慧杰
(燕山大学 机械工程学院,河北 秦皇岛 066004)
基于ANSYS/LS-DYNA的钢筋剪切过程的数值模拟
徐贺伟,卢秀春,杨荣刚,王 键,杨慧杰
(燕山大学 机械工程学院,河北 秦皇岛 066004)
剪切刀具是钢筋剪切机的核心部件,是剪切机研究的重要部分。分析钢筋剪切过程中的弹、塑性变形及断裂机理,简述钢筋剪切时剪切力的理论计算公式,以某厂钢筋随动剪切机剪切刀具为参考,建立钢筋剪切有限元模型,对剪切过程进行动力学仿真,分析参数对剪切力的影响,并用实验验证仿真结果的正确性,得出如下结果:增大上、下切刀侧向间隙,剪切力先减小后增大,侧向间隙为0.1 mm时,剪切力最小;增大上切刀刀刃倾角,剪切力减小。研究结果可为剪切机刀具设计与实验设备的安装调试提供理论依据。
钢筋剪切;有限元模型;剪切力
0 前言
钢筋切断机广泛应用于铁路、建筑、机械制造等行业,盘料供货的钢筋需要对其进行剪切获得所需长度。随着科技的进步,现有钢筋剪切机的性能已不能适应用户的需求,还需对其进行深入研究,使剪切机达到更好的使用性能[1]。
由于生产的需要,使得钢筋切断机得到迅速发展,许多学者对其进行了研究。文献[2]对钢筋剪切过程进行了动态仿真,分析了剪切过程中剪切力的变化规律,得到钢筋模型被剪断时的应力、应变动态分布规律;文献[3]对圆盘剪剪切力计算公式进行讨论,并得到剪切过程中铜板的应力应变状态及剪切力变化曲线;文献[4]推导了斜刃剪切的刀刃曲线方程,得出斜刃剪切时剪切力比平刃剪切时小的结论。
目前,学者们只对钢筋剪切时剪切力变化进行了动态检测,并未研究上下切刀间隙、切刀刀刃倾角等参数对剪切力变化规律的影响。本文的主要工作是建立钢筋剪切模型,用有限元软件对剪切过程进行模拟,对剪切过程中的应变及剪切力进行分析,研究上下切刀侧向安装间隙、上切刀刀刃倾角的变化对剪切力变化规律的影响,并用实验验证模拟结果的可靠性,为钢筋剪切机刀具的安装及刀具的设计提供参考。
1 剪切力理论公式计算
钢筋剪切过程分为四个阶段:第一阶段为钢筋的弹性变形阶段,开始剪切时上、下切刀对钢筋的挤压应力还没有达到钢筋的弹性极限,此时应力应变成正比,当切刀的挤压应力消失时,钢筋变形消失;第二阶段为钢筋的塑性变形阶段,随着剪切的进行,当刀具对钢筋的挤压应力大于钢筋的弹性极限时,钢筋发生不可恢复的塑性变形;第三阶段为钢筋的撕裂阶段,当上切刀继续施加对钢筋的纵向剪切时,钢筋的变形越来越大,钢筋的变形抗力越来越大,此时钢筋的受剪面积随着变形程度的加大而减小,所以钢筋单位面积所受到的剪切应力增大,当剪切应力达到剪切强度时,剪切面晶粒发生错位,在与刀片接触两端出现剪切裂纹;第四阶段为断裂阶段,动刀片继续剪切,第三阶段出现的裂纹扩大最后断裂,剪切结束[5-7]。
钢筋剪切过程是一个复杂的过程,目前为止,剪切力没有一个精确的计算公式。实验过程中取PC钢棒直径为10 mm,强度极限为460 MPa,钢筋进给速度为60 m/min。在工程实际应用中[8],剪切力大小采用如下公式计算
Pmax=K1K2Aσb
(1)
式中,K1为剪刃磨钝系数,一般取K1=1.2左右;K2为抗剪极限强度与抗拉极限强度之比,一般取K2=0.6左右;A为钢棒横截面面积,mm2; 为材料强度极限,MPa。
2 有限元模拟
2.1 剪切模型的建立
以某厂钢筋随动剪切机刀具为参考,建立剪切有限元模型,如图1所示。上切刀如图2所示,刃口设计成具有一定半径的圆弧,刀刃沿厚度方向有一定倾角。剪切过程中下切刀固定不动,上切刀在液压装置的带动下在垂直方向对钢筋进行剪切,剪切结束上切刀回到初始位置。
模拟过程中,钢筋材料选取为Q235,参数值见表1。上、下切刀定义为刚体,切刀材料密度7 860 kg/m3;弹性模量2.07×105MPa;泊松比0.3。上、下切刀和钢筋选取单元类型为SOLID164,切刀采用自由网格划分,钢筋采用映射网格划分,对钢筋剪切区域进行网格细化;仿真过程中,上、下切刀与钢筋接触类型定义为自动面面接触(ASTS),ASTS为双向接触。模拟过程中,双向接触即检查主面节点对从面的穿透,又检查从面节点对主面的穿透,从而定义了整个剪切过程中的各个接触;对下切刀所有自由度进行约束,上切刀约束所有旋转自由度和X、Z方向移动自由度,对钢筋轴线约束绕X轴旋转自由度;给上切刀沿Y轴负方向的初速度1.2 m/s,计算时间设置为0.01 s。

1.下切刀 2.上切刀 3.钢筋图1 剪切模型Fig.1 Model of cutting

图2 上切刀Fig.2 Upper cutter
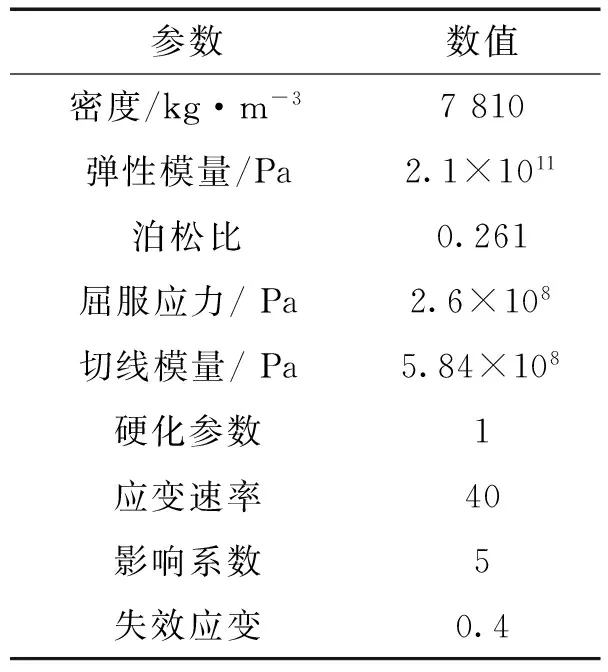
参数数值密度/kg·m-37810弹性模量/Pa2.1×1011泊松比0.261屈服应力/Pa2.6×108切线模量/Pa5.84×108硬化参数1应变速率40影响系数5失效应变0.4
2.2 有限元模拟结果
取直径为10 mm的钢筋对剪切过程进行模拟,模拟时上、下刀片间侧向间隙取0.1 mm,上刀片刀刃倾角取3°。
图3为剪切开始与剪切结束时刻钢筋塑性应变分布图,从图中可以看出,距离切口越近处塑性应变越大,沿着切口向外塑性应变逐渐减小。参数设置过程中设置的失效应变为0.4,而剪切结束应变图中塑性应变最大值为0.3999,比设定值偏小,产生此种现象的原因为有限元仿真中使用单元失效法,剪切过程中失效单元被删除。
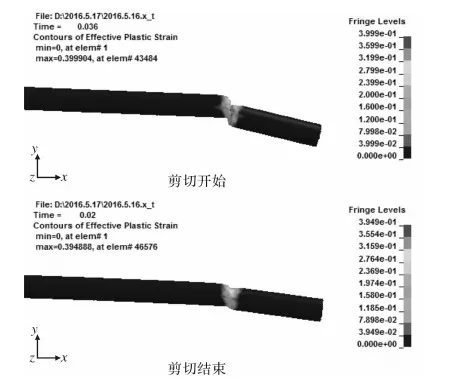
图3 剪切钢筋塑性应变图Fig.3 Diagram of plastic strain during cutting steel bar
图4为整个剪切过程中剪力变化曲线,此模拟过程与文献[9]及文献[10]所得剪切力变化规律一致。从上切刀接触到钢筋开始,随着上切刀切入深度的增加,剪切力逐渐增大,当上切刀剪切一定深度时(此深度与被剪切钢筋抗拉强度等参数有关),剪切力达到最大值,钢筋变形转为滑移阶段,剪切力逐渐变小。

图4 剪切力曲线Fig.4 Curve of cutting force
2.3 参数对剪切力的影响分析
侧向间隙是指上、下刀片沿钢筋轴线方向的安装距离,侧向间隙过小,可能导致剪切时上刀片与下刀片产生摩擦,刀片磨损加快,影响剪切进行;侧向间隙过大,将引起剪切时钢筋的震动,影响剪切断面质量,使断面毛刺增多,对剪切精度产生一定影响。
上、下切刀侧向间隙的变化对剪切力的影响如图5所示,剪切力随刀具侧向间隙的增加先减小后增大;侧向间隙为0.1 mm时,钢筋剪切力最小,此时剪切力为19.55 kN;侧向间隙在0.2~0.3 mm之间时,剪切力增大速率较快。

图5 上下切刀轴向间隙对剪切力影响Fig.5 Effect of axial gap between upper and lower cutter on cutting force
上切刀刀刃沿厚度方向倾角的大小对剪切力有一定影响,倾角过小不利于钢筋剪切,不能保证钢筋剪切面的质量;倾角过大使刀具磨损加快,频繁更换刀具影响生产效率。
上切刀刀刃倾角对剪切力的影响如图6所示,实验时取上、下切刀侧向安装间隙为0.1 mm。由图可见,剪切力随着上切刀刀刃倾角的增大逐渐减小,刀刃倾角小于3°时,剪切力变化较快;刃倾角大于3°小于4°时,剪切力基本不变。

图6 上切刀刀刃倾角对剪切力影响Fig.6 Effect of upper cutter edge angle on cutting force
3 模拟与实验对比分析
采用实验方法对仿真结果可靠性进行验证,实验使用的仪器为燕山大学轧制中心为某企业生产的钢筋随动剪切机,在上切刀上粘贴电阻式应变片对剪切力进行测量,电阻应变片将应变转化为电阻的变化,利用电桥将电阻变化转变为电压变化,将信号送入放大器,利用标定曲线推算出剪切力大小。实验时取上切刀刀刃倾角为3°,实验所用钢筋随动剪切机与剪切钢筋如图7所示。

图7 随动剪切机及剪切钢筋Fig.7 Cutting machine and steel bar
表2为上、下切刀在不同侧向间隙下钢筋剪切力实验与仿真结果对比,实验数据的获得是在同一参数下进行五次实验,将剪切力取五次实验平均值。由表中数据得出,实验结果均大于仿真结果,出现这种现象的原因是仿真时没有考虑钢筋形变及外界条件等因素的影响。实验所得剪切力随上、下切刀侧向间隙变化规律也是先增大后减小,与有限元模拟结果相同;实验剪切力与仿真所得剪切力误差在7%以内,此值在合理范围内,实验验证了仿真结果的可靠性。
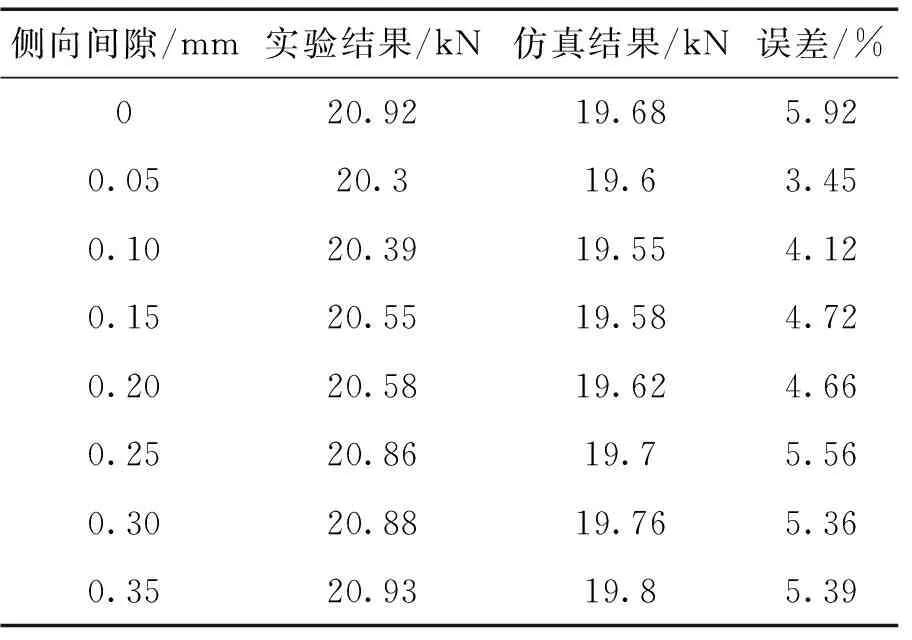
表2 剪切力实验与仿真结果
4 结论
以某企业钢筋随动剪切机的刀具为建模依据,建立钢筋剪切模型,对剪切力进行理论公式计算,用有限元软件对钢筋剪切过程进行模拟,研究参数对剪切力的影响规律,并用实验验证仿真结果的正确性。结果表明:钢筋剪切力是一个先增大后减小的渐变过程。上、下切刀侧向间隙增大,剪切力先减小后增大,侧向间隙为0.1 mm时剪切力最小;剪切力随上切刀刀刃倾角的增大而减小;实验所得剪切力随上、下切刀侧向间隙的变化规律与仿真结果一致,且实验误差与仿真误差在合理范围内,验证了仿真结果的可靠性。研究结果为钢筋剪切机刀具的安装及刀具的结构优化提供理论基础。
[1] 孟进礼, 卫青珍. 对钢筋切断机发展的几点看法[J]. 建筑机械化, 2000,21(5): 14-15.
[2] 刘中, 朱振华, 卫青珍. 基于LS-DYNA 的钢筋切断机剪切钢筋的动态仿真[J]. 太原科技大学学报, 2011,32(1):33-36.
[3] 戴志凯, 许 平, 张宝勇, 等. 基于LS-DYNA的分条圆盘剪切力的计算研究[J]. 新技术新工艺, 2013:69-71.
[4] 孟 凡, 李郝林.基于ANSYS/LS-DYNA的碎边剪切力计算研究[J]. 机械工程与自动化, 2015(2):45-47.
[5] 王伯平. 钢筋切断机切断钢筋的机理分析[J]. 建筑机械化,1988,9(7): 20-22.
[6] 章友文. 钢筋切断机剪切机理分析[J]. 工程机械,1991, 22(3): 16-19.
[7] 刘鸿鹰. 钢筋剪切塑变理论分析[J]. 建筑机械化,1996, (2): 8-10.
[8] 杨中锋. 凸轮摆杆剪切系统研究及性能分析[D]. 秦皇岛: 燕山大学,2013.
[9] 段红杰, 陶 浩. 钢筋切断机动力学仿真设计[J]. 制造业自动化, 2010, 32(4): 143-145.
[10]陶 浩, 段红杰. 钢筋切断机的动力学性能[J]. 煤矿机械, 2008, 28(5): 81-83.
Numerical simulation of steel bar shearing process based on ANSYS/LS-DYNA
XU He-wei, LU Xiu-chun, YANG Rong-gang, WANG Jian, YANG Hui-jie
(College of Mechanical Engineer, Yanshan University, Qinhuangdao 066004, China)
Cutter is an important part of steel bar cutting machine. The elastic-plastic deformation and fracture mechanism of steel bar are analyzed during cutting. Cutting formula is listed. Cutting model is found based on a factory’s steel bar cutting machine. Dynamics simulation of cutting process is done, and parameters influence on cutting force are analyzed, and the reliability of simulation results is verified by experiments. A series of simulation results are obtained. Cutting force is decreasing first and then increasing with the increase of side gap between upper and lower cutter, and cutting force is the smallest when the distance is 0.1mm. Cutting force is decreasing with the cutting edge angle increase of upper cutter. The results provides theoretical basis for the cutting machine design and installation.
steel bar shearing; finite element model; cutting force
2016-05-25;
2016-07-12
徐贺伟(1990-),女,燕山大学机械工程学院,硕士研究生。
卢秀春(1954-),男,燕山大学机械工程学院教授,研究方向:机械设计及理论。
TG333.2+1
A
1001-196X(2016)06-0021-04
