基于加权改进MUSIC算法的相干信号波达方向估计
2016-04-07张剑云朱家兵张正言
黄 超,张剑云,朱家兵,张正言
(1.解放军电子工程学院,安徽 合肥 230037;2.中国电子科技集团公司第三十八研究所,安徽 合肥 230088)

黄超1,张剑云1,朱家兵2,张正言1
(1.解放军电子工程学院,安徽 合肥 230037;2.中国电子科技集团公司第三十八研究所,安徽 合肥 230088)
摘要:针对传统波达方向估计算法对相干信号失效的问题,提出了基于加权-改进多信号分类法(MUSIC)的波达方向估计算法。该算法首先对接收数据协方差矩阵进行重构,进而构造出新的噪声子空间,再根据特征值大小对噪声子空间特征向量进行加权,完成对相干信号的波达方向估计。仿真分析表明,算法成功地完成了对相干信号的波达方向估计。
关键词:相干信号;矩阵重构;加权-改进;波达方向估计
0引言
波达方向(Direction of Arrivals,DOA)估计是阵列信号处理中的一项关键技术,常被应用于雷达、通信、声呐和地震勘探等领域[1]。在DOA估计算法中,多信号分类算法是最经典的算法之一,它一般通过谱峰搜索来检测信号的DOA。该算法对不相干或相干程度较小的信号具有较高的的空间分辨率,但随着信号相干程度的增加,空间分辨率就会逐渐下降,直至完全失效[2-3]。
而在信号多径传播或存在欺骗干扰的情况下,信号之间常常是完全相干的,MUSIC算法完全失效。为了完成相干信号的DOA估计,就必须对相干信号进行解相干处理。解相干算法主要分为两类:一是降维处理,二是非降维处理。降维处理解相干主要包含空间平滑类算法[4-5]。其中,双向空间平滑(Forward and Backward Spatial Smoothing,FBSS)算法综合性能较好,但它在解相干的过程中牺牲了阵列孔径,而且计算较为复杂。非降维处理主要通过将数据接收矩阵构造成Toeplitz矩阵[6-7]来实现解相干。
针对MUSIC算法对相干信号失效的问题,文献[8-9]提出了改进的MUSIC(Modified Multiple Signal Classifi-cation,MMUSIC)算法,MMUSIC算法通过对接收信号协方差矩阵作预处理,使重构后的协方差矩阵满足Toeplitz特性,并且协方差矩阵分解后得到的信号子空间与噪声子空间能够正交,从而降低了噪声的影响。但当信噪比很低、信号入射角度间隔很小且相关时,MMUSIC算法就不能准确地区分信号,DOA估计性能降低。针对这个问题,本文对该算法做进一步改进,提出了加权-改进MUSIC(Weighted-modified Multiple Signal Classifi-cation,WMMUSIC)算法。
1MUSIC算法及其改进算法
1.1信号模型
假设有N个窄带远场信号入射到M元均匀直线阵列,入射角度为θi(i=1,2…,N),信号波长为λ,阵元间距d=λ/2,则阵列接收信号矢量为:
X(t)=As(t)+n(t)
(1)
其中,X(t)=[x1(t),x2(t),…,xM(t)]T是阵列输出矢量,A是阵列流型矢量,s(t)是入射信号矢量,n(t)是阵列噪声矢量,假设n(t)是均值为0、方差为σ2的高斯白噪声。
s(t)=[s1(t),s2(t),…,sN(t)]T
(2)
n(t)=[n1(t),n2(t),…,nM(t)]T
(3)
A=[a(θ1),a(θ2),…a(θN)]
(4)
a(θi)=[1,exp(φ),…exp((M-1)φ)]T
(5)

1.2MUSIC算法
MUSIC算法是最经典的超分辨DOA估计算法之一,它首先构造接收数据的自相关阵,然后对该自相关阵做特征分解并构造相应的特征子空间,最后通过特征子空间确定信号的到达方向。接收数据X(t)=As(t)+n(t),则它的协方差矩阵
RX=E[X(t)X(t)H]=ARsAH+σ2I
(6)
假设待估计信号之间相互独立,Rs=E[s(t)s(t)H]为满秩矩阵,RX的秩为待估计信号的个数N,对RX进行特征分解:
(7)

信号子空间也可以由A张成,即span[Es]=span[A]。由于span[En]⊥span[Es],可知span[En]⊥span[A],可推出AHEn=0,即A的N个导向矢量与噪声子空间的特征向量正交。利用该正交关系可构造MUSIC空间谱估计为:
(8)
MUSIC算法在理想条件下具有良好的性能,但在信号相干时算法的性能会受到严重影响。当信号源完全相干时,阵列接收的数据协方差秩为1,这将会导致信号子空间的维数小于信号源数,导致相干源的导向矢量与噪声子空间不完全正交,从而无法正确估计信号源方向。所以解相干的核心问题是如何通过一系列处理或变换使得信号协方差矩阵的秩得到有效恢复,从而正确估计信号源的方向。
1.3MMUSIC算法
空间平滑类算法能够解决相干信号源的问题,但是,由于将接收阵列分成了多个子阵,减小了阵列孔径,使得阵列的分辨率降低;同时也减小了可估计信源的数目,增加了算法的运算复杂度。对此,一些学者提出了MMUSIC算法,其实质是FBSS算法中的一种特殊清况,能够对相干信号进行DOA估计。该方法以阵列自身为子阵,使得平滑后阵列的孔径保持不变,保证了阵列的分辨率;同时由于该方法只有一个子阵,运算量相对于双向空间平滑算法有一定的降低。MMUSIC算法的基本原理如下:
阵列接收数据为X(t)=As(t)+n(t),令
Y(t)=JX*(t)
(9)
其中,X*(t)是X(t)的复共扼,J是M×M阶交换矩阵,JHJ=1。
(10)
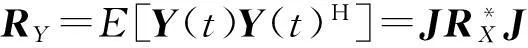
(11)
用R替代RX进行特征值分解,获得新的特征值和特征向量,并依此构造出新的噪声子空间Vn。则MMUSIC算法的空间谱估计函数为:
(12)

2.1算法原理及流程
在MMUSIC算法中,通过对接收数据X(t)进行数学变换得到Y(t),然后分别求出X(t)和Y(t)的自协方差矩阵,最后用求出的两个自协方差矩阵的均值来代替原先接收数据X(t)的协方差矩阵进行特征值分解。在该方法中,仅仅利用了X(t)和Y(t)的自协方差矩阵信息,而并没有考虑X(t)和Y(t)的互协方差矩阵信息。本文基于MMUSIC算法,充分利用X(t)和Y(t)的自协方差矩阵和互协方差矩阵信息,构造新的增广矩阵;然后对新的接收数据矩阵进行奇异值分解得到相应的噪声子空间,并与传统的MUSIC算法分解得到的噪声子空间按特征值大小进行比较,选择较大特征值对应的特征向量来构造新的噪声子空间;并针对噪声子空间中特征向量不完全一致的情况,根据特征值大小对特征向量进行加权,提出一种加权-改进MUSIC (WMMUSIC)算法。WMMUSIC算法的基本步骤如下:
1)构造增广接收数据矩阵
令Y(t)=JX*(t),则
(13)
充分利用互协方差信息,构造增广矩阵,令Rnew=[RXRYRXYRYX]。
2)构造新的噪声子空间和加权值
对Rnew进行奇异值分解
[U,S,V]=svd(Rnew)
(14)
其中,特征值矩阵S=diag(λs1,λs2,…λsM),特征值按从大到小排列,特征向量矩阵U=[u1,u2,…uM]。由式(7)知RX=EΛEH,将S和Λ中的特征值作比较,选择对应位置较大的特征值构造新的特征值矩阵Snew=diag(λnew1,λnew2,…,λnewM),同时选择新特征值对应的特征向量构造新的特征向量矩阵Unew,则可得到新的噪声子空间为:
UNnew=Unew(N+1:M)
(15)
针对新的噪声子空间构造加权值W。
(16)
3)谱峰搜索
基于WMMUSIC算法的空间谱估计函数为:
(17)
2.2算法的运算量分析
FBSS算法的运算量:1)若选取子阵长度为m,则数据协方差矩阵估计的运算量为2×O(L(M-m+1)m2),L为快拍数;2)对协方差矩阵进行奇异值分解,其运算量为O(m3);则总的运算量为2×O(L(M-m+1)m2)+O(m3)。
WMMUSIC算法的计算过程与MMUSIC算法相当,协方差矩阵估计时构造了增广矩阵Rnew=[RXRYRXYRYX],估计RX、RY的运算量为O(L(M2+2M)),RXY与RYX互为共轭转置,估计RXY与RYX的运算量为O(LM2),则算法总运算量为O(2LM2+2LM+M3)。
3仿真分析
为了分析WMMUSIC算法的DOA估计性能,采用阵元数为8的均匀直线阵进行仿真实验。阵元间距取为d=λ/2,入射信号为窄带远场信号,噪声为均值为0,方差为1的复加性白噪声。
实验1验证WMMUSIC算法DOA估计的有效性
假设两个窄带远场全相干信号,它们的入射角度分别为-10°和0°,信噪比为SNR=10 dB,快拍数为512,DOA估计结果如图1所示。两个窄带远场不相干信号,它们的入射角度分别为-10°和0°,其余条件相同,DOA估计结果如图2所示。三个窄带远场信号,其中前两个信号全相干,第三个信号是非相干信号,入射方向分别为-30°、0°和25°,其余条件相同,DOA估计结果如图3所示。
图1至图3证明了本文WMMUSIC算法对相干信号、独立信号以及两者的混合信号均能进行DOA估计。
实验2 WMMUSIC算法对相干信号的DOA估计性能分析
假设两组全相干信号,一组的入射角度分别为-10°和0°,信噪比为SNR=10 dB,快拍数为512;另一组的入射角度为5°和0°,信噪比为SNR=5 dB。两组实验中加WMMUSIC算法、MMUSIC算法的DOA估计仿真结果如图4、图5所示。
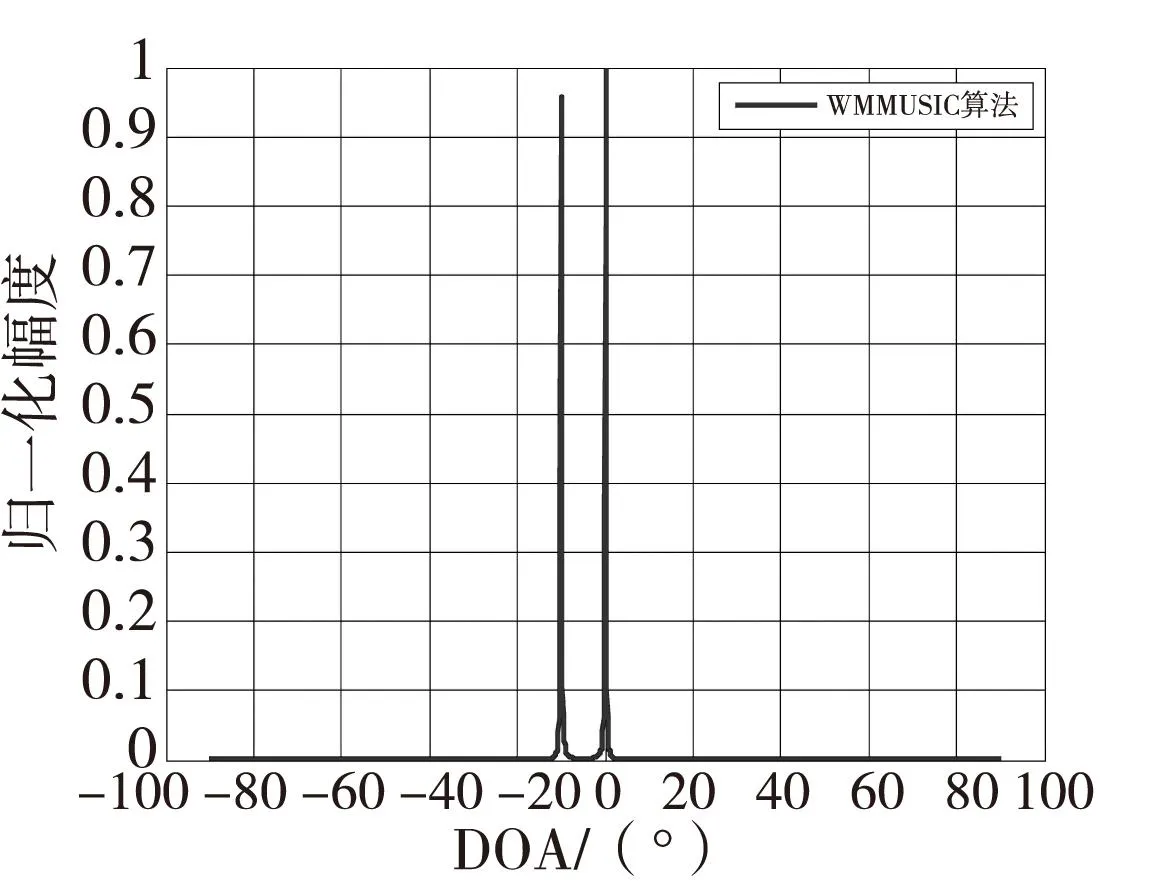
图1 相干信号DOA估计Fig.1 Coherent signals DOA estimation

图2 独立信号DOA估计Fig.2 Incoherent signals DOA estimation

图3 混合信号DOA估计Fig.3 Mixed signals DOA estimation
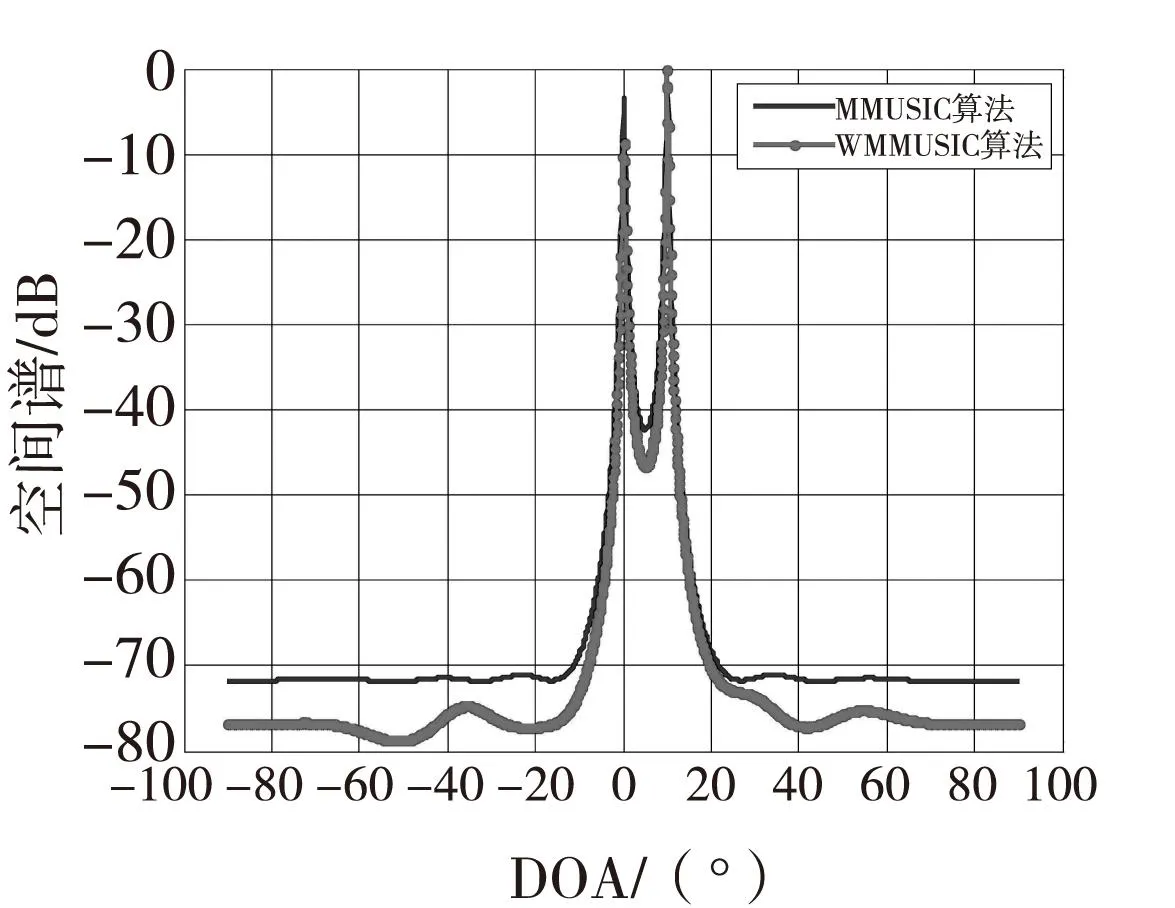
图4 DOA估计比较(SNR=10 dB,角度间隔为10°)Fig.4 The comparison of DOA estimation

图5 DOA估计比较(SNR=5 dB,角度间隔为5°)Fig.5 The comparison of DOA estimation
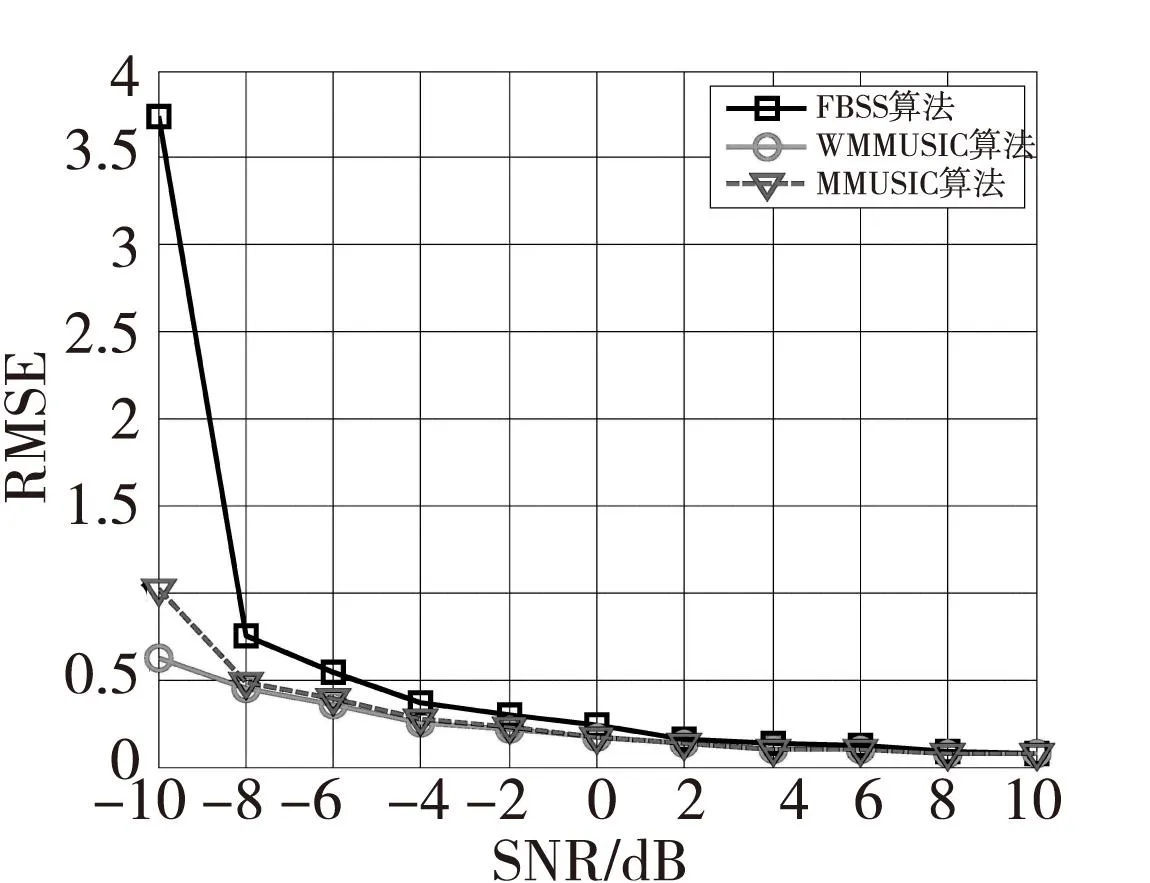
图6 RMSE与信噪比之间的关系Fig.6 The relationshipbetween RMSE with SNR
由图4、图5可看出,当信噪比为SNR=10dB,信号角度间隔为10°时,本文的WMMUSIC算法和MMUSIC算法均具有良好的DOA估计效果,但本文算法谱峰更加尖锐,分辨率更高。当信噪比和信号角度间隔分别降低至5dB和5°时,MMUSIC算法已经不能进行有效分辨,但本文算法依然可以准确地区分出两个相干信号。
由图6可看出,在快拍数一定的情况下,随着信噪比的增大,三种DOA估计算法的RMSE逐渐减小,估计精度增高。在信噪比较低时,WMMUSIC算法的RMSE比MMUSIC算法略低,远好于FBSS算法。这说明本文的WMMUSIC算法在低信噪比时拥有更高的DOA估计精度。
由图7可看出,在取低信噪比SNR=-10dB的情况下,随着快拍数的增大,三种DOA估计算法的RMSE逐渐减小,估计精度增高。当快拍数较小时,WMMUSIC算法的RMSE低于MMUSIC算法和FBSS算法。说明在快拍数较小时,本文的WMMUSIC算法DOA估计精度优于其他两种方法。
实验3WMMUSIC算法的运算量分析
假设阵元数M=8,快拍数在1到512之间变化,算法运算量的变化如图8所示。假设快拍数为L=512,阵元数在8到20之间改变,仿真结果如图9所示。设定双向空间平滑算法的子阵长度为M-3。
对比图8、图9可知,阵元数对运算量的影响要大于快拍数对运算量的影响,这是因为快拍数只能决定协方差矩阵估计的运算量。当阵元数逐渐增大时,算法运算量显著增加,本文WMMUSIC算法的运算量略高于MMUSIC算法,但远小于FBSS算法的运算量。

图7 RMSE与快拍数之间的关系Fig.7 The relationship between RMSE with snapshots

图8 运算量与快拍数的关系Fig.8 The relationship between computation withsnapshots

图9 运算量与阵元数的关系Fig.9 The relationship between computation with array elements
4结论
本文提出了基于加权-改进MUSIC算法的相干信号DOA估计算法。该算法在MMUSIC算法的基础上,充分利用互协方差信息,通过构造增广矩阵得到新的协方差矩阵;然后对新的接收数据矩阵进行奇异值分解得到相应的噪声子空间,并与传统的MUSIC算法分解得到的噪声子空间按特征值大小进行比较,选择较大特征值对应的特征向量来构造新的噪声子空间;最后根据特征值大小对噪声子空间特征向量进行加权,完成对信号的DOA估计。仿真分析表明,该算法没有孔径损失,能够在低信噪比情况下分辨出间隔较小的相干信号;在低信噪比和低快拍数的情况下,DOA估计精度优于FBSS算法和MMUSIC算法;算法运算量远低于FBSS算法,但略高于MMUSIC算法。下一步将在降低算法的运算量、提升算法在信号角度间隔较小时的DOA估计性能方面展开进一步研究。
参考文献:
[1]PuskaH,SaarnIsaarihInattij.Serialsearchcodeacquisitionusinganartantennaswithsinglecorrelatorormatchedfilter[J].IEEETransationsonCommunication(S0090-6778), 2008,56(2):299-307.
[2]RoyR,KailathT.ESPRIT-estimationofsignalparametersviarotationalinvariancetechniques[J].IEEETrans.onAcaustics,SpeechandSignalProcessing, 1989, 37(7):984-995.
[3]KavehM,BarabellAJ.ThestatisticalperformanceoftheMUSICandtheminimum-normalgorithmsinresolvingplanewaves[J].IEEETrans,onAcoustics,SpeechandSignalProcessing, 1986,34(2):331-341.
[4]吴海普,张莉,吴瑛.相干信号源空间平滑法及其改进[J].信息工程大学学报,2001,2(4):31-34.
[5]董玫,张守宏,吴向东.一种改进的空间平滑算法[J].电子与信息学报,2008,30(4):859-862.
[6]HANFangming,ZHANGXianda.AnESPRIT-likealgorithmforcoherentDOAestimation[J].IEEEAntennasandWirelessPropagationLetters, 2005(4):443-446.
[7]LIULiguo,CAIYibing,WANGHaisong,etal.AnimprovedESPRIT-likealgorithmforcoherentsignalanditsapplicationfor2-DDOAestimation[C]//7thInternationalSymposiumonAntennas,Propagation&EMTheory.Singapore:IEEE,2006: 1-4.
[8]赵谦,董民,梁文娟.DOA估计算法的一种修正MUSIC算法的研究[J]. 计算机工程与应用,2012, 48(10):102-105.
[9]洪伟. 一种对修正MUSIC算法的改进测向方法[J]. 船舶电子对抗, 2011, 34(3) :71-73.
DOA Estimation of Coherent Signals Based on Weighted-modified MUSIC Algorithm
HUANG Chao1, ZHANG Jianyun1, ZHU Jiabing2, ZHANG zhengyan1
(1.Electronic Engineering Institute, Hefei 230037, China;2.No.38 Research Institute of CETC, Hefei 230088, China)
Abstract:Because classical DOA(Direction of Arrival) estimation algorithms often fail to deal with coherent signals, a new DOA estimation algorithm based on weighted-modified MUSIC(Multiple Signal Classifi-cation) algorithm was proposed in this paper. In this algorithm, the data covariance matrix was reconstructed at first, and new noise subspace was constructed then. Finally the eigenvectors of noise subspace were weighted based on the size of the gain value, and the DOA estimation of coherent signals was completed. Computer simulation indicated the algorithm estimated the DOA of coherent signals successfully.
Key words:coherent signals; matrix reconstruction;weighted-modified;DOA estimation
中图分类号:TN957.51
文献标志码:A
文章编号:1008-1194(2016)01-0042-05
作者简介:黄超(1991—),男,安徽舒城人,硕士研究生,研究方向:雷达信号处理、阵列信号处理。E-mail:18226658179@163.com
基金项目:中国博士后科学基金(2014M552606);安徽省自然科学基金项目资助(1408085MF111)
*收稿日期:2015-08-05
