基于部分可见星的接收机完好性监测方法

吴　杰，彭　敖，石江宏

(厦门大学 通信工程系，福建　厦门　361005)



基于部分可见星的接收机完好性监测方法

吴杰，彭敖，石江宏

(厦门大学 通信工程系，福建厦门361005)

摘要：传统的伪距残差检测接收机自主完好性监测算法在无法获得较为准确的接收机先验位置信息时，先验位置偏差往往会对各颗卫星的伪距残差造成严重影响，从而导致故障检测与识别出错。因此可能将含有粗差的观测值用来定位，而剔除了高质量的观测值。特别是在多颗卫星观测值受粗差影响的情况下，定位精度将严重恶化。为了解决此问题，本文提出了一种基于部分可见星定位结果的鲁棒接收机自主完好性监测算法，算法首先利用了部分可见卫星观测值进行最小二乘的粗略定位，并用此定位结果来计算伪距残差量。同时为了保证此粗略定位结果的精度满足后续伪距残差检测的要求，本文还提出了一种鲁棒性的基于最小平方中值的方法对其进行精度估计。此外，本文也从理论上推导与分析了所提出的接收机自主完好性监测算法的门限值。最后利用仿真与实测数据对所提出的方法与传统最小二乘伪距残差检测法进行了性能对比测试实验，结果表明：本文所提出的方法在复杂环境下对故障卫星的漏排除率比最小二乘伪距残差检测方法有明显的降低(实验中降低了7.77%)，定位结果的精度也比传统最小二乘伪距残差检测方法有明显的改善。

关键词：接收机自主完好性监测；接收机先验位置；伪距残差；故障检测与识别；鲁棒；最小平方中值；部分可见卫星

0引言

接收机自主完好性监测(receiver autonomous integrity monitoring，RAIM)，是指利用接收机冗余观测量进行一致性检测，来实现对卫星观测量的故障检测、识别和排除的技术。(当可见卫星达到5颗及以上时才能进行故障检测，6颗及以上才能进行故障识别与排除。)对完好性监测的研究，国外已经较为深入，而国内则关注较少。

目前常用的RAIM算法是只利用当前观测量的快照(Snapshot)算法，该算法只依靠当前时刻的冗余观测量就可完成故障检测与识别，典型的算法包括：文献[1]提出的伪距比较法，文献[2]提出的最小二乘残差法和文献[3]提出的奇偶矢量法。文献[4]指出，这三种方法具有等效性。都是首先利用接收机的先验位置计算出伪距残差量，而后基于若某颗卫星观测量存在粗差时，其伪距残差就会偏大的基本原理进行故障检测与识别。

由于快照算法具有不需要外部支持设备、反应速度快和容易实现等优点，得到了广泛的使用。然而，在含多粗差或大粗差环境下传统方法的监测效果并不理想。随着各国导航系统的建成，可见星数目急剧增加，多模接收情况下出现多粗差的概率将会增大，因此传统RAIM方法将难以满足导航系统的发展需求。

本文以传统最小二乘伪距残差法为例进行分析，抽象出传统方法在含多粗差或者大粗差环境下监测效果不理想这一问题的本质——无法获得较精确的接收机先验位置信息。然后针对这一问题，本文提出了一种基于部分良好观测量定位结果的伪距残差RAIM方法。最后，通过仿真和实测结果表明，本文所提出的方法能显著降低在多粗差以及大粗差场景下故障卫星的漏检测率与排除率，增强了在复杂环境下接收机完好性监测的可用性，提升了接收机的定位精度。

1传统最小二乘伪距残余算法描述

对于传统的最小二乘伪距残差检测算法[2]：

其伪距观测模型表示为

Z=HX+V

(1)

式(1)中，观测量Z等于接收机对相应卫星的距离测量值(ρ)与几何距离(R)以及钟差δt0之间的差值。

Z=ρ-R-δt0

(2)

式(2)中

(3)

XSi=(xsi,ysi,zsi)表示第i颗卫星的空间位置。Xp=(x,y,z)T表示接收机位置。

观测矩阵

X=(dx,dy,dz,δt)为接收机位置与钟差向量真实解与迭代初值之间的偏差。V∈Rn×1为观测噪声矢量，V～N(0，σ2)， 存在故障时V用V+δ代替[2]。

1.1故障检测

依据最小二乘原理，可计算出接收机状态的最小二乘估计解为

(4)

伪距残差为

(5)

式(5)中

SW=[I-H(HTH)-1HT]

(6)

构造统计检测量

(7)

将统计检测量γ与检测门限TD比较，若γ>TD， 则系统有故障；反之，系统无故障。其中检测门限TD依据误警率的要求进行设置。

1.2故障排除

检测出故障后，构造统计检测量[6]：

(8)

式(8)中，Zw(i)表示伪距残差向量的第i个元素；Sw(i,i)表示Sw对角线上第i个元素。

对统计量d(i)作二元假设：

无故障假设H0：E(d)=0， 则d～N(0,1)

有故障假设H1：E(d)≠0， 则d～N(δi,1)

利用最大似然法进行故障排除，每次排除d(i)最大值所对应的观测量，反复执行故障检测与故障排除，直至统计检测量γ小于检测门限值[7]。

具体流程见图1。

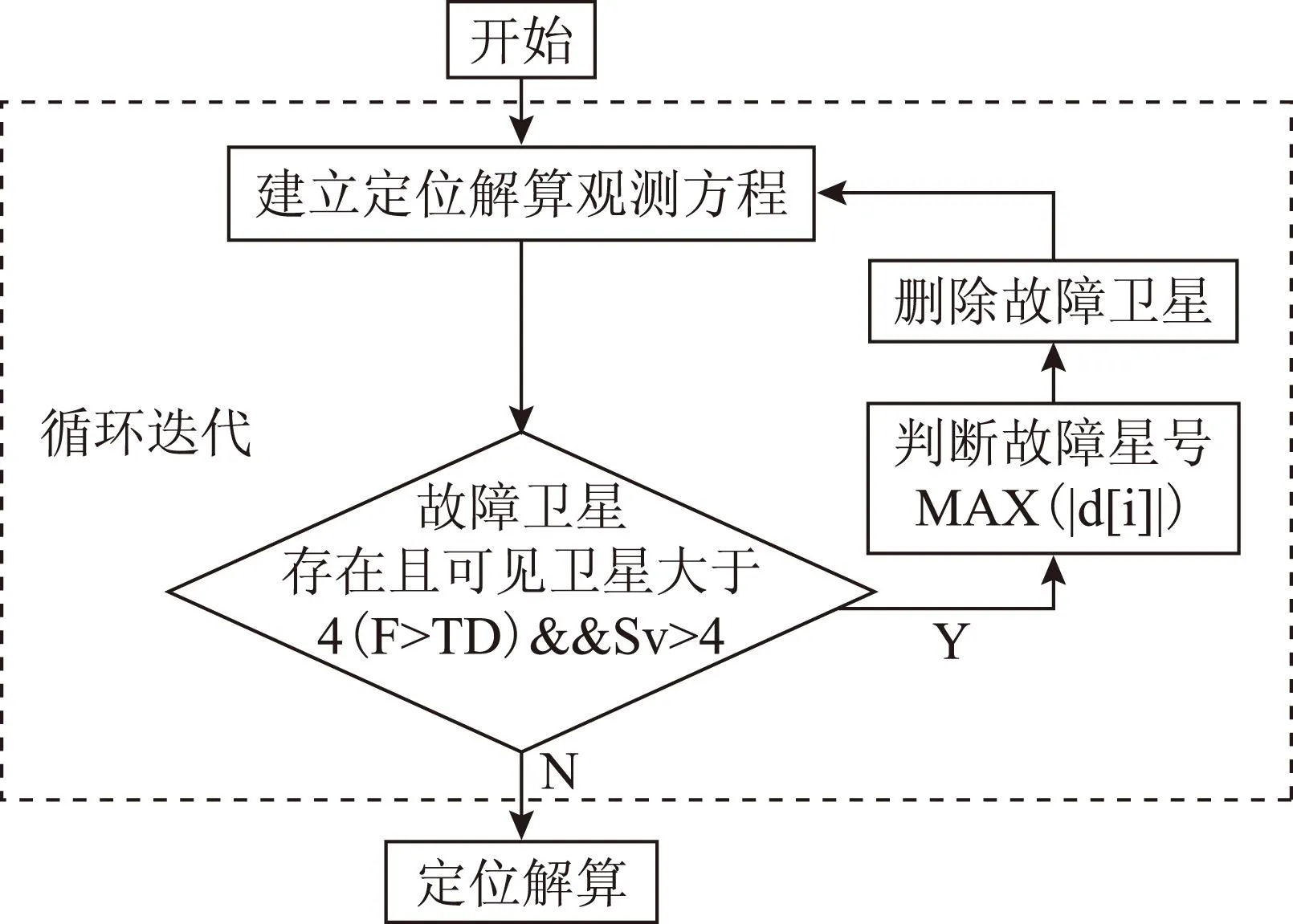
图1　传统方法的流程图

2问题描述与数学模型

2.1问题描述

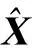
(9)

式(9)中，Rp为接收机先验位置与卫星间的几何距离。

然而，接收机先验位置的偏差，会使得所有可见星的伪距残差量都受到污染(即，某观测量的一个错误被所有观测量的残差吸收，如图2所示)，若采用传统方法进行故障排除，良好观测量被错误地舍弃是可能的，尤其是在大的或者多个粗差观测值存在时[8]。

本文对一个含有多个大粗差观测值的场景进行了连续840s的最小二乘残差RAIM方法检测，发现良好观测值的错误舍弃率高达17.5%。而含粗差的故障观测值的漏排除率为7.89%。

表1为一次错误故障识别与排除的实测数据(同一历元的数据，其中卫星编号1～32为全球定位系统(globalpositioningsystem，GPS)的导航卫星，33～46为我国北斗卫星导航系统(BeiDounavigationsatellitesystem，BDS)的导航卫星，本次测试数据来自位于厦门软件园典型城市峡谷环境，数据主要误差包括短多径误差、基带芯片跟踪环路不理想带来的粗差。)：本次观测场景共有15颗可见星，其中37、38、39、40、41号卫星观测值存在粗差。从表1记录的结果可以看出传统方法在这种存在多粗差观测值的场景下故障排除出现错误，错将良好观测量(5、15、30、29、10、6、34)排除而保留下了含粗差的观测量(38、41)。

表1　故障排除出错的一组数据

2.2数学模型

针对上述问题，从理论上分析，当定位场景出现含大粗差的观测值时，按照传统方法，此观测值至少会在首次循环迭代中用以计算接收机先验位置，从而直接破坏了先验位置Xpε的准确度。因此，导致了接收机与所有卫星的几何距离Rεi受到粗差污染(如图2所示)。进而污染到所有卫星的伪距残差量Zwε。

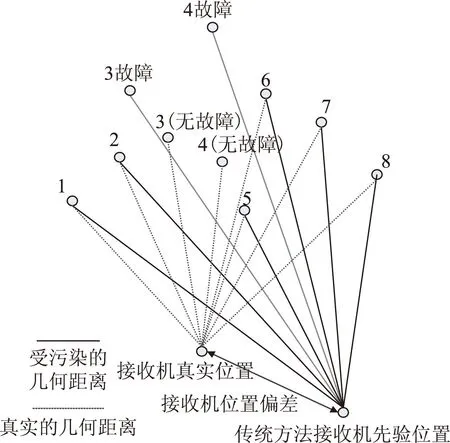
图2　先验位置对几何距离的影响

本文将含误差项εT的接收机位置表示为

(10)

由几何距离计算公式可得

Rεi=

(11)

因此，伪距残差量为

Zwε=ρ-Rε-δtε+Vp=ρ-δ+Vp-

(12)

任取一颗可见星观测量代入公式(12)进行伪距残差计算，并利用泰勒公式展开，可得其二次项系数

(13)

(14)

(15)

将式(15)代入式(14)可得

zi·(ρ-δtε-zi+vpi)≈(xsi-x-εx)εx+

(ysi-y-εy)εy+(zsi-z-εz)εz

(16)

对上式(16)两边求εx的偏导可得

(17)

将式(15)代入式(17)可得

(18)

将式(18)代入式(14)得zi·zi≈εx·εx+εy·εy+εz·εz， 即

(19)

式(19)中，vi为观测噪声量。

写成矩阵形式即

(20)

图3　定位误差—伪距残差实测数据

3基于部分可见卫星定位结果的RAIM方法

3.1算法提出

基于上述问题的分析可知，对于传统最小二乘伪距残差法，其问题本质在于采用了含较大误差的接收机先验位置信息来计算卫星的伪距残差。以至于残差引入了大的偏差，导致故障识别与排除错误。

针对以上问题，本文提出一种基于部分可见星(不含粗差观测值)定位结果的RAIM算法，本方法首先不断随机选取部分可见星的组合进行小范围粗略定位，并依据数学模型式(20)对此定位结果的精度进行评估(利用鲁棒性的最小平方中值法[9])，直到其精度值达到后续伪距残差的计算要求，再利用此结果来进行后续的伪距残差计算，最后，将残差量构造成服从高斯分布的统计判决量，进行故障检测、识别与排除。

算法核心在于：较之传统方法，本方法采用了有一定精度保障的接收机位置进行伪距残差计算，因此一定程度上保证了在故障检测与识别时，各卫星伪距残差量的准确度，从而避免了传统方法所出现的问题。

图4为本方法的示意图。

图4　所提出的RAIM方法示意图

3.2算法描述3.2.1基于部分可见星定位结果的精度评估

由上述数学模型可知，伪距残差量的大小直接反映了接收机位置的准确度。因此，本文通过判断各卫星伪距残差量的大小来估计接收机位置的准确度，具体方法采用鲁棒性的最小平方中值法(least median square，LMedS)[9]。

下面本文将讲述定位结果精度评估的具体流程。

首先，对所有可见星生成元素个数为4或者5的可见星组合，随机选取其中一个组合进行最小二乘定位解算。

(21)

并计算出此次小范围定位的PDOP值。

(22)

由观测模型式(10)，可得伪距残差量。

(23)

(24)

并选取伪距残差量均方根值的中位数构造检测量

(25)

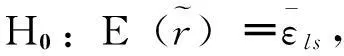
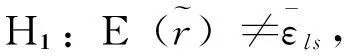
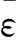
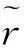
(26)

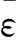
文献[10]对最小二乘解的精度进行了研究，指出，在消除大气层影响的情况下，最小二乘法水平定位精度均值在20m左右，高程定位精度均值在40m左右[10]，因此，整体的定位精度εls均值在45m左右。

在实测场景下，电离层延迟、对流层延迟是良好观测值伪距测量误差的最主要误差源，文献[11]指出，电离层延迟的误差在50～150m，对流层延迟的误差在2.3～20m，利用现有各种数学模型可消除70%左右的电离层延迟，和90%—95%的对流层延迟[11]，因此，电离层与对流层延迟剩余量εi&t在17～47m。

由PDOP值的定义[12]

(27)

可得，伪距测量误差量对于定位精度的影响

Dp≈εi&t·PDOP

(28)

综合上述几点，得到单点最小二乘定位精度均值

(29)

给定误警率PFA可计算出相应地最大偏差量Tσ。

(30)

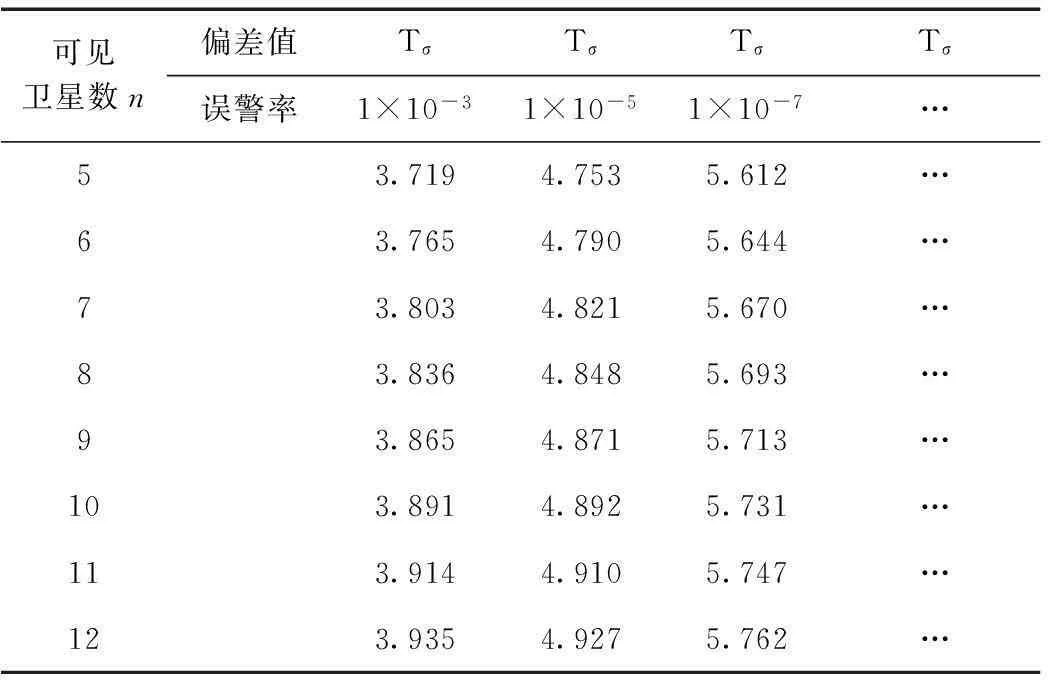
图5和表2表示了Tσ与误警率PFA的计算关系。

因此，阈值Tls的具体设置为

(31)

此外，对PDOP因子的研究表明，当PDOP<6时，用户导航定位线性方程是良性的，定位结果误差和伪距测量误差满足线性变化规律[13]。因此本方法只采用PDOP<6的定位结果，以保证其可用性。

图5　Tσ与误警率大小关系

可见卫星数n偏差值TσTσTσTσ误警率1×10-31×10-51×10-7…53.7194.7535.612…63.7654.7905.644…73.8034.8215.670…83.8364.8485.693…93.8654.8715.713…103.8914.8925.731…113.9144.9105.747…123.9354.9275.762…

3.2.2基于伪距残差的故障检测与排除

当部分可见卫星定位结果通过上述精度评估后，将利用其定位结果进行伪距残差计算，然后将各卫星的伪距残差量与故障判决门限值Td比较。大于Td的予以排除，小于Td的将参与最终的最小二乘定位解算。

下图为本方法的具体流程图见图6。

图6　算法流程

无故障假设H0：E(ri)=εpi， 则ri～N(εpi,σ2)

有故障假设H1：E(ri)≠εpi， 则ri～N(εpi+δi,σ2)

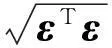
(32)

则检测阈值：

(33)

4性能对比测试与分析

4.1路测结果对比

本文分别对两种RAIM方法监测后接收机的最小二乘定位结果精度进行了对比分析。本次的测试数据来自于厦门岛内的一次路测数据(本次路测数据的粗差主要来源于基带芯片北斗通道跟踪环路在重捕获后的不稳定性引入的大粗差，以及城市峡谷的多径误差)，路测的路径包含了城市峡谷、短隧道、高架桥下。

从图7可以看出利用传统RAIM方法时，定位结果偏差很大，由上述的分析可知，当某颗卫星重捕获时(在城市峡谷中这种情况出现比较频繁)，由于基带芯片重捕获性能不佳，导致部分观测值中引入大的粗差，在此情形下传统的RAIM方法，利用了含有粗差观测值信息的先验接收机位置进行RAIM检测，从而使得良好的卫星观测值逐步被排除，如此循环导致最终参与定位的观测值数目偏少，从图7中坐标点样式可以看出：在定位结果误差较大的路段，定位坐标多呈现带菱形的定位点(图7、图8中定位点的形状与参与定位的卫星数目有关，空白的定位点代表参与定位的卫星数目大于5颗，带菱形的定位点代表参与定位的卫星数目少于5颗。)，并且一定概率下保留了含粗差的观测值，使得定位结果严重恶化。

对于图8可以看到，同一段数据，当使用本文所提出的方法进行RAIM监测时，最小二乘定位结果的精度有很大的改善。

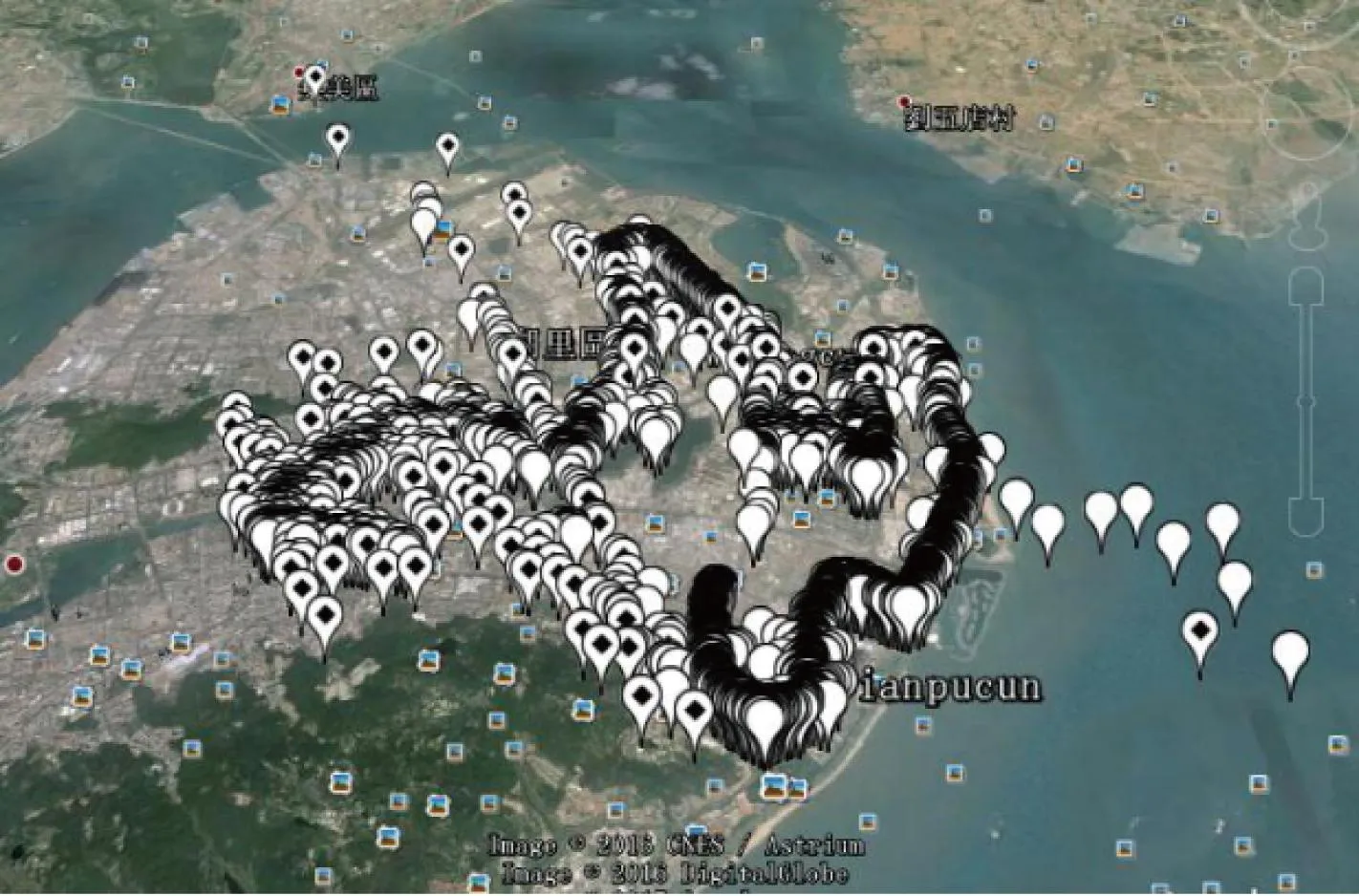
图7　传统RAIM方法下最小二乘定位结果

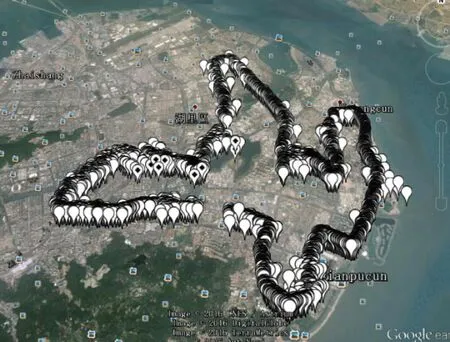
图8　本文所提RAIM方法下最小二乘定位结果

4.2故障检测率对比

对上述场景下截取一段840 s的实测数据进行故障标定，然后分别利用传统最小二乘残差法与本方法进行故障检测与排除(设定相同的误警率，此次实验误警率设置为10-5)，标记出所检测出的故障卫星。并与标定的故障进行对比，统计出两种方法对于故障卫星的检测率。

表3　故障检测率的对比

从上表可以看出，较之传统方法，而本文所提出的方法能更有效地检测出所有含粗差的故障卫星。

4.3定位精度对比

本文分别对两种RAIM方法监测后接收机的最小二乘定位结果精度进行了对比分析。

首先是x方向上的偏差对比。其中传统方法在x正方向上的定位偏差较大。偏差大于200 m的占10.48%，最大偏差达2 526.23 m，平均偏差134.04 m，而本方法，平均偏差46.61 m，99.88%的偏差在200 m以内。

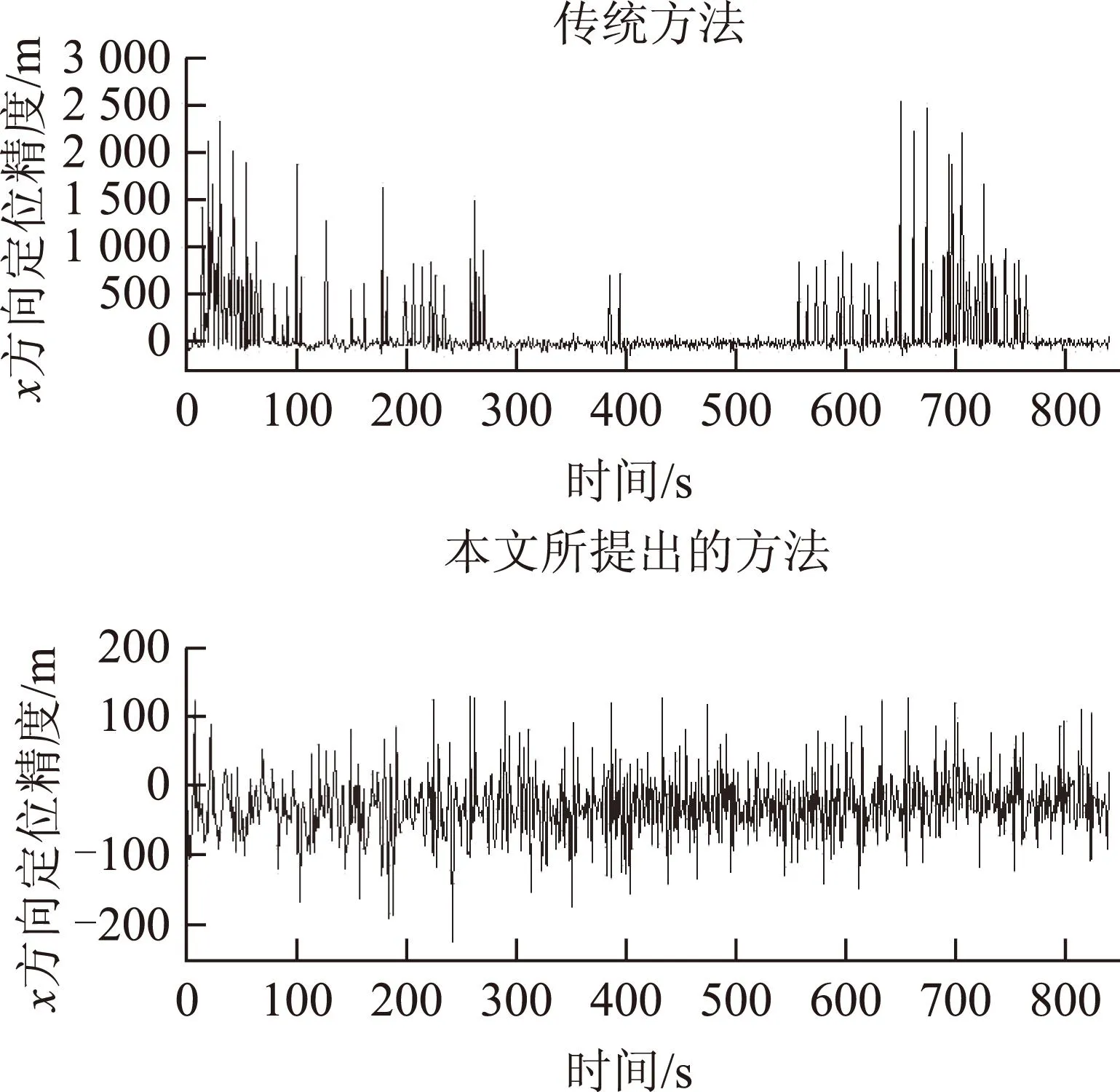
图9　x方向上的偏差对比

由图10可知，传统方法10.48%的偏差大于200 m，在y负方向最大偏差为3 558.63 m，平均偏差149.15 m，而本方法最大偏差为143.44 m，97.26%的偏差在100 m以内，平均偏差36.99 m。

图10　y方向上的偏差对比

由图11可得，在z方向上，传统方法最大偏差达2 097.39 m，6.55%的偏差大于200 m，平均偏差76.47 m，而本方法最大偏差为154.42 m，96.79%的偏差在100 m以内，平均偏差39.15 m。

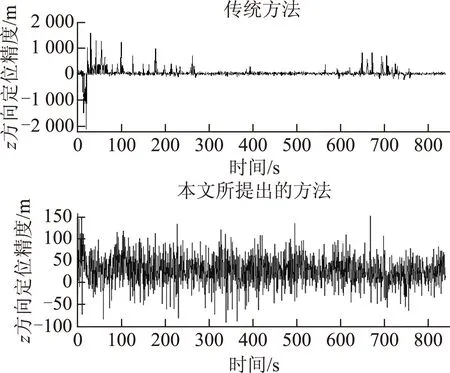
图11　z方向上的偏差对比

图12为三维偏差对比。其中传统方法10.95%的偏差大于200 m，最大偏差4 439.73 m，平均偏差230.22 m，而本方法最大偏差250.19 m，平均偏差80.44 m，仅有0.71%的定位结果偏差大于200 m。

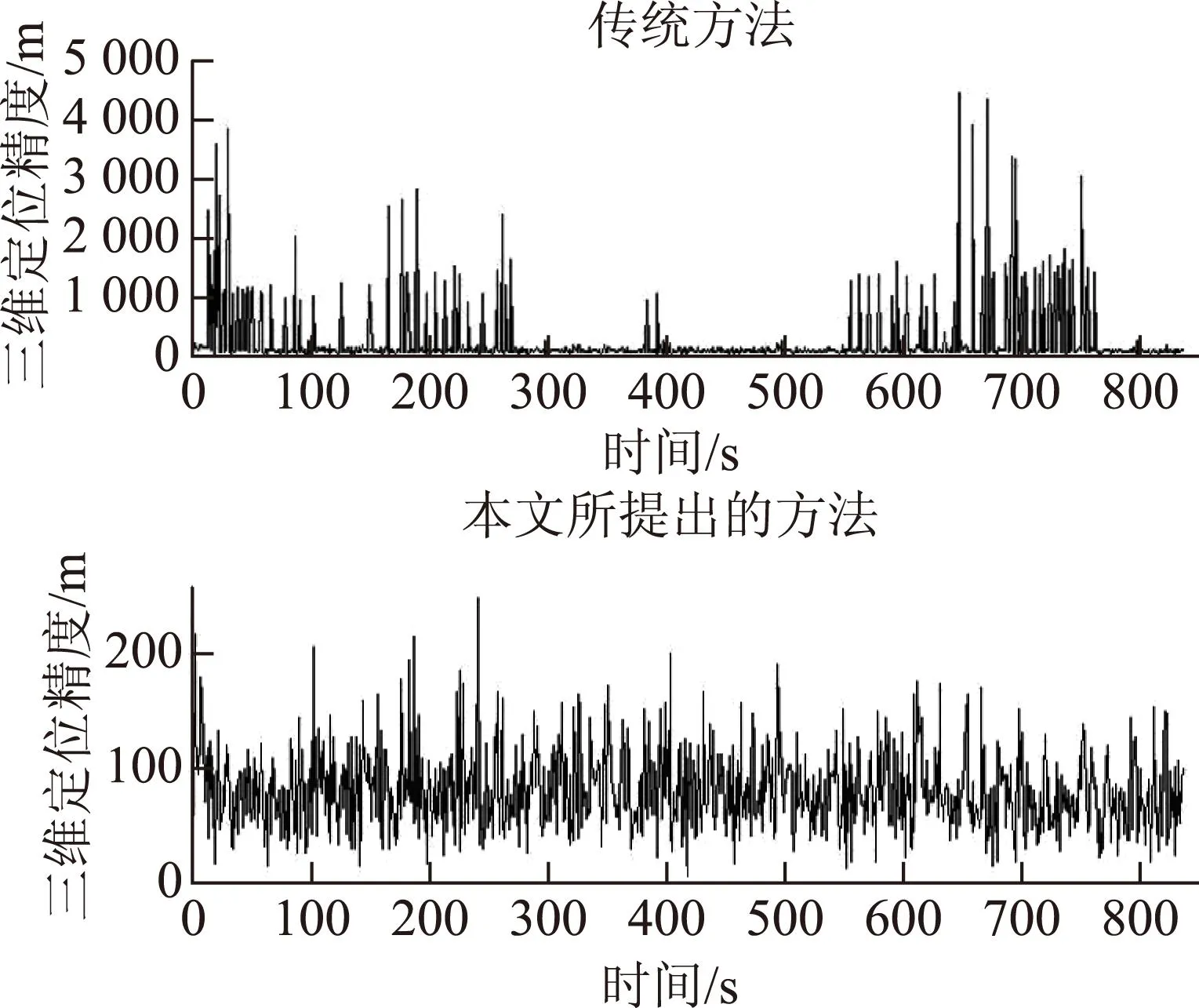
图12　三维偏差对比

5结束语

本文从实际问题出发，首先对传统方法进行了理论分析，指出了传统RAIM方法在无法获得较精确的接收机先验位置信息时，良好观测量被错误舍弃是可能的，尤其是在大的或者多个粗差观测值存在时。因此要提升基于伪距残差的RAIM算法的可用性和监测性能，关键在于要保证伪距残差量计算的精度。

并且本文推导了先验位置偏差与定位精度之间的数学关系，针对其在多粗差和大粗差场景下存在的上述问题提出了一种新的解决方法。较之传统方法，本方法利用最小均方中值结合自下而上的RAIM思想得到了有一定精度保障的接收机先验位置，然后进行伪距残差计算，因此一定程度上保证了在故障检测与识别时，各卫星伪距残差量的准确度，避免了传统方法所出现的问题。

经测试表明，新方法较传统方法能更有效在复杂场景下进行完好性监测，提高了接收机在复杂环境下的定位精度，和可用性。同时新方法通过自适应的检测阈值设置，进一步增强了此RAIM方法在不同环境下的适用性。当然，对于自适应的阈值设置还有一定改善空间，需进一步研究。

参考文献

[1]LEE Y C.Analysis of range and position comparison methods as a means to provide GPS integrity in the user receiver[C]//The Institute of Navigation.Proceedings of the ION 42nd Annual Meeting.Seattle，WA：The Institute of Navigation，1986：1-12.

[2]PARKINSON B W，AXELRAD P.Autonomous GPS integrity monitoring using the pseudo-range residual[J].Journal of the Institute of Navigation，1988，35(2)：255-274.

[3]STURZA M A.Navigation system integrity monitoring using redundant measurements[J].Journal of the Institute of Navigation，1988，35(4)：483-501.

[4]BROWN R G.A baseline GPS RAIM scheme and a note on the equivalence of three RAIM methods[J].Journal of the Institute of Navigation，1992，39(3)：301-316.

[5]PARKINSON B，SPILKER J，AXELRAD P，et al.Global positioning system：theory and applications[EB/OL].(1996-01-15)[2015-07-28].http://www.amazon.com/Global-Positioning-System-Applications-Astronautics/dp/156347106X.

[6]杨传森，卫星导航用户端自主完好性监测理论问题研究[D].南京：南京航空航天大学，2011.

[7]HAWKINS D.Identification of outliers[M].London：Chapman & Hall，1980.

[8]LU G.Quality control for differential kinematic GPS positioning[D].Calgary：University of Calgary，1991.

[9]ROUSSEEUW P J，LOY A M.Robust regression and outlier detection[M].New York：John Wiley & Sons，2003.

[10]蔡昌盛，李征航，张小红.SA取消前后GPS单点定位精度对比分析[J].测绘信息与工程，2002，27(3)：24-25.

[11]刘露强，纪元法，孙希延，等.电离层和对流层延迟对单频接收机定位的影响[J].桂林电子科技大学学报，2013，33(3)：196-199.

[12]邱致和，王万义.GPS原理与应用[M].北京：电子工业出版社，2002：187-211.

[13]帅平，曲广吉.卫星导航定位方程的病态条件[J].飞行器测控学报，2006，25(1)：1-5.

A Receiver Autonomous Integrity Monitoring Method Based on Positioning Result of Proportion of Visible Satellites

WUJie，PENGAo，SHIJianghong

(Department of Communication Engineering，Xiamen University，Xiamen 361005，China)

Abstract：The conventional receiver autonomous integrity monitoring algorithm of pseudo-range residual causes large residual error without a relatively accurate priori receiver position，which may lead to fault detection and identification.Therefore，measurements with gross errors may be used in positioning instead of high quality ones，especially when there are more than one measurement being distorted by gross errors.Meanwhile，the accuracy of the positioning result will be seriously deteriorated.In order to solve this problem，a new robust receiver autonomous integrity monitoring algorithm with positioning result based on the proportion of visible satellites is proposed in this paper.Using the proportion of visible satellites，the new algorithm produces a coarse position by the least squares method to calculate the pseudo-range residual.Accordingly，a robust approach to evaluate the accuracy of the coarse position based on the least median square is also proposed to make sure the position can meet the requirements of the following fault detection.In addition，the threshold mentioned in the new algorithm is derived theoretically.Finally，the performance of the new algorithm is good in simulations and real-data-tests，compared with conventional approaches.Results show that under the complicated scenarios the new algorithm can provide a considerable reduction of the probability of miss detection(7.89% in this test)，and improve the positioning accuracy remarkably.

Key words：receiver autonomous integrity monitoring；priori receiver position；pseudo-range residual；fault detection and fault identification；robust；least median square；proportion of visible satellites

中图分类号：P228

文献标识码：A

文章编号：2095-4999(2016)-01-0025-08

作者简介：第一吴杰(1990—)，男，湖南永州人，硕士生，主要从双模导航基带芯片算法研究。

基金项目：厦门市卫星导航研发中试基地资助项目(3502Z20121010)。

收稿日期：2015-09-21

引文格式：吴杰，彭敖，石江宏.基于部分可见星的接收机完好性监测方法[J].导航定位学报，2016，4(1)：25-32.(WU Jie，PENG Ao，SHI Jianghong.A Receiver Autonomous Integrity Monitoring Method Based on Positioning Result of Proportion of Visible Satellites[J].Journal of Navigation and Positioning，2016，4(1)：25-32.)DOI：10.16547/j.cnki.10-1096.20160106.