基于ARIMA模型的地球自转参数预报研究
2016-04-07叶修松
杨 杰,叶修松,曾 光,朱 俊
(1.宇航动力学国家重点实验室,西安 710043;2.西安卫星测控中心,西安 710043)
基于ARIMA模型的地球自转参数预报研究
杨杰1,2,叶修松1,2,曾光1,2,朱俊1,2
(1.宇航动力学国家重点实验室,西安710043;2.西安卫星测控中心,西安710043)
摘要:为了提高基于ARIMA模型的地球自转参数预报精度,着重分析了ERP数据序列预处理中周期项成分的精确获取技术、ARMA模型阶次的优化选择问题,以及ERP数据序列不同差分次数对模型精度的影响。利用国际地球自转和参考系统服务组织公布的ERP最终产品,365组预报结果表明,UT1-UTC预报30 d精度可达3.398 6 ms,10 d以内预报应选取2次差分模型,10 d以上选取1次差分模型;日长预报30 d精度可达0.337 5 ms,应选取零次差分预报模型;Xp预报30 d精度为11.189 1 mas,Yp预报30 d精度为7.932 1 mas,两者均选择1次差分模型。
关键词:差分自回归滑动平均模型;地球自转参数预报;差分;模型阶次;优化
0引言
地球定向参数是连接天球和地球参考框架的关键参数,是卫星导航应用的关键因素,广泛应用于卫星、飞船及空间飞行器的地基测定轨、地面点或船只的定位、弹道导弹的轨道设计、目标的瞄准发射以及来犯导弹的拦截、空基定位的飞行器星下点坐标的测定和对地姿态的测控等方面。同时,地球定向参数也是天文地球动力学、天体测量学、地球物理学和大地测量学研究的最主要观测量和基础科学数据,为研究地球自转变化的机制、板块运动、固体潮及地球内部结构等地球动力学问题提供了极大的便利,也是研究地球整体旋转、表面物质运动、大气环流变化甚至地质灾害预报的基础信息,极大推动了天文地球动力学的发展[1]。
20世纪60年代以来,甚长基线干涉、激光测卫、全球定位系统等现代大地测量技术的快速发展,极大地提高了地球定向参数的观测精度。以国际地球自转和参考系统服务组织(International Earth Rotation and Reference Systems Service,IERRSS)为代表的国际组织机构定期发布精确的地球自转参数(Earth rotation parameters,ERP),但无法适应精密大地测量、航天测控工程等领域的实时应用,为此需要利用IERRSS的预报产品或基于IERRSS的解算数据开发自主的ERP预报产品。常见的ERP预报算法有最小二乘法、协方差分析法、神经网络法、自回归滑动平均法、小波分析法、卡尔曼滤波法,以及其他组合预报法等[2-9]。
采用差分自回归滑动平均模型(auto-regressive integrated moving average,ARIMA)对ERP参数进行外推预报。为使预处理后的ERP更符合自回归滑动平均(auto-regressive moving average,ARMA)模型对随机过程的要求,可从2个方面进行分析:①对数据序列进行精确的频谱分析,获取准确的周期项成分;②差分ERP数据序列以使其满足随机过程的要求。此外,为了提高ARMA模型的预报精度,需要选取合适的模型阶次,可通过数据序列的自吻合误差确定最优的模型阶次。在开发ERP预报产品时,可通过比较不同差分次数对测试样本数据序列预报精度的影响以选择合适的差分预报模型。
1ERP预报流程

图1 UT1-UTC的预报算法

图2 日长和极移的预报算法
ERP预报的主要流程见图1和图2[10],主要包含预测模型的建立和外推估计,针对大气角动量和海洋角动量建模复杂的特点,在预报过程中先不予考虑。在预测模型建立过程中,针对周日变化,需要减去跳秒、潮汐、UT2-UT1、趋势项和周期项成分等,而日长(length of day,LOD)和极移参数预测模型的建立则相对简单,仅需进行趋势项和周期项成分的分离。针对预处理后的ERP,需要进一步进行差分运算,以获取满足ARMA模型特性的数据时间序列,再进行ARMA模型参数估计和外推预测。
为了使预处理后的ERP数据序列满足ARMA模型的特性要求,需要充分剔除数据序列中的周期项。同时,可通过差分数据序列进一步提高ERP数据序列预处理的精度。图1和图2中的最小二乘模型表示为

(1)
式(1)中,ωi表示ERP数据序列中的周期项频率,比如钱德勒周期项和年周期项等。
2ARIMA模型的预报算法
ARIMA模型预报算法的主要流程如图3所示[11]
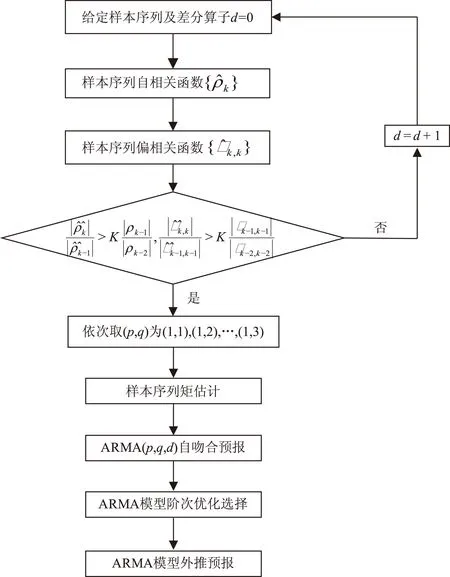
图3 ARIMA模型预报算法
针对图3中的预报流程,主要解决3个技术问题,即ERP数据序列的差分次数、ARMA模型的阶次选择、ERP数据序列不同差分次数的预报精度等。图3中,各个环节的计算过程表示如下。
2.1样本自相关和偏相关函数的计算
给定样本序列{X1,X2,…,XN}, 自相关和互相关函数计算结果分别表示为
(2)
(3)
2.2ARIMA模型参数的矩估计
Step 1:自回归参数向量φ的矩估计结果为
(4)
Step 2:向量Xt=Xt-φ1Xt-1-…-φpXt-p自协方差函数的矩估计结果表示为
(k=0,1,2,…,q)
(5)
Step3:滑动平均系数向量θ的矩估计结果为
(6)
2.3ARIMA模型不同差分阶次预报算法
2.3.1直接预报
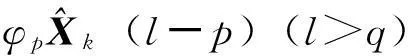
(7)
(8)
2.3.2差分预报
差分后的序列预报结果见式(6)和式(7),那么,一次差分预报结果为
(9)
二次差分预报结果为
(10)
2.3.3ARMA(p,q)序列格林函数的计算
格林函数计算过程表示为
(11)
结合式(11),针对不同的模型阶次组合,格林函数计算过程分别表示为
1)ARMA(1,1)模型及其格林函数表示为
Xt-φ1Xt-1=at-θ1at-1
(12)
(13)
2)ARMA(1,2)模型及其格林函数表示为
Xt-φ1Xt-1=at-θ1at-1-θ2at-2
(14)
(15)
3)ARMA(1,3)模型及其格林函数表示为
Xt-φ1Xt-1=at-θ1at-1-θ2at-2-θ3at-3
(16)
(17)
4)ARMA(2,1)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2=at-θ1at-1
(18)
(19)
5)ARMA(2,2)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2=at-θ1at-1-θ2at-2
(20)
(21)
6)ARMA(2,3)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2=at-θ1at-1-θ2at-2-θ3at-3
(22)
(23)
7)ARMA(3,1)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2-φ3Xt-3=at-θ1at-1
(24)
(25)
8)ARMA(3,2)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2-φ3Xt-3=at-θ1at-1-θ2at-2
(26)
(27)
9)ARMA(3,3)模型及其格林函数表示为
Xt-φ1Xt-1-φ2Xt-2-φ3Xt-3=
at-θ1at-1-θ2at-2-θ3at-3
(28)
(29)
3ERP数据序列频谱分析结果
利用IERRSS最终公布的2000年~2012年的数据序列,通过快速傅立叶变换(fast Fourier transformation,FFT)变换对去除趋势项后的各参数序列进行频谱分析,求取ERP序列中的周期项频谱分量,结果表示如下。
3.1UT1-UTC频谱分析结果
UT1-UTC频谱分析结果见图4。

图4 UT1-UTC频谱分析结果
根据图4获取的UT1-UTC时间序列周期信号频谱分量见表1。
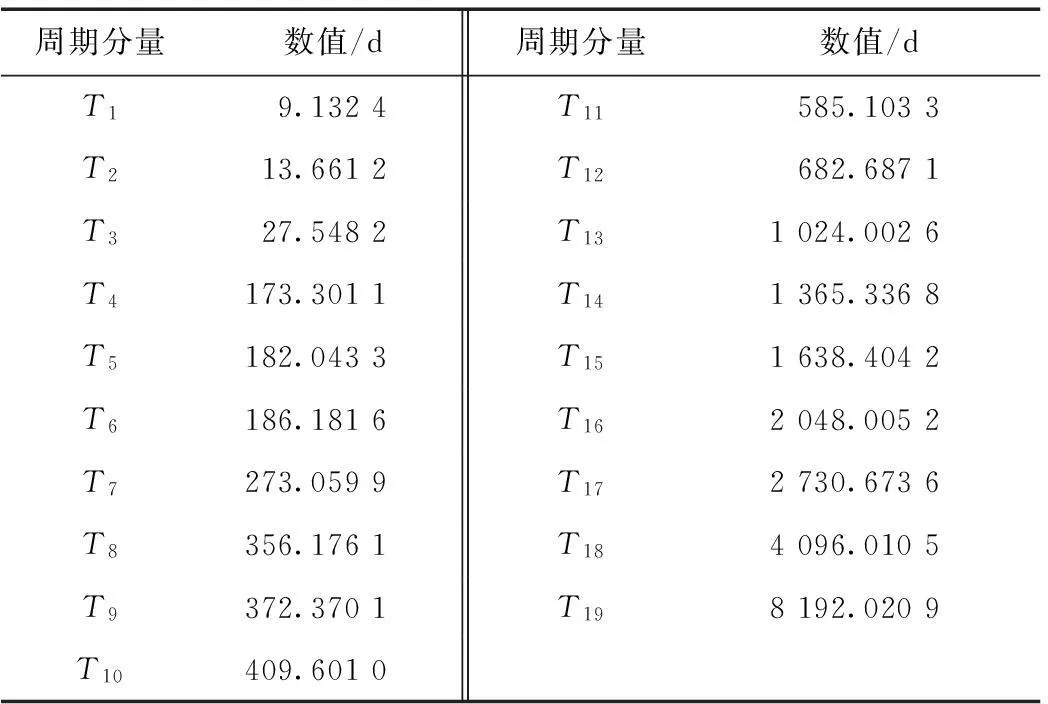
表1 UT1-UTC序列周期项
根据表1可知,UT1-UTC序列中的周期分量不仅包含钱德勒周期、0.5 a、1 a周期项,还包括其它高频低频周期项。
3.2LOD频谱分析结果
LOD频谱分析结果见图5。

图5 LOD频谱分析结果
根据图5获取的LOD时间序列周期信号频谱分量见表2。

表2 LOD序列周期项
根据表2可知,LOD序列中的周期分量不仅包含钱德勒周期、0.5 a、1 a周期项,还包括其它高频低频周期项。
3.3Xp及Yp频谱分析结果
Xp及Yp频谱分析结果见图6和图7。

图6 Xp频谱分析结果

图7 Yp频谱分析结果
根据图6和图7获取的极移序列周期信号频谱分量见表3。

表3 Xp及Yp序列周期项
根据表3可知,极移序列中的周期分量主要为钱德勒周期和1 a周期项。
4ARMA模型阶次优化选择及ERP预报精度分析
采用2000年~2012年的数据序列,训练样本共4 565个数据,采用滑动窗口的方式,每组训练样本数据序列分别预报30 d的ERP参数,共统计365组预报结果。每组预报误差为30 d误差绝对值的最大值。
每组训练样本在ARMA模型参数矩估计中,模型阶次(p,q)依次取为(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),选取每组训练样本自拟合误差的最小偏差为评价准则进行模型阶次优化选择。这里,仅给出前30组UT1-UTC数据序列的最优阶次,见表4。
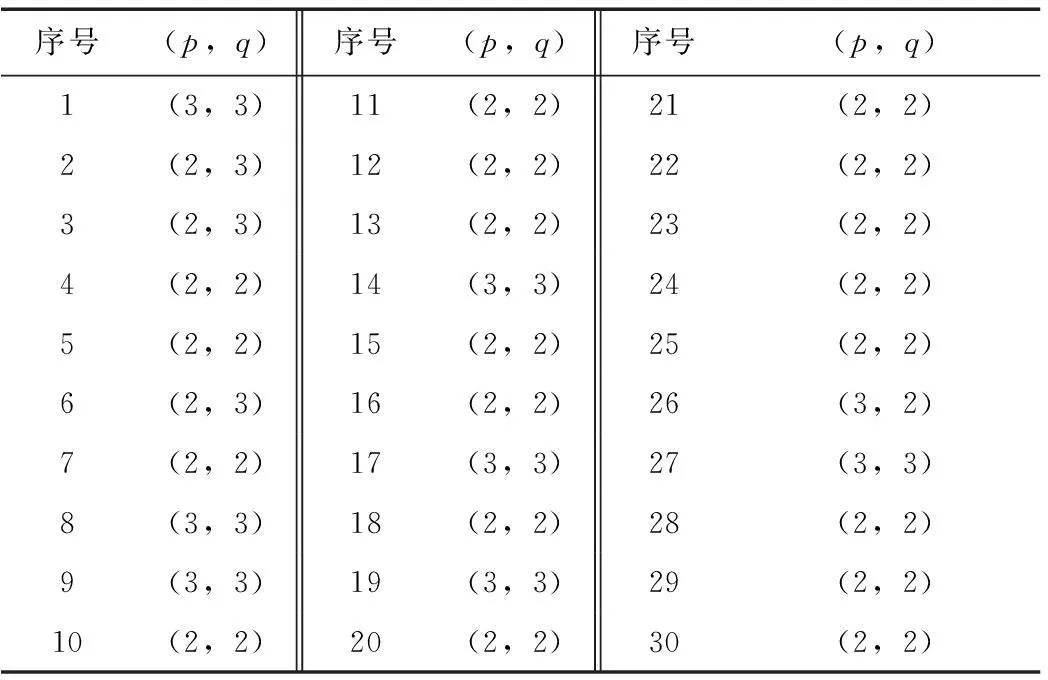
表4 前30组UT1-UTC数据序列ARMA模型最优阶次
4.1UT1-UTC预报结果
零次差分预报结果较差。这里仅给出1次和2次差分预报30 d UT1-UTC的365组预报误差分布和平均预报误差,见图8和图9。
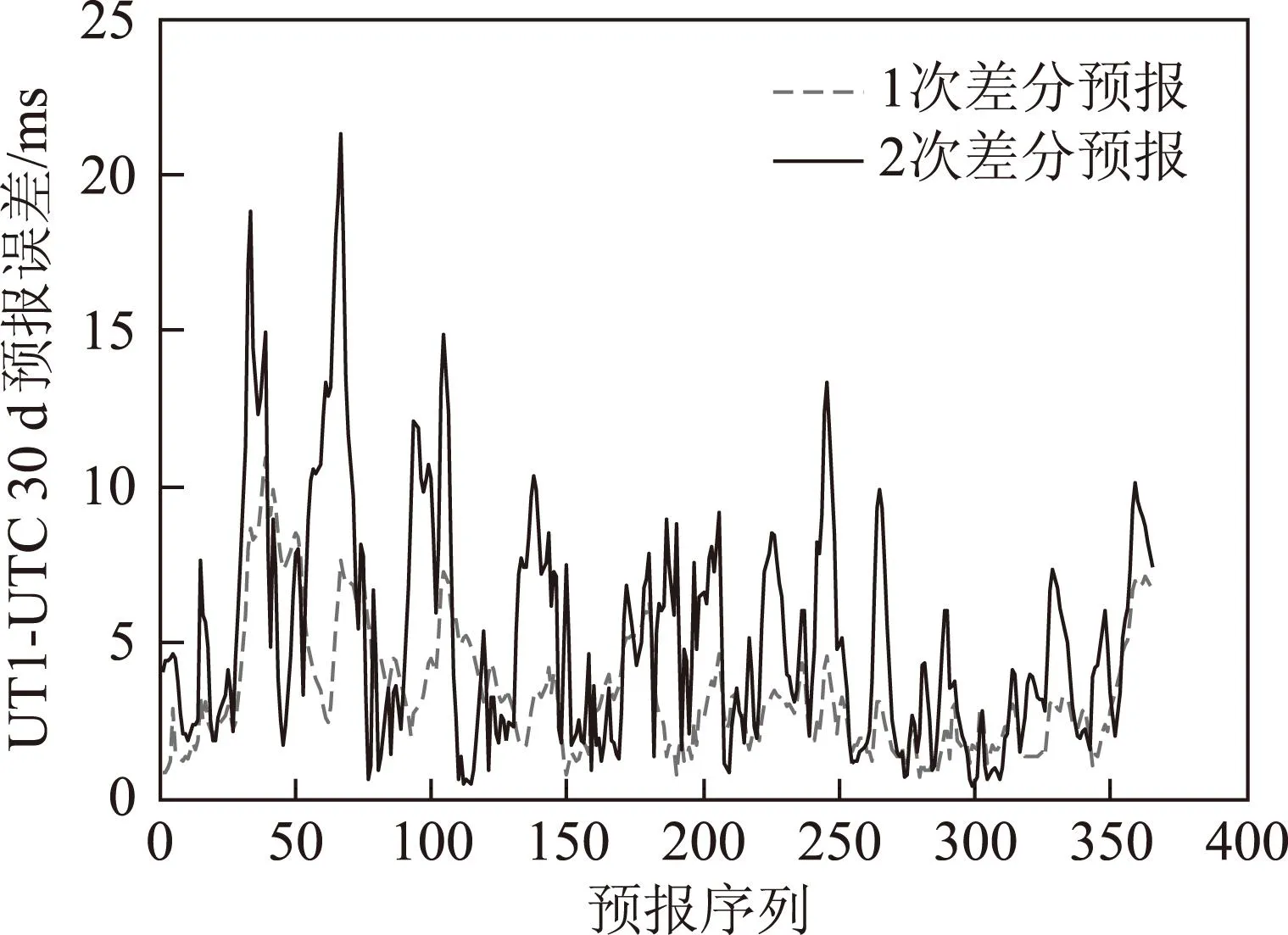
图8 UT1-UTC差分预报误差分布
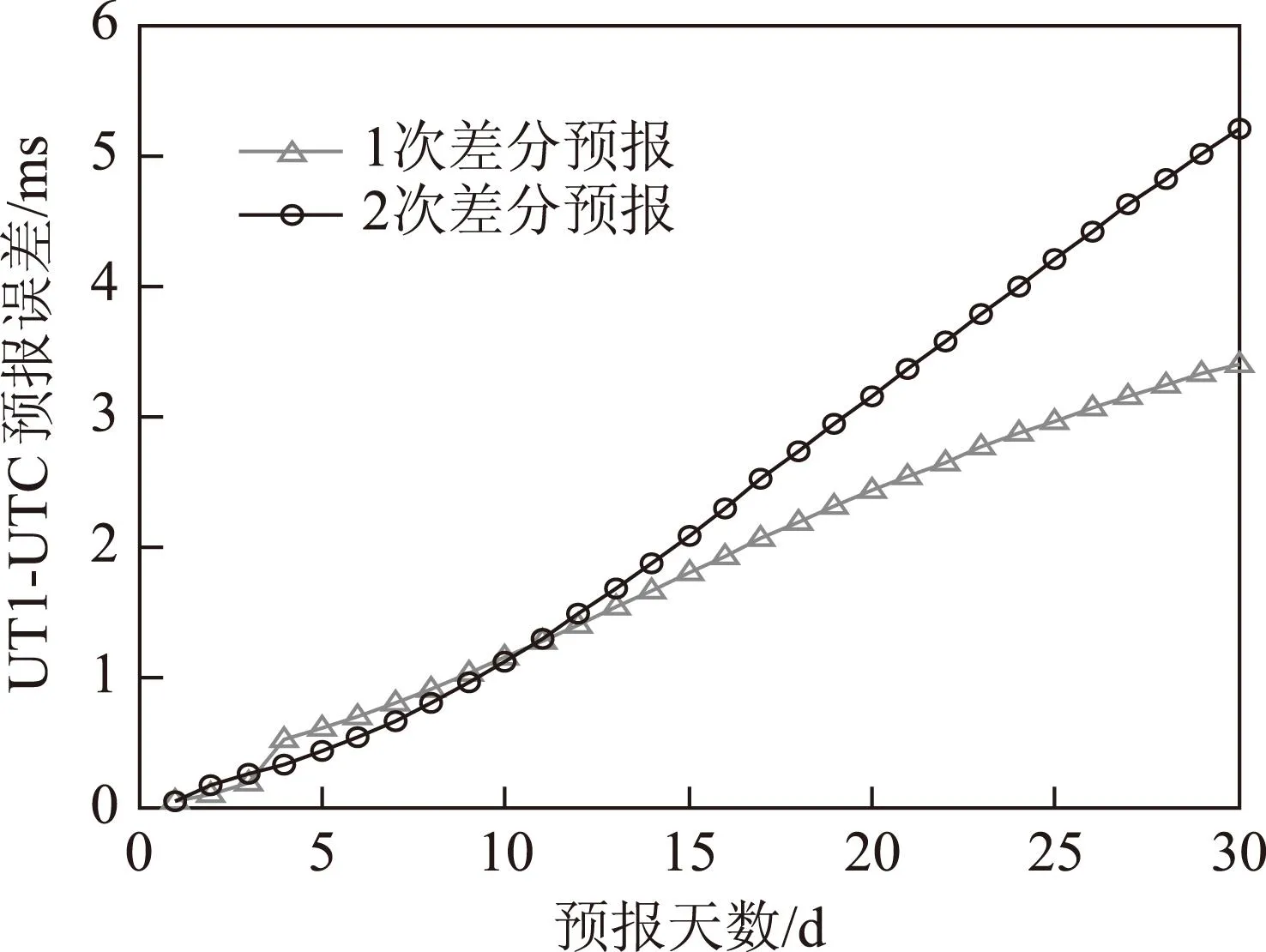
图9 UT1-UTC差分预报平均误差
根据图8和图9可知,UT1-UTC的5 d最好预报结果为0.427 ms,10 d为1.117 ms,30 d为3.399 ms。当预报天数小于10 d时,二次差分精度略高;当预报天数大于10 d时,一次差分预报精度明显高于二次差分。
4.2LOD预报结果
这里给出不同差分次数预报30 d LOD的365组预报误差分布和平均预报误差,见图10和图11。

图10 LOD差分预报误差分布

图11 LOD差分预报平均误差
根据图10和图11可知,LOD的5 d最好预报结果为0.134 ms,10 d为0.205 ms,30 d为0.338 ms。零次差分预报精度略优于一次差分,明显优于二次差分。
4.3Xp预报结果
零次差分预报结果较差。这里仅给出1次和2次差分预报30 dXp的365组预报误差分布和平均预报误差,见图12和图13。
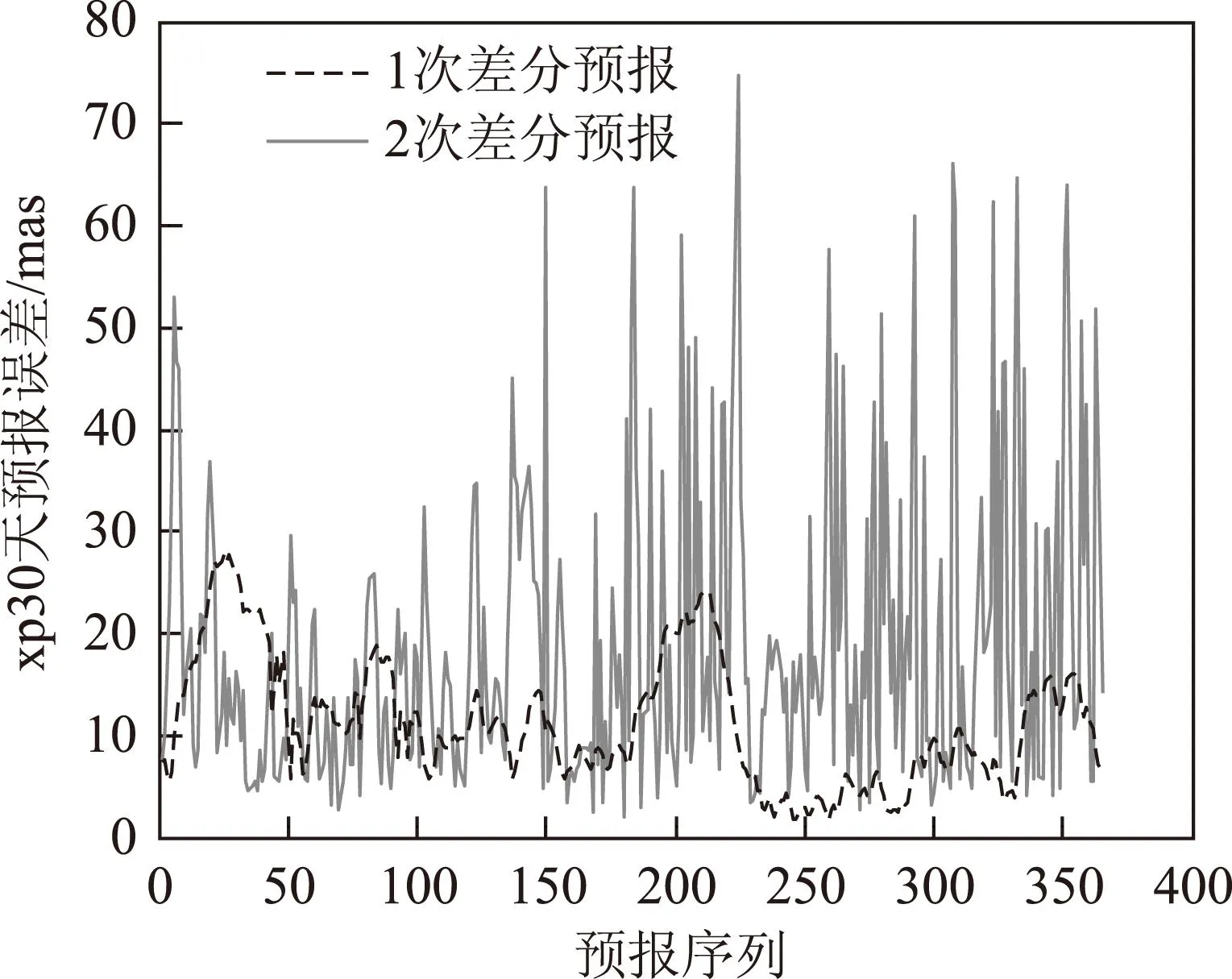
图12 Xp差分预报误差分布
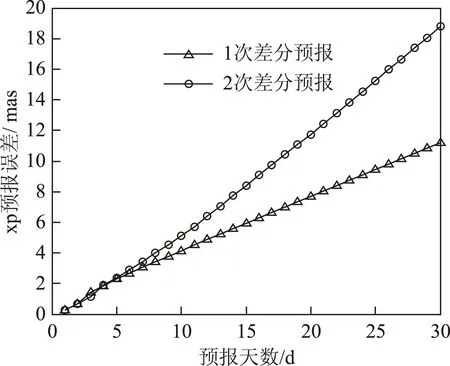
图13 Xp差分预报平均误差
根据图12和图13可知,5 dXp最好的预报结果为2.287 mas,10 d为5.941 mas,30 d为11.189 mas。预报天数小于5 d时,2种差分模型预报精度相当;预报天数大于5 d时,零次差分预报精度较差,一次差分预报精度明显优于二次差分。
4.4Yp预报结果
零次差分预报结果较差。这里仅给出1次和2次差分预报30 dYp的365组预报误差分布和平均预报误差,见图14和图15。
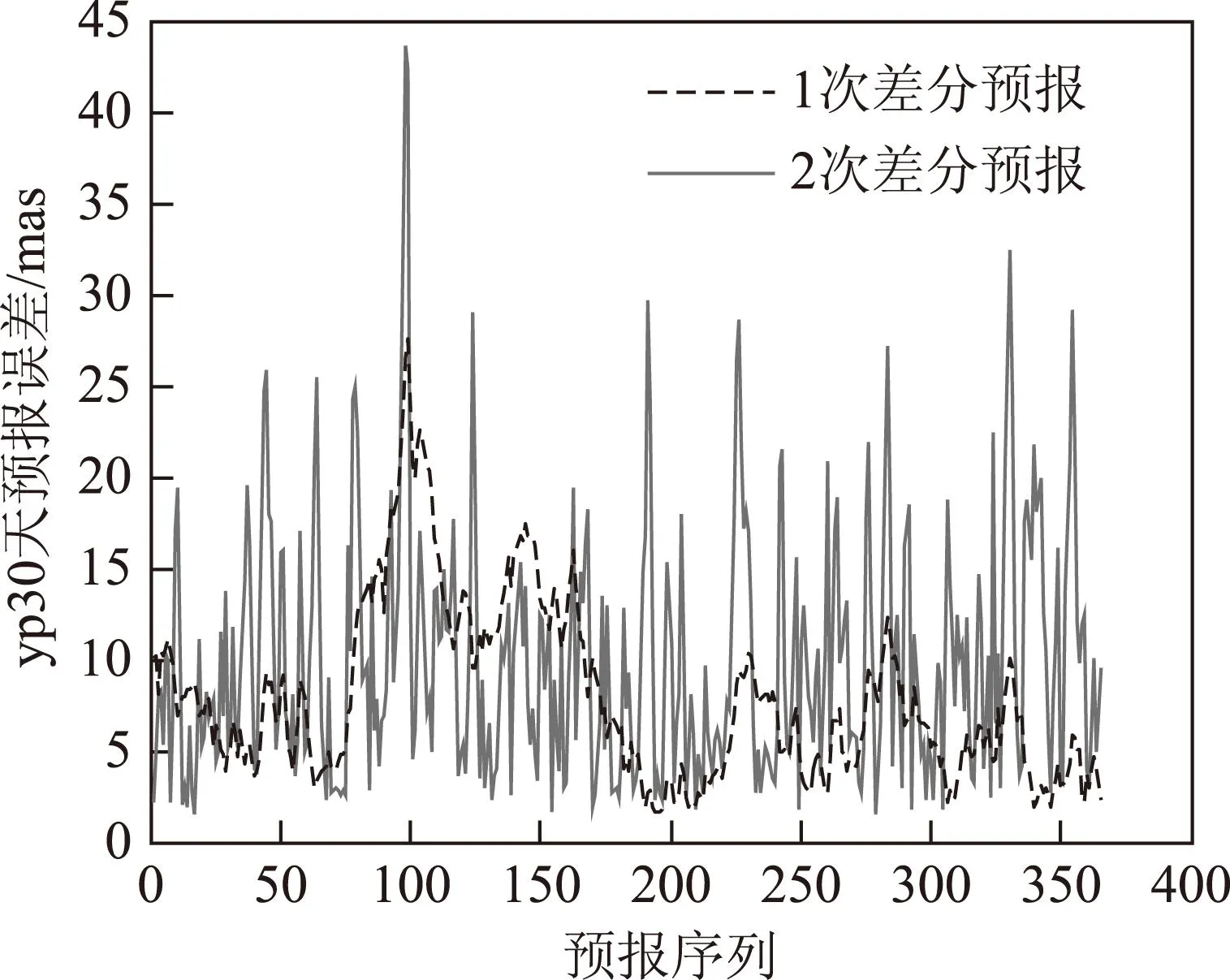
图14 Yp差分预报误差分布
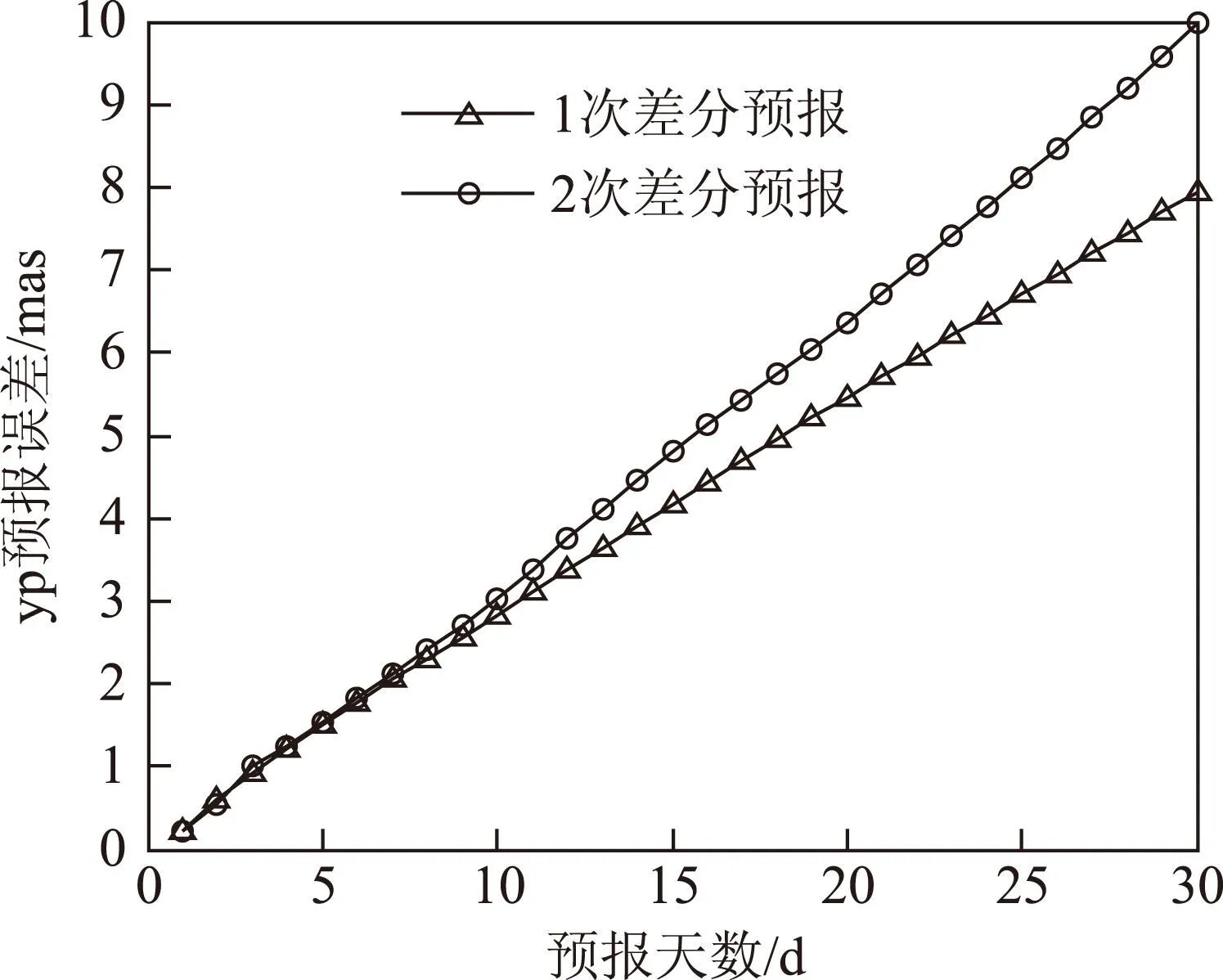
图15 Yp差分预报平均误差
根据图14和图15可知,5 dYp最好的预报结果为1.506 mas,10 d为2.765 mas,30 d为7.852 mas。预报天数小于5 d时,2种差分模型预报精度相当;预报天数大于5 d时,零次差分预报精度较差,一次差分预报精度明显优于二次差分。
5结束语
本文分析了ARIMA模型预报的3项关键技术。分别研究了ERP数据序列中周期项成分的精确获取问题、ERP模型阶次的优化问题,以及不同差分次数对ERP预报精度的分析。为此,可得到如下结论:
1)训练样本数据序列的频谱分析可准确获取周期项成分,从而使得预处理后的ERP数据序列具有更符合ARMA模型要求的随机过程特性。
2)训练样本数据序列的最小自拟合误差均方差可建立模型阶次优化选择的评价准则。
3)测试样本数据序列的最小预报误差有利于模型差分次数的优化选择,可用于不同天数ERP预报产品的开发。
4)通过上述分析方法可知,30 d UT1-UTC的预报精度为3.399 ms,30 d LOD预报精度为0.338 ms,30 dXp预报精度为11.189 mas,30 dYp预报精度为7.852 mas。
致谢:作者感谢国际GNSS监测评估系统(iGMAS)提供的观测数据(www.igmas.org)。
参考文献
[1]郑大伟,虞南华.地球自转及其和地球物理现象的联系:I日长变化[J].地球物理学进展,1996,11(2):34-37.
[2]AKAIKE H.Utoregressive model fitting for control[J].Annals of the Institute of Statistical Mathematics,1971,23(1):162-180.
[3]BARNES R T H,HIDE R,WHITE A A,et al.Atmospheric angular momentum fluctuations,length-of-day changes and polar motion[C]//Royal Society.Proceedings of Mathematical and Physical Sciences.London,UK:Royal Society,1983:31-73.
[4]HAMDAN K,SUNG L Y.Stochastic modeling of length of day and universal time[J].Journal of Geodesy,1996,70(1):307-320.
[5]KOSEK W,MCCARTHY D,LUZUM B J.Possible improvement of Earth orientation forecast using autocovariance prediction procedures[J].Journal of Geodesy,1998,72(12):189-199.
[6]GROSS R,EUBANKS T M,STEPPE J A.A Kalman filter-based approach to combining independent Earth-orientation series[J].Journal of Geodesy,1998,72(9):215-235.
[7]SCHUH H,ULRICH M,EGGER D,et al.Prediction of Earth orientation parameters by artificial neural networks[J].Journal of Geodesy,2002,76(3):247-258.
[8]JOHNSON T,LUZUM B J,RAY J R.Improved near-term Earth rotation predictions using atomospheric angular momentum analysis and forecasts[J].Journal of Geodesy,2005,79(6):209-221.
[9]HUBER P J.Modeling the length of day and extrapolating the rotation of the Earth[J].Journal of Geodesy,2006,80(12):283-303.
[10]NIEDZIELSKI T,KOSEK W.Prediction of UT1-UTC,LOD and AAM χ3 by combination of least-squares and multivariate stochastic methods[J].Journal of Geodesy,2008,82(2):83-92.
[11]BROCKWELL P J,DAVIS R A.Introduction to time series and forecasting[M].New York,USA:Springer,1979:212-220.
Research of the ARIMA-based Prediction of Earth Rotation Parameters
YANGJie1,2,YEXiusong1,2,ZENGGuang1,2,ZHUJun1,2
(1.State Key Laboratory of Astronautic Dynamics,Xi’an 710043,China;2.Xi’an Satellite Control Center,Xi’an 710043,China)
Abstract:Some critical problems are successfully resolved to improve the Earth rotation parameters (ERP) prediction accuracy based on the auto-regressive integrated moving average (ARIMA) model,which are the precise extraction of periodic components in the ERP,the order optimization of ARIMA model and the effects of model order on the ERP prediction accuracy.The prediction experiments are implemented on the final ERP products released by the International Earth Rotation and Reference Systems Service (IERRSS).Some key conclusions can be drawn from the total 365 groups of prediction results.Firstly,the 30-day prediction error of UT1-UTC is 3.398 6 ms.The two-order difference model can be selected for the prediction in less than 10 d,but the one-order difference model is selected for the prediction in more than 10 d.Secondly,the 30-day prediction error of length of day (LOD) is 0.337 5 ms and the difference model order is zero.Finally,the 30-day prediction error is 11.189 1 mas and 7.932 1 mas for the x-axis and y-axis component of polar motion respectively.Additionally,the difference model order is one for the above two cases.
Key words:auto-regressive integrated moving average model;Earth rotation parameters prediction;difference;model order;optimization
中图分类号:P228
文献标识码:A
文章编号:2095-4999(2016)-01-0068-08
作者简介:第一杨杰(1985—),男,山西运城人,工程师,博士,现主要从事航天器精密定轨和定位方面工作。
收稿日期:2015-06-15
引文格式:杨杰,叶修松,曾光,等.基于ARIMA模型的地球自转参数预报研究[J].导航定位学报,2016,4(1):68-74,87.(YANG Jie,YE Xiusong,ZENG Guang,et al.Research of the ARIMA-based Prediction of Earth Rotation Parameters[J].Journal of Navigation and Positioning,2016,4(1):68-74,87.)DOI:10.16547/j.cnki.10-1096.20160114.
