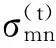基于扩展卡尔曼滤波的动态协同定位算法
2016-04-07柯明星童凯翔
柯明星,吕 晶,童凯翔,朱 明
(1.解放军理工大学 通信工程学院,南京 210007;2.卫星通信与导航江苏高校协同创新中心,南京 210007)
基于扩展卡尔曼滤波的动态协同定位算法
柯明星1,2,吕晶1,2,童凯翔1,2,朱明1,2
(1.解放军理工大学 通信工程学院,南京210007;2.卫星通信与导航江苏高校协同创新中心,南京210007)
摘要:卫星导航系统是目前应用最为广泛的一种定位与导航系统,然而在城区、峡谷、森林等复杂条件下其所提供的定位与导航性能会下降甚至无法提供服务。针对该问题,已经有多种卫星导航增强手段被提出,其中,用户间的协同定位由于可以减轻对基础设施的依赖,具有很大发展前景。本文提出了基于扩展卡尔曼的协同定位算法,建立了动态条件下用户的位置速度矢量模型的系统方程,利用该算法在动态协同定位系统中实现对用户的位置和速度的估计。文中论述了算法的详细过程,并通过计算机软件实时产生卫星的三维位置,构建了一个动态用户协同定位场景。数值仿真结果表明,该算法能够有效地估计出用户的位置和速度。
关键词:扩展卡尔曼滤波;协同定位;动态系统;性能估计
0引言
目前,位置信息已经在军事、海事、搜救等很多领域起着不可或缺的作用。全球导航卫星系统(global navigation satellite system,GNSS)是目前应用最为广泛的一种定位与导航系统。然而,在一些封闭场景,比如峡谷、森林或是存在城市建筑物遮挡情况下,GNSS就不能保证服务的质量甚至不能提供定位服务。
针对这类问题,有多种导航增强手段被提出,如传统的星基导航增强、基于伪卫星的导航增强、辅助全球导航卫星系统以及组合导航等[1]。协同定位是目前卫星导航定位领域比较新颖而且有效的解决方法,其由于可以减轻对基础设施的依赖而显现出了很大吸引力。协同定位的概念最早是在1996年由日本学者在机器人定位领域提出[2],后来在无线传感网领域成为一个热门的研究方向[3]。在卫星导航定位领域,有关协同技术的研究主要集中在对一些简单模型用户协同定位精度和覆盖范围等性能增强的验证,主要的的研究成果有发表在文献[4-5]中。利用协同来解决实际问题的关键是协同算法可以执行分布式计算并收敛。定位问题本质上可以看做状态估计的问题。最优状态估计在很多领域都获得了广泛的应用,典型的方法有最小二乘估计,卡尔曼滤波,粒子滤波等[6]。其中卡尔曼滤波作为动态系统状态估计经典方法,一经提出便在精确制导、数据通信、全球定位、目标跟踪等领域受到了广泛关注。但是,卡尔曼滤波的局限性是要求估计系统为线性,而卫星导航定位中相对应的系统估计方程是非线性方程。对此,将卡尔曼滤波改进得到扩展卡尔曼滤波后才能更好的应用于卫星导航定位中。扩展卡尔曼滤波是通过对非线性函数的泰勒级数展开进行一阶线性化截断,忽略其余高阶项,从而将非线性化问题线性化。
本文通过引入基于扩展卡尔曼滤波的协同定位算法来提高GNSS定位的精度与可用性。构建了动态条件下用户的协同定位模型,实现了对模型中用户的位置和速度状态的有效估计。
文章各章节安排如下:第一部分为动态场景的建立,得到系统模型和观测模型;第二部分为扩展卡尔曼滤波算法的简介;第三部分为协同定位算法的描述并将其应用于该具体场景;仿真结果出现在第四部分;第五部分对全文进行总结。
1动态场景介绍
1.1场景描述
本文所关注的动态协同定位网络如图1所示。场景中一共存在6个用户,以符号m1~m6表示,对于每个用户而言,与其他用户协同关系的存在以连线表示,每个用户可见星如表1所示。例如,对于m1而言,用户m2、m5、m6能与其协同,可见星为S1、S2、S3、S4、S5、S6、S7号星。对用户而言,其所能观测到的卫星集合以Sm表示,所有的协同用户的集合以Mm表示。
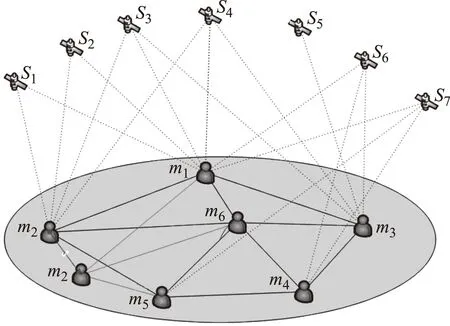
图1 协同网络场景示意图
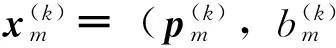
通常在GNSS系统中,要想确定一个用户的位置坐标信息,起码需要四颗可见卫星,因而在上图所示场景中,只有用户m1、m2、m3可以定位。但是经过用户间的协同之后,可以得到所有用户的位置信息,甚至有些用户在一颗星都不可见的情况下,如用户m6,也能够得到其比较精确的位置速度估计信息。
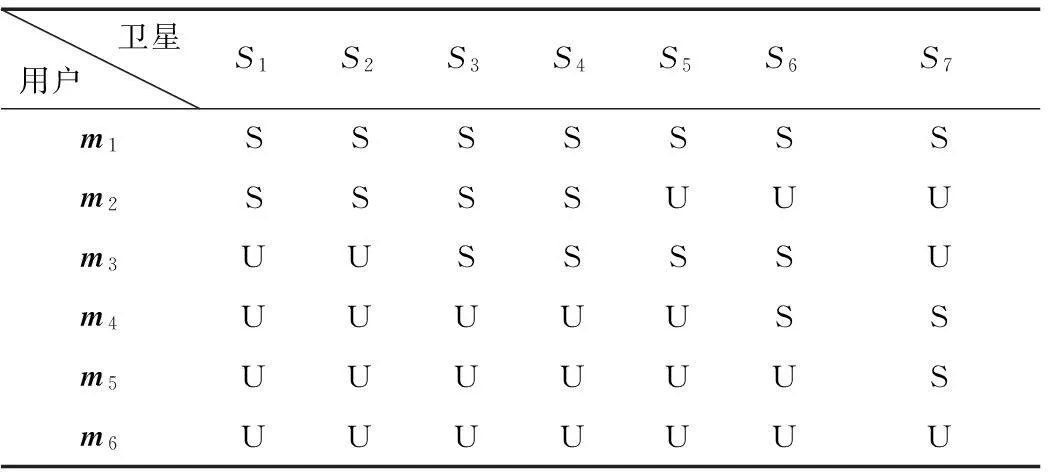
表1 各个用户可见星(S表示可见,U表示不可见)
1.2系统模型
该系统的状态方程为
(1)
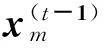
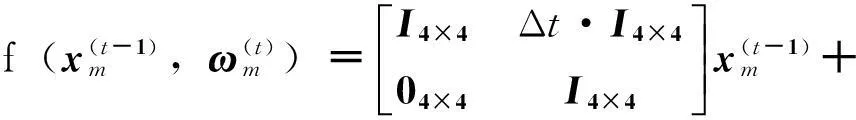
(2)
(3)
式(2)中,I表示4×4的单位阵,Δt表示的是信息更新的时间间隔。
1.3观测模型
用户的观测量为来自卫星的伪距测量和来自协同用户的距离测量。观测模型为
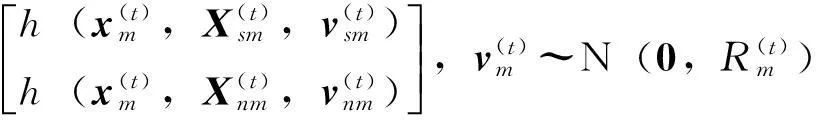
(4)
(5)
在t时刻,用户m与卫星s之间的伪距为
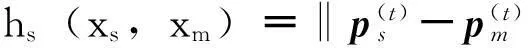

(6)
得出扩展卡尔曼中所需的雅克比矩阵为
(7)
在t时刻,用户与用户之间的距离测量为

(8)

2扩展卡尔曼滤波法
扩展卡尔曼滤波的思想是用线性化的方法来近似非线性化模型。它是一种迭代算法,根据噪声的统计特性和当前的测量值对用户的状态做出最佳的估计。滤波器主要分为两步:预测过程和更新过程。
2.1预测过程
预测过程即利用t-1时刻的状态量和协方差去估计t时刻的状态量和协方差,这里用函数f(·)表示状态预测函数为
(9)
(10)
2.2更新过程
(11)
(12)
求卡尔曼增益
(13)
更新状态估计
(14)
(15)
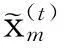
3协同定位算法
3.1协同定位基本原理
用户之间的协同,通过用户与用户的通信和测距来实现。用户之间相互通信,相互之间可以交互获取所需信息。在本文的模型中,用户之间交换的是位置坐标信息。而通过测距进行协同,用户得到其与邻近用户的距离信息,距离信息可以加入定位方程组进行求解,不仅能够提高定位的精度,还能使一些原本不能定位的系统实现定位,提高了用户的可定位性。
3.2基于扩展卡尔曼的协同定位算法流程
基于扩展卡尔曼滤波的协同定位算法流程
前提:卫星的状态是已知的,用户运动状态为匀速直线运动;
4:获取观测量,列出系统的状态转移方程和观测方程,计算雅克比矩阵H(t);
5:计算中间矩阵S(t)m和观测量与预测量的偏差ΔZ,得到卡尔曼增益K;
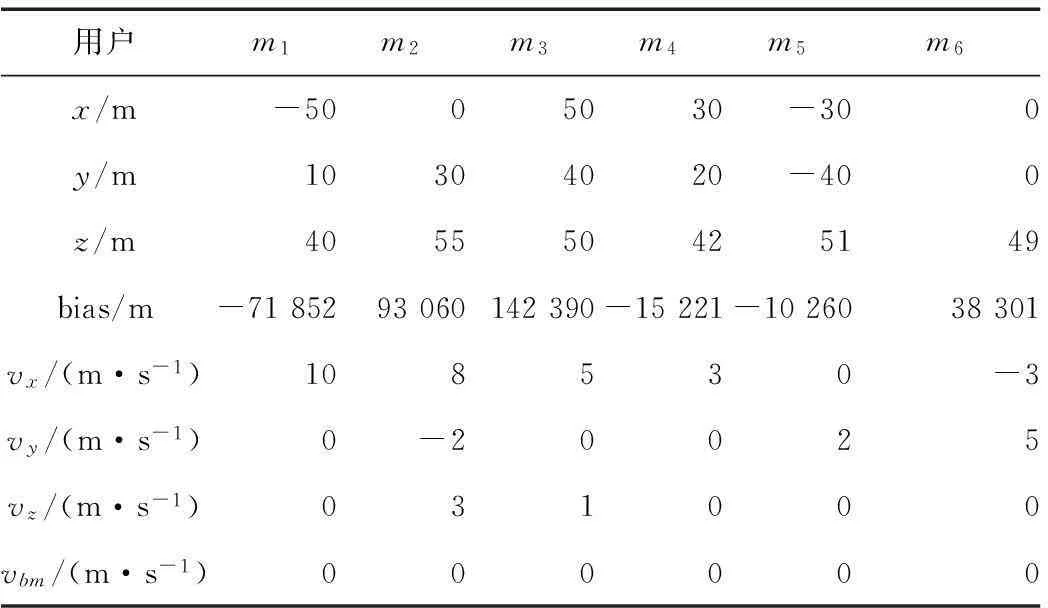
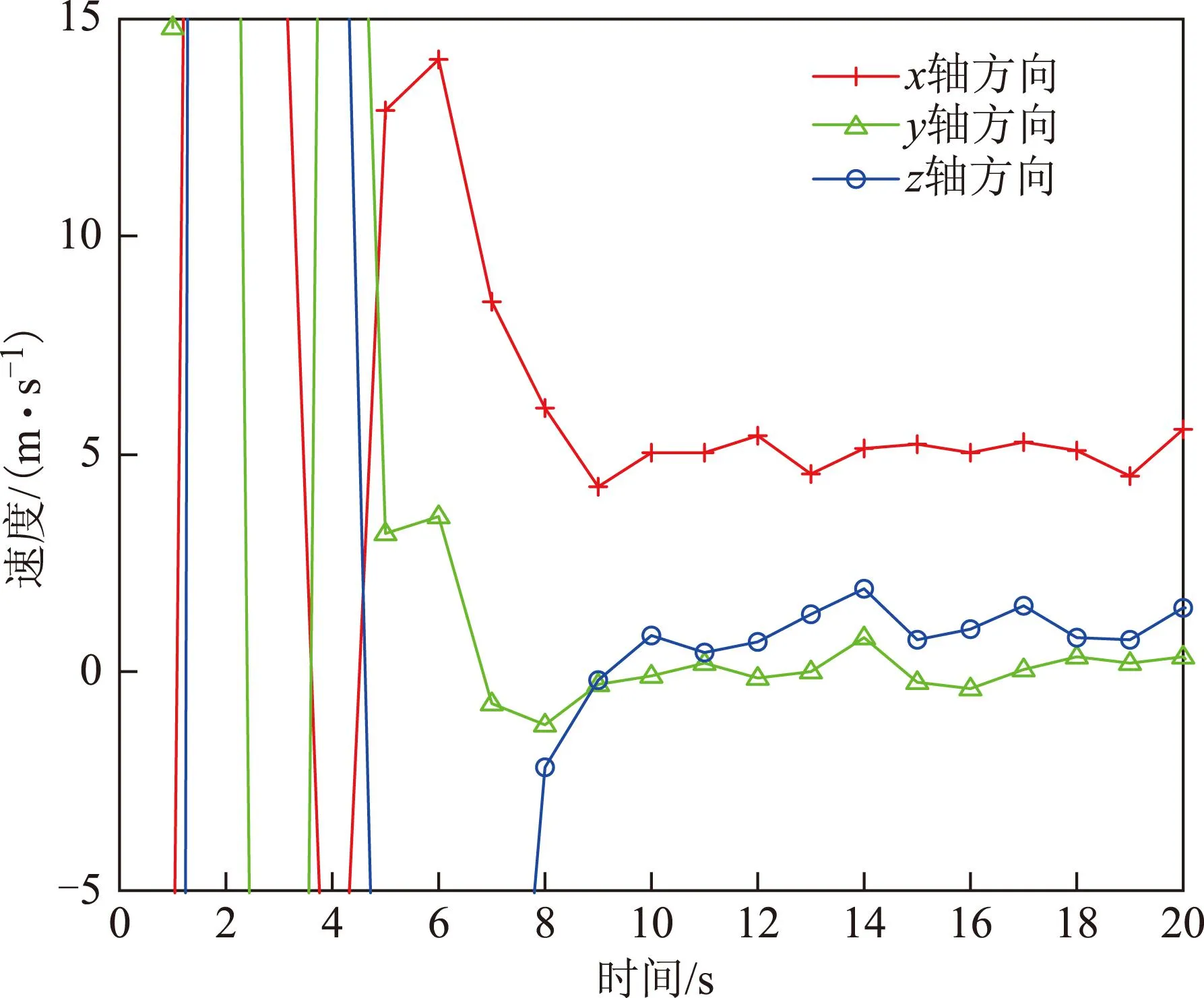
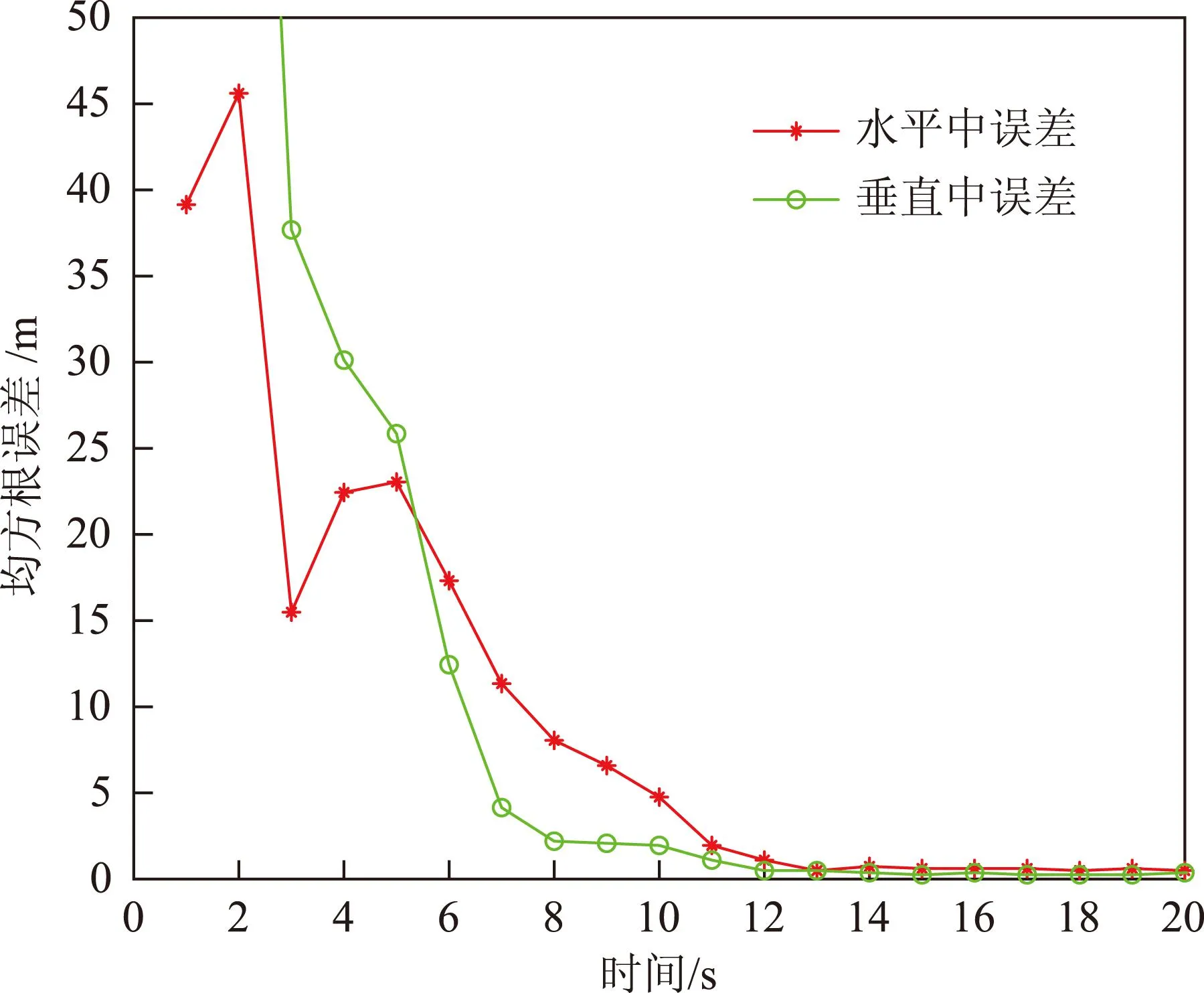
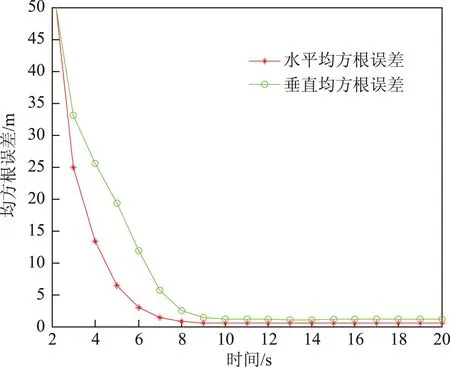
如果 在该时隙内迭代次数Niter 则将估计值作为预测值返回第3步 否则 进入第7步; 7:如果 估计总时间结束 则输出最终的估计状态值 否则 进入下一个时隙,返回第2步并将上一时隙 估计状态和协方差作为初始信息。 本文中用户之间的协同体现在彼此之间能相互测距并通过通信共享自己的位置信息。用户在更新自己的位置状态之前需要接收所有协同用户的估计位置信息,并向协同用户发播自己的位置信息。由于该网络为动态模型,为了更加准确快速的对状态进行跟踪估计,在每个更新间隔内还要进行n次迭代,这里取n=3。卫星的三维坐标通过STK软件实时产生。 4仿真验证与分析 本节给出了基于扩展卡尔曼的协同定位算法对图1所示场景的数值仿真结果。实验中,假设卫星在仿真的时间段内其位置信息是不变的,表2给出了卫星在地心地固坐标系(Earth-centered Earth-fixed,ECEF)中位置具体坐标*进行仿真的时候需要将其转换为站心坐标系坐标。表3给出了6个用户的初始状态,包括初始位置信息,钟差引起的伪距测量偏差和各个方向上的速度。 表3 各个用户的初始状态 图2 六个用户x轴方向的速度仿真曲 从图2可以看出,当估计时间在10 s之后,对其中各个用户的x方向上的速度估计比较精确,基本能够将误差收敛至2 m/s之内。对用户三x轴,y轴,z轴方向的速度估计如图3所示。从图3中可以看出,各个方向上速度估计的收敛速度相同,而且同一个点各方向上的方差大小也都基本相同,都在10 s以后能够将速度估计的误差收敛到2 m/s以内。 在对用户速度估计的同时,对用户的位置也进行估计,在20 s内,其水平和垂直方向上的中误差(root mean square error,RMSE)如图4所示。相对应的在静态模型中,水平和垂直方向上的中误差如图5所示。 图3 用户3速度估计 图4 动态模型中位置的RMSE 卫星编号S1S2S3S4S5S6S7x/m192635242612497624768710804802985438182082386-7307117y/m-13725770-57494201601307-130144371556101723437415-14002994z/m11583188-846377992557521563572196768441204814521528812 图5 静态模型中位置的RMSE 通过对比可以看出,动态模型中用户位置的中误差波动比较大,在10 s之后才能将水平中误差收敛到5 m以内。而在静态模型中,中误差分布比较平滑,在7 s以后,就能将水平中误差收敛到5 m。 5结束语 本文针对复杂环境下可见星不足导致的无法定位动态用户的问题,研究了基于协同定位的导航增强方法,通过扩展卡尔曼滤波实现了对动态用户的位置和速度的有效估计。从仿真结果可以看出,用户的速度估计在10 s以后,其方差可以控制在2 m/s以内,对其位置估计时,在10 s以后估计误差可收敛到5 m以内。同时,通过协同,原本可见卫星不足4颗的用户实现了定位,也即系统的可用性也得到了显著提高。然而还应该看到,与静态系统相比,动态系统内用户位置估计的方差会变大,位置收敛的速度也会变慢。这是在下一步的工作中需要解决的问题。 参考文献 [1]KURAZUME R,HIROSE S,NAGATA S,et al.Study on cooperative positioning system[EB/OL].(2015-03-21)[2015-06-18].http://www.researchgate.net/publication/3631511_Study_on_Cooperative_Positioning_System. [2]WYMEERSCH H,LIEN J,WIN M Z.Cooperative localization in wireless networks[J].Proceedings of the IEEE,2009,97(2):23-34.DOI:10.1109/JPROC.2008.2008853. [3]SHARP I,YU K G,HEDLEY M.On the GDOP and accuracy for indoor positioning[J].IEEE Transactions on Aerospace & Electronic Systems,2012,48(3):2032-2051. [4]CACERES M A,SOTTILE F,GARELLO R,et al.Hybrid GNSS-to a localization and tracking via cooperative unscented kalman filter[EB/OL].[2015-06-18].http://www.researchgate.net/publication/224205981_Hybrid_GNSS-ToA_localization_and_tracking_via_cooperative_unscented_Kalman_filter. [5]CACERES M A,PENNA F,WYMEERSCH H,et al.Hybrid GNSS-terrestrial cooperative positioning via distributed belief propagation[C]//The Institute of Electrical and Electronics Engineers(IEEE).Global Telecommunications Conference (GLOBECOM 2010).New York:IEEE,2010:1-5.DOI:10.1109/GLOCOM.2010.5683684. [6]SIMON D.Optimal state estimation:Kalman,H infinity,and nonlinear approaches[M].New Jersey:John Wiley & Sons,2006:88-89. [7]BELLANTONI J F,DODGE K W.A square root formulation of the Kalman-Schmidt filter[J].AIAA Journal,1967,5(7):1309-1314.DOI:10.2514/3.4189. [8]TIAN Shiwei,HUANG Boyu,LI Guangxia,et al.A perspective on Cramér-Rao bound for hybrid GNSS-terrestrial cooperative positioning[EB/OL].[2015-06-18].http://www.cnki.net/KCMS/detail/detail.aspx?QueryID=2&CurRec=1&recid=&filename=WXDH201405009017&dbname=CPFD0914&dbcode=CPFD&pr=&urlid=&yx=&uid=WEEvREcwSlJHSldSdnQ1V1lLcDUvRkY1aHhXeENsODZxK0Jsa1IyNTlTUjF6b1U3ZDJHUEpqMFl3UzZYOWZ2eVlB PT0=$9A4hF_YAuvQ5obgVAqNKPCYcEjKensW4IQMovwHtwkF4VYPoHbKxJw!!&v=MTg3NTZackc0SDlYT XFvOUZiZXNPQ3hOS3VoZGhuajk4VG5qcXF4ZEVlTU9VS3JpZlp1TnVGaXZrVXJmTElWd1dNalhQ. [9]PENNA F,CACERES M A,WYMEERSCH H.Cramér-Rao bound for hybrid GNSS-terrestrial cooperative positioning[J].IEEE Communications Letters,2010,14(11):1005-1007. A Research of Dynamic Cooperative Localization System via Extended Kalman Filter KEMingxing1,2,LÜJing1,2,TONGKaixiang1,2,ZHUMing1,2 (1.College of Communications Engineering,PLA University of Science and Technology, Nanjing 210007, China;2.Satellite Communication and Navigation Collaborative Innovative center Nanjing,210007, China) Abstract:The global navigation satellite system (GNSS) is widely used in navigation and positioning system.While in some GNSS-challenged environments,such as urban canyons,dense foliage and building block,it will fail to guarantee the service quality or can’t provide service at all.Several satellite enhanced means were presented to solve such problem and among them,the cooperative localization has great prospective as it can reduce the dependence of infrastructure.This paper established an equation of the system based on a position-velocity-time (PVT) model and employed the extended Kalman filter algorithm to estimate the user’s location and velocity in a dynamic cooperative localization system.This paper gave out the detailed derivation process and built the model though the three-dimension position of each satellite generated by software.The simulation results show that the algorithm can track the path of dynamic users and effectively estimate the user’s velocity. Key words:extended kalman filter;cooperative localization;dynamic system;performance estimation 中图分类号:P228 文献标识码:A 文章编号:2095-4999(2016)-01-0044-06 作者简介:第一柯明星(1990—),男,安徽安庆人,硕士生,主要从事卫星导航和室内外协同定位算法的研究。 收稿日期:2015-07-25 引文格式:柯明星,吕晶,童凯翔,等.基于扩展卡尔曼滤波的动态协同定位算法[J].导航定位学报,2016,4(1):44-49.(KE Mingxing,LÜ Jing,TONG Kaixiang,et al.A Research of Dynamic Cooperative Localization System via Extended Kalman Filter[J].Journal of Navigation and Positioning,2016,4(1):44-49.)DOI:10.16547/j.cnki.10-1096.20160109.