高超声速飞行器再入段滚转控制与舵系统技术指标

曹梦丹，王 勇，高亚楠

(北京控制工程研究所，北京100090)

高超声速飞行器再入段滚转控制与舵系统技术指标

曹梦丹，王 勇，高亚楠

(北京控制工程研究所，北京100090)

文章通过分析高超声速飞行器再入段横侧向对象特性，确定动压达到一定条件气动舵面完全参与姿态控制时的滚转控制策略.基于滚转回路结构，理论分析滚转回路性能指标与控制律参数的关系，估计舵系统带宽.结合仿真手段，给出典型状态下的定点计算结果，确定舵系统带宽要求.另外，通过仿真研究，探讨舵系统时间常数、阻尼比和时延对滚转控制品质的影响.

高超声速飞行器;滚转控制;舵系统带宽

0 引言

高超声速飞行器返回再入过程中，通过改变攻角和倾侧角控制飞行器的飞行轨迹，一般维持侧滑角在0°附近［1］.由于飞行器倾侧角不易测量，可以利用滚转角来近似代表飞行倾侧角.因此再入段横侧向姿态控制主要是飞行器滚转角控制.然而再入段大迎角、大马赫数飞行状态导致航向静不稳定、横航向强耦合、荷兰滚稳定性下降等问题，给横侧向的滚转轨迹跟踪带来很大困难［2］.

当动压达到一定条件，滚转姿态控制任务靠气动舵面完成［3］.舵系统作为控制系统的执行机构，其性能直接影响飞行器总体性能指标，决定着飞行的动态品质与姿态控制精度.文献［4］对某飞行器的舵回路建立了零位附近的小扰动线性化模型以及非线性模型，研究舵回路各种频域时域特性以及非线性、离散化对控制系统性能的影响.文献［5］从导弹自动驾驶仪设计角度出发，讨论舵机性能分析方法.文献［6］根据滚转回路特性，研究了舵机带宽相角对滚转回路性能的影响.文献［7］用连续二次规划方法来优化舵机性能，设计基于鲁棒思想的H∞控制器克服负载干扰对电动舵机的影响，以提高鲁棒控制性能.

本文针对飞行器不同阶段滚转控制策略，根据滚转设计指标要求确定控制参数，建立舵系统带宽与回路截止频率的关系，确定舵系统带宽指标.并探讨舵系统各项指标对滚转控制品质的影响.

1 滚转控制系统

1.1 基本特性

本文选用X-37B作为样例高超声速飞行器，气动布局采用翼身组合体，气动参考长度8.02 m，参考面积5.077 5 m2，结构质量2 700 kg.气动舵面包括V尾、副翼、体襟翼和阻力板，飞行器是左右面对称的.V尾反向偏转提供偏航力矩，起到方向舵作用，副翼反向偏转提供滚转力矩.本文重点研究方向舵和副翼的控制作用.

飞行器再入过程中，气动舵面和RCS(reaction control system)作为两套执行机构，执行机构的控制效率与动压直接相关.当动压达到一定条件时，气动舵面完全参与姿态控制，本文分析此工况飞行器再入段模态特性，以此确定滚转控制策略.

多输入多输出的线性系统可以描述为:

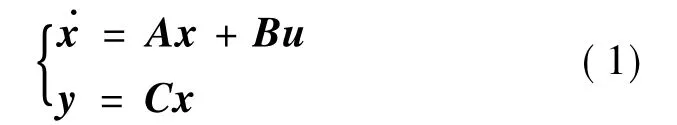
对于横侧向系统，式(1)中的状态变量x=［β p r］T分别表示侧滑角、滚转角、滚转角速率、偏航角速率，控制量u=［δaδr］T表示副翼和方向舵，输出量y=x，A为状态阵，B为控制阵.

飞行器的横侧向模态由荷兰滚模态、滚转模态和螺旋模态组成.滚转模态主要表现在扰动的初始阶段，对应横侧向特征方程的负实根.螺旋模态，对应特征方程的小实根，表现为偏航角和滚转角的单调和缓慢变化.荷兰滚模态是横侧向耦合产生的运动，表现为滚转角、偏航角和侧滑角随时间周期性变化，对应横侧向运动方程的一对共轭复根.如表1所示.整个再入过程滚转模态和螺旋模态的频率远低于荷兰滚模态，飞行器横侧向动态特性主要体现在荷兰滚模态上.

1.2 控制设计

滚转角速率到副翼的传递函数［2］如下:

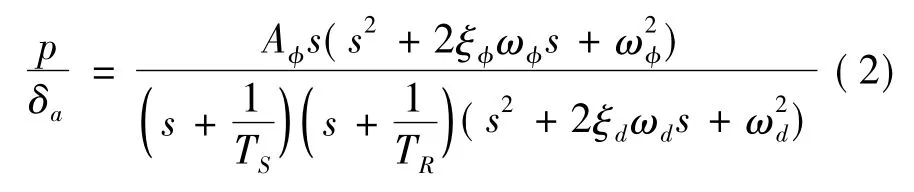
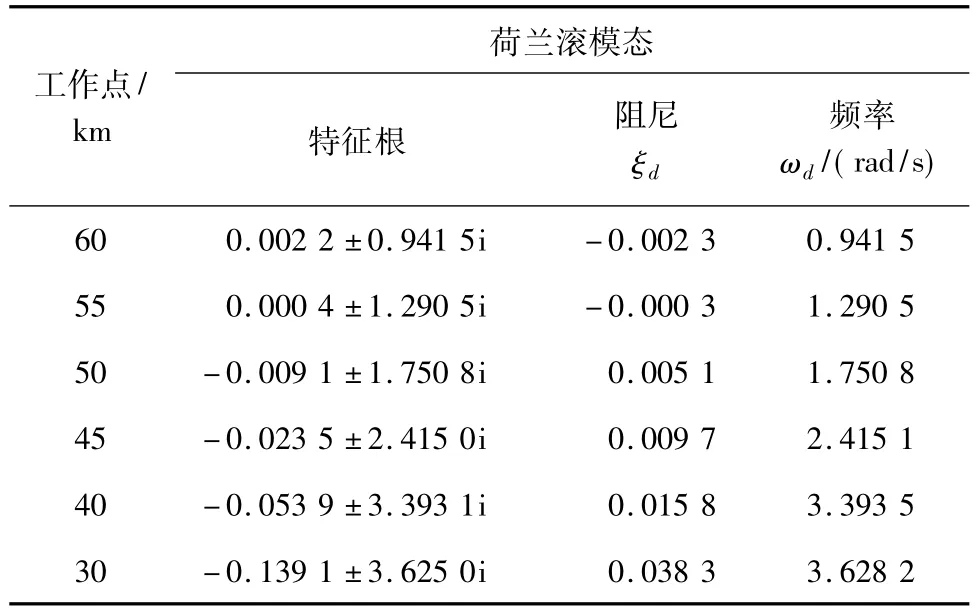
表1 荷兰滚模态分析Tab.1 The analysis of Dutch roll mode

式中，(ωd，ξd)是荷兰滚极点，TS、TR分别是螺旋模态和滚转模态的时间常数.滚转角速率反馈通道的有效性取决于开环二次零点(ω，ξ)的位置.

ω/ωd是副翼操纵能力的判据，用于考察滚转角速率到副翼的反馈，分析滚转角速率到副翼根轨迹的零极点分布:

1)ω/ωd≥1，飞行器进入末端能量管理段，迎角降低，航向静稳定性增大，ωφ更接近ωd，荷兰滚极点引出的根轨迹走向开环零点，滚转角速率反馈对荷兰滚的影响逐渐弱化，如图1(a)所示.

2)ω/ωd＜1，大马赫数飞行，航向静稳定性下降值小，使得ω值较小，而上反效应明显大负值，补偿了荷兰滚频率ωd，从荷兰滚极点引出的根轨迹落到实轴上，增大通道增益能明显增大荷兰滚阻尼，如图1(b)所示.

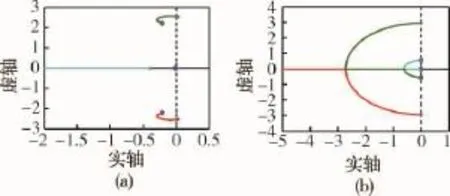
图1 滚转角速率到副翼舵反馈根轨迹示意图Fig.1 Root locus plot of roll rate to aileron

偏航角速率到方向舵的传递函数如下［2］:

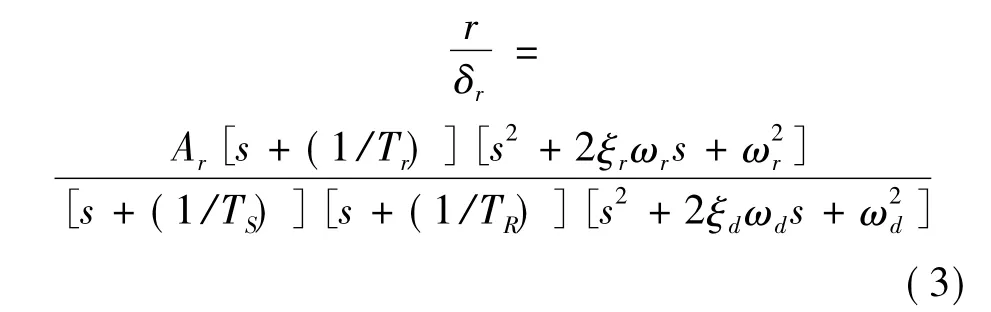
偏航角速率反馈通道的有效性取决于开环二次零点(ωr，ξr)的位置，ωr/ωd是方向舵操纵能力的判据，分析偏航角速率到方向舵根轨迹零极点分布:

1)ωr/ωd＜1，此时增大通道增益能明显增大荷兰滚阻尼，如图2(a)所示;

2)ωr/ωd≥1，随着迎角和马赫数增大，偏航角速率反馈不能改善荷兰滚阻尼，1/Tr处于1/TR左侧，由滚转模态和螺旋模态引出的根轨迹往左移动，增大通道增益将增大滚转模态频率，如图2(b)所示.

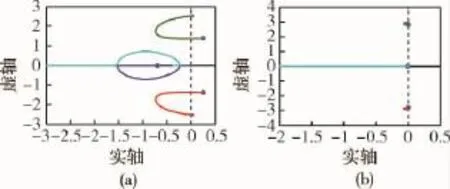
图2 偏航角速率到方向舵反馈根轨迹示意图Fig.2 Root locus of yaw rate to rudder

因此，初期再入段与常规的控制策略相反:用滚转角速率到副翼的反馈改善荷兰滚模态，而依靠偏航角速率到方向舵的反馈改善滚转模态.末端能量管理段，迎角降低，横侧向采用常规控制方案，方向舵增稳荷兰滚，副翼控制滚转.结合增稳回路和滚转回路，再入阶段的控制律为

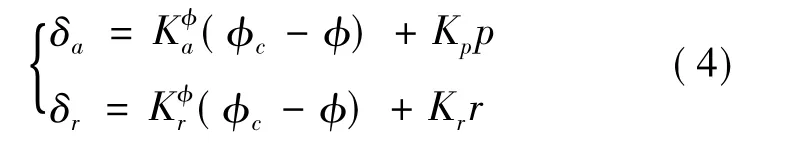
考虑两种控制方案间的切换，通过增益调度就可以实现.方向舵控制滚转能力弱化和副翼控制滚转能力的改善是个平滑变化的过程，控制切换并不要求明确的切换时机.如再入段初期，副翼仅有阻尼回路，设置=0;随着高度降低，进入末端能量管理段初期还继续使用方向舵控制滚转，当马赫数小于3，切换成副翼控制滚转，增益=0.根据马赫数进行切换，为避免振荡，切换过程进行副翼和方向舵的速率软化［2］.

2 舵系统技术指标

2.1 舵系统模型

舵系统的数学模型采用带延迟的二阶环节描述:

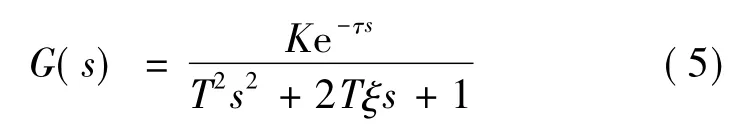
式中:K为比例因子，表征了舵系统输入输出稳态比例关系，这里进行归一化处理;T=1/ωn;T为时间常数;ωn为自然频率;ξ为阻尼比;e－τs反映舵系统时延效应.

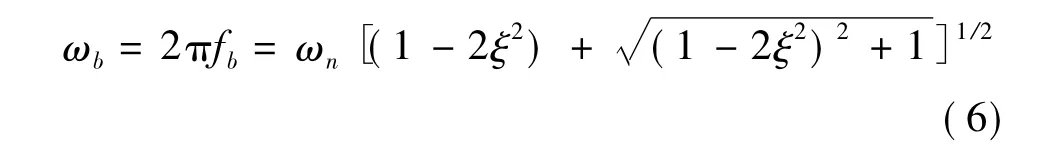
式中，fb为舵系统频带宽度，体现自然频率和阻尼比两项指标.

2.2 舵系统带宽

在舵系统设计时，通常由通频带来描述其其动态品质.舵系统的频带越宽，越能正确反应变化速度较快的控制指令.根据两种滚转控制策略来确定舵系统带宽要求.

2.2.1 方向舵控制滚转

根据控制策略的分析，初期再入段采用非常规控制策略:滚转角速率到副翼的反馈增稳荷兰滚.而对于滚转控制回路，采用偏航角速率的反馈改善滚转模态频率特性，反馈滚转角的偏差实现对滚转角的控制.如图3所示(舵系统忽略时延影响).

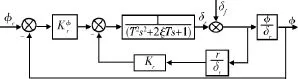
图3 滚转回路传递函数结构图(方向舵)Fig.3 Block diagram of transform function for roll loop by rudder

对于角速率反馈回路，舵系统作为二阶环节，相当于开环增加两个极点，且T越小，舵系统形成的开环极点相对于偏航角速率反馈开环零极点离虚轴越远，对角速率运动极点形成的根轨迹影响越小，如图4所示.

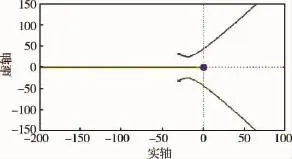
图4 角速率反馈开环根轨迹图Fig.4 Root locus of angular rate feedback

滚转角到方向舵的传递函数为

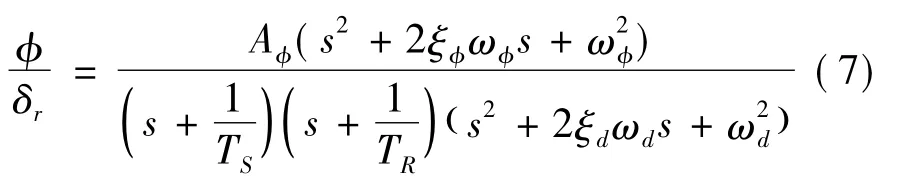
一般情况舵系统高频响应特性不影响系统主导极点，即不影响系统稳定性，忽略舵系统，滚转通道闭环传递函数为

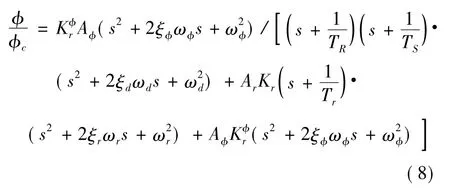
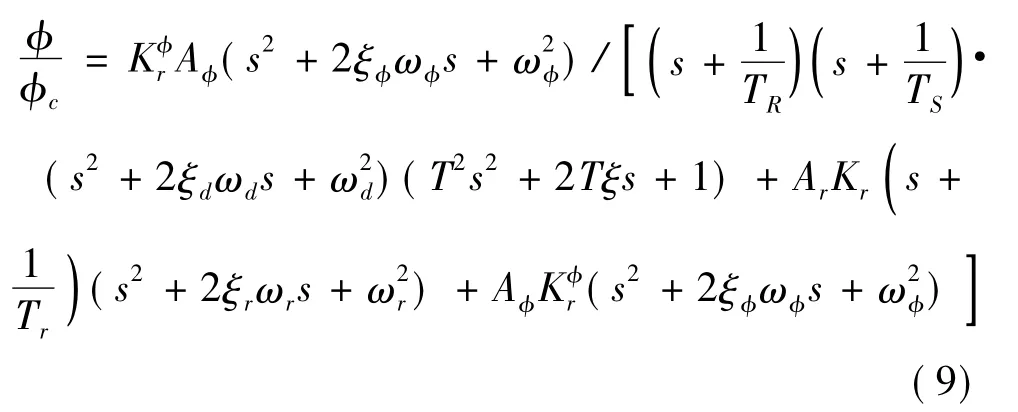
带舵环节后，滚转回路变为六阶系统，原四阶系统的频率响应被改变，通道带宽也被拓宽.

2.2.2 副翼控制滚转

根据控制策略的分析，末端能量管理段采用常规控制策略:偏航角速率到方向舵的反馈增稳荷兰滚.对于滚转控制回路，采用滚转角速率的反馈改善滚转控制回路的阻尼特性，反馈滚转角的偏差实现对滚转运动特性的改善，同时达到抑制螺旋运动的目的，如图5所示.

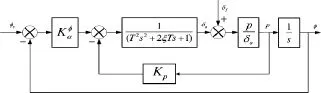
图5 滚转回路传递函数结构图(副翼)Fig.5 Block diagram of transform function for roll loop by aileron

此时迎角降低，航向静稳定性增大，ω更接近ωd，滚转运动的二次零点和荷兰滚极点形成偶极子，相互抵消，滚转角速率到副翼舵的传递函数为

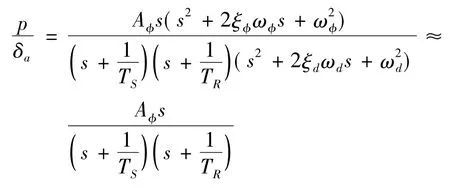
由传递函数结构图得到滚转干扰等效舵偏到滚转角的传递函数为

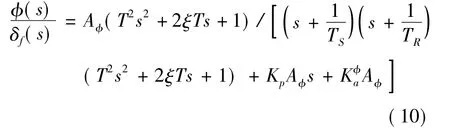
当干扰等效舵偏为阶跃作用时，

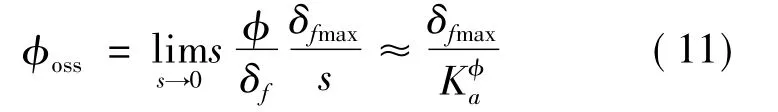
由于舵系统相对飞行器环节动态特性较快，滚转回路可先忽略其动态特性的影响，用二阶传递函数进行，则滚转回路的闭环传递函数为

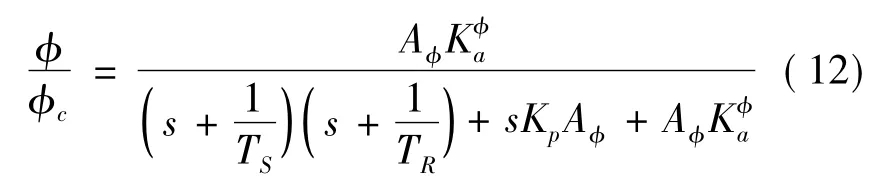
将其转化为标准形式

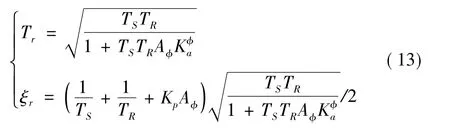
由闭环传递函数频率特性求得带宽表达式

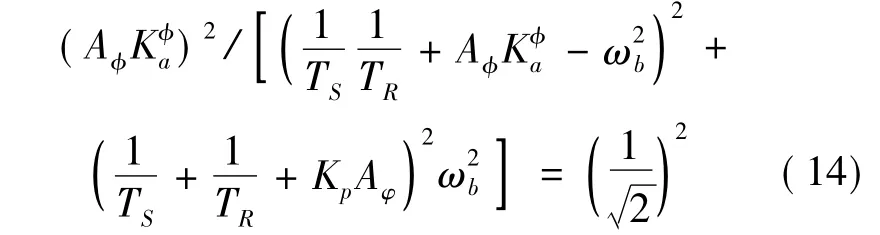
由开环传递函数式得到截止频率表达式

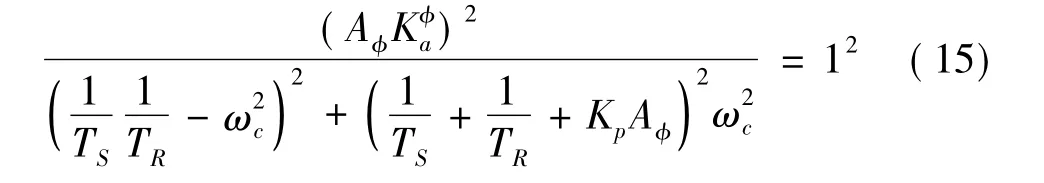
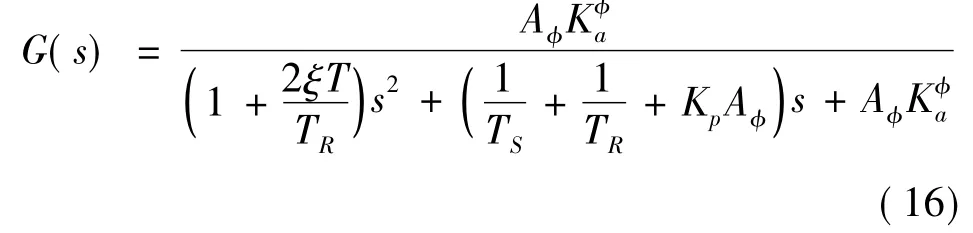
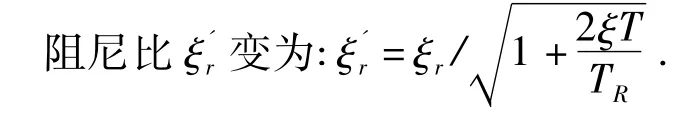
3 仿真分析

3.1 舵系统带宽的确定

某高超声速飞行器滚转回路设计要求为:A.稳定性要求:相角稳定裕度不小于45°，幅值稳定裕度不小于8 dB;B.快速性要求:超调小于5%，调节时间小于10 s;C.滚转角误差:飞行滚转角γ＜2°.

根据设计要求，选取不同特征点进行分析，控制律增益和舵系统带宽要求如表2所示.

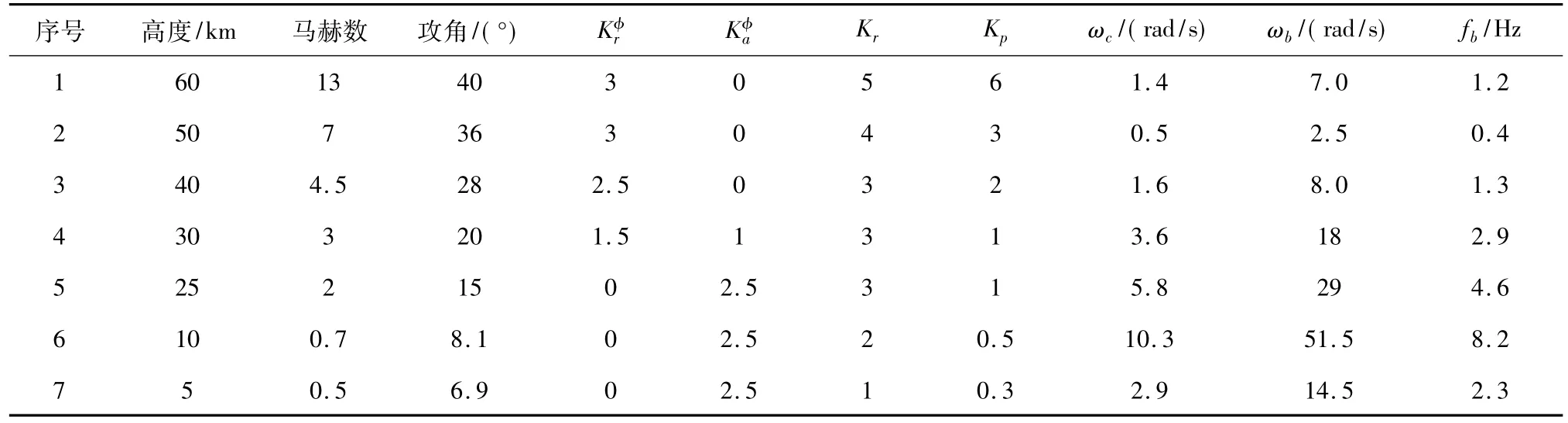
表2 特征点控制律增益与舵系统带宽Tab.2 Control parameters and rudder bandwidth in the different flight feature points

综合以上，要满足滚转回路设计要求，且保证一定裕量，舵系统带宽应不小于10 Hz.

3.2 舵系统不同参数的影响

3.2.1 时间常数

取再入段某一特征点，分析比较舵系统带宽分别为12 Hz(T=0.013 4 s)和16 Hz(T=0.010 1 s)，阻尼比为ξ=0.7滚转回路性能.

图6(a)所示为不同时间常数下滚转角响应，(b)为其响应过程中的放大图，表3所示为滚转控制时域频域品质，可见T越小，调节时间减小，超调减小，幅值稳定裕度和相角稳定裕度都有所增大，滚转回路时域频域品质变好.

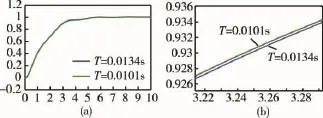
图6 不同时间常数下滚转角响应Fig.6 Roll angle responses in different time constants

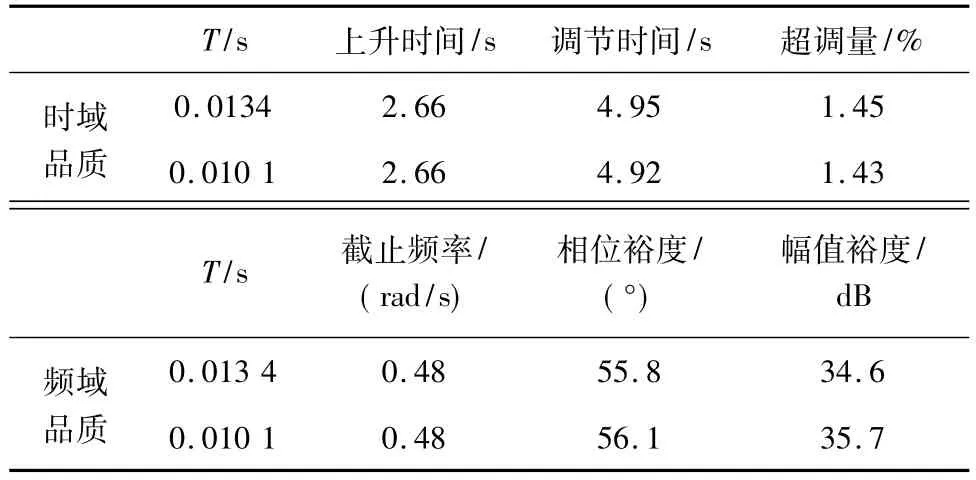
表3 不同时间常数下滚转控制时域频域品质Tab 3 The qualities of roll control time and frequency domain in different time constants

3.2.2 阻尼比

舵系统在自然频率一定时，其阻尼比对滚转控制回路的影响十分有限.在满足舵系统带宽最小要求时，阻尼比对于时频域品质的影响不敏感

3.2.3 时延

舵系统时延一般由舵系统固有属性引起.

图7(a)所示为时延τ=0、τ=0.1、τ=0.2和τ=0.3的阶跃响应曲线，表4所示为时延τ=0、τ= 0.1和τ=0.2滚转控制时域频域品质，可见随时延增大，动态响应变慢，时域频域品质均变差.图7(b)所示为τ=0.21、τ=0.24、τ=0.27和τ=0.3的阶跃响应曲线，随时延逐渐增大，回路稳定性降低，振荡越来越大，迟延为0.27 s时回路仍可在10 s内达到稳态，当迟延增大到0.3 s时，振荡明显增大，系统不稳定，因此应尽量控制时延在0.3 s以内.

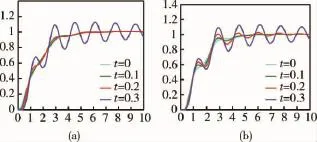
图7 不同时延下滚转角响应Fig.7 Roll angle responses in different delay time

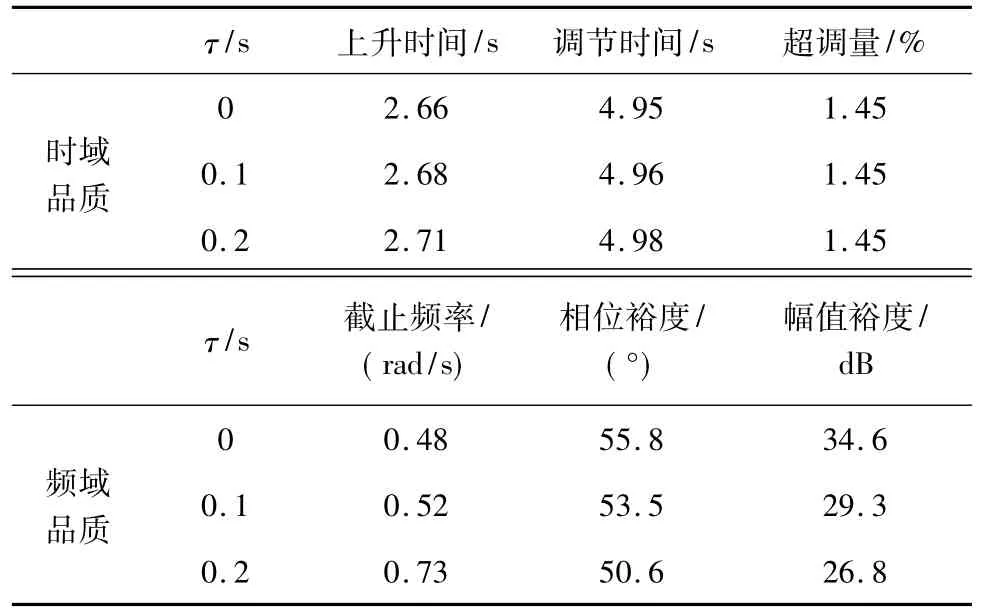
表4 不同时延下滚转控制时域频域品质Tab 4 The qualities of roll control time and frequency domain in different delay time

4 结论

高超声速飞行器滚转控制与舵系统性能密切相关.本文针对再入段特性，采用初期再入段通过方向舵、末端能量管理段通过副翼控制滚转的控制策略，并通过解析和仿真结合的方法设计控制参数，确定舵系统带宽.研究表明，针对某高超声速飞行器，舵系统带宽至少达到10 Hz可以满足滚转稳定控制指标要求.根据仿真结果，在满足舵系统带宽基础上，舵系统时间常数越小，滚转控制性能越好;阻尼比对滚转控制品质影响不大;时延越大，系统性能越差，且舵系统时延应控制在一定范围.

［1］BENNETT D E.Space shuttle entry flight control overview［J］.Journal of Astronautics Science FEB，1983: 568-578.

［2］吴了泥.可重复使用运载器亚轨道再入段制导与控制技术研究［D］.南京:南京航空航天大学，2009.

WU L N.Research on guidance and control technology of suborbital reentry for reusable launch vehicle［D］.Nanjing.Nanjing University of Aeronautics and Astronautics，2009.

［3］JUNG D W，LOWENBERG M H，JONES C D C.Integration of control allocation methods in bifurcation analysis framework［C］//AIAA Guidance，Navigation and Control Conf.and Exhibit’.Washiton D.C.:AIAA，2006.

［4］王纪森，钟丹华.飞行器舵回路仿真研究及试验分析［J］.机床与液压，2006(9):134-136.

WANG J S，ZHONG D H.Research on model and simulation of an aerocraft rudder loop［J］.Machine Tool＆Hydraulics，2006(9):134-136.

［5］杨育荣，王建琦，李友年.空空导弹舵机性能分析方法［J］.弹箭与制导学报，2012，32(5):57-60.

YANG Y R，WANG J Q，LI Y N.Performance analysis method of air-to-air missile actuator［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2012，32 (5):57-60.

［6］张跃，段镇.轴对称飞行器滚转稳定控制与舵机技术指标［J］.光学精密工程，2010，18(1):100-107.

ZHANG Y，DUAN Z.Roll stable control and rudder’s technologic parameters of axisymmetric aircrafts［J］.Optics and Precision Engineering，2010，18(1):100-107.

［7］LU H，LI Y，ZHU C.Robust synthesized control of electromechanical actuator for thrust vector system in spacecraft［J］.Computers＆Mathematics with Applications，2012，64(5):699-708.

Roll Control and Rudder System’s Technologic Parameters of Hypersonic Vehicle in Reentry Phase

CAO Mengdan，WANG Yong，GAO Yanan
(Beijing Institute of Control Engineering，Beijing 100090，China)

The design of roll control is presented under the certain dynamic pressure condition that aerodynamic rudder is completely used for attitude control，via the analysis of stability and control characteristic on reentry of hypersonic vehicle.According to the roll-loop structure，the relationship between rollloop performance index and control parameters is analyzed，and the rudder bandwidth is estimated.On this basis，the minimum rudder bandwidth in different flight feature points is given.In addition，with the help of the simulation results，the effects of time constants，damping ratio and delay time of the rudder system on the performance of roll control quality are studied.

hypersonic vehicle;roll control;bandwidth of rudder system

V414

A

1674-1579(2016)04-0018-06

10.3969/j.issn.1674-1579.2016.04.004

曹梦丹(1990—)，女，硕士研究生，研究方向为导航、制导与控制;王 勇(1972—)，男，研究员，研究方向为导航、制导与控制;高亚楠(1977—)，男，研究员，研究方向为导航、制导与控制.

2016-04-18