基于分层随机梯度辨识算法的传感器故障检测方法*

符方舟，王大轶，2，李文博，2

(1.北京控制工程研究所，北京100090;2.空间智能控制技术重点实验室，北京100190)

基于分层随机梯度辨识算法的传感器故障检测方法*

符方舟1，王大轶1，2，李文博1，2

(1.北京控制工程研究所，北京100090;2.空间智能控制技术重点实验室，北京100190)

提出一种基于两阶段递推随机梯度参数辨识的传感器故障的在线检测方法.相对于最小二乘参数辨识算法，随机梯度参数辨识算法所需计算量更小.针对计算能力受限的系统，提出基于随机梯度参数辨识的检测算法.通过分析可知，参数辨识精度越高时检测精度越高.为提高精度，给出基于两阶段递推随机梯度参数辨识的检测算法并设计基于最新估计信息的残差.除此之外，还给出新的检测算法与原有的基于最小二乘检测算法计算量的对比分析，并通过仿真实例，证明新的检测算法的优越性及有效性.

分层随机梯度;传感器故障;故障检测

0 引言

随着科学技术的飞速发展，实际工程的投资规模以及系统的复杂程度也日益提高.保障控制系统的可靠性和安全性具有非常重要的意义.传感器作为控制系统的重要组成部分，人们对其可靠性提出了越来越高的要求.

近二十年以来，越来越多的学者对故障诊断分析方法进行研究，通常可划分为3类［1］:基于信号处理、解析模型和基于知识的方法.其中，基于解析模型的故障检测与诊断方法有着最广泛的应用［2-4］.系统参数估计是基于解析模型故障诊断的一种重要方法.文献［5］在闭环的条件下研究了一种辨识条件不充分的多输入多输出系统.先构造出降维模型并辨识相应的特征参数，通过特征参数的在线辨识结果检测系统因故障导致的参数变化.文献［6］中通过对递归最小二乘法对柴油发动机的废气再循环系统进行故障诊断，并通过改进递归总体最小二乘法减小参数不确定性以及传感器噪声，提高了系统的诊断精度.然而，现有的基于系统参数估计的故障诊断也存在一定的问题:在很多实际系统中，由于性能的限制，最小二乘算法极大的计算量会给系统造成极大的负担，这使得在线诊断无法实现.相对于最小二乘参数辨识，随机梯度参数辨识作为另一种经典辨识算法，具有计算量小的优点.近年来，许多学者对随机梯度辨识算法进行了深入研究，取得了丰硕成果［7-8］.文献［9］中对可变桨距的风力涡轮机故障诊断方法进行研究，利用基于多新息遗忘因子的随机梯度参数辨识方法，将故障诊断问题转换为参数辨识的问题，并通过调节新息长度达到提高辨识精度的效果.然而该文献仅针对系统的参数故障，未考虑传感器故障的情况.

鉴于上述基于参数辨识故障检测的工程意义和现有方法的不足，本文针对白噪声下的一般离散线性随机系统模型，提出了基于两阶段递推随机梯度辨识算法的故障检测方法.首先，直接采用随机梯度参数辨识算法通过求取系统残差，检测系统故障;然后，通过分析辨识精度与故障检测精度之间内在联系，证实了系统辨识精度对不同种类故障检测结果具有不同的影响;进而，以此分析结果对所提出的故障检测算法进行改进，增加检测精度;最后，对所提出的算法的计算量进行分析，并分别以传感器恒增益故障、恒偏差故障、卡死故障和软故障等情况对算法进行仿真验证，证实了该检测算法的优越性与有效性.

1 问题提出

对于一般的控制系统，其动态特性复杂且存在噪声、干扰等作用，故考虑如下离散线性系统的输入输出方程其中，t表示离散后的迭代步数，{u(t)}和{y(t)}分别是系统的输入序列和输出序列，v(t)是零均值的白噪声.z－1是单位后移因子.A(z)和B(z)是具有后移因子的多项式，并有如下形式:

其中na和nb是已知的.

定义其系数θ和信息量φ(t)为

由式(1)～(3)可知

对于系统(4)，选取误差准则函数

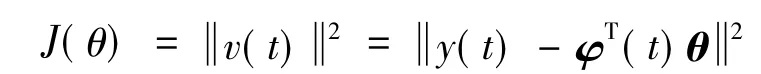
通过梯度搜索原理极小化误差准则函数，可以得到系统(4)的随机梯度算法［7］

通过对系统进行实时辨识，得到每一时刻t的系统残差

显然，当系统正常时，其残差re(t)近似为均值为0的高斯白噪声.当系统处于异常状态时(发生故障)，其残差re(t)会有明显的变化.因此，我们可以根据残差的变化对系统进行故障检测.为了提高故障检测精度，接下来对影响精度的因素进行分析.

2 影响检测精度的因素

显然地，阈值的选取直接影响检测精度，这在下节会详细分析.除此之外，我们通过分别考虑传感器的不同故障，研究影响检测精度的其余因素.

从式(8)可以看出，t时刻的残差主要由φT(t)θ、ε(t)和v(t)决定，其中(α－1)φT(t)θ直接反映发生故障时系统输出相对正常系统输出的偏移程度，显然|α－1|越大故障越容易被检测.而φT(t)ε(t)和v(t)相当于残差的“误差项”，两者直接关系着故障检测的精度.显然，噪声v越小时检测精度越高.在α保持不变的情况下，输出向量与实际参数向量的乘积φT(t)θ越大，越能反映故障系统的偏移程度，此时噪声v对残差的影响减小，故障检测的精度提高.其次，当算法参数辨识精度较高时，其残差可近似为r(t)≈(α－1)φT(t)θ+v(t)，即检测精度与系统的故障检测精度成正比.

(2)考虑传感器恒偏差故障

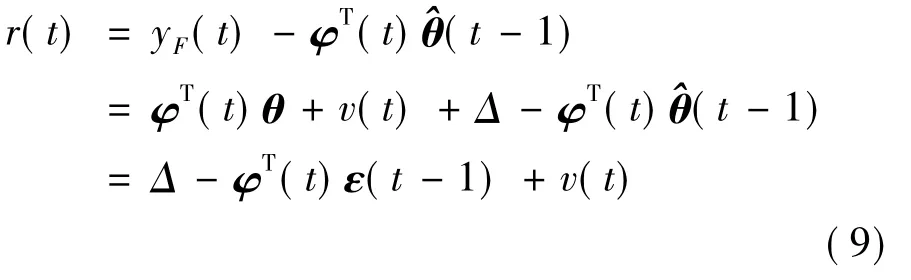
同理，从式(9)可知，t时刻的残差主要由φT(t)ε(t)、Δ和v(t)决定，其中Δ为发生故障时系统输出相对正常系统输出的偏差程度.φT(t)ε(t)和v(t)直接影响故障检测的精度.显然，噪声v越小时检测精度越高.同样的，当算法参数辨识精度较高时，其残差可近似为e(t)≈Δ+v(t)，也可增加系统的故障检测精度.

(3)考虑传感器卡死故障

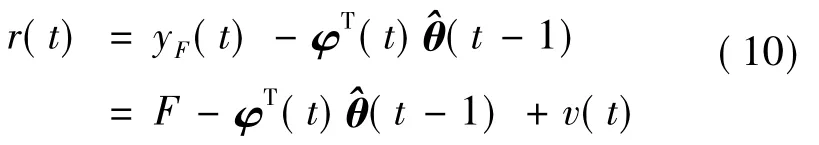
对于式(10)，辨识算法的精度对t时刻的残差r(t)无影响，只由上一时刻的估计状态的具体值φT(t)(t－1)和v(t)决定.当|F－φT(t)(t－1)|越大，发生故障时残差的突变就越明显.同样的.噪声v越小时检测精度越高.

(4)最后考虑传感器的软故障的情况.由式(11)可知，与偏差故障类似，较小的噪声v以及较高的算法参数辨识精度都能提高故障检测精度.

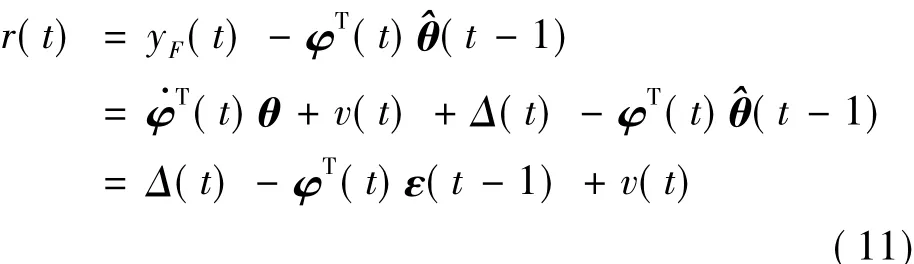
综上所述，对于大部分传感器故障，提高辨识算法的精度均有助于提高辨识的精度.相对于最小二乘算法，随机梯度算法具有计算量小的优点［10］，然而由于其收敛速度较慢以及精度较低，直接运用于系统的故障检测会影响检测精度.因此，为了提高其精度，接下来使用两阶段递推优化的方法对随机梯度算法进行优化.

3 基于分层递推随机梯度算法的故障检测

首先，将系数矩阵和信息向量分层，有

其中na+nb=n.由(12)－(15)，系统(4)可改写为

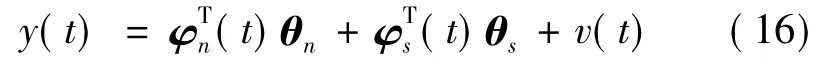
对于系统(16)，选取如下中间变量

则系统(16)可以分解成两个中间的子系统

其中y1(t)，φn(t)和θn分别为子系统(17)的输出向量、信息向量和参数向量;y2(t)、φs(t)和θs分别为子系统(18)的输出向量、信息向量和参数向量.参照随机梯度算法的推导步骤，分别对子系统进行分析，得到系统(4)两阶段递推随机梯度辩识算法为

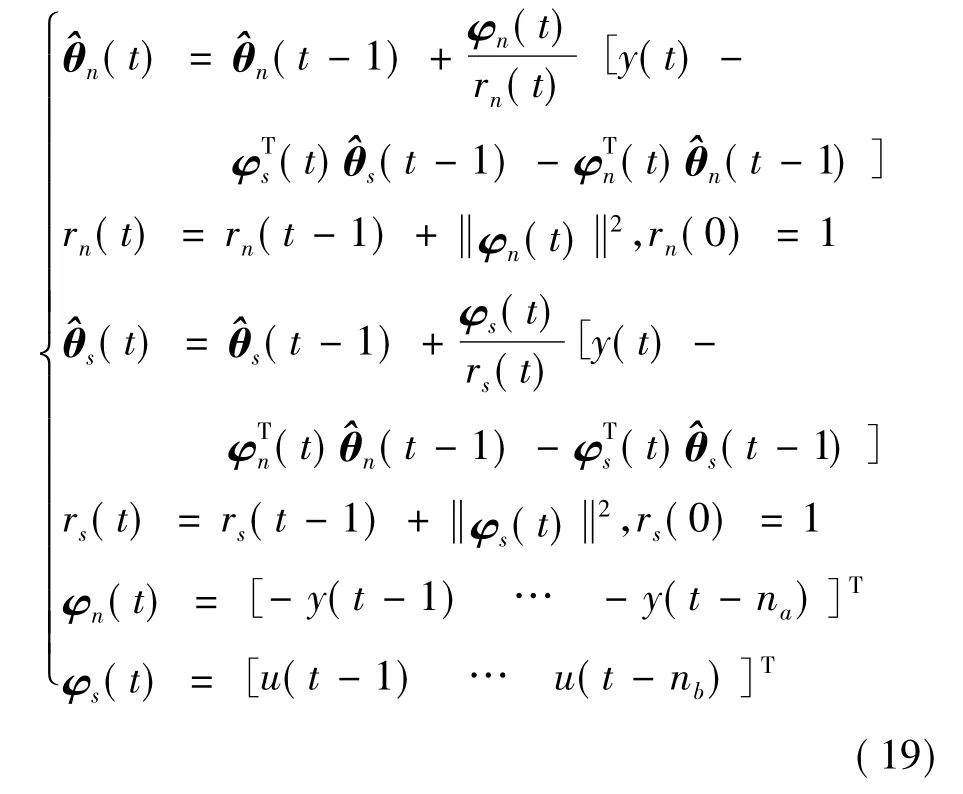
如上节所示，通过对系统进行实时辨识，得到每一时刻t的系统的残差

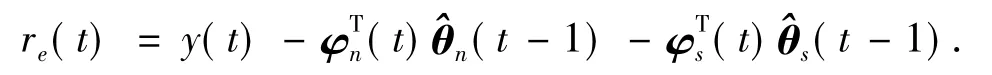
显然，当系统正常时，其残差re(t)近似为均值为0的高斯白噪声.当系统处于异常状态时(发生故障)，其残差re(t)会有明显的变化.因此，可以根据残差的变化对系统进行故障检测.

值得注意的是，在t时刻θn与θs的估计值n(t)与s(t)已经被估计出来，而此时计算残差re(t)用的依旧是θn和θs在上一时刻的估计值n(t－1)和s(t－1).不失一般性，随着算法的递推执行，系统的参数估计越来越接近于其真值.因此用n(t)与s(t)分别代替残差re(t)中的参数估计n(t－1)和s(t－1)可以进一步提高故障检测的精度.基于此，给出基于最新估计信息的残差表达式

实质上，所提出的残差式(20)相当于将式(8)、(9)和(11)中，t－1时刻的参数估计误差ε(t－1)替换为最新时刻的参数估计误差ε(t)，显然，在状态估计的过程中参数估计误差会随着时间逐渐降低，因此新残差式能有效增加检测精度.

为了减小噪声对检测结果的影响，进一步提高检测精度.在使用残差进行故障检测前，我们采用加权平方和对残差进行处理.因此，在使用残差进行故障检测前，采用加权平方和对残差进行处理

其中，N为数据窗口长度，当N取较大时，能提高检测系统的鲁棒性并降低故障的误报率，但同时会增加检测系统的计算负担，故在选择数据窗口长度时，应均衡考虑故障的准确率与计算量.

设定检测阈值为H，当S(k)在k时刻超出阈值H，即S(k)＞H，则称系统在k时刻发生故障.反之，若S(k)在k时刻小于阈值H，即S(k)＜H，则称系统此时为正常的.选取检测阈值需要充分考虑检测系统的误报率与检测精度.当阈值较大时可以很好地抑制检测系统的误报，然而却降低了检测系统的精度;相应的，当阈值较小时，会大大增加系统虚警概率.在本文中，假设已知系统从t1到t2时刻之间是无故障的，则选取检测阈值，k=t1， t1+1，…，t2，其中β为放大系数，用于调整误报率与检测精度之间的关系.

至此，给出了基于两阶段递推随机梯度参数辨识的检测算法，接下来将通过对比两阶段递推随机梯度参数辨识检测算法与递推最小二乘参数辨识检测算法的计算量，验证所提出的检测算法的优势.

4 计算量对比

通常用算法的乘法次数和加法次数来衡量算法的计算量.将一次加法运算和一次乘法运算统称为一个flop，即一次浮点运算.乘法运算次数和加法运算次数之和的flop数作为算法的计算量［11］.

由于检测算法在处理残差的部分计算量相同，这里就仅对两种参数辨识算法的计算量进行对比.递推最小二乘算法的表达式如下［12］:

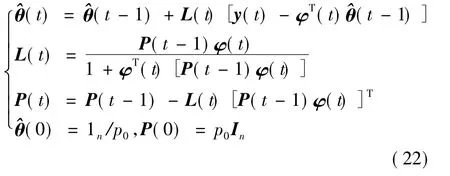
通过计算，可以得出递推最小二乘算法的计算量如表1所示.其中，n表示系统待辨识参数的个数.同理，由式(19)可得两阶段递推随机梯度参数辨识检测算法的计算量如表2所示.

表1 递推最小二乘参数辨识算法的计算量Tab.1 Flop count of recursive-least-squares identification algorithms

表2 两阶段递推随机梯度参数辨识检测算法的计算量Tab.2 Flop count of hierarchical stochastic gradient identification algorithms

通过上述分析可以发现，相对于递推最小二乘参数辨识算法，两阶段递推随机梯度参数辨识检测算法所需的计算量对n的增加不敏感.相对于已有的检测算法，所提出的检测算法具有更高的计算效率.接下来，将通过仿真算分析其有效性.

5 仿真算例与分析

考虑如下传感器系统

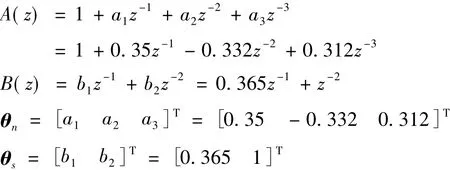
由于系统在实际运行的过程中系统的输入和输出不可避免地会受到噪声及扰动的影响［10］，因此带有白噪声的系统输入输出方程为

其中:输入u(t)=10sin(0.01t)+w(t)，10sin(0.01t)为系统的控制输入;w(t)为均值为零，方差=1的外部扰动;{w(t)}为均值为零，方差=0.52的白噪声序列.采样间隔为0.05 s.选取检测阈值.3S(k)，k=500，501，…，1 000.考虑如下故障:

(1)t=1 500步时，发生恒增益故障，y(t)= αytrue(t)，其中ytrue(t)为标称输出，下文表示方法相同，且增益系数α=1.2，结果如图1所示.

图1 恒增益故障的仿真曲线Fig.1 Residual with a constant gain fault

由图1可知，注入恒增益故障后，检测系统能及时且准确地反映出故障情况.

(2)t=1 500步时，发生恒偏差故障，有y(t)= ytrue(t)+Δ，偏差Δ=0.7，结果如图2所示.

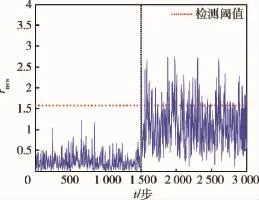
图2 恒偏差故障的仿真曲线Fig.2 Residual with a constant bias fault

从图2可以看出，当系统发生恒偏差故障时，所得到的基于最新估计信息的残差超过了所设定的阈值，有效地检测出系统的故障.

(3)t=1 500步时，发生卡死故障，此时有y(t)=F，其固定值F=0，结果如图3所示.

图3 卡死故障的仿真曲线Fig.3 Residual with a blocking fault

图3表示的是系统发生卡死故障的仿真曲线.显然地，本文提出的基于两阶段随机梯度检测算法可以有效地检测系统该类故障类型.

(4)t=1 500步时，发生软故障，此时有y(t)= ytrue(t)+Δ(t)，其中Δ(t)=0.000 3 t，结果如图4所示.

由图4可知，在系统在运行一段时间后，出现性能的退化，即发生软故障，检测系统能在故障发生后一段时间内检测到该类故障.其检测时延主要是由偏差的斜率所决定的，当偏差斜率较小时，由于故障初期对系统的影响较小，不能明显地由残差反应.直到故障积累到足够大的程度，导致残差超过所设定的阈值，检测系统才能检测出该故障.

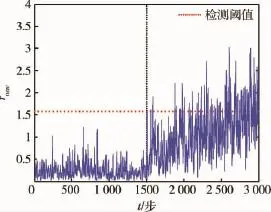
图4 软故障的仿真曲线Fig.4 Residual with a soft fault

6 结论

针对基于参数估计的故障检测方法进行深入研究，本文提出了一种基于两阶段随机梯度辩识的故障检测方法.通过理论推导和仿真分析可知，在保证一定精度的条件下，相对于已有基于最小二乘参数估计的故障检测方法，该检测方法具有计算量小的优点，可提方法可实现计算能力受限的控制系统传感器故障的在线检测.扩大已有的参数估计的故障检测方法的适用范围.

［1］周东华，王桂增.第五讲故障诊断技术综述［J］.化工自动化及仪表，1998，25(1):58-62.

ZHOU D H，WANG G Z.Chapter 5 review of fault diagnosis technology［J］.Control and Instrument in Chemical Industry.1998，25(1):58-62.

［2］WANG Y，ZHENG Y，FANG H，et al.ARMAX model based run-to-run fault diagnosis approach for batch manufacturing process with metrology delay［J］.International Journal of Production Research，2014，52(10): 2915-2930.

［3］SIMANI S，FANTUZZI C.Fault diagnosis in power plant using neural networks［J］.Information Sciences，2000，127(3):125-136.

［4］MCBAIN J，TIMUSK M.System identification for fault detection in variable speed and load machinery［J］.International Journal of Condition Monitoring，2012，2 (2):32-39.

［5］ZHAI S，WANG W，YE H.Fault diagnosis based on parameter estimation in closed-loop systems［J］.Control Theory＆Applications，IET，2014，9(7):1146-1153.

［6］MOHAMMADPOUR J，GRIGORIADIS K，FRANCHEK M，et al.Real-time diagnosis of the exhaust recirculation in diesel engines using least-squares parameter estimation［J］.Journal of dynamic systems，measurement，and control，2010，132(1):011009.

［7］WU A G，FU F Z，TENG Y.Latest estimation based recursive stochastic gradient identification algorithms for ARX models［C］//The 34thControlConference (CCC)，New York:IEEE，2015.

［8］DING F，CHEN T.Performance analysis of multi-innovation gradient type identification methods［J］.Automatica，2007，43(1):1-14.

［9］WU D，LI Y.Fault diagnosis of variable pitch for wind turbines based on the multi-innovation forgetting gradient identification algorithm［J］. NonlinearDynamics，2015，79(3):2069-2077.

［10］WU A G，DONG R Q，FU F Z.Weighted stochastic gradient identification algorithms for ARX models［J］.IFAC-PapersOnLine，2015，48(28):1076-1081.

［11］GOLUB G H，VAN LOAN C F.Matrix computations［M］.4thed.Baltimore，MD:Johns Hopkins Univ Press，2013.

［12］WU A G，WANG Z G.Modified recursive extended least squares identification algorithms［C］//The 25thChinese Control and Decision Conference(CCDC).Gui Yang，2013.

Sensor Fault Detection Based on Hierarchical Stochastic Gradient Identification Algorithm

FU Fangzhou1，WANG Dayi1，2，LI Wenbo1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

A fault detection method based on hierarchical stochastic gradient algorithm is presented for sensor fault.Compared with the least-square identification algorithms，stochastic gradient(SG)identification algorithm has less computational load.The fault detection method is proposed based on stochastic gradient algorithm for the system with limited computing power.The analysis reveals that the higher estimation accuracy of identification algorithm，the higher estimation accuracy of detection method.To improve the accuracy，the hierarchical identification principle is used firstly，and then the unknown true parameters of residual are replaced by the latest estimation.The calculation loads analysis of the proposed algorithm is given.In addition，a simulation example is employed to show the advantage of the proposed approach in sensor fault detection.

hierarchical stochastic gradient;sensor fault;fault detection

TP274

A

1674-1579(2016)04-0012-06

10.3969/j.issn.1674-1579.2016.04.003

符方舟(1990—)，男，博士研究生，研究方向为故障诊断、故障可诊断性评价与设计;王大轶(1973—)，男，研究员，研究方向为故障可诊断性评价与设计、故障诊断算法、卫星制导、导航与控制等;李文博(1984—)，男，博士研究生，研究方向为航天器控制系统可检测性和可隔离性的评价与设计.

*国家杰出青年科学基金资助项目(61525301).

2016-02-23