超静平台动力学建模与解耦控制

王有懿，汤 亮，何英姿

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

超静平台动力学建模与解耦控制

王有懿1，2，汤 亮1，2，何英姿1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100190)

以超静平台在未来高精度航天器主动隔振和精确指向控制中的应用为基础，针对柔性铰形式超静平台的动力学特点以及超静平台基础和载荷扰动作用的影响，建立一般形式的超静平台动力学模型;进一步推导解耦力控制方法，将超静平台由高度耦合的多输入多输出系统变为单输入单输出线性时不变系统，以此消除各支杆之间的相互作用，极大地简化了控制器设计;在此基础上，进行数值仿真分析与验证.仿真结果表明:基于所建立的一般形式超静平台动力学模型，采用解耦力控制方法能够很好地实现超静平台的主动振动控制，并且方法简单易于工程实现.

超静平台;动力学建模;解耦力控制;柔性铰

0 引言

未来空间科学观测、深空激光通信以及高分辨率对地观测等任务对航天器的控制精度和稳定度提出了极为苛刻的指标要求［1-3］.而星上的各种扰动源，如飞轮、控制力矩陀螺、大型天线及太阳帆板的定向驱动装置、斯特林制冷机以及姿轨控发动机等引起的低频振动和高频抖动将会严重影响高精度航天器的控制精度和稳定度，明显降低有效载荷的工作性能.

针对上述问题，国外自上世纪90年代开始研究一种安装于卫星本体和有效载荷之间，具有振动隔离和高精度指向控制的有效载荷搭载平台，称之为“超静平台”［4］，以满足未来航天任务的迫切需求.随后，一些研究机构和学者致力于超静平台相关方面的深入研究.Sullivan等［5］研究了用于从星体扰动和载荷制冷机振动中隔离红外相机载荷，同时实现相机指向调节的超静平台;在他们的研究中，超静平台中每个支杆载荷端的加速度传感器作为反馈测量敏感器，通过音圈电机作动器实现控制.Anderson等［6］采用主动作动器和被动隔振器串联方式，通过支杆中的检波器速度传感器测量反馈，控制压电作动器实现超静平台的主动隔振和抑制.Chen等［7］研究了立方体构型超静平台，基于三对正交的作动器，实现了超静平台六自由度方向的振动隔离，但此平台不具有指向控制和调节功能.Thayer等［8］采用一系列传感器，包括三轴力传感器，LVDT位移传感器以及有效载荷端和基础端检波器速度传感器，研究对比了超静平台在不同传感器配置下的控制方法.Hanieh［9］研究了两种不同形式的超静平台，第一种为柔性超静平台，能够实现六自由度方向的主动隔振;第二种为刚性超静平台，能够提供柔性有效载荷安装界面处的主动阻尼;除此之外，两者都具有指向调节能力.Mclnroy等［10］等通过在超静平台上安装光学指向敏感器，实现了对载荷的两轴主动指向控制及支杆失效后的冗余控制.

上述超静平台支杆与载荷端和基础端的连接大多采用柔性铰连接方式，以此消除普通铰带来的摩擦和间隙影响，从而提高了超静平台的控制精度.然而在超静平台的动力学建模中却较少考虑采用柔性铰引起的超静平台动力学特性变化以及基础和载荷扰动的影响，并且所设计的控制器也大多忽略了各支杆之间的相互耦合作用.

基于此，本文推导了易于实现控制的超静平台动力学模型，通过解耦方法，减少了超静平台各支杆之间的相互耦合作用。首先，建立了包含超静平台基础和载荷扰动的一般形式动力学模型，在此模型中，充分考虑了柔性铰引起的超静平台动力学特性变化;其次，推导了解耦力控制方法，实现了一般形式动力学模型中各支杆之间的控制解耦，在提高超静平台控制性能的同时，极大地简化了控制器设计;最后，给出了数值仿真算例与结果分析。

1 一般形式的超静平台动力学模型

图1给出了一般构型超静平台的结构示意图，其由基础平台、有效载荷平台和6个相同的可伸缩支杆组成.支杆通过两端的柔性铰与基础平台和载荷平台连接.其中，pi(i=1，2，…，6)为6个支杆与载荷平台的连接铰点，bi(i=1，2，…，6)为6个支杆与基础平台的连接铰点.

1.1 支杆动力学模型

如图2所示的第i个支杆，支杆的质量为mi，弹簧刚度为ki，阻尼系数为ci，作动器输出力为fmi，fpi为有效载荷对作动支杆的作用力，pi表示支杆上端与载荷平台连接铰点的位置矢量，bi表示支杆下端与基础平台连接铰点的位置矢量，li表示支杆的长度，lri表示支杆的原始长度.定义向量vi=pi－bi为支杆下端到上端的向量，则支杆的长度，沿支杆的单位方向向量为ui=vi/li.

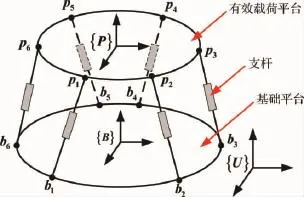
图1 一般构型超静平台Fig.1 A general configuration of ultra quiet platform

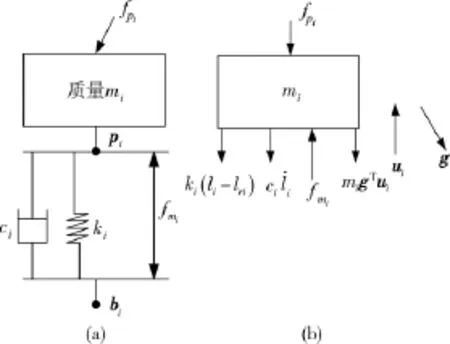
图2 第i个支杆的动力学模型Fig.2 The dynamic model of the ith strut

在支杆动力学建模过程中，由于柔性铰的存在，考虑有效载荷作用力fpi方向近似于第i个支杆的轴向［11］，因此支杆对有效载荷只有6个支杆方向的轴向作用力.

由图2(b)得超静平台6个支杆组合而成的动力学模型为

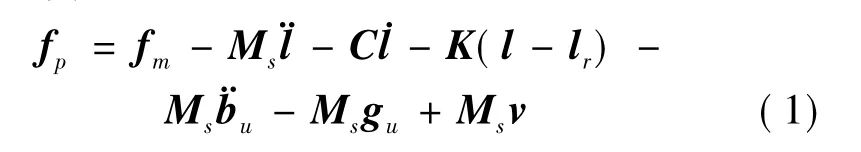
式中:

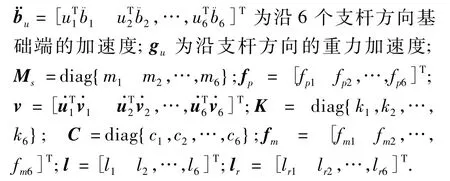
1.2 有效载荷动力学模型

考虑有效载荷为刚体，则动力学方程为

式中:Mx为惯性坐标系中有效载荷的质量/惯量矩阵;为惯性坐标系中有效载荷质心处的广义加速度;F为惯性坐标系中作用于有效载荷质心处的广义力.

在柔性铰形式超静平台中，6个支杆作用于有效载荷质心处的广义力表示为［9］

式中UJ为惯性坐标系中关联支杆运动和载荷运动的雅克比矩阵，左上标符号表示所在的坐标系.

考虑作用于有效载荷的外部扰动力Fd和所受到的重力，联立式(2)和(3)，得到超静平台的动力学模型为

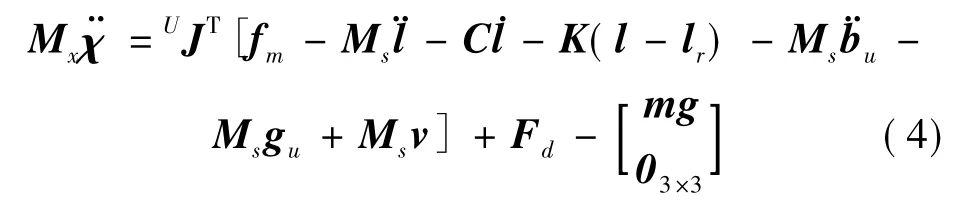
式(4)给出了超静平台的一般形式动力学模型，但并没有完全建立起支杆空间(l)和工作空间(χ)之间的关系.

1.3 支杆空间和工作空间的关系推导

超静平台6个支杆基础端加速度和基础平台广义加速度的关系表示为

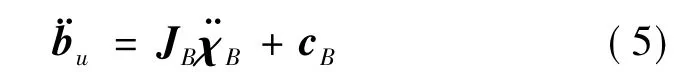
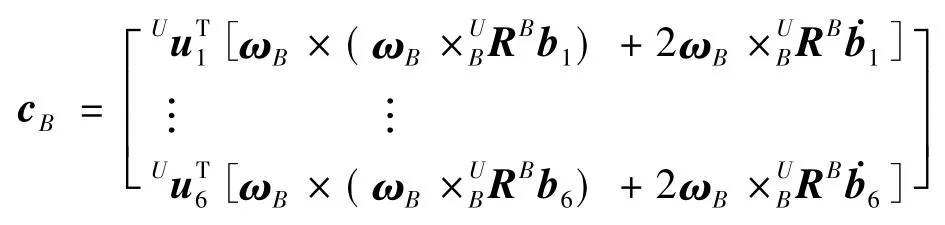
为科式加速度相关矩阵;ωB表示基础平台坐标系{B}相对于惯性坐标系{U}的角速度;UBR为基础平台坐标系{B}到惯性坐标系{U}的转换矩阵，包含了两个相同的3×3维坐标变换矩阵;符号×表示向量的叉乘运算.

有效载荷相对于惯性坐标系的运动与基础平台运动和载荷平台运动的关系表示为

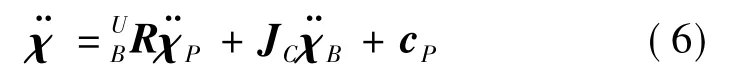
式(6)将惯性坐标系中有效载荷加速度分解为载荷工作空间加速度分量和基础平台工作空间加速度分量.

联立式(5)和(6)，得到支杆空间l和载荷工作空间χ的关系为:

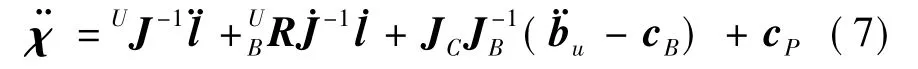
1.4 支杆空间动力学模型

将式(7)代入式(4)，得到支杆空间动力学模型为

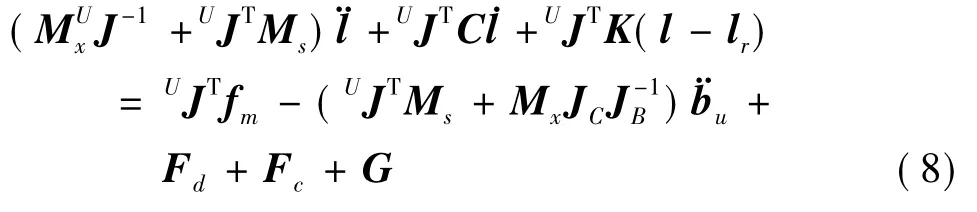
式中:Fc包含所有科氏力相关项;G包含所有重力相关项.

2 超静平台解耦力控制方法

在上述一般形式超静平台动力学模型的基础上，本部分采用解耦力控制方法研究超静平台的六自由度主动隔振问题.

为了实现超静平台六自由度方向的主动隔振，需要最大限度地控制外部扰动从支杆基础端传递到载荷端的力，因而在每个支杆载荷端安装力传感器，则6个支杆力传感器的输出力向量fp为

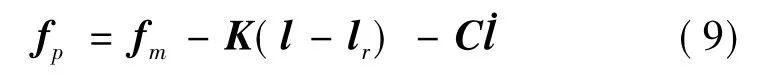
考虑到航天器所受微振动扰振的量级较小，并且柔性铰转动范围有限，因此柔性铰形式超静平台仅仅能够进行小位移运动，方程(8)中的G、JC、JB、J均为常数矩阵;除此之外，在工程上，一定范围频率的小位移运动速度相关的科氏力影响可忽略.通过弹簧伸缩抵消重力作用，lr和G两项也可消除.基于此，方程(8)简化为:

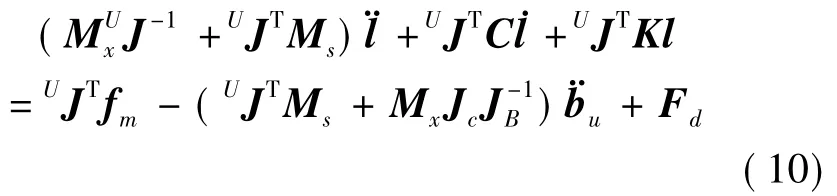
由于式(10)是线性时不变的，联立式(9)和式(10)，并进行Laplace变换，得到支杆作动器输出力向量fm到支杆载荷端输出力向量fp的传递函数为:

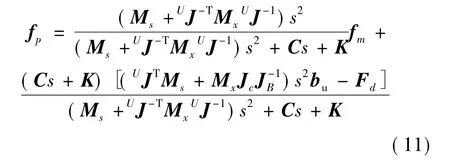
式(11)产生的36个由fm到fp的传递函数是高度耦合的，为了简化控制器设计，需寻求解耦方法.

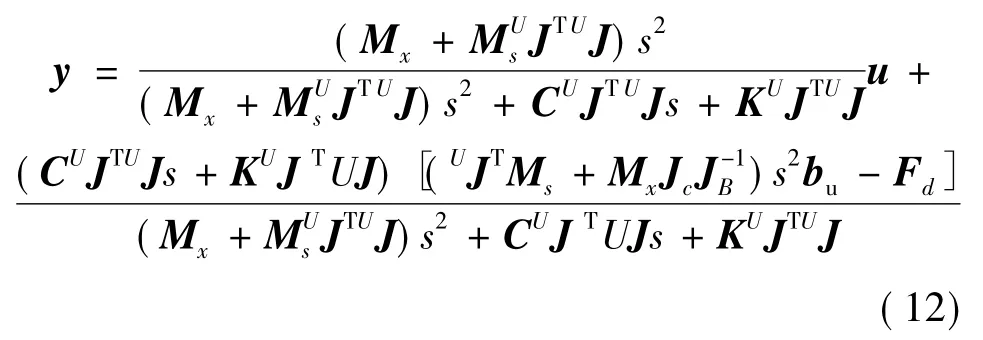
如果式(12)满足以下条件，由u到y的传递函数将会实现解耦，则超静平台由高度耦合的多输入多输出系统变为线性时不变的单输入单输出系统: (1)Mx为对角阵;(2)UJTUJ为对角阵.

对于近似对称的有效载荷，Mx为对角阵，满足上述条件(1);针对经典的“Cubic”构型［9］，如图3中的实线构型，有效载荷的质心与正交支杆形成的立方体中心重合时，UJTUJ为对角阵，满足条件(2).

对经典立方体构型进行局部截取，形成新的立方体构型(如图3中虚线部分)，雅克比矩阵UJ的表达式［12］:

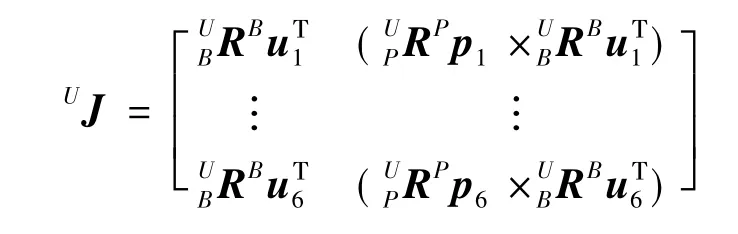
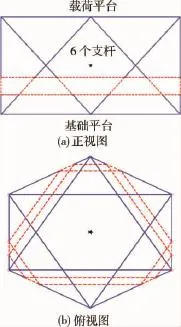
图3 经典立方体构型及新构型(★表示载荷质心位置)Fig.3 Classical cubic configure and new configure (★denotes the location of the payload’s center of mass)

3 仿真算例与分析

针对上述推导的一般形式超静平台动力学模型与解耦力控制方法，进行数值仿真分析与验证.仿真参数为:

支杆与载荷平台连接铰点坐标(载荷平台坐标系):

支杆与基础平台连接铰点坐标(基础平台坐标系):

平台高度h=0.03 m，载荷质心在基础平台坐标系中的位置为［0 0 0.05］m;载荷质量/惯量矩阵为:Mx=diag{18 kg，18 kg，18 kg，0.4 kg·m2，0.6 kg·m2，0.6 kg·m2};支杆质量Ms=0.1 kg，支杆的刚度和阻尼系数分别为k=3 700 Ν/m，c=2.7 Ν·s/m，其仿真结果如图4～5，给出了未解耦和解耦后支杆3作动器输出力到各支杆载荷端力传感器输出力的响应对比图.

由图4的仿真结果可得:即使采用立方体构型的一般形式超静平台动力学模型，各个支杆之间仍是高度耦合的，特别在共振模态附近.图5显示了输入u到输出y的解耦结果;从图中可以看出，输入u产生的响应y与输入u产生的其他响应相差300 dB以上，各个支杆得以完全解耦.尽管此处仅仅显示了输入u产生的6个响应，但其他输入具有相似的解耦特性.

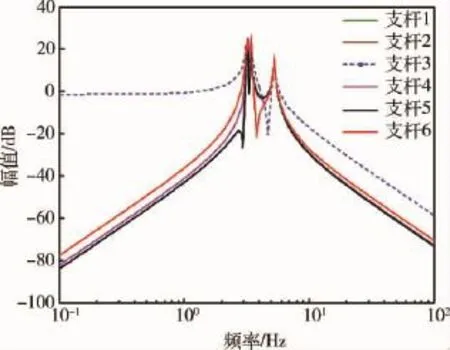
图4 支杆3作动器输出力产生的响应Bode幅值图Fig.4 Bode magnitude plot of response caused by actuator force of strut 3

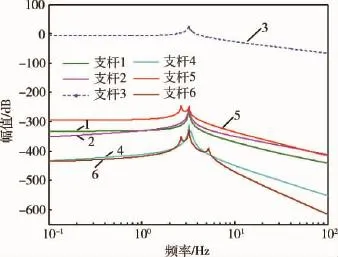
图5 输入u产生的响应Bode幅值图Fig.5 Bode magnitude plot of response caused by input u

图6给出了由支杆作动器输出力到支杆载荷端输出力的开环、耦合力控制、解耦力控制频域对比图;图7给出了超静平台基础施加低频正弦扰动和随机扰动条件下，载荷端力传感器输出力的时域对比图.

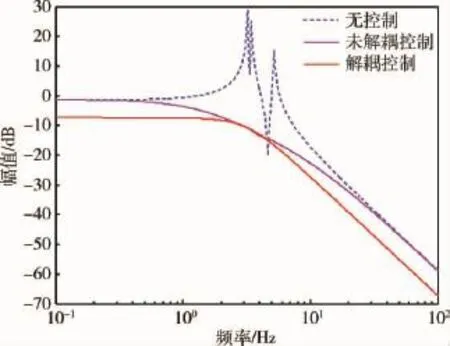
图6 开环、耦合控制和解耦控制对比图Fig.6 The comparison plot with open loop，coupled control and decoupled control

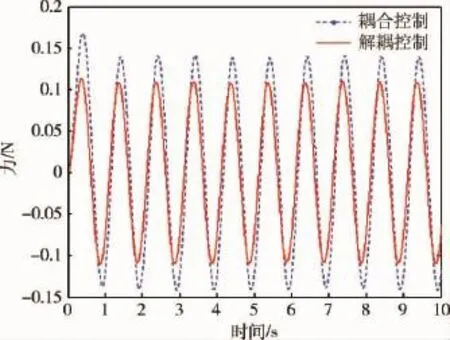
图7 耦合控制和解耦控制时域效果对比图Fig.7 The comparison plot of time-domain effect with coupled control and decoupled control

从图6的仿真结果可以看出:在无控制的开环情况下力的传递是最大的，耦合控制方法能够实现一定频域范围内的主动隔振控制，而相对于耦合控制方法，解耦控制方法可以达到最好的主动隔振效果.图7的时域仿真结果也表明:在低频和随机扰动作用下，相对于耦合控制方法，解耦控制方法会进一步提升超静平台的主动隔振能力.

4 结论

以未来高精度航天器的有效载荷超静平台为研究对象，本文对超静平台动力学建模与控制相关问题进行了深入研究，其主要结论为:

1)考虑柔性铰对超静平台动力学特性的改变，以及超静平台基础和载荷扰动的影响，建立了一般形式的超静平台动力学模型，为控制系统的设计提供精确的动力学模型，

2)推导了解耦力控制方法，实现了超静平台各支杆相互之间的解耦，并通过进一步分析降低了超静平台解耦控制所需满足条件的限制.

3)数值仿真结果表明:采用解耦方法可以很好地消除超静平台各支杆相互之间的耦合作用，并且对于基础扰动的主动振动隔离，解耦力控制方法具有更好的主动隔振效果，且方法简单易工程应用.

本文建立的一般形式超静平台动力学模型和推导的解耦控制方法可以进一步推广应用到超静平台的主动指向控制中.

［1］MEZA L，TUNG F.ANANDAKRISHNAN S，et al.Line of sight stabilization of James Webb space telescope［C］//27thAnnual AAS Guidance and Control Conference.New York:AAS，2005.

［2］SANNIBALE V，ORTIZ G G，FARR W H.A Sub-hertz vibration isolation platform for a deep space optical communication transceiver［C］//Preceding of SPIE Conference on Free-Space Laser Communication Technologies XXI.San Diego:SPIE，2009.

［3］BRUGAROLAS P，ALEXANDER J，TRAUGER J，et al.ACCESS pointing control system［C］//Space Telescopes and Instrumentation:Optical，Infrared，and Millimeter Wave.San Diego:SPIE，2010.

［4］ANDERSON E H，LEO D J，HOLCOMB M D.Ultraquiet platform for active vibration isolation［C］//Symposium on Smart Structures and Materials.San Diego: SPIE，1996.

［5］SULLIVAN J，RAHMAN Z，COBB R，et al.Closedloop performance of a vibration isolation and suppression system［C］//American Control Conference，New York: IEEE，1997.

［6］ANDERSON E H，FUMO J P，ERWIN R S.Satellite ultraquiet isolation technology experiment(SUITE)［C］//American Control Conference.New York:IEEE，2000.

［7］CHEN H J，BISHOP Jr R M，AGRAWAL B N.Payload pointing and active vibration isolation using hexapod platforms［C］//44thAIAA/SAME/ASCE/AHS Structures and Structural Dynamics and Materials Conference.Washington D.C.:AAS，2003.

［8］THAYER D，CAMPBELL M，VAGNERS J，et al.Sixaxis vibration isolation system using soft actuators and multiple sensors［J］.Journal of Spacecraft and Rockets，2002，39(2):206-212.

［9］HANIEH A A.Active isolation and damping of vibrations via Stewart platform［D］.Brussels:Universit’e Libre de Bruxelles，2003.

［10］MCLNROY J E，O’BRIEN J F，NEAT G W.Precise，fault-tolerant pointing using a Stewart platform［J］.IEEE/ASME Transactions on Mechatronics，1999，4 (1):91-95.

［11］MCINROY J E.Modeling and design of flexure jointed Stewart platforms for control purposes［J］.IEEE/ASME Transactions on Mechatronics，2002，7(1):95-99.

［12］MCINROY J E，HAMANN J C.Design and control offlexure jointed hexapods［J］.IEEE Transactions on Robotics and Automation，2000，16(4):372-381.

Dynamic Modeling and Decoupled Control of Ultra Quiet Platform

WANG Youyi1，2，TANG Liang1，2，HE Yingzi1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100190，China)

Based on active vibration isolation and precision pointing control of ultra quiet platform for high precision spacecraft in the future，considering the dynamic characteristics of flexure jointed ultra quiet platform，as well as the effect of base and payload disturbances，the general dynamic model of ultra quiet platform is built.Then the decoupled force control method is derived，and the highly coupled multi-input and multi-output system for ultra quiet platform is converted into single-input and single-output linear time invariant system so that the interaction of different struts is eliminated.The method also greatly simplifies the controller design.On this basis，the numerical simulation analysis and verification are made.The simulation results show that the decoupling force control method using a general dynamic model can achieve good control effect for active vibration control of ultra quiet platform，which is simple and easy to implement.

ultra quiet platform;dynamic modeling;decoupled force control;flexure jointed

V448.2

A

1674-1579(2016)04-0006-06

10.3969/j.issn.1674-1579.2016.04.002

王有懿(1983—)，男，博士，研究方向为航天器主动隔振与精确指向控制;汤 亮(1976—)，男，研究员，研究方向为航天器动力学与控制;何英姿(1970—)，女，研究员，研究方向为控制理论与控制工程。

*国家自然科学基金资助项目(61573060).

2016-03-20