T型测压管路频响特性影响因素的显著性分析

王　栖,胡尚瑜,2,邢心魁

(1.桂林理工大学 土木与建筑工程学院,广西 桂林,541004;2.广西岩土力学与工程重点实验室，广西 桂林,541004)



T型测压管路频响特性影响因素的显著性分析

王栖1,胡尚瑜1,2,邢心魁1

(1.桂林理工大学 土木与建筑工程学院,广西 桂林,541004;2.广西岩土力学与工程重点实验室，广西 桂林,541004)

摘要：基于波动原理开展了T型测压管路系统频率响应特性的实验研究，并根据脉动风压现场实测的基本过程，分别给出了影响测压管路系统频响特性的3个主要因素，每个因素设置了4个水平，基于16个正交实验结果，通过显著性分析，找出了影响因素对测压管路系统频响特性的主次性。结果表明：输入端管路长度对T型测压管路系统频响函数的影响最大，接收端管路长度的影响次之，排水端管长度的变化对测压管路系统的影响最小。

关键词：正交实验;显著性分析;测压管路系统;频率响应

0引言

目前，低矮房屋的风载特性研究方法主要有三种[1-2]：足尺寸建筑现场实测、风洞模拟实验、数值模拟。其中现场实测(简称实测)被认为是获得结构风荷载及风效应最为可靠的方法。考虑到台风暴雨工况下，建筑结构原型表面脉动风压实测管路系统受雨水的影响严重可能造成管路堵塞或损坏风压传感器，风压实测管路系统设计为T型管路，分为原型实测房屋表面的压力端口(金属短管)、连接金属短管与T型三通接头的输入端PVC管、连接微差压感应器与T型三通接头的接收端PVC管、连接U型连通器与T型三通接头的排水端PVC管和压力测量的微差压感应器，其中U型连通器有效的解决了风压实测T型管路系统的排水问题。

电子领域的迅速发展，虽解决了感应器、扫描阀等测量设备的硬件问题，但气流经过T型管路系统至微差压感应器后，压力信号的脉动部分俨然发生了畸变，从而导致脉动风压信号的测量结果失真。虽然近三十年来，国内外学者[3-4]对风洞模型测压实验中直线型管路系统频响特性方面开展相关的研究，重点探讨了直线型管路系统管路长度、直径及限制器等参数对测压管路系统频响函数变化规律的影响。但是风压实测T型管路系统各部分管路长度、直径及T型接头均对频响函数造成影响，而根据波动理论，对于等截面管路系统，气柱的固有频率主要与管路长度相关，为此，本文基于波动理论开展了T型测压管路系统频响特性的实验研究，分析了T型管路系统各部分管路长度对测压管路系统频响特性的影响规律，重点进行了各管路长度影响的显著性分析。

1T型测压管路系统长度对频响函数的影响

1.1T型测压管路系统频响特性实验流程及装置

T型管路的频响函数是进行信号畸变修正和分析的基础，可以通过理论计算或动态标定实验获得[5]。本文实验流程及示意图如图1所示，其中实验装置包括DDS函数信号发生器、TANNOY-501a低频音响、setra264微差压传感器、NI采集系统、定制钢板等,参数设置如表1所示。(1)将定制钢板固定于低频音箱扬声面处且空隙部分用胶棒密封，从而在扬声器与钢板之间形成了一个密封空腔(空腔体积约2×103mm3，它对测压管路系统频响函数的影响可忽略不计)；(2)函数信号发生器可提供一个稳定及标准的正弦电压信号，经功率放大器后传至扬声器，扬声器将电压信号转化为振动压力信号传至该密封空腔；(3)在腔体外平面(即定制钢板，下文均简称为测量面)中心点左右各1cm对称位置处设置直径相同的两个测压孔(直径为12mm)，并通过气动螺纹接头将其与管路系统连接，从而实现测压孔与PVC管内径的一致性和可变性；(4)将一个测压孔洞与感应器通过长度非常短(20mm)的管路相连，其测量到的压力信号数据为参考压力信号；而另一个测压孔洞与感应器通过待标定的实验管路相连，其测量到的压力信号数据为畸变后的压力信号；(4)最终由NI采集系统同步收集这两个振动压力信号。

(a) 动态标定实验流程图　　　　　　　(b) 动态标定实验示意图

仪器名称 精度 参 数DDS函数信号发生器±(1×10-5+10mHz)实验中输入正弦电压信号且频率由5Hz增加到120Hz,增量为5Hz。TANNOY-501a低频音响≤0.7%内置60W功率放大器及低频扬声器setra264微差压传感器±1.0%F.S感应器量程F.S=±1000Pa;压力端口外径4mm长度15mmNI采集系统99.8%采样频率为312.5Hz,各测点样本总长度为3.8×104个数据(约2min)

注:实验温度恒为30℃，湿度恒为50%.

两个测压孔洞距离无限接近时，认为二者孔端的输入信号相同，即认为动态标定实验中测量的参考压力信号等价于待标定的实验管路输入端口的输入信号。如果测压孔洞位置对测量结果的影响很大，那么参考压力信号与待标定实验管路输入端口的输入信号的等效性将是不可行的。以直径30cm的扬声器圆点为中心，在中心1cm东西南北四个方向上各取一点，从水平向顺时针编号K1～K4,并以中心K0为参考，将5个测压孔洞与长度为100mm、直径为4mm的直线型管路进行连接，管路终端与感应器连接，由采集系统同步收集这5个振动压力信号。在0～120Hz频率范围内，K1～K4孔洞测量信号对中心孔洞测量信号的平均误差(取各频率误差结果的平均数)如图2所示，从图2(a)可以看出：K1、K3的测量结果与中心吻合的非常好且脉动压力高达500Pa，说明本文集成的低频音箱更加有效的提高了信号的脉动压力，减小了测试误差(感应器量程为±1Kpa，如果测量信号压力小于100pa，则脉动压力的变化小于感应器的误差变化范围，致使实验结果可靠度下降)；图2(b)可得：距离中心1cm处的各孔洞测量结果相对于中心输入信号的误差很小(基本小于1%)，且各孔洞测量结果相差不大，可见在中心1cm处设置测压孔洞可保证参考测孔与畸变测孔有相同的输入信号，从而认为动态标定实验中参考端压力信号与待标定实验管路输入信号的等效性假设是可行的。

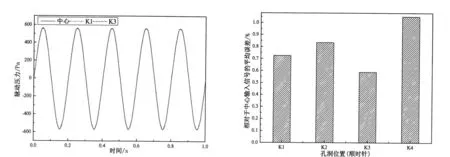
(a) K1、K3压力时称曲线图(激振频率f=5Hz)　　　　　(b) 孔洞位置为信号的影响

(a) 幅频曲线　　　　　　　　　　　　(b)相频曲线

1.2输入端管路长度对频率响应的影响

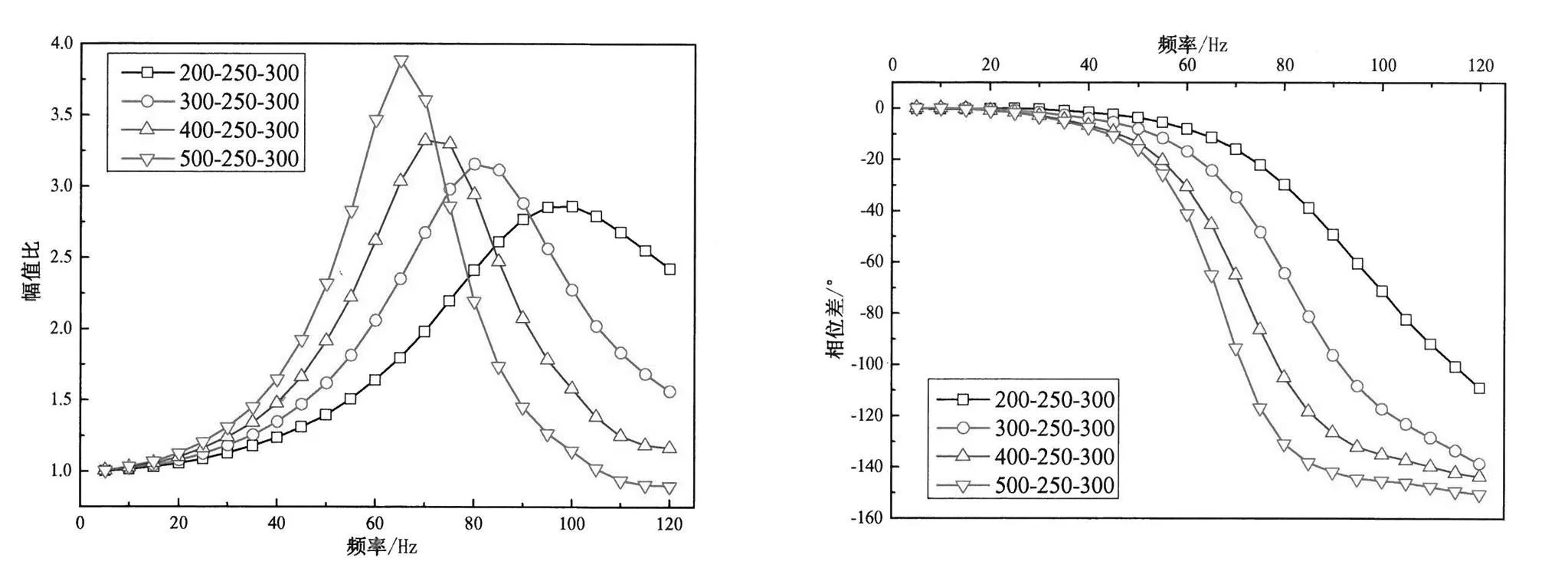
将T型管路中输入端管路、接收端管路、排水端管路记为La-Lb-Lc，由于感应器压力端口外径恒定，故本文所采用的各部分PVC管内径均为4mm。固定Lb-Lc，分别对输入端管路200mm、300mm、400mm和500mm四组工况进行对比分析，实验结果如图3所示，测压管路系统的频响函数均可采用幅频曲线(畸变压力信号和参考压力信号的幅值比)和相频曲线(畸变压力信号和参考压力信号的相位差)表示。从图3(a)可得：在0～20Hz低频范围内，三组工况的幅频曲线变化较为平缓，最大增幅2%；在20～120Hz范围内，La=500mm相比其余三组工况的一阶共振频率显著降低且峰值显著增高，这都说明了随输入端管路长度增加，风压实测T型管路系统固有频率降低，共振效应增强。从图3(b)可知：在0～20Hz低频范围内，三组工况的相位差与频率变化基本符合线性关系；在20～120Hz范围内，四组工况的相位差与频率变化的线性关系逐渐演化为非线性关系。限于篇幅，本文重点讨论幅频曲线部分，即系统幅频特性对实测信号的影响程度。

1.3接收端管路长度对频率响应的影响

固定La-Lc，改变接收端管路分别为250mm、350mm、450mm和550mm的四组工况，讨论其接收端管路长度对频响函数的影响。如图4所示：在0～20Hz低频范围内，三组工况的幅频曲线较为一致，最大增幅1.4%；而随接收端管路长度增加，其发生共振的频率位置分别为100Hz、90Hz、80Hz和70Hz，且共振峰值逐渐增大。表明随接收端管路长度增加，T型管路系统固有频率降低，共振效应增强。

图4　接收管长度不同时管路系统幅频曲线　　　　　　　图5　排水管长度不同时管路系统幅频曲线

1.4排水端管路长度对频率响应的影响

固定La-Lb，对比排水端管路300mm、400mm、500mm和600mm四组工况的实验结果如图5所示，可知：在0～20Hz低频范围内，排水端管路长度增加对T型管路系统频响函数的影响不大(增幅小于0.5%)；但随排水端管路长度增加，T型管路系统固有频率略微降低且共振峰值略有增大。为了进一步说明排水管长度不同时管路系统峰值特性，本文增加了Φ4×700、Φ4×800和Φ4×900三组工况的实验结果如表2所示：随排水端管路长度Lc增加，管路系统的共振峰值先从2.9逐渐增加3.6，而后又逐步降低至2.9。这主要由于随排水管长度增加，T型管路系统中空气的动能增加，沿程损失也逐步增强，在(0mm，600mm)长度范围内增加的动能大于消耗的阻力损失时，T型管路系统共振效应增强；继续增加排水管长度时，管路系统增加的动能小于消耗的阻力损失，T型管路系统阻尼效应增强，从而最终衰减了感应器接收端的压力幅值。

表2　排水管长度不同时管路系统的峰值特性

综上所述，在(0～20Hz)低频范围内，输入端管路长度增加与接收端管路长度增加对管路系统频响函数有略微影响，排水端管路长度增加对其影响不大，故T型测压管路系统具有较好的适应性和测试精度，但各部分管路长度影响测压系统频响函数的主次性仍需进一步分析。

2长度影响因素的显著性分析

2.1长度影响因素的极差分析

根据单因素实验的分析，本文选取输入端管路长度La、接收端管路长度Lb和排水端管路Lc三个影响因素，并根据现场实测经验，各选取四个水平，每组工况做三组平行实验，取平均值作为该工况下一阶频率实验结果，表3给出了16组不同长度组合的测压管路系统和一阶频率实验结果。

极差指一组实验结果中最大值与最小值之间的差值，极差的大小反映了不同长度因素对测压管路系统频响函数的影响程度，分别对一阶频率实验结果中的共振频率与共振峰值做极差分析，得到了各部分管路长度对测压管路系统频响函数的影响如表4所示。其中Lj1表示为第j个因素第一水平对应指标的和，为第j个因素第一水平的指标均值；，其表示为第j个因素的极差。

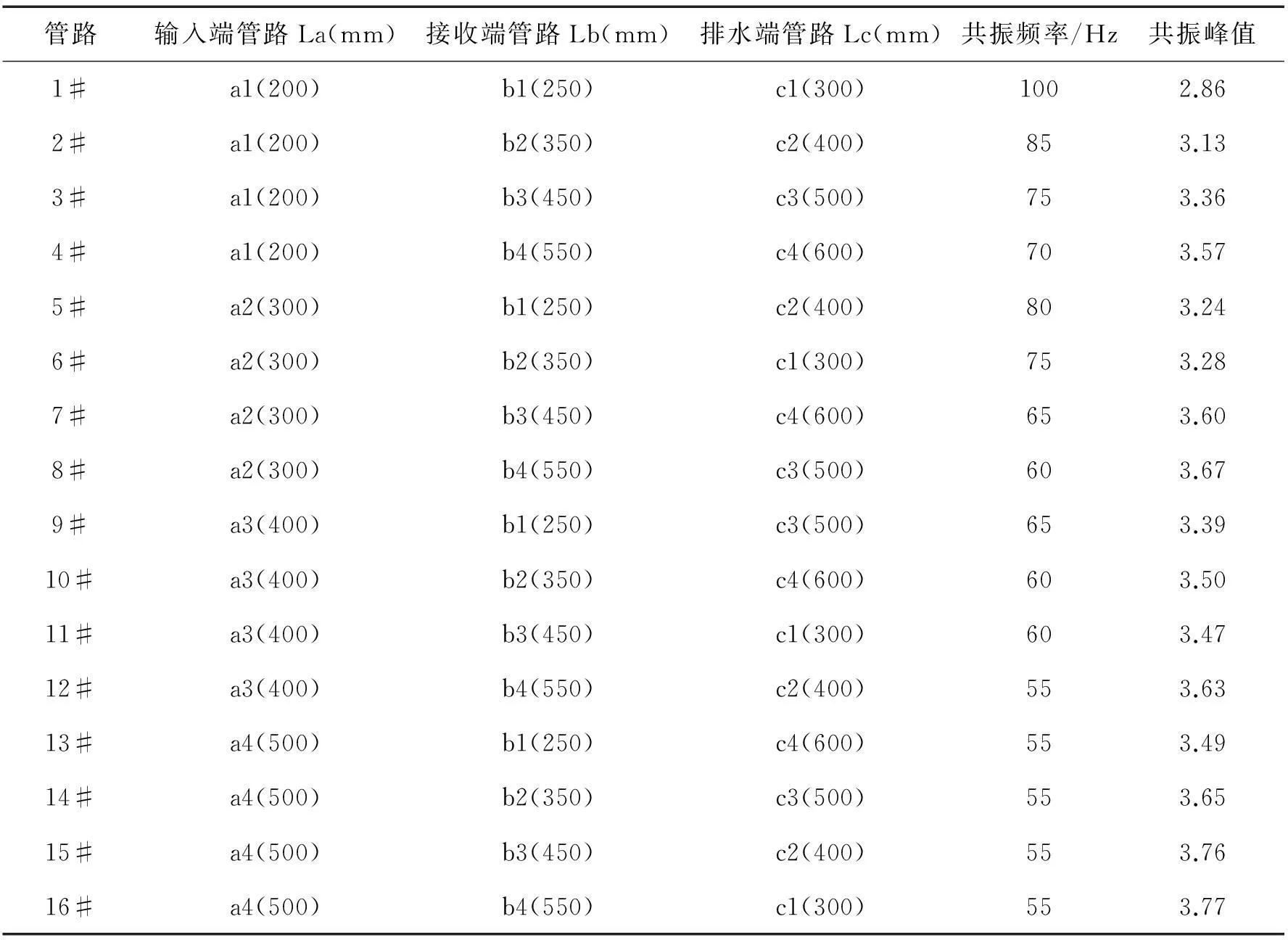
表3　16组测压管路参数及其一阶频率实验结果

表4　.正交实验的极差分析

从表4可知：影响T型管路系统一阶共振频率的主次顺序为输入端管路长度La>接收端管路长度Lb>排水端管路长度Lc，其中输入端管路长度的极差R为27.5，显著大于其他两个因素，因此T型管路系统设计及安装时，为提高系统共振频率，应充分减少输入端管路长度La；影响T型管路系统一阶共振峰值的主次顺序仍为输入端管路长度La>接收端管路长度Lb>接收端管路长度Lc，但输入端管路长度的极差R与接收端管路长度的极差R基本相同，可知输入端管路长度与接收端管路长度的增加对T型管路系统共振效应影响的程度接近。

2.2长度影响因素的显著性分析

根据表5中各因素，计算其偏差平方和如公式(1)，其中r为第j个因素第i个水平的重复数，并引入修正项CT、总的偏差平方和S总及误差偏差平方和Se如公式(2)所示。第j个因素方差之比代表了该因素对指标影响的显著性，其计算公式为Fj=Vi/Ve；其中，Vi为对应因素的方差，Vj=Sj/fj；Ve为误差列的方差，Ve=Se/fe；fj为对应因素的自由度，本文取fj=r-1=e；当Fi>F0.01时，认为第j个因素对频响函数的影响非常显著，当F时，认为第j个因素对频响函数的影响显著，当Fi

(1)

(2)

从表5可以看出：输入端管路长度La对共振频率和共振峰值的影响都非常显著(即方差之比大于显著性水平)；接收端管路长度Lb对共振频率和共振峰值的影响显著，但其对共振频率的方差之比16.2远小于其对共振峰值的方差之比50.7，故可知该段管路长度变化对T型管路系统的共振峰值影响更为重要；值得说明的是，排水端管路长度Lc的增加也对共振峰值影响显著，但其方差比远小于其余两个因素。综上所述，在设计及安装T型测压管路系统时，应充分减少输入端管路长度La和接收端管路长度Lb，在满足暴雨工况下T型管路系统的排水问题时可适当减小管长Lc。

3结论

本文基于波动理论开展了T型测压管路系统频响特性的实验研究，分析了T型管路系统各部分管路长度对测压管路系统频响特性的影响规律，同时采用正交实验方法，重点进行了各管路长度影响因素的显著性分析，结论如下：

(1) T型测压管路系统随各部分PVC管长度增加，固有频率降低，共振效应增强。在(0～20Hz)低频范围内，输入端管路与接收端管路长度增加对管路系统频响函数的影响强于排水端管路长度增加。

(2) 根据本文进行的三因素四水平正交实验结果，得出输入端管路长度对T型测压管路系统频响函数的影响最大，接收端管路长度的影响次之，排水端管长度的变化对该测压管路系统的影响较小，在满足排水的问题时可适当减小该段管长。

(3) 接收端管路长度对T型测压管路系统一阶共振峰值的影响远大于其对一阶共振频率的影响，在现场实测时可适当增加该段管长以防止雨水对风压传感器的影响。

参考文献:

[1] 李秋胜,胡尚瑜.低矮房屋风荷载实测研究-双坡屋面风压特征分析(II)[J].土木工程学报,2012(4):1-8.

[2] 胡尚瑜,李秋胜.台风作用下低矮房屋屋面角部峰值压力实测研究[J].土木工程学报,2012(8):15-24.

[3] 周晅毅,顾明.单通道测压管路系统的优化设计[J].同济大学学报,2003(7):798-802.

[4] 马文勇,刘庆宽.风洞试验中测压管路信号畸变及修正研究[J].流体实验力学,2013(4):71-77.

[5] 韩於羹.应用数理统计[M].北京：北京航空航天人学出版社,2006.

(责任编辑:孙文彬)

Influential Factor Analysis on Frequency Response Characteristicsof the Tee-Junction Pressure Measurement Tubing System

WANG Xi1，HU Shang-yu1,2，XING Xin-kui1,2

(1. College of Civil Engineering and Architecture, Guilin University of Technology,Guilin Guangxi 541004, China;2. Guangxi Key Laboratory of Rock-soil Mechanics and Engineering, Guilin University of Technology,Guilin Guangxi 541004, China)

Abstract:The dynamic frequency response characteristics of pressure measured by Tee-junction tube system were investigated by a dynamic pressure response experimental method based on the wave theory. Three main factors, each one being set to four varying levels based on 16 orthogonal experimental results, affecting the pressure measured tube system frequency response characteristics were given according to the basic process of fluctuating wind pressure field testing. Then the primary and secondary of length influencing factors were found out by significance analysis. The results showed that the primary and secondary sequence of parameters influencing the Tee-junction tube system frequency response function were in the order of the input tube length, the receiver tube length and the drainage tube length.

Key words:orthogonal experiment; significance analysis; pressure measured tube system; frequency response

中图分类号：TU312，V211.73

文献标识码：A

文章编号：1009-7961(2016)01-0038-06

作者简介：王栖(1990-)，男，山西临猗人，在读硕士，主要从事结构风工程研究。

基金项目：广西自然科学基金项目(2013GXNSFBA019232；2015GXNSFAA139251)

收稿日期：2015-10-20