线面分离深化感知——『周长与面积』有效教学策略的思考

蔡水华　丁群俐

“周长与面积”是小学生最初接触到有关图形的计算，在小学数学“图形与几何”板块的教学中占有重要的地位。北师大版教材分别于三年级上、下册编排了认识周长和面积的相关教学内容，在教学情境图中暗含着周长的定义：封闭图形一周的长度。在习题中一般表现为图形所有边长的和，用长度单位衡量；面积指的是物体表面或平面图形的大小，用面积单位衡量。似乎概念十分简单、清晰，但在实际教学中，学生在综合运用“周长与面积”知识解决实际问题时，常常把周长、面积这两个概念混淆，容易出错。因此，“周长与面积”有效的教学策略值得我们思考与研究。

一、缘由分析

分析学生对周长和面积容易混淆的问题，其产生的原因有以下几个方面：

1.教材方面。

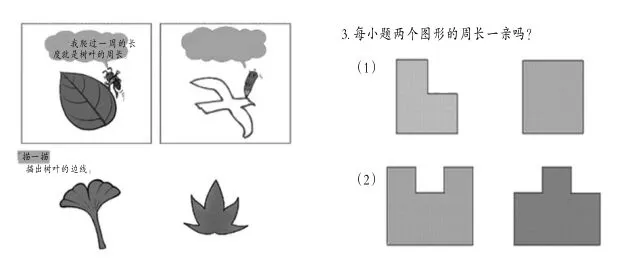
教学素材呈现有共存性。下图为北师大版小学数学三年级上册教材《什么是周长》的情境图和练习用图，学生在材料中同时看到边（周长）和面（面积），其中树叶和着色的平面图形更吸引学生关注的是面，不利于学生对周长的感知与抽象。教学素材中“面”的视觉冲击力干扰着学生对“边”（周长）的注意力。即便教师在教学中有意地强调物体的“边”和“面”，学生也不易将它们真正区分开。因此，教学素材呈现上有共存性，给学生感知概念带来了负面影响。

2.教学方面。

（1）“线”“面”分离不够。在“周长和面积”的教学中，教师应让学生清楚：面积指的是封闭图形围成的面的大小，属于二维空间的度量，有长和宽两个表示的量。而周长是一维空间度量的量，它只有长度，是长度单位的累加。实际教学中，教师常常会呈现具体事物，通过摸、描、画、量、算等方法来引导学生建立周长和面积的概念，尽力让学生知道物体的边框是它的周长。但学生在观察的时候，往往是既看到物体上的“线”（边框），又看到了物体的“面”，即周长和面积同属在一个平面内，不利于周长和面积的区分，干扰了学生的理解。

（2）过多强调公式。在教学中，教师往往会引领学生通过一定的推理得出平面图形的周长、面积计算公式，并理想地认为学生都已经理解、掌握了公式，便不断地引导学生利用公式来解决问题。学生在不断的机械化练习过程中记住的是套搬公式，就不可能去关注周长、面积的本质与内涵。

3.学生方面。

（1）空间思维有局限。周长在小学解释为（封闭）图形一周的长度，关键词是“一周”和“长度”，它们同属于一维空间的测量，但周长却常用在二维图形上，如平面、曲面。也就是说周长是一维的量，却在二维的面里出现和应用，因此，一维的周长与二维的面积容易混淆。同时，小学生的思维以形象思维为主，空间想象能力比较薄弱，往往需要借助直观演示、实践操作等方法感知空间观念。

（2）解题过程多定式。小学生在解题过程中，容易出现“重结果、轻方法”的现象。很多学生面对练习题时，首先想的是如何利用条件中的数据套用公式进行“简单化”、“定式化”解题，而不是分析这些条件、数据的意义与联系，找寻解决问题的突破口与关键点。

二、策略思考

为解决学生在学习过程中由于线、面概念不清而造成的平面图形周长、面积计算混淆问题，笔者对平面图形区分“线”、“面”教学进行探索与研究，旨在教学中给学生以足够的空间经历实践操作、对比辨析、思维内化过程，帮助学生有效建立周长与面积两个不同维度的概念，发展数学思维，提升解决问题的能力。

1.有效素材，利于表象。

有效学习的过程中，新知识与原有知识间的可辨析度，是影响学习的重要变量之一。因此，在教学过程中，教师应关注教学素材的有效选择与呈现，需要有利于唤起学生已有的认识经验，同时也能帮助学生建立并理解周长与面积两个不同维度的概念。

周长属于一维空间（只有“长度”）。在处理教学素材时，就应淡化“面”的干扰，突出长方形四边的长度信息（如下图），给学生以视觉冲击，助其在大脑中形成长方形周长就是四条边长度之和的正确表象。而面积属于二维空间，研究“面”的大小，是由它的长度和宽度两个因素决定的。教师需让学生建立二维表象，弱化四边的长度信息，助其转化为二维信息。（如下图）

2.对比分析，线面分离。

周长与面积混淆的现象集中出现在呈现两者计算公式之后，究其原因，是学生对周长和面积概念的本质缺乏清晰和深刻的理解。因此，在“周长与面积”的教学中，应关注“线”“面”分离，强化对比分析，凸显其本质特征。例如，“周长与面积”的对比课教学：

（1）在黑板上贴一个红色三角形（三角形的一周贴了一圈黑边，如下图），请学生指出这个三角形的周长。

（2）学生指出周长后，教师问：用什么办法可以知道这个图形的周长？

生：用尺子分别量出三角形三条边的长度，再把它们的长度相加。

（3）教师顺势把三角形一周的黑边揭下，粘贴在黑板上连成线，说：“周长是封闭图形一周的长度，就是长长的一条线。”

（4）在分析三角形的周长后，教师问：它的面积又是哪部分呢？

此时，黑板上已形成了鲜明的对比，一边是周长——黑黑的一条线，一边是面积——红红的一整片，给学生造成强烈的视觉冲击，教师通过“长长的线”和“红红的面”直观地展示了周长与面积的本质。

又如，特级教师朱志明在教学《认识面积》之后，强化了面积与周长的对比练习，突出了对周长与面积的本质理解与内在联系，提升了学生的能力。

课件出示（如上图），请同学们比较这5个图形面积的大小，思考并说明理由：

（1）图形______面积相等；

（2）图形①和图形_____面积不相等；

（3）图形①和图形_____面积不相等，理由是_________。

而后，让学生判断“图形的周长相等，面积一定相等。图形的周长大，面积一定大”的正误，并结合图形验证，说说你的理由。

3.直观促思，提升能力。

小学生以直观形象思维为主，思维方法比较单一，抽象概括水平较低，而运用几何直观的方法来“画数学”，可以把文字语言转换成直观符号语言，让学生参与知识的产生和发展过程，体会知识的生成过程，培养和发展学生的数学思维，提升获取知识和解决问题的能力。

问题：把一个边长为8厘米的正方形平均分成四个小正方形，每个小正方形的周长是多少厘米？

让学生再用实物量一量、折一折、剪一剪或在纸上画一画、算一算等过程中，体会图形分剪后的变化及周长的计算方法。通过这样的直观操作，学生对这一知识难点的理解就简单了。

总之，为避免学生对“周长与面积”知识的混淆，在教学中应强化“线”与“面”的分离，深化内涵感知，凸显数学本质，发展学生思维，提升数学能力。