基于衍射成像原理结合相位板抽取的加密方法

巩　琼，王志鹏，杨兴强，张　萍，崔明月，秦　怡

( 南阳师范学院 物理与电子工程学院，河南 南阳 473061 )



基于衍射成像原理结合相位板抽取的加密方法

巩琼，王志鹏，杨兴强，张萍，崔明月，秦怡

( 南阳师范学院 物理与电子工程学院，河南 南阳 473061 )

摘要：为了简化加密系统光学结构以及提高安全性，本文利用相位板抽取方法提出了一种基于衍射成像模型的光学加密方法。该方法在光路中放置三个随机相位板，在输出平面上利用CCD记录衍射光强分布作为密文。在加密时，每次均抽取出其中一个随机相位板，由另外两个随机相位板进行光学加密，一共记录三幅衍射光强分布。解密过程采用数字方法，利用相位恢复迭代算法即可由密文和密钥恢复原始图像。该光学加密方法在加密过程中不需要移动光学器件，只需记录光强分布作为密文，因而便于光学实现。仿真实验表明该光学加密方法可以实现灰度图像的加密，具有多重加密密钥，安全性较高。同时，该加密方法具有一定的抗噪声和剪切攻击的能力，因而该方法可以用于传输环境比较恶劣的条件下。

关键词：傅里叶光学；光学加密；衍射成像；相位恢复算法

0　引言

随着计算机和互联网技术的快速发展，信息安全得到了越来越多的关注。自从Refregier等在1995年提出双随机相位编码(Double Random Phase Encoding, DRPE)[1]光学加密方法以来，光学图像加密技术成为信息安全中一个非常重要研究领域。近年来，国内外专家学者提出了很多种不同的光学图像加密方法[2-10]。这些方法包括：基于联合相关变换器的光学加密[2]，基于分数傅里叶变换的光学加密[3]，基于菲涅尔域的光学加密[4]，基于干涉的光学加密[5]，基于相位恢复算法的光学加密[6]，基于光子计数的光学加密[7]等。其中绝大多数光学加密方法都需要经过光的干涉过程[3-5,7-10]。光的干涉对于系统稳定性的要求非常高，这就给光学加密方法的实现带来了困难。

近年来，为了避免光的干涉过程，进而简化加密系统的光学结构，一些基于光束传播的光学加密技术被提了出来。Chen等人在2010年提出了一种基于衍射成像的光学加密系统[11]，并在随后提出了一系列的改进系统[12-13]。Shi等人在2013年提出了一种基于Ptychography的光学加密系统[14]。在这些光学加密系统中，只需要利用CCD(Charge Coupled Device)等强度感应器件记录多幅光强分布作为加密密文。因此，这些光学加密系统的光学结构被简化了。另外，由于密文只包含输出平面上光场的强度分布，这就破坏了光学加密系统输出与输入之间的线性关系，从而提高了加密系统的安全性。然而，在这些加密方法中，为了记录多幅光强分布，都需要横向(或纵向)移动光学器件，这会增加加密系统的光学实现的复杂程度。

本文在衍射成像原理的基础上，提出了一种基于相位板抽取方法的光学加密。该方法在加密时总共使用三个随机相位板，但在加密过程中每次都抽取掉其中的一个随机相位板，利用另外两个随机相位板得到衍射光场。在输出平面上利用CCD一共记录三幅衍射光场强度分布作为密文。解密时，利用相位恢复算法[15-16]就可以由密文和加密密钥恢复出明文图像。实际上，三个随机相位板都是输入到空间光调制器(Spatial Light Modulator, SLM)上的。因而每次随机相位板的抽取都可以通过控制相应的SLM来实现。正因为如此，我们所提出的方法在加密过程中不需要移动光学器件，这就使得加密系统的光学结构更为简单。

1　理论分析

1.1 菲涅尔衍射

我们所提出的衍射成像光学加密方法是一种基于波束传播的光学加密方法。光波在光路中的传播满足菲涅尔衍射条件，因此某一个光场分布f(x,y)经过距离为d的衍射之后得到的衍射场分布g(μ,ν)满足菲涅尔衍射积分公式[4,17-18]：

其中：f(x,y)表示输入光场分布，g(μ,ν)是衍射场分布，λ是光波波长，j=-1，d是衍射距离，k是波数，k=2π/λ。简便起见，上式也可以表示为

其中：FrTλ,d代表波长为λ的光波经过距离为d的菲涅尔衍射。

1.2 加密过程

该基于衍射成像原理的光学加密原理如图1所示。该加密过程利用一束波长为λ的准直平面光垂直照射输入图像P。该输入图像也称为明文图像。在光路中的相应位置上分别放置三个随机相位板(M1～M3)，在输出平面上利用CCD记录衍射光强分布作为密文图像I。相邻随机相位板以及CCD平面之间的距离分别为d1，d2和d3。为了方便描述，符号(x,y)、(x2,y2)、(x3,y3)和(μ,ν)分别用来表示输入图像、M2、M3和CCD平面的坐标。

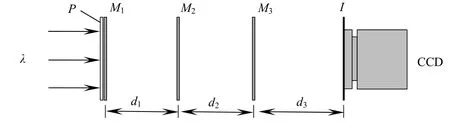
图1　光学加密系统的原理图Fig.1　Schematics of the proposed optical encryption system

在对输入图像进行光学加密的过程中，需要分别抽取出三个随机相位板中的一个，利用另外两个随机相位板进行光学加密，总共记录三个相应的衍射光强分布作为密文。具体的加密过程如下：

首先抽取出第一个随机相位板M1，利用随机相位板M2和M3进行光学加密，CCD记录衍射光强分布I1：

其中符号| |表示取模运算。

然后抽取出第二个随机相位板M2，利用随机相位板M1和M3进行光学加密，CCD记录衍射光强分布I2：

最后，抽取出第三个随机相位板M3，利用随机相位板M1和M2进行光学加密，CCD记录衍射光强分布I3：

至此就完成了光学加密过程，三幅衍射光强分布I1～I3就是加密密文。

1.3 解密过程

由于在光学加密的过程中仅记录衍射光强分布作为密文，而没有记录相位信息，密文和明文间不满足线性关系，因而不能简单的采用加密过程的逆过程来恢复明文图像。要想正确地恢复明文图像，必须利用相位恢复算法。如果已知密文和加密密钥，就可以利用相位恢复算法通过迭代的方法恢复原始图像。

整个解密过程采用数字方式，迭代过程与文献[11-13]中所述方法类似。具体步骤如下：

1) 假定原始图像的初始估计值为Pn(x,y)，n=1。Pn(x,y)可以是随机或常数实值分布。

2) 在抽取出第一个随机相位板的情况下，Pn(x,y)经过正向衍射得到的衍射光场分布为

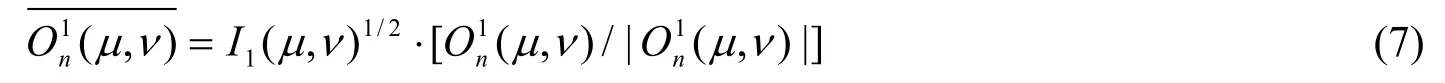
式中符号*表示取共轭操作。

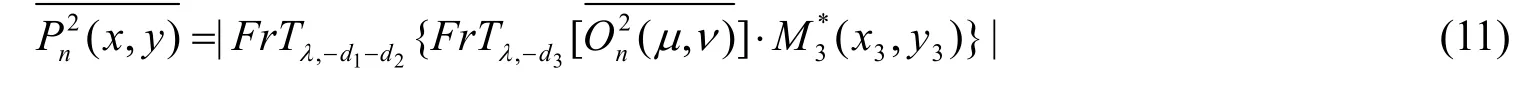
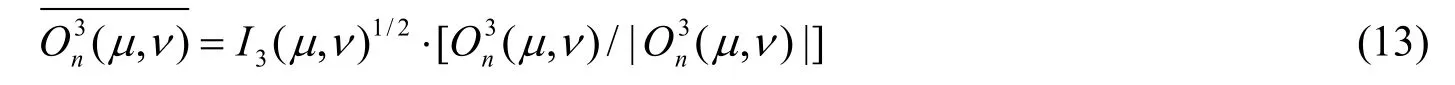
11) 计算Pn+1(x,y )和Pn(x,y)的迭代误差，迭代误差的定义[13]为

如果迭代误差小于设定的阈值δ，则迭代过程结束，明文图像的估计值Pn+1(x,y)就是解密图像。反之，则将Pn+1(x,y)代替式(6)中的Pn(x,y)，继续进行迭代过程。

2　安全性分析

通过前面光学加密过程的介绍可以看到，要想实现正确的解密，除了要掌握密文和三个随机相位板以外，还必须知道在光学加密过程中使用的准直平面光的波长λ以及三个轴向距离d1～d3。这就说明我们所提出的光学加密系统的密钥空间非常大。后面的仿真实验也证明了在任何一个加密密钥有误差的情况下都是无法正确恢复原始图像的。因此，该光学加密系统能够很好地抵御暴力攻击。

众所周知，以双随机相位编码加密系统为代表的一系列光学加密方法[1-4]在本质上是一种线性系统，因而它存在着巨大的安全隐患，容易受到“选择密文攻击”[19]、“已知明文攻击”[20]、“选择明文攻击”[21]和“唯密文攻击”[22]等几种形式的攻击。而我们所提出的这种光学加密系统在输出平面上仅记录光强分布作为密文，因此系统输出与输入之间不满足线性关系，也就很难采用类似的方法破解加密系统。该加密方法也就能够很好地抵御选择密文攻击、已知明文攻击、选择明文攻击和唯密文攻击。

3　计算机实验

为了验证该光学加密方法的有效性和安全性，我们在MATLAB7.1环境下进行了一系列计算机实验。利用提出的光学加密系统对一幅灰度图像(Lena图，256 pixels×256 pixels)进行了加密和解密，其中准直平面光的波长为632 nm，轴向距离d1、d2和d3分别为200 mm、210 mm和220 mm，CCD平面像素间距为8.33 μm。仿真结果如图2所示。图2(a)是原始图像，图2(b)为其中一个随机相位板M1的实部，图2(c)是经过光学加密得到的三幅衍射光强分布中的一个I1。图2(d)是采用正确的密钥经过40次迭代之后得到的解密图像。图2(e)是解密过程中相关系数(Correlation Coefficient, CC)[22]与迭代次数之间的关系曲线。可以看到，经过7次迭代之后，解密图像和原始图像的相关系数已经达到1。这说明该光学加密方法是一种无损方法，并且具有非常快的收敛速度。

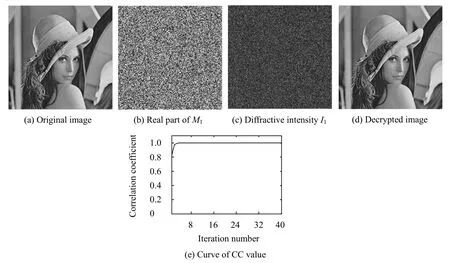
图2　该光学加密系统的仿真结果Fig.2　Simulation results of the proposed encryption system

该系统加密密钥(包括随机相位板、光波波长、轴向距离)的安全性能的仿真结果如图3所示。其中，图3(a)是在一个随机相位板(M2)错误，而其它加密密钥均为正确的情况下得到的解密结果。图3(b)是在迭代解密过程中的相关系数变化曲线。可以看到，即使只有一个随机相位板发生错误，也是无法正确恢复明文图像的，经过2 000次迭代之后解密结果与明文图像之间的相关系数只有0.098。图3(c)是在解密采用的光波波长有10 nm误差，而其它加密密钥均为正确的情况下得到的解密结果。图3(d)是在这种条件下的相关系数变化曲线。由仿真结果可以看到，当光波波长有少量误差的条件下也是无法正确恢复明文图像的。经过2 000次迭代之后解密结果与明文图像之间的相关系数只有0.001 2。图3(e)是在两个随机相位板M1和M2之间的轴向距离(d1)有5 mm误差，而其它加密密钥均为正确的情况下得到的解密结果。图3(f)是相应的相关系数变化曲线。可以看到，在轴向距离有少量误差的情况下同样无法正确恢复明文图像。经过2 000次迭代之后，解密结果与明文图像之间的相关系数为0.007 7。

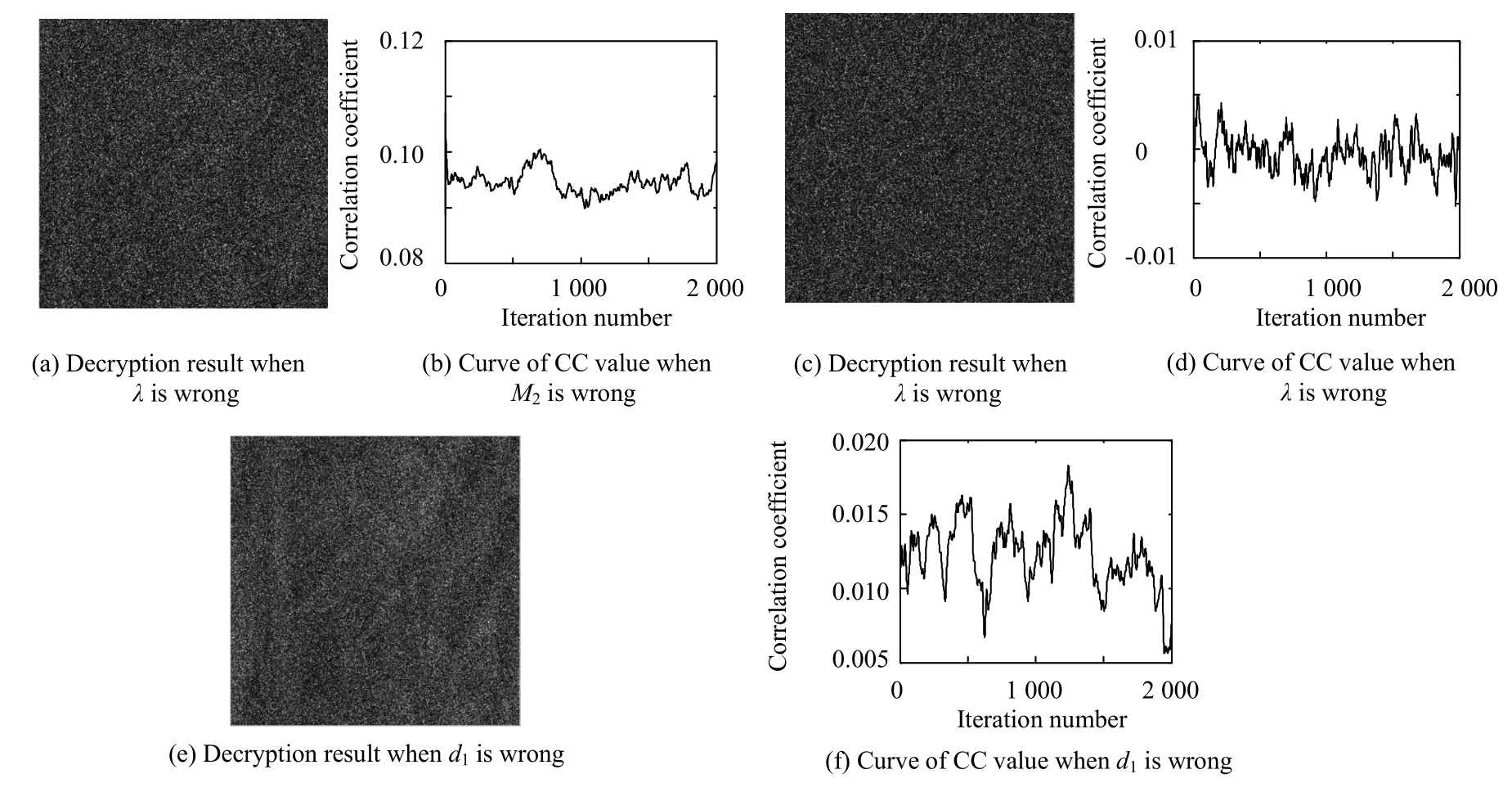
图3　加密密钥安全性能的仿真结果Fig.3　Security performance of the encryption keys

密文在存储和传输的过程中将不可避免地受到噪声污染，因此有必要讨论该加密方法的抗噪声性能。该系统抗噪声性能的仿真结果如图4所示。图4(a)是一个叠加有随机噪声的密文。所叠加的随机噪声[23]分布满足(n(μ,ν)/SNR)×A ，其中n(μ,ν)表示取密文的平均值，SNR是信噪比(在仿真实验中取为4)，A是一个位于[-0.5，0.5]范围内的二维随机分布函数。图4(b)是利用叠加有随机噪声的密文解密得到的恢复图像。图4(c)是在噪声攻击条件下迭代解密过程中的相关系数曲线，经过100次迭代过程之后，恢复图像与原始图像的相关系数为0.983 7。这就说明该加密方法可以很好地抵抗噪声攻击。

图4　该加密方法的抗噪声性能Fig.4　Anti-noise performance of the encryption method

接下来分析该加密方法抵抗剪切攻击的鲁棒性。该方法抵抗剪切攻击的鲁棒性的仿真结果如图5所示。图5(a)，(c)，(e)和(g)分别是丢失10%，20%，30%和40%数据的密文。而图5(b)，(d)，(f)和(h)分别是相应的利用部分丢失的密文解密得到的恢复图像。图5(i)是经过仿真得到的丢失数据比例与恢复图像和原始图像的相关系数之间的关系曲线。通过这组仿真实验可以看到，随着丢失数据比例的增大，恢复图像与原始图像之间的相关系数逐渐减小，而恢复图像的质量也逐渐下降。然而通过仿真结果也可以看到，即使密文丢失40%的数据，我们仍然可以从恢复图像中隐约看出原始图像的轮廓的。这就说明该光学加密方法在部分密文丢失的情况下仍然能够恢复原始图像，具有一定的抗剪切攻击的能力，因而该方法在传输环境比较恶劣的条件下仍然可以实现正确的解密。

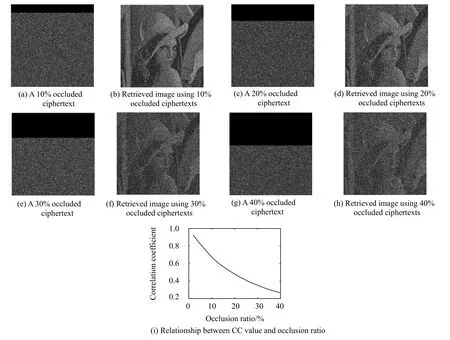
图5　该加密方法抗剪切攻击的鲁棒性Fig.5　Robustness of the proposed method against occlusion attacks

4　结论

本文在衍射成像原理的基础上，提出了一种基于相位板抽取方法的光学加密方法。该加密方法利用CCD器件记录衍射光强分布作为密文，因而不需要利用全息技术来记录密文，这样就简化了系统光学结构。另外，相比于其他基于衍射成像的光学加密系统，我们所提出的方法只需要通过抽取不同的随机相位板来实现光学加密过程，实际上随机相位板的抽取可以通过控制SLM来实现，因而在光学加密过程中不需要横向或轴向移动光学器件，这样就进一步简化了系统结构，便于系统实现。通过一系列计算机实验可以看到，该加密方法能够实现灰度图像的光学加密，具有多重加密密钥，并且可以在一定程度上抵御噪声和剪切攻击，具有较高的安全性。

参考文献：

[1] Refregier Philippe，Bahram Javidi. Optical image encryption based on input plane and Fourier plane random encoding [J]. Optics Letters(S0146-9592)，1995，20(7)：767-769.

[2] Takanori Nomura，Bahram Javidi. Optical encryption using a joint transform correlator architecture [J]. Optical Engineering (S0091-3286)，2000，39(8)：2031–2035.

[3] Unnikrishnan G，Joseph J，Singh K. Optical encryption by double-random phase encoding in the fractional Fourier domain [J]. Optics Letters(S0146-9592)，2000，25(12)：887-889.

[4] SITU Guohai，ZHANG Jingjuan. Double random-phase encoding in the Fresnel domain [J]. Optics Letters(S0146-9592)，2004，29(14)：1584-1586.

[5] ZHANG Yan，WANG Bo. Optical image encryption based on interference [J]. Optics Letters(S0146-9592)，2008，33(21)：2443-2445.

[6] SITU Guohai，ZHANG Jingjuan. A lensless optical security system based on computer-generated phase only masks [J]. OpticsCommunications(S0030-4018)，2004，232(1/6)：115–122.

[7] Elisabet Pérez-Cabré，Myungjin Cho，Bahram Javidi. Information authentication using photon-counting double-random-phase encrypted images [J]. Optics Letters(S0146-9592)，2011，36(1)：22-24.

[8] CHEN Linfei，ZHAO Daomu. Optical image encryption based on fractional wavelet transform [J]. Optics Communications (S0030-4018)，2005，254(4/6)：361–367.

[9] 刘效勇，曹益平，卢佩. 基于压缩感知的光学图像加密技术研究 [J]. 光学学报，2014，34(3)：0307002. LIU Xiaoyong，CAO Yiping，LU Pei. Research on Optical Image Encryption Technique with Compressed Sensing [J]. Acta Optica Sinica，2014，34(3)：0307002.

[10] 秦怡，李婧，马毛粉，等. 一种基于随机相位板复用的光学多二值图像加密系统 [J]. 光学学报，2014，34(3)：0307001. QIN Yi，LI Jing，MA Maofen，et al. System for Optical Multiple Binary Image Encryption by Random Phase Mask Multiplexing [J]. Acta Optica Sinica，2014，34(3)：0307001.

[11] CHEN Wen，CHEN Xudong，Colin J R Sheppard. Optical image encryption based on diffractive imaging [J]. Optics Letters(S0146-9592)，2010，35(22)：3817–3819.

[12] CHEN Wen，CHEN Xudong，Colin J R Sheppard. Optical double-image cryptography based on diffractive imaging with a laterally translated phase grating [J]. Applied Optics(S1559-128X)，2011，50(29)：5750–5757.

[13] CHEN Wen，CHEN Xudong，Arun Anand，et al. Optical encryption using multiple intensity samplings in the axial domain [J]. Journal of the Optical Society of America A(S1084-7529)，2013，30(5)：806–812.

[14] SHI Yishi，LI Tuo，WANG Yali，et al. Optical image encryption via ptychography [J]. Optics Letters(S0146-9592)，2013，38(9)：1425-1427.

[15] Gerchberg R W，Saxton W O. A practical algorithm for the determination of phase from image and diffraction phase pictures [J]. Optik(S0030-4026)，1972，35(2)：237-246.

[16] Fienup J R，Phase retrieval algorithms：a comparison [J]. Applied Optics(S1559-128X)，1982，21(15)：2758-2769.

[17] Goodman J W. Introduction to Fourier Optics：2nd ed [M]. McGraw-Hill，1996：66-73.

[18] QIN Yi，WANG Zhipeng，GONG Qiong. Diffractive-imaging-based optical image encryption with simplified decryption from single diffraction pattern [J]. Applied Optics(S1559-128X)，2014，53(19)：4094-4099.

[19] Arturo Carnicer，Mario Montes-Usategui，Sergio Arcos，et al. Vulnerability to chosen-cyphertext attacks of optical encryption schemes based on double random phase keys [J]. Optics Letters(S0146-9592)，2005，30(13)：1644-1646.

[20] 彭翔，张鹏，位恒政，等. 双随机相位加密系统的已知明文攻击 [J]. 物理学报，2006，55(3)：1130-1136. PENG Xiang，ZHANG Peng，WEI Hengzheng，et al. Known plaintext attack on double random phase encoding encryption technique [J]. Acta Physica Sinica，2006，55(3)：1130-1136.

[21] 位恒政，彭翔，张鹏，等. 双随机相位加密系统的选择明文攻击 [J]. 光学学报，2007，27(5)：824-829. WEI Hengzheng，PENG Xiang，ZHANG Peng，et al. Chosen-Plaintext Attack on Double Random Phase Encoding Encryption Technique [J]. Acta Optica Sinica，2007，27(5)：824-829.

[22] 彭翔，汤红乔，田劲东. 双随机相位编码光学加密系统的唯密文攻击 [J]. 物理学报，2007，56(5)：2629-2636. PENG Xiang，TANG Hongqiao，TIAN Jindong. Ciphertext-only attack on double random phase encoding optical encryption system [J]. Acta Physica Sinica，2007，56(5)：2629-2636.

[23] CHEN Wen，CHEN Xudong. Space-based optical image encryption [J]. Optics Express(S1094-4087)，2010，18(26)：27095-27104.

本期组稿：杨淇名

责任编辑：谢小平

英文编辑：庞洪

An Encryption Method Based on Diffraction Imaging Principle and Phase Mask Removal Method

GONG Qiong，WANG Zhipeng，YANG Xingqiang，ZHANG Ping，CUI Mingyue，QIN Yi
( College of Physics and Electronic Engineering, Nanyang Normal University, Nanyang 473061, Henan Province, China )

Abstract:In order to simplify the optical structure of the encryption system and enhance the security, an encryption method based on diffraction imaging principle is proposed by using phase mask removal method. In the proposed optical encryption approach, three random phase masks are placed in the optical path, and a CCD camera in the output plane is used to record the diffraction intensity distribution as ciphertext. In encryption, one of the three random phase masks is removed at a time, and the other two masks are used for optical encryption. Accordingly, three diffraction intensity distributions are recorded in all. Decryption process uses digital method. The original image can be retrieved from the ciphertext and security keys by means of phase retrieval algorithm. The encryption could be achieved without any movement of the optical devices, and only intensity distributions are recorded as ciphertext, thereby facilitating the optical implementation. Simulation results show that the proposal can achieve gray image encryption, and have multiple encryption keys. As a result, high security is gained. Meanwhile, the proposed approach has the ability to resist noise attack and occlusion attack, which makes the proposal suitable for harsh transmission conditions.

Key words:Fourier optics; optical encryption; diffraction imaging; phase retrieval algorithm

作者简介：巩琼(1982-)，女(汉族)，甘肃天水人。讲师，主要研究工作是信息光学与信号处理。E-mail：27191249@qq.com。

基金项目：国家自然科学基金项目(61505091)；河南省科技厅基础与前沿计划项目(142300410454)；河南省高等学校重点科研项目(16B510005, 16A416010)；南阳师范学院青年基金资助项目(QN2015009)

收稿日期：2014-12-11； 收到修改稿日期：2015-04-03

文章编号：1003-501X(2016)01-0088-07

中图分类号：TP751.2; O438.2

文献标志码：A

doi：10.3969/j.issn.1003-501X.2016.01.016