结合先验信息的渐近式角点定位
2016-04-01刘文静付鲁华郭有为天津大学精密测试技术及仪器国家重点实验室天津300072
王 仲,刘文静,付鲁华,郭有为( 天津大学 精密测试技术及仪器国家重点实验室,天津 300072 )
结合先验信息的渐近式角点定位
王仲,刘文静,付鲁华,郭有为
( 天津大学 精密测试技术及仪器国家重点实验室,天津 300072 )
摘要:针对批量微小型二维工件在视觉检测中角点的定位,提出一种渐近式分步提取方法。该方法以图像单像素轮廓上固有的几何关系为先验信息,首先在轮廓序列中锁定本次待测角点的存在区域,然后根据角点特征灵活设置响应函数检测角点,并对其精确定位及时排除伪角点,之后重新锁定区域。这一过程循环渐近,直至将所有角点检测出。实验结果表明,对同一工件不同位姿多次采像检测,角点间距的标准差在0.5 pixel以内,重复性高。与Harris角点检测、CSS角点检测算法比较,对视场内杂质背景的抗干扰性强,定位准确、快速。该角点定位方法在微小型二维工件的大批量高速检测中,具有明显优势。
关键词:角点定位;先验信息;批量微小型工件检测;机器视觉
0 引言
对大批量微小型二维零件的高速、高精度视觉检测而言,图像处理是其核心技术,影响着整个设备的速度、精度、以及整机复杂程度。工件上的特殊点通常既是功能、工艺的关键点,也是测量的关键点。在图像处理中,它们常常表现为角点。准确的角点检测对完成许多视觉任务至关重要,如尺寸测量、图像匹配、图像识别、检索等。
现有的常规角点检测算法分为两大类:第一类基于图像的灰度信息提取角点,如Harris、SUSAN等算法[1-2]。这类算法可在亚像素级提取角点;但通常需要处理大量数据,计算复杂度高,并对图像旋转等几何变换鲁棒性较差。另一类是依据图像的轮廓特征提取角点,典型的有CSS算法以及对CSS算法的一系列理论改进研究[3-5]。这类算法的定位准确性很大程度上依赖于预处理得到的边缘轮廓。相比于第一类,计算复杂度有所降低,对于杂质点干扰的抵抗力有所提高,更能适应目标在图像中位置改变时其角点的提取。两类常规算法,提取的仅仅是符合角点特征的点;而机器视觉检测中,需要的是这其中对测量有意义的目标角点。比如杂质角点符合角点特征但无意义。所以,在背景复杂的视场中,对于角点定位重复性以及时耗要求严格的检测中,两类传统方法难以胜任。以“汽车卡簧高速全自动检测分选”项目为例,为了降低对送至检测位的工件的机械定位难度,图像处理算法需要对在检测位呈现多种位姿的工件均有适应性。实际情况下,待测件卡簧概率性贴附于检测位的限位边框;并且设备应用于工业现场,视场中不可避免的沾染灰尘等杂质。最终造成角点的多样性、冗余性、位置不确定性。如此复杂的情况下,利用常规角点检测算法,有以下不足之处:第一,会将图片中所有角点同时提取出。加之设备连续运行检测,背景时变,与多位姿工件共同形成的角点繁乱无序。欲从大量无序角点中筛选目标角点,异常棘手;第二,在全图范围内判别角点,速度难以保证;第三,全幅中使用一种算法判别工件中不同类型的目标角点,针对性差。总之,常规检测算法难以准确定位目标角点。
自动化检测设备通常作用于大批量检测对象,针对特定规格的零件,先验信息是一种不可丢弃的宝贵资源。若加以利用,会给图像处理带来极大的方便[6-7]。本文充分利用零件的几何尺寸与形状特征数据,提出一种分步渐近式角点定位方法:在预处理得到工件全轮廓序列后,拟定初始基准点,确定约束条件进行边缘轮廓分割,从而锁定角点搜索范围。根据待测角点特征灵活设计判别方法作用于本次范围内,检测角点、剔除伪角点、优化位置。以检测出的角点为基础,继续锁定下一次角点检测范围,直至找全所有目标角点。基准的选取、检测区域的锁定、判别方法的拟定、角点的去伪均基于先验信息。
1 锁定角点检测的关注区域
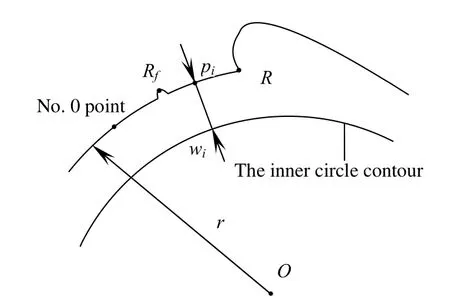
原始工件图片,经预处理[8]得到单像素边缘轮廓。按逆时针跟踪顺序从起点开始,存储边缘点在图像坐标系中的x、y坐标值。如图1,得到轮廓序列L。L中有许多不是角点存在的区域,本文首先结合先验信息锁定角点检测的关注区域。
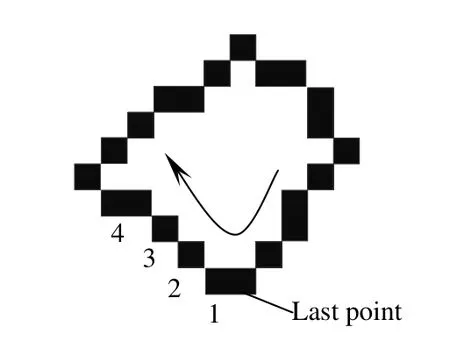
图1 逆时针方向跟踪Fig.1 Tracking contour anticlockwise
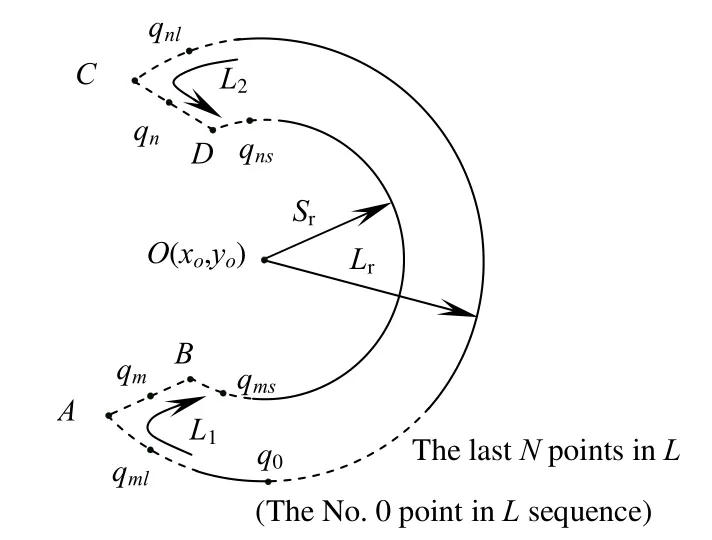
图2 锁定角点检测范围Fig.2 Getting the region where corners exist
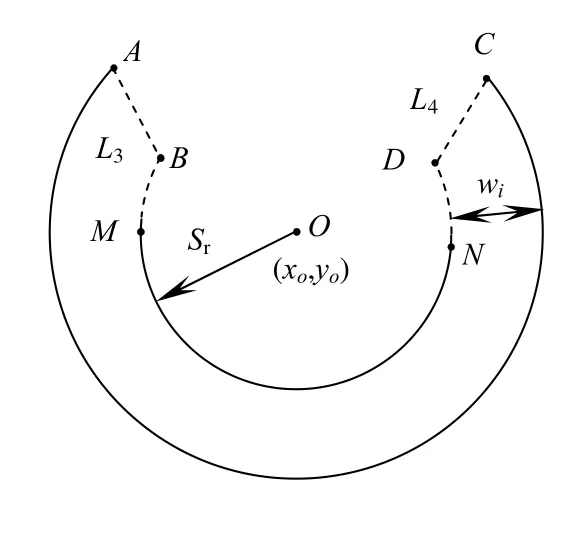
以图2卡簧工件的轮廓为例,最终目的是定位出A、B、C、D四个角点。利用L中倒数N个点的坐标,依据最小二乘法拟合圆心、半径。与先验信息比较,若所得半径在(Lr-δ,Lr+δ)内,认为相应圆心(xo,yo)为内外同心弧所对应的圆心,并作为基准点O。其中δ为若N个点均在外弧段上时,拟合半径与标准外径Lr的最大偏差。否则,利用L中初始N个点重新拟合。然后从轮廓序列中第0点开始,以步进k确定点集Q={q0,q1,…,qt},其中qi为L中第i×k个点。k小于A、B间距离|AB|(以像素表示):

以保证Q集中必然有点在AB、CD范围内。M为轮廓点序列总数,t满足:

计算Q集中所有点到O的距离di:

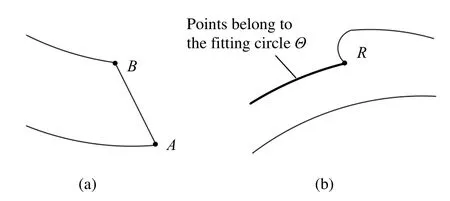
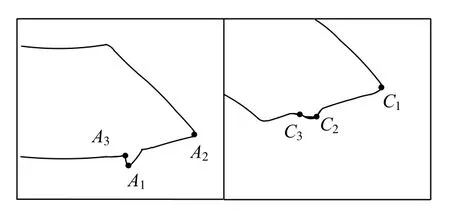
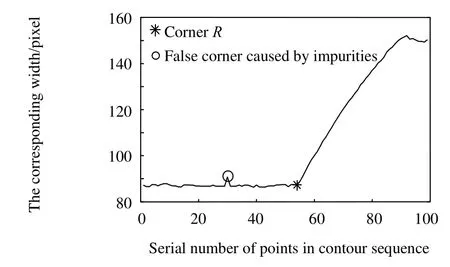
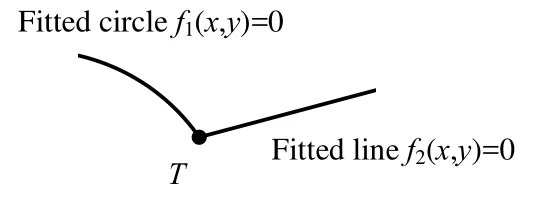
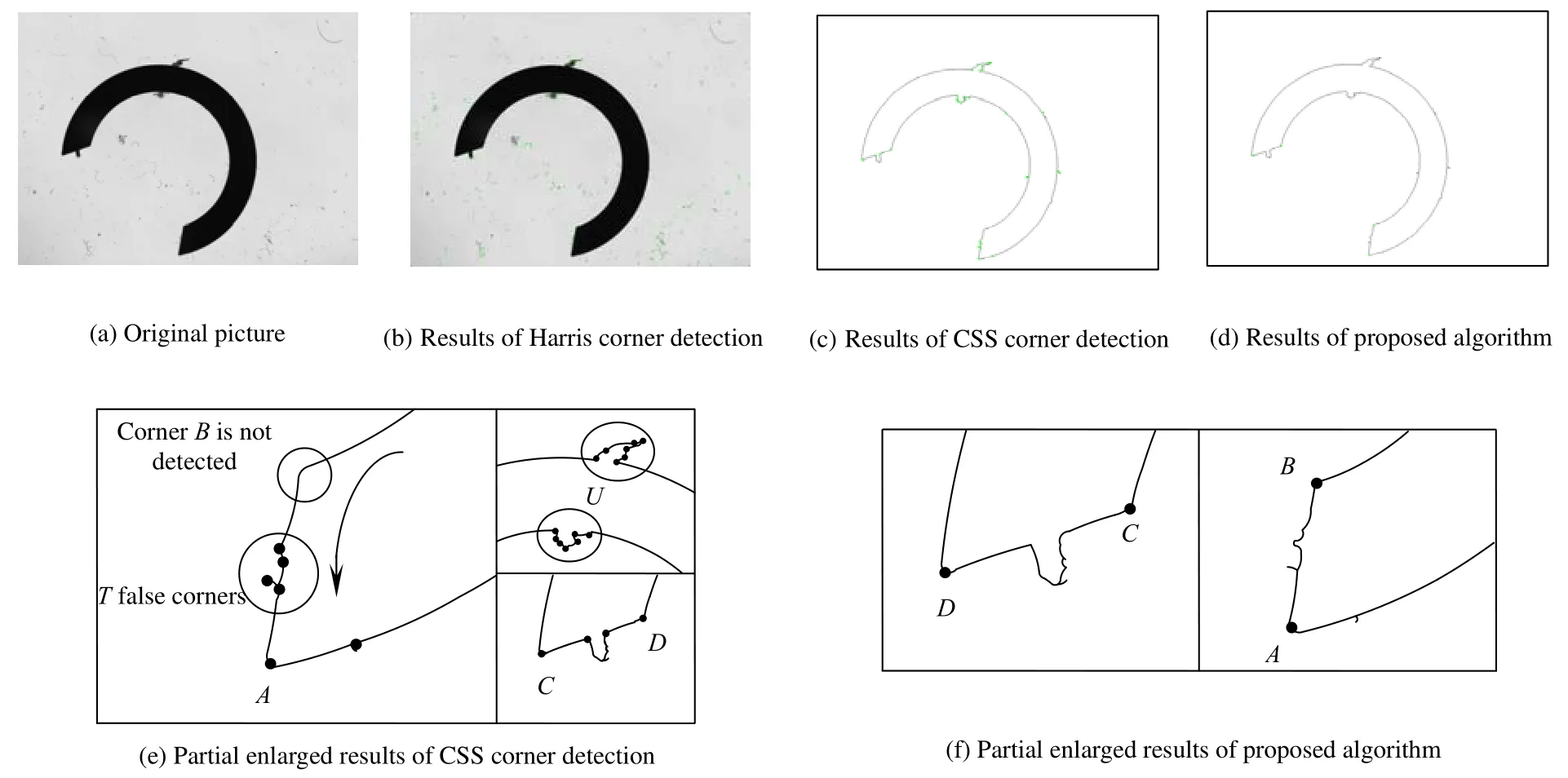
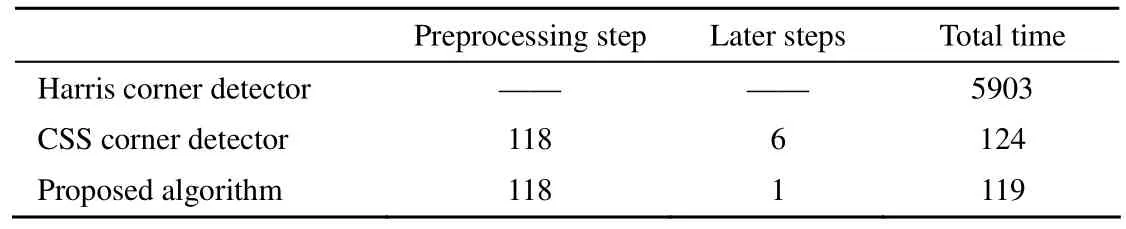
xi×k、yi×k分别为qi的横纵坐标。对应保存成距离集D={d0,d1,…,dt}。从i=0开始遍历D集,寻找第一个dm,使其满足Sr 记录m、ml、ms、n、nl、ns。将原轮廓序列中顺序为mlk-0.5k 到msk+0.5k 段内的点确定为待测角点所在的局域序列L1,将nlk+0.5k到nsk-0.5k 段内的点确定为L2。L1、L2即是接下来角点提取所作用的范围。 确定本次检测范围后,考虑局域轮廓序列中各类角点的特征,先将特征最明显,最具有区分度的角点定位出来。比如:即使工件制造误差很大,依然是锐度最大的点,如图3(a)中点A;处于简单拟合曲线断开处的角点,如图3(b)中点R。 2.1 支撑臂夹角定位锐度最大的角点 对于图3(a)中A、B两点来说,B为钝形角点,A的锐度最大,不易受杂质点干扰,具有更好的辨识度。这是选择以支撑域内支撑臂夹角作为响应函数定位角点的前提保证。以轮廓点pi为中心,其k个有序前点和k个有序后点组成pi的2k+1支撑区域。求出pi在支撑域中的角度θi: 图3 角点类型举例Fig.3 Some kinds of corners 图4 θi极小值角点Fig.4 Corners with minimum θi 另外,支撑区域k的选取是算法成功的关键。在角点分布不密集、待测角点数量已知且锐度明显区别于周围轮廓点时,k可取5~7。同时参考RJ算法[9]和The-Chin算法[10]两种具有代表性的支撑域选取原则。在局域轮廓内判别此类锐形角点,采用点到弦距离累加法[11]以及文献[12]提到的方法也非常有效。 2.2 检测拟合曲线断开处的角点 图5中,R处于轮廓点是否在圆O上的分界处,圆上的点到内圆宽度在一定范围内。因此,可以从搜索区域中第0点开始,计算每个点pi到内圆轮廓的宽度wi,并绘制i—wi曲线,如图6。直至i=t时满足: 则初步确定第t点即为角点R。wthreshold是根据先验信息获得的环允许宽度的最大值。图6所示,根据式(7)、(8)角点R处曲线转折,可以明显区别于非角点。之后再在t点附近精确定位角点,参看第3节。式(8)有效保证了工件上沾染小尺寸异物形成的伪角点被剔除,如图5中Rf。 图5 拟合曲线断开处的角点Fig.5 Corner at disconnect of the fitting curve 图6 轮廓点与其对应宽度曲线Fig.6 The curve of contour points andtheir corresponding width 在第2节定位角点的基础上,如果有必要进一步优化其位置,可采用简单响应叠加来精确定位角点。 其中:G1(i)、G2(i)、……分别为一种角点判定方式。充分利用角点的多种几何特征,将两种及以上响应方式叠加,加强角点响应,弱化干扰。简单举例,如图7,轮廓为搜索区域,角点T满足两个特征:①其支撑臂夹角具有局域极小值;②T是拟合圆与拟合直线的交点。设已利用条件①(2.1节方法)拟定响应函数G1(i)对T粗略定位。之后,取前后远离T的点拟合得到圆方程f1(x,y)=0与直线方程f2(x,y)=0,拟定响应函数G2(i): 图7 多特征角点Fig.7 Corner with multiple features 角点T满足G2(t)=minG2(i)。G1(i)、G2(i)均在角点处取得最小值,故设定α、β同号。再根据大量试验获得两响应函数区别该角点与其他轮廓点时的敏感程度,为α、β赋权值。这里不妨均设为1,则: 在序列中对初步确定的T前后第i个点求G(i),i∈[1,k]。根据G(t)=minG(i),最终准确定位角点T。 实验选用合格卡簧为被测件,图8(a)所示;检测设备为实验室自行研制的分选仪。成像系统由维视图像生产的MV_300SC相机配合艾菲特双远心镜头BT_2348构成,如图8(b),采用LED平板光源背光照明,图8(a)。 如图9,卡簧的检测参数有拟合内径Sr、BD间距|BD|、AB与CD的对称性。且卡簧在检测位以各种位姿随机分布。分析检测需求,可知点A、B、C、D均为待定位角点。设计检测算法,步骤如下: 1) 以第1节方法,从全轮廓序列L中锁定搜索范围L1、L2; 2) 采用2.1节求支撑臂夹角取最小值的方法,检测角点A、C; 3) 拟合内径Sr:从全轮廓序列中确定A点往后第k个点M,C点往前第k个点N。利用MN之间的序列点采用最小二乘法拟合内圆,得到半径Sr以及圆心O(xo,yo); 4) 确定检测B、D的搜索范围L3、L4:在L1中取A点以后轮廓段作为L3,同理从L2中得到其子集L4; 5) 利用2.2节方法,以L3、L4为搜索序列,求搜索范围里各个点pi到外圆轮廓的距离wi,粗略定位角点B、D; 6) 利用第3节方法将两种响应叠加,优化B、D点坐标。 图8 实验检测系统Fig.8 Picture of detection system 图9 实验参数示意图Fig.9 Picture show detected parameters 4.1 本文算法性能验证 将工件在视场内任意旋转、平移,处理得到10组角点间距|BD|、|AC|的测量值,并计算10组数据的极差与标准差。以像素为单位列于表1。 表1 |BD|、|AC|测量数据与统计结果Table 1 The experimental data and statistical results of |BD|、|AC| pixel 由于不同位姿时角点在图像坐标系中的坐标值没有可比性,所以,|BD|、|AC|距离的稳定性可作为角点提取是否准确的评判标准。采用双远心镜头,镜头畸变小于0.05%,认为视场内各处像素当量均一。 可见,不同位姿多次测量的统计结果均在一个像素以内。本文提出的方法具有很好的重复性、稳定性,对工件的旋转位姿具有适应性。 说明:在预处理中得到误差允许范围内的“准确轮廓”是本文算法成功的前提保证。预处理不当,上述10组数据将会产生大的误差,这里不做详细分析。 4.2 几种算法结果比较 对卡簧图像分别采用Harris算法、CSS算法以及本文算法进行角点提取。为了使结果更有可比性,CSS算法与本文算法均基于预处理得到的同一轮廓图。Harris算法由于其原理必要性只能基于原始灰度图进行。(说明:限位边框的存在,增加了背景的复杂程度。4.1节中本文算法在此类情况下已经得到有效验证。出于对比,使用无限位边框的原始图片,主要降低Harris算法检测到的冗余角点数),结果如图10。 可见,由于设备长期运行于工业现场,细小杂质不可避免,采用基于灰度的角点检测方法,如图10(b),结果显示,目标角点完全被大量杂质角点所淹没。即使考虑从中将其筛选,由于杂质角点的繁乱无序,将难以进行。 图10(c)中,CSS检测算法,在轮廓跟踪时设法丢弃了孤立杂质点轮廓,检测出的伪角点数量大大减小。但若杂质沾染在工件上,形成共同的轮廓,仍会在曲率极大值处产生伪角点,如图10(e)中U区域。 图10(f),本文方法锁定角点搜索区域,故不会对区域以外再进行检测,避免了图10(e)中伪角点簇U的产生。定位A点时,由于在L1中选择θi的局域极小值,则图10(e)T区域角点里只有一个会入选,之后根据先验信息得知T区域角点与C角点距离不在允许范围内,故被剔除。检测B点时按图10(e)箭头所示方向,定位到符合条件的角点B后,程序停止,避免了将T区域的角点误判为B。 图10 三种算法角点检测结果Fig.10 Results of corner detection by three algorithms 三种方法处理时间对比,如表2。 说明:Harris角点检测采用5×5的高斯滤波模板,CSS算法曲率尺度设为7。三种方法均在VC++环境中实现。原始图片大小为2 048 pixels×1 536 pixels。 可见,两种基于轮廓的角点提取方法,用时明显少于基于灰度信息的Harris算法。在预处理得到轮廓后,本文方法较之CSS算法,检测范围缩小,并且避免了二阶导数的求解,速度更快。 表2 三种角点检测算法时间对比Table 2 Time comparison list of three algorithms ms 对微小型工件自动化视觉测量过程中角点的定位进行了研究,提出一种基于先验信息的角点检测方法。多次利用先验信息锁定角点提取范围,降低情况复杂度,减少时间消耗。针对不同类型的角点运用不同判别方法,算法局部适应性更强。角点分批次提取,循环渐近;各批角点的提取,又由粗到精,渐近优化,及时剔除伪角点。卡簧角点检测实验表明,本方法对于目标角点定位准确、重复性高、速度快。不同位姿多次测量结果稳定在一个像素以内,整机设备连续检测2 000件卡簧工件时,由于角点定位不准造成的误判率小于1%,速度达到90件/min。可见,算法能适应时变复杂背景中多位姿工件的快速角点定位。 参考文献: [1] 于合龙,苏恒强,汪岩,等. SUSAN角点检测和匹配算法在高温变形测量中的应用 [J]. 航空学报,2013,34(5):1064-1072. YU Helong,SU Hengqiang,WANG Yan,et al. Application of SUSAN Corner Detection and Matching Algorithm in HighTemperature Deformation Measurement [J]. Acta Aeronautica et Astronautica Sinica,2013,34(5):1064-1072. [2] 张金林,曹鹏,芮挺,等. 基于二维EMD的Harris角点检测算法 [J]. 光电工程,2012,39(7):38-42. ZHANG Jinlin,CAO Peng,RUI Ting,et al. Harris Corner Detection Algorithm Based on Two-dimensional EMD [J]. Opto-Electronic Engineering,2012,39(7):38-42. [3] ZHANG Xiaohong,WANG Hongxin,Smith Andrew W B,et al. Corner Detection based on Gradient Correlation Matrices of Planar Curves [J]. Pattern Recognition(S0031-3203),2010,43(4):1207-1223. [4] Awrangjeb M,LU Guojun. Robust Image Corner Detection based on the Chord-to-Point Distance Accumulation Technique [J]. IEEE Transactions on Multimedia(S1520-9210),2008,10(6):1059-1072. [5] 曾接贤,李炜烨. 曲率尺度空间与链码方向统计的角点检测 [J]. 中国图象图形学报,2014,19(2):234-242. ZENG Jiexian,LI Weiye. Corner Detection based on Curvature Scale Space and Chain Code Direction Statistics [J]. Journal of Image and Graphics,2014,19(2):234-242. [6] 栗琳,王仲,蔡振兴,等. 基于目标轮廓的附着物定位与剔除方法 [J]. 光电工程,2012,39(5):45-51. LI Lin,WANG Zhong,CAI Zhenxing,et al. A Method of Location and Elimination of Foreign Matters Based on Navigation Contour [J]. Opto-Electronic Engineering,2012,39(5):45-51. [7] 王仲,郑镕浩,刘文静,等. 基于先验知识的微型零件检测中异物伪信息的剔除 [J]. 计算机应用,2014,34(5):1458-1462. WANG Zhong,ZHENG Ronghao,LIU Wenjing,et al. Culling of Foreign Matter Fake Information in Detection of Subminiature Accessory based on Prior Knowledge [J]. Journal of Computer Applications,2014,34(5):1458-1462. [8]求是科技. Visual C++数字图像处理典型算法及实现 [M]. 北京:人民邮电出版社,2006:406-415. [9] Rosenfeld A,Johnston E. Angle Detection on Digital Curves [J]. IEEE Transactions on Computers(S0018-9340),1973,22(9):875-878. [10] CHIN R T,THE C H. On the Detection of Dominant Points on Digital Curves [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence(S0162-8828),1989,11(8):859-872. [11] 王万良,金亦挺,赵燕伟,等. 点到弦距离累加的自适应角点检测 [J]. 中国图象图形学报,2012,17(12):1500-1508. WANG Wanliang,JIN Yiting,ZHAO Yanwei,et al. Adaptive Corner Detection based on Chord-to-Point Distance Accumulation [J]. Journal of Image and Graphics,2012,17(12):1500-1508. [12] Chetverikov D. A Simple and Efficient Algorithm for Detection of High Curvature Points in Planar Curves [C]// 10th International Conference on Computer Analysis of Images and Patterns, University of Groningen,Netherlands,August 25-27. Berlin,Germany:Springer-Verlag,2003:746-753. A Method of Symptotic Corner Detection Based on Prior Information WANG Zhong,LIU Wenjing,FU Luhua,GUO Youwei Abstract:A step-by-step asymptotic method of image corner detection is proposed in high speed vision detection for quantities of micro two-dimensional workpieces. In this method, the inherent geometric relationship in the single pixel contour is taken as a priori information, based on which, the region where corners exist is separated from full contour. After that, we select suitable algorithm to detect corners and get their positions accurately along with false corners being eliminated in time. Then, we can lock region again ... This process continues circularly, until all the corners have been detected. Experimental results show that, for the same workpiece, whose images are getting in different position and attitude, the standard deviation of distance between points is within 0.5 pixels. Compared with Harris corner detection algorithm and CSS corner detection algorithm, the proposed method is scarcely affected by foreign substance in the field. Due to the accuracy, high speed and high repeatability, this method has obvious advantage in high speed vision detection for quantities of micro two-dimensional workpieces. Key words:corner detection; prior information; quantities of micro workpieces inspection; machine vision 作者简介:王仲(1953-),男(汉族),天津人。教授,硕士,研究方向:机器视觉检测。E-mail: wangzhong@tju.edu.cn。 基金项目:国家重大科学仪器设备开发专项(2013YQ17053903) 收稿日期:2015-01-26; 收到修改稿日期:2015-04-19 文章编号:1003-501X(2016)01-0006-07 中图分类号:TP391.4 文献标志码:A doi:10.3969/j.issn.1003-501X.2016.01.002
2 在局域序列中检测角点


3 角点位置的优化


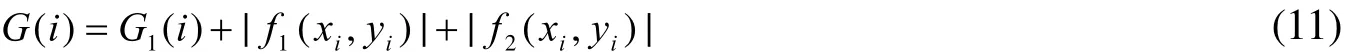
4 实验结果与分析


5 总 结
( State Key Laboratory of Precision Measuring Technology and Instruments, Tianjin University, Tianjin 300072, China )
