高碾压混凝土拱坝温控可靠性分析

裴 亮，代 萍，何 坤，吴震宇，陈建康（1.四川大学水力学与山区河流开发保护国家重点实验室，四川成都 610065；2.四川大学水利水电学院，四川成都 610065；.四川电力职业技术学院，四川成都 610072）



高碾压混凝土拱坝温控可靠性分析

裴 亮1，2，代 萍3，何 坤1，2，吴震宇1，2，陈建康1，2
（1.四川大学水力学与山区河流开发保护国家重点实验室，四川成都 610065；
2.四川大学水利水电学院，四川成都 610065；3.四川电力职业技术学院，四川成都 610072）

摘要：运用可靠度理论，考虑大气温度和关键混凝土参数的不确定性对拱坝温度场、应力场的影响，并将其作为随机变量，以控制拱坝施工期坝体最高温度为例构建坝体最高温度控制功能函数，采用响应面法解决功能函数无法显式表达的问题，从而建立拱坝施工期坝体温控失效概率和可靠度指标求解新模式。计算结果显示，与蒙特卡罗法计算结果的相对差别不超过8. 36%。新方法在解决实际工程问题时可避免大规模的数值计算，在保证计算精度的前提下大幅提高了计算效率。

关键词：高碾压混凝土拱坝；温度控制；不确定性；可靠性；响应面法

高拱坝施工过程十分复杂，受水文、气象等自然环境、施工场地及交通布置、机械设备与建筑材料、施工工艺与组织方式等诸多因素的影响，施工过程具有很强的随机性与不确定性[1-2]，这决定了大坝混凝土边界条件和自身参数的随机性，从而降低温度控制的可靠性，增大混凝土开裂的风险[3-4]，仅通过抗裂安全系数无法量化边界条件和混凝土自身参数的随机性对拱坝温度场、应力场的影响，可靠度理论为评估不确定因素影响下混凝土温控防裂效果提供了有效手段，有必要基于可靠度理论寻求一种简单、高效、精确且适用于大型实际工程的可靠度计算方法。

随着温度裂缝问题的大量出现，温度裂缝给工程带来的严重影响引起了越来越多的科技工作者的重视。20世纪90年代丁宝瑛[5]运用可靠度理论，考虑温控中设计变量的随机性，提出一种基础温差的可靠性最优化设计方法；梅明荣等[6]以混凝土嵌固板为例探讨了可靠度理论在温度应力及控制中的应用。刘宁等[7-8]视混凝土温度场、弹性模量、徐变度以及抗力等为非平稳随机过程，提出了大体积混凝土结构随机温度徐变应力首次超越可靠度的计算方法。刘有志等[9]针对大体积混凝土施工期出现的集中典型开裂风险，提出了相应温控措施。目前有关大体积混凝土施工期温控可靠性的研究成果较少，本文运用可靠度理论，考虑大气温度和关键混凝土参数的不确定性并将其作为随机变量，以控制坝体最高温度为例构建坝体最高温度控制功能函数，采用响应面法解决功能函数无法显式表达的问题，进而进行失效概率和可靠度指标求解，并与蒙特卡罗法（Monte-Carlo method）的结果进行对比以验证其求解精度。

1 温控可靠性分析方法

1. 1 结构的极限状态与失效概率

《工程结构可靠度设计统一标准》[10]对结构极限状态的定义为：整个结构或者结构的一部分超过某一特定状态就不能满足设计规定的某一功能要求，此特定状态为该功能的极限状态。结构可靠度分析中，结构的极限状态一般由功能函数加以描述。如果用x1、x2、…、xn表示结构基本随机变量，用Z＝g（x1，x2，…，xn）表示结构的功能函数，则结构的工作状态可用下式表示[11]：

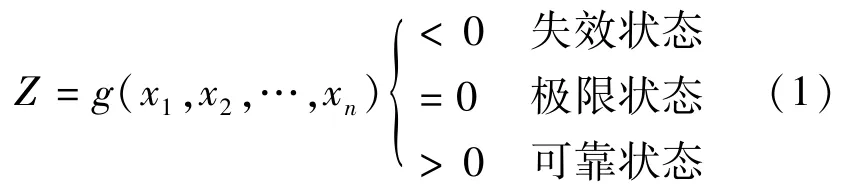
结构可靠性是用可靠度来度量的，结构可靠度定义为在规定的时间内和规定的条件下结构完成预定功能的概率，表示为Ps。结构的可靠与失效为两个互不相容的事件，因此，结构的可靠概率Ps与失效概率Pf是互补的，即

（3）式中xi为荷载和抗力基本随机变量。但是功能函数中随机变量较多或函数为非线性时，上述计算变得十分复杂，甚至难以求解。因此在实际应用时往往先求得结构可靠度指标，然后再求解相应的失效概率[11]。根据SL314—2004《碾压混凝土坝设计规范》[12]和SL282—2003《混凝土拱坝设计规范》[13]之要求，碾压混凝土拱坝的坝体温度应从基础温差、上下层温差、坝体最高温度和最大内外温差等几方面进行控制。本文以控制拱坝坝体最高温度为例，研究拱坝温度控制可靠度计算方法。

1. 2 随机变量及统计特征

影响施工期混凝土坝温度场变化的主要因素有混凝土绝热温升、混凝土热力学参数（热导率λ、热扩散率a和比热容c等）、初始条件（浇筑温度等）、边界条件和上下层混凝土温度等。在实际施工过程中，上述影响因素均存在一定的不确定性，从而影响拱坝施工期温度控制的效果。重要工程中一般都要对绝热温升和热力学参数进行试验，配合比一定的情况下绝热温升变化较小。浇筑温度的不确定性可由大气温度不确定性表示，即自然入仓情况下浇筑温度取决于大气温度和太阳辐射强度。

λ、a、c和密度ρ之间存在如式（4）所示的关系，任意一个参数可由其他参数得到：

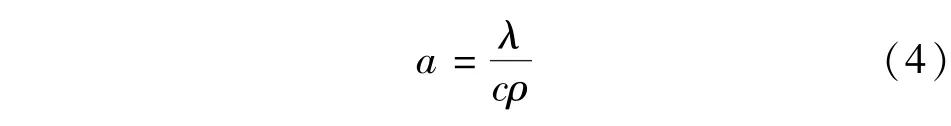
由于混凝土密度变异性较小，故选择数量级较为接近的热扩散率和比热容作为随机变量。参考设计值和其他已建和在建类似工程确定热力学参数分布特征，大气温度统计特征根据坝址区统计资料确定。国内部分碾压混凝土坝热力学参数统计如表1～3所示。

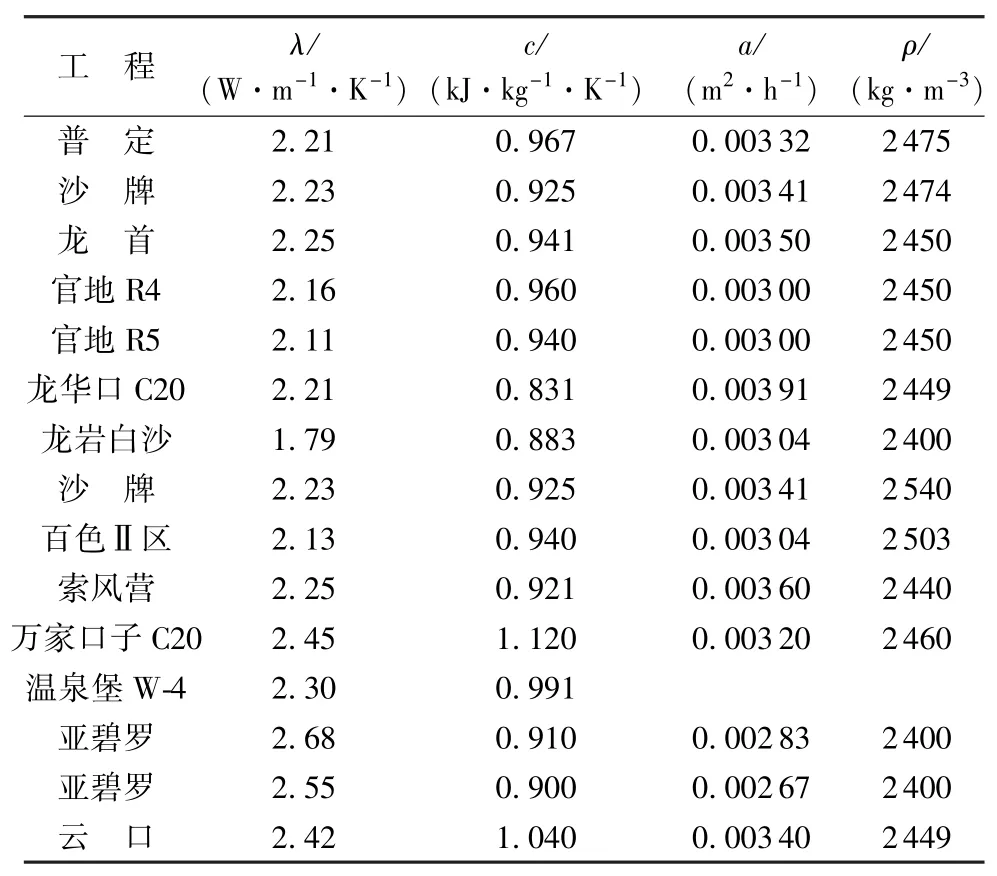
表1 国内部分碾压混凝土坝热力学参数（二级配）

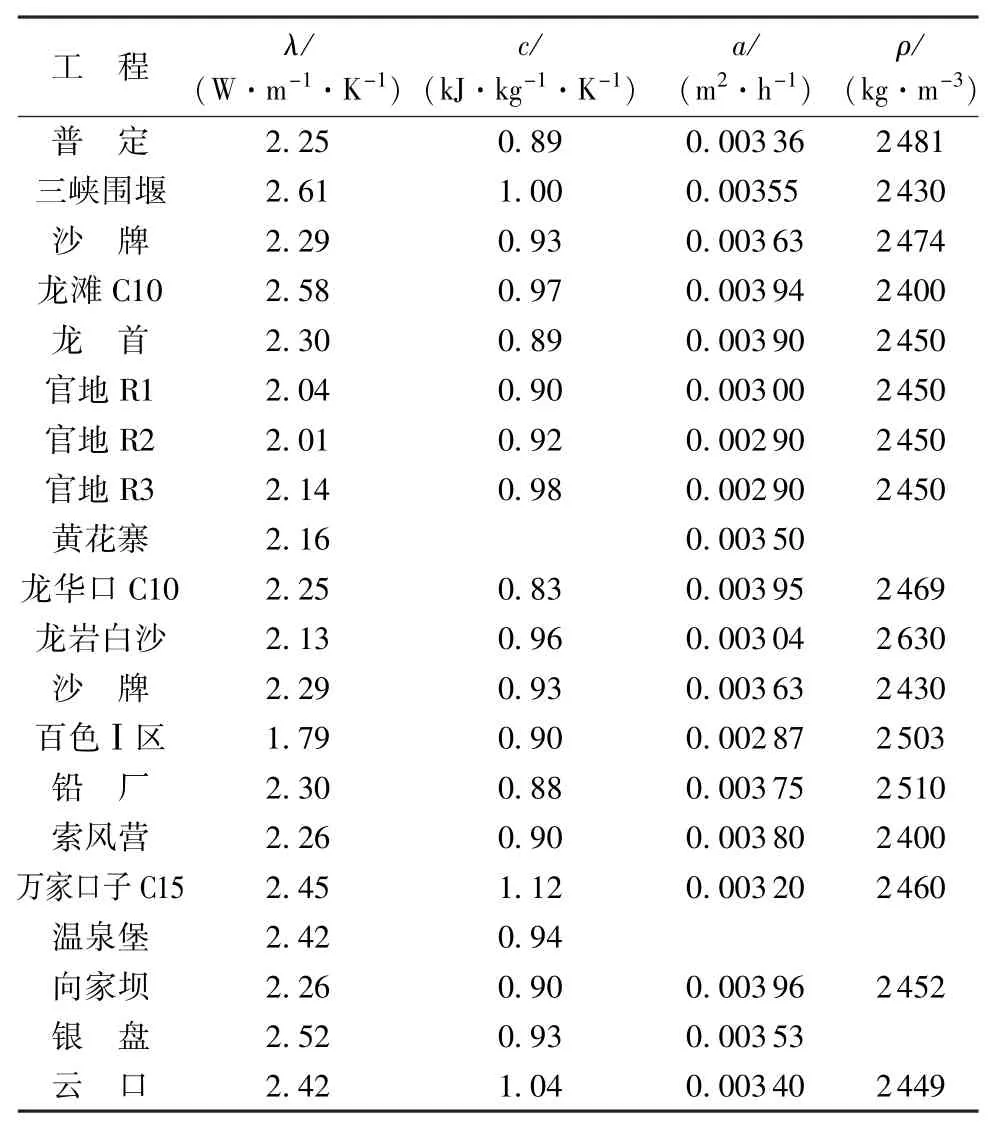
表2 国内部分碾压混凝土坝热力学参数（三级配）

1. 3 功能函数构建和失效概率求解

大坝混凝土碾压完成后即在水化热作用下开始温升，设混凝土在第1天完成碾压，第n天达到最高温度Tmax，则第1天到第n天的大气温度会对Tmax产生明显影响，且离混凝土表面越近，受到大气温度的影响越大。以1～n天的日平均温度Ti（i＝1，2，…，n）作为随机变量，则Tmax可表示为

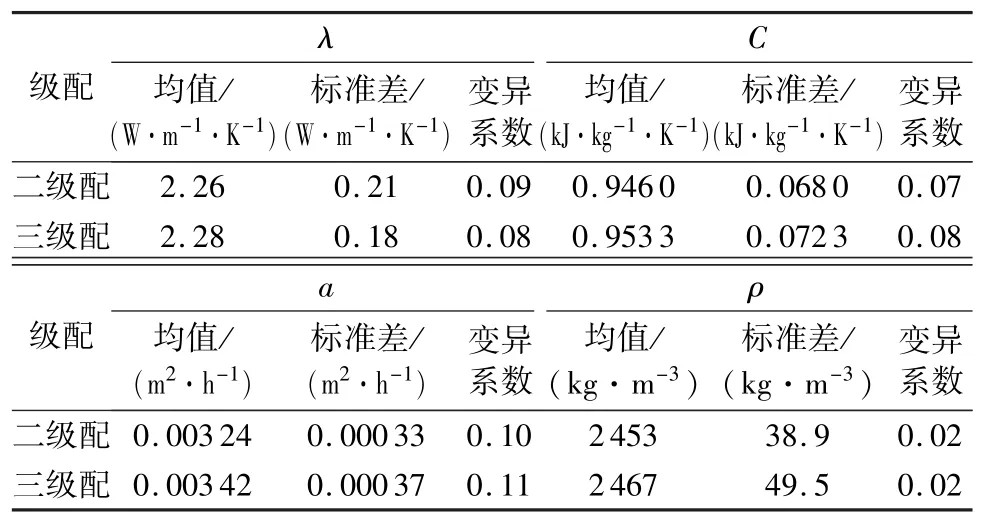
表3 国内部分碾压混凝土坝热力学参数统计

以拱坝坝体特定位置的Tmax作为荷载，以该部位最高允许温度T为抗力构建温度控制功能函数：

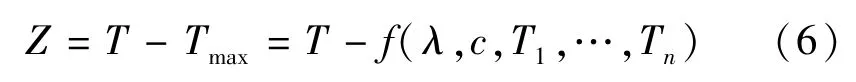
针对Tmax是关于随机变量的隐函数，不易显式表达的问题，可采用响应面法构建Tmax的响应面方程：式中a0、bi和ci为响应面函数中的待定系数。

采用Taguchi正交设计试验方法，根据正交性从全面试验中挑选出部分有代表性的点进行试验，即均匀、分散挑选若干个自变量进行数值试验。对设计的数值试验点和对应的功能函数值进行回归分析可确定式（7）中的待定系数。Tmax的响应面函数确定之后，功能函数即可被显式表达，可采用蒙特卡罗法计算温度控制的失效概率，具体步骤如下：第1步，确定随机变量及统计特征；第2步，建立功能函数；第3步，对随机变量进行数值试验；第4步，构建功能函数的响应面方程；第5步，求解失效概率和可靠度指标。

2 计算精度验证

2. 1 计算模型

设计尺寸为15 m×9 m×6 m的碾压混凝土试块，在铅直方向上将试块剖分为30 cm厚的单元，按照碾压混凝土拱坝施工工序模拟试块的浇筑。采用六面体实体热力学单元将试块离散为300个单元，共504个节点，试块有限元模型及特征点选取如图1和图2所示。

2. 2 计算参数与边界条件

试块混凝土热力学参数采用表3统计值，日平均气温采用四川省凉山州木里县气象站1997—2006年统计值，见表4。试块碾压后通水冷却，允许最高温度取29℃。试块浇筑安排见表5。

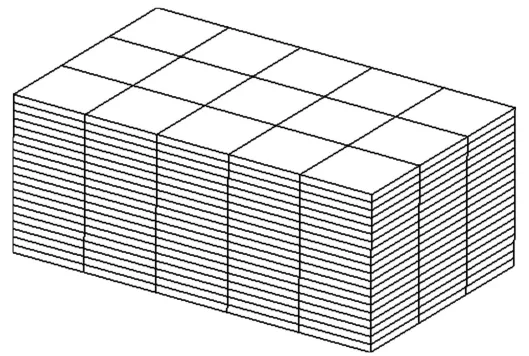
图1 试块三维有限元模型

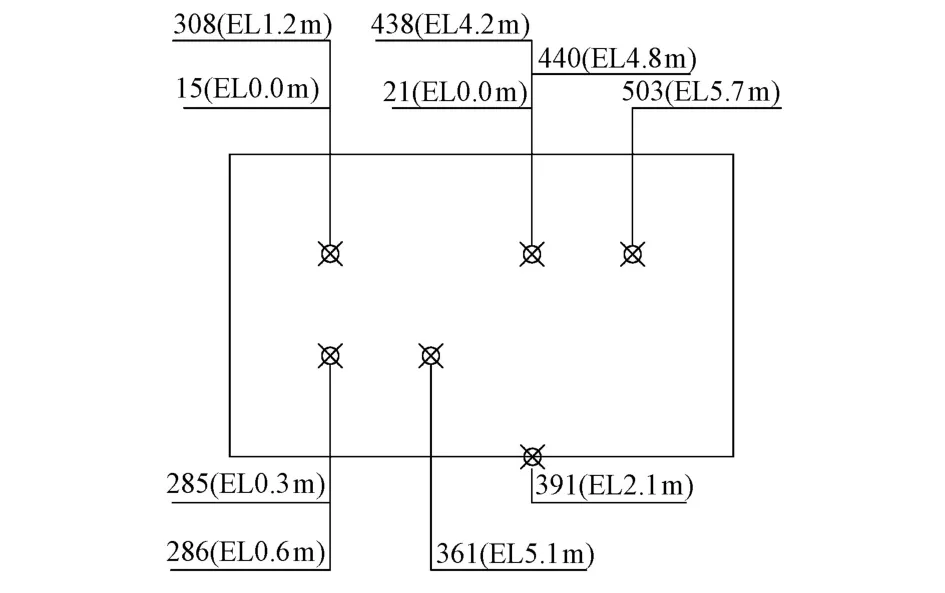
图2 特征点位置、编号及高程示意图

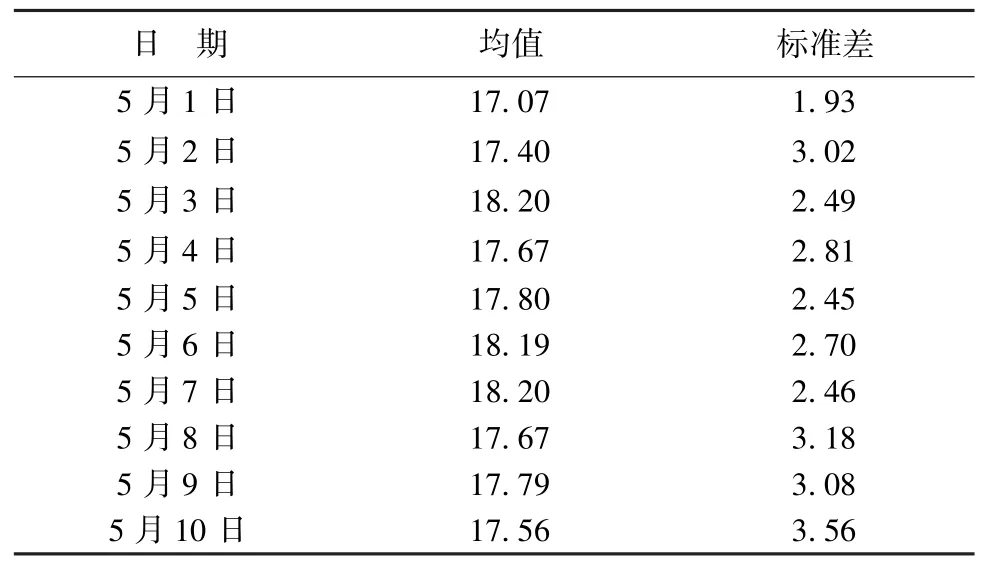
表4 四川省凉山州木里县气温统计　　℃

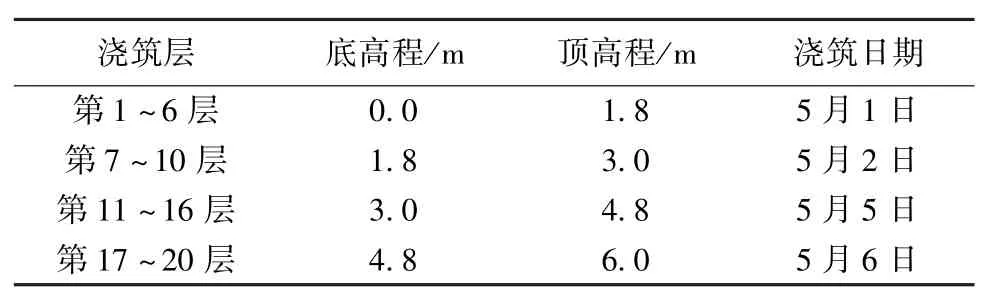
表5 混凝土试块浇筑安排

碾压混凝土试块三维温度场计算中，取侧面与顶面为散热面（第三类边界条件），底面为绝热面。考虑到试块在5月（高温季节）浇筑，碾压混凝土的浇注温度控制在16℃。

2. 3 正交数值试验

根据试块温度场三维有限元确定性分析结果可知，混凝土最高温度出现在浇筑后的第5天，因此以碾压层浇筑当天、第2天、……、第5天日平均气温T1、T2、…、T5，混凝土热导率λ和比热容c为随机变量。在试块模型中选取的特征点分别属于5月1日和5月6日浇筑的碾压层，所以对应的随机变量不同，需要对每组特征点分别进行数值试验。

以随机变量作为试验因素，每个因素取五水平按正交表L25（57）进行正交数值试验，L25（57）表示对7个试验因素，每个因素选5个水平共进行25次试验。正交试验因素水平见表6和表7，试验结果如图3和图4所示。

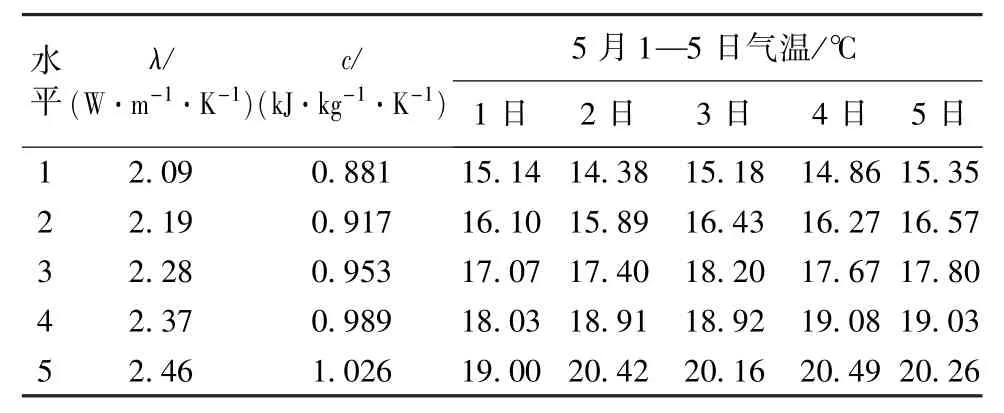
表6 因素水平表1

表7 因素水平表2

图3 各特征点正交试验结果1

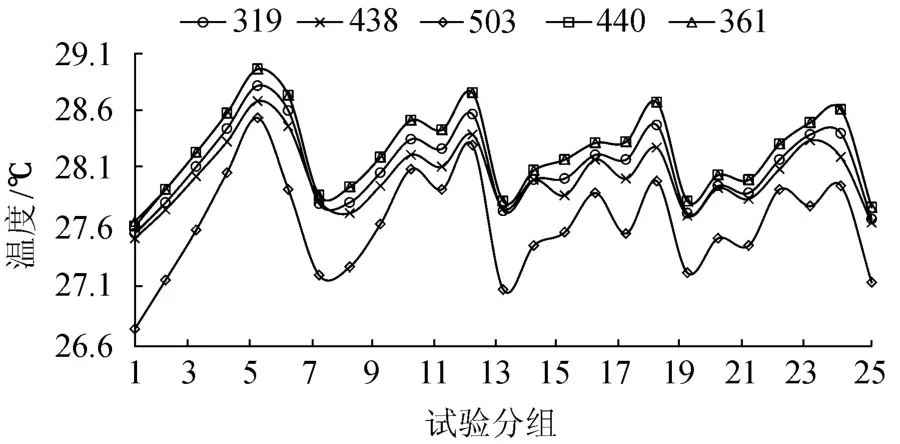
图4 各特征点正交试验结果2

根据试验结果，通过全回归建立每个特征点最高温度与随机变量的响应面方程，计算得到的各特征点回归方程相关性高，复相关系数R2和修正复相关系数R2adj均大于0. 99，所建立的响应面方程能够对试验因素和试验结果间的关系做出精确的拟合。

2. 4 失效概率、可靠度指标求解

由于试块各层的浇筑时间差异，各层内特征点的随机变量不完全相同。具有相同浇筑时间的特征点其随机变量相同，只需设计一组正交试验即可得到各点的响应面方程，进而求解各点失效概率与可靠度指标。各特征点回归方程相关性高，响应面方程均能够对试验因素和试验结果间的关系做出精确的拟合。确定性分析中试块混凝土最高温度均小于允许值，可靠性分析结果显示，在随机变量影响下，混凝土最高温度超过允许值的概率较大，即温度控制存在较大风险，可靠度指标β最大值仅2. 28，运用可靠度理论评价混凝土温控效果更加科学合理。

试块温度场仿真分析计算量小、耗时少，计算结果与蒙特卡罗法求得的精确解的对比如表8所示。由表8可知，本文提出的方法计算得到的失效概率与蒙特卡罗法计算结果最大相对偏差8. 36%，计算精度良好，可用于实际工程温控可靠性计算。

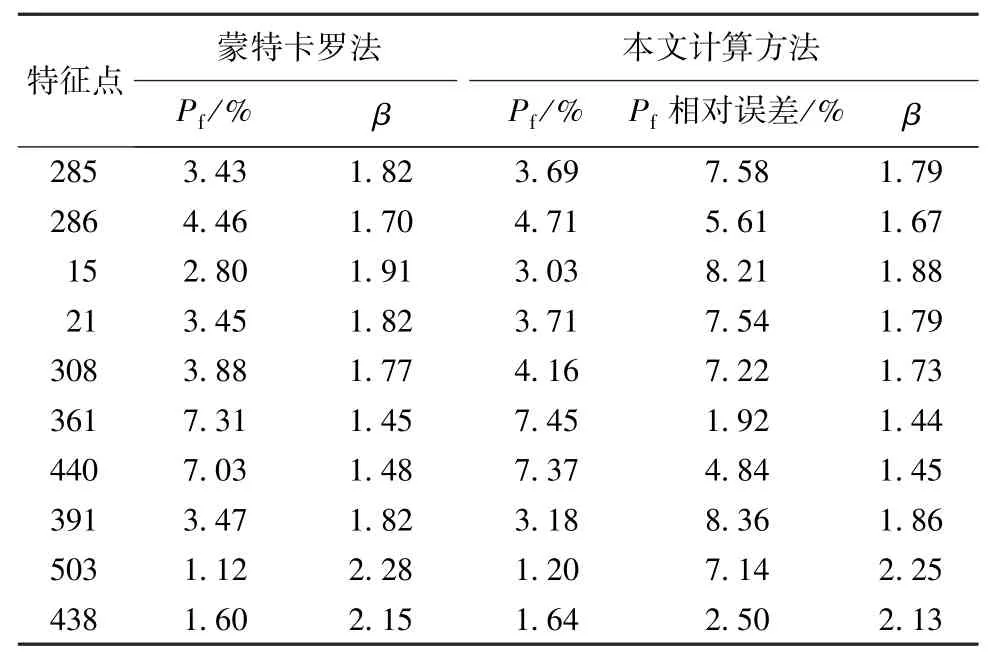
表8 失效概率和可靠度指标

3 算例分析

3. 1 工程概况

立洲水电站位于四川省凉山彝族自治州木里藏族自治县境内。电站采用混合式开发，枢纽工程由碾压混凝土双曲拱坝、坝身泄洪系统、右岸地下长引水隧洞及右岸地面发电厂房组成。正常蓄水位2088. 0 m，最大坝高128. 0m，电站装机容量355 MW（包含10 MW生态机组），多年平均发电量为15. 46亿kW·h，水库总库容1. 897亿m3。

3. 2 随机变量及功能函数

根据立洲碾压混凝土拱坝温度场仿真分析成果，选择1975 m高程强约束高温区为研究对象，计算其最高温度控制可靠性。该部位混凝土碾压时间为2012年6月12日，于2012年6月18日达到最高温度。根据本文提出的温控可靠度分析方法，选择混凝土碾压后1～7天的日平均温度Ti（i＝1，2，…，7）、热扩散率和比热容作为随机变量，按照式（7）构建温度控制功能函数。各随机变量的统计特征如表9所示。

按照表9分别对随机变量按照正交表L25（37）设计正交数值试验，根据试验结果采用不完全二次多项式构建随机变量与混凝土最高温度的响应面方程。6个特征点的响应面方程复相关系数和修正复相关系数均在0. 99以上，说明响应面方程对随机变量和混凝土最高温度间的关系能做出精确拟合。

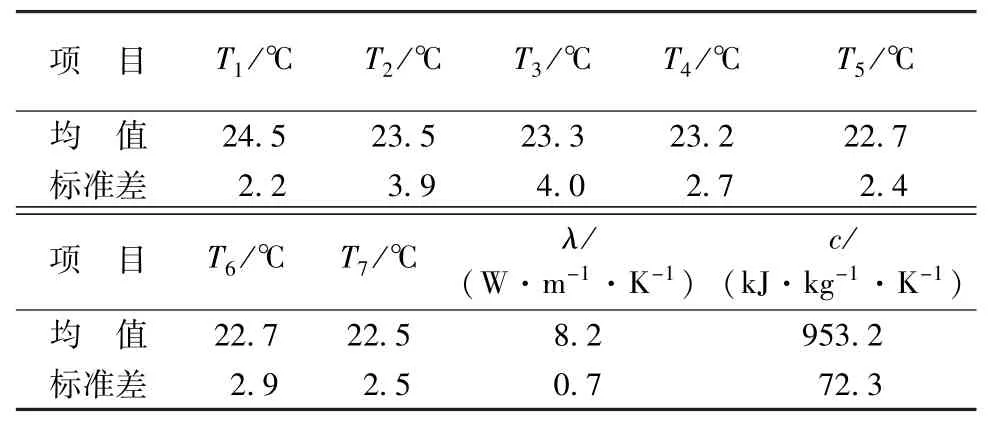
表9 随机变量及其统计特征

3. 3 失效概率与可靠度指标求解

各特征点位置如图5所示，可靠度计算成果见表10。点Y1和Y4均在上游面处，虽然其最高温度较内部低，但对大气温度变化更为敏感，在日气温波动的影响下失效概率最大，可靠度指标β为2. 73和2. 74；点Y2和Y5距离表面约4 m，受大气温度的影响小且散热条件良好，失效概率最小，β值分别为4. 08和4. 03；点Y3和Y6位于坝体内部，主要受散热条件的影响，最高温度高，失效概率较大，β值分别为3. 03和3. 06。

图5 1975 m高程特征点位置示意图

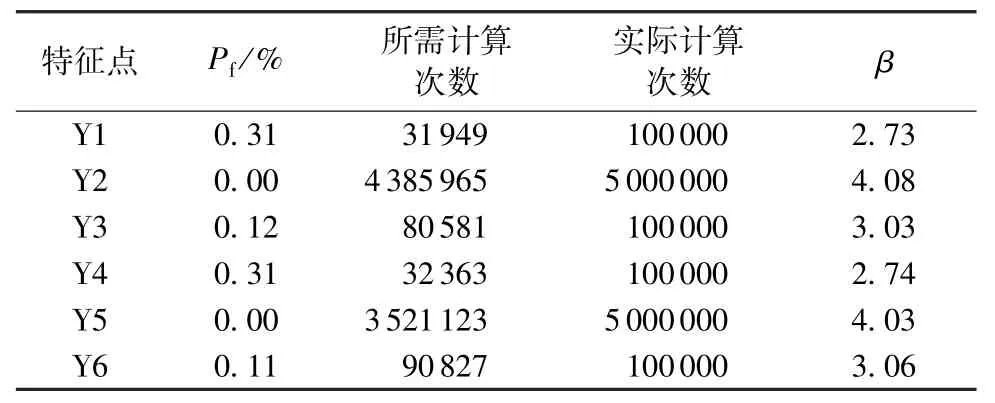
表10 失效概率与可靠度指标

4 结 语

在碾压混凝土拱坝施工过程中，热力学与边界条件参数的随机性可能导致温度控制达不到设计要求而导致裂缝出现。本文通过统计国内在建和已建碾压混凝土坝热力学参数和环境温度确定了随机变量及其统计特征，以控制碾压混凝土施工期最高温度为例构建可靠性分析功能函数。为解决实际工程中可靠性分析计算量大、耗时久的问题，通过正交试验建立了随机变量与混凝土温度的响应面方程，并将其代入功能函数进行失效概率求解，在保证计算精度的前提下大幅提高了计算效率。

本文提出的碾压混凝土拱坝混凝土温控可靠性

分析方法考虑了随机变量的统计特征，模拟相对误差在9%以内，在立洲碾压混凝土拱坝施工期温控可靠度分析中的应用表明，该方法在解决实际工程问题时可避免大规模数值计算。但边界条件的设定、随机变量的选取和量化等方面仍存在许多不妥之处，有待在今后的工作中继续深入研究。

参考文献：

[ 1 ]任炳昱.高拱坝施工实时控制理论与关键技术研究[D].天津：天津大学，2010.

[ 2 ]吴斌平.水利水电工程施工控制学[D].天津：天津大学，2013.

[ 3 ]马跃峰.基于水化度的混凝土温度与应力研究[D].南京：河海大学，2006.

[ 4 ]刘有志.水工混凝土温控和湿控防裂方法研究[D].南京：河海大学，2006.

[ 5 ]丁宝瑛.混凝土坝温度控制的可靠性最优化设计[J].水利学报，1986，17（6）：31-38.（DING Baoying. The reliability optimum design of temperature control for mass concrete dams [ J]. Journal of Hydraulic Engineering，1986，17（6）：31-38.（in Chinese））

[ 6 ]梅明荣，陈和群.混凝土嵌固板温控可靠度分析[J].河海大学学报（自然科学版），1994，22（2）：97-101.（MEI Mingrong，CHEN Hequn. Reliability analysis of temperature control for concrete fixed plate [J]. Journal of Hohai University（National Science），1994，22（2）：97-101.（in Chinese））

[ 7 ]刘宁，刘光廷.大体积混凝土结构温度场的随机有限元算法[J].清华大学学报（自然科学版），1996，36（1）：41-47.（LIU Ning，LIU Guangting. Random temperature field of mass concrete structure solved by stochastic finite element method [ J ]. Journal of Tsinghua University （Science and Technology），1996，36（1）：41-47.（in Chinese））

[ 8 ]刘宁，刘光廷.混凝土结构温度徐变应力的首次超越可靠度[J].固体力学学报，1998，19（1）：38-44.（LIU Ning，LIU Guangting. The first excursion reliability analysis of mass concrete structures influenced by random thermal creep stresses[J]. Acta Mechnica Solida Sinica，1998，19（1）：38-44.（in Chinese））

[ 9 ]刘有志，刘伟明，徐波，等.武都碾压混凝土坝施工期温控措施防裂效果分析[J].水力发电，2011，37（12）：27-30.（LIU Youzhi，LIU Weiming，XU Bo，et al. Analysis on temperature control and crack preventing in Wudu RCC Dam during construction [ J]. Water Power，2011，37 （12）：27-30.（in Chinese））

[10] GB20153—92 工程结构可靠度设计统一标准[S].

[11]赵国藩，金伟良，贡金鑫.结构可靠度理论[M].北京：中国建筑工业出版社，2000.

[12] SL314—2004 碾压混凝土坝设计规范[S].

[13] SL 282—2003 混凝土拱坝设计规范[S].

Reliability analysis of temperature control of high RCC arch dam/ /

PEI Liang1，2，DAI Ping3，HE Kun1，2，WU Zhenyu1，2，CHEN Jiankang1，2（1. State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China；2. College of Water Resource and Hydropower，Sichuan University，Chengdu 610065，China；3. Sichuan Electric Vocational and Technical College，Chengdu 610072，China）

Abstract：In order to control the maximum temperature in an arch dam during its construction period，a performance function for control of the maximum temperature in the dam body was constructed based on the reliability theory，in which the influences of randomness of the atmospheric temperature and concrete parameters on the temperature field and stress field of the arch dam were considered，and the atmospheric temperature and concrete parameters were taken as the random variables. The response surface method was used to solve the problem，in which the performance function cannot be explicitly expressed，and a new mode for solving the failure probability and reliability index of temperature control in the dam body during the construction of the arch dam was developed. The calculation results show that the error of this method is less than 8. 36%as compared with the results of the Monte Carlo method. The method allows the user to avoid large-scale numerical computation and improve the computational efficiency significantly with a high level of accuracy.

Key words：high RCC arch dam；temperature control；uncertainty；reliability；response surface method

收稿日期：（2014 11 13 编辑：郑孝宇）

作者简介：裴亮（1986—），男，讲师，博士，主要从事大体积混凝土温控防裂研究。E-mail：peiliang8649@163. com

中图分类号：TV315

文献标志码：A

文章编号：1006 7647（2016）01 0090 05