软土地基上水闸整体结构优化设计

崔朕铭，蔡 新，，黄海田，樊志远，郭兴文（.河海大学水利水电学院，江苏南京 0098；.河海大学力学与材料学院，江苏南京 0098；.江苏省水利工程质量监督中心站，江苏南京 009）



软土地基上水闸整体结构优化设计

崔朕铭1，蔡 新1，2，黄海田3，樊志远3，郭兴文2
（1.河海大学水利水电学院，江苏南京 210098；2.河海大学力学与材料学院，江苏南京 210098；
3.江苏省水利工程质量监督中心站，江苏南京 210029）

摘要：针对软土地基上水闸整体结构的优化设计问题，以江苏省苏北某水闸为例，建立了以闸室与群桩基础结构关键几何尺寸为设计变量，闸室与群桩基础总造价最低为目标函数，闸室结构抗滑稳定性、地基承载力、基底应力、闸室与桩基结构强度、闸室沉降和桩顶水平位移为约束条件的优化设计数学模型，利用ANSYS软件的优化模块进行寻优搜索，分别求得水闸整体结构优化设计方案和闸室结构优化设计方案。结果表明：水闸整体结构优化设计方案总造价比闸室结构优化设计方案总造价少2. 7%，桩顶水平位移达到限定值，优化效果更显著。

关键词：水闸；桩基；软土地基；结构设计；优化设计；有限元

水闸作为一种具有挡水和泄水功能的低水头水工建筑物，在水利工程中应用广泛，多建于河道、渠系、水库、湖泊及滨海地区。江苏省黄淮平原、江淮湖洼平原、苏北滨海平原及长江三角洲平原地区的土质具有高含水率、高孔隙比、高压缩性及低强度等特点[1]，为软土地基，往往不能满足水闸结构对地基的要求，需要进行地基处理。与岩基和硬土地基上的水闸结构设计相比，软土地基上水闸结构的设计增加了基础结构的设计，需考虑闸室和基础结构的相互影响，涉及的问题更加复杂。

水闸工程常用的地基处理技术主要有换土垫层、强夯、振动水冲、桩基础、沉井基础、深层搅拌桩等[2]。其中桩基础设计和施工技术发展成熟，实践经验较多，不仅可显著提高地基承载力，减小沉降量，减轻上部结构重量，而且适用性强，已广泛应用于各类软土地基上的水闸建设。

目前，软土地基上水闸结构的设计主要采用规范[3]规定的方法，对闸室和基础结构分开设计，闸室结构作为外荷载加到基础上，仅考虑闸室和基础结构之间力系的简化传递，未考虑结构间的相互影响与整体工作效应，因而设计出的结构方案不一定是最优方案。近年来，众多学者针对水闸结构的优化设计开展了研究，并取得了一定的成果。韩延成等[4]应用复形法对开敞式水闸进行闸室段的优化，得到更加经济的结构尺寸，降低了工程造价；黄小平等[5]建立了微分进化算法的水闸桩基优化模型，该优化模型能快速给出桩基设计各参数的最优化取值组合，达到提高设计效率、节省工程造价的目的；刘冬梅[6]在对橄榄坝闸室上部框架进行优化设计时，以框架结构的梁与柱截面尺寸为设计变量，以梁与柱的最大弯曲强度、最大剪力度及配筋率上下限为控制条件，以混凝土与钢筋的总成本为目标函数，得到比较合理的框架结构截面尺寸；刘书龙等[7]建立了水闸边墩结构优化设计数学模型，采用复合形法对边墩结构进行优化设计，优化方案经济效益明显；邹武停[8]以闸墩厚度、闸底板长度和厚度作为设计变量，以抗滑稳定条件、地基承载力和强度条件为约束条件，以总投资为目标函数，建立了开敞式水闸闸室结构优化设计的数学模型，得出了经济实用的结构尺寸。

上述已有优化研究均单独分开考虑闸室和基础结构，未涉及水闸闸室和基础整体结构的优化。本文结合江苏省软土地基上某水闸工程实例，将闸室和基础结构作为整体考虑，按照相应规范的约束条件，基于优化设计理论，对该水闸闸室和基础整体结构进行优化设计研究，提出了该水闸整体结构的最优结构形式。

1 工程结构优化设计数学模型

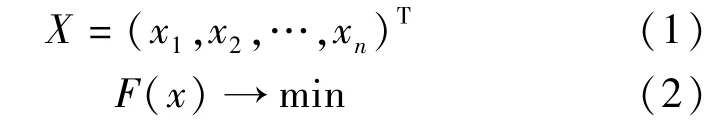
求设计变量满足约束条件

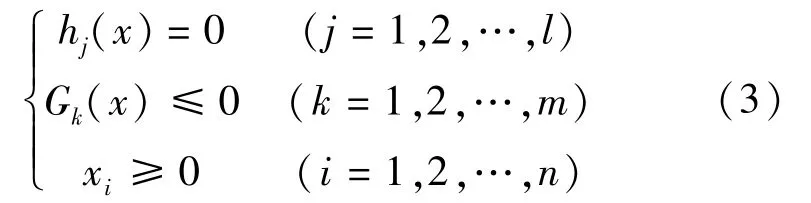
式中：xi为优化的设计变量，代表设计方案；F（x）为优化的目标函数，如造价最低，质量最轻等；hj（x）、Gk（x）为优化的约束函数，如规范规定的结构在强度、刚度、稳定性等方面的要求和限制；n为设计变量个数；l为等式约束的个数；m为不等式约束的个数。工程结构的优化设计问题一般都是有约束的非线性规划问题[9]。

2 水闸整体结构优化设计工程实例

2. 1 工程背景

江苏苏北某水闸工程闸室总净宽为20. 0 m，共2孔，单孔净宽10. 0 m，采用钢筋混凝土结构，两孔一联整体式底板。闸室底板顶面高程-2. 00 m，底板厚1. 5 m，顺水流方向长度为16 m，中墩厚1. 2 m，边墩厚1. 0 m，闸室总宽度23. 2 m。闸室采用钻孔灌注桩基础，桩径120. 0 cm，桩顶高程-3. 50 m，桩底高程-21. 50m，桩长18. 0m，共30根。闸室为开敞式，采用闸门结合胸墙挡水。胸墙采用钢筋混凝土板梁结构，底高程2. 50 m，顶高程5. 50 m，闸顶高程与海堤等高，为7. 50 m。

2. 2 水闸整体结构优化设计数学模型

根据该水闸结构特征，结合规范规程及安全经济的设计要求，建立其整体结构优化设计数学模型。

2. 2. 1 设计变量

根据闸室的结构特点及影响闸室受力和稳定的主要因素，同时考虑闸室和基础相互作用机理[10]，选取底板厚度（x1）、中墩厚度（x2）、边墩厚度（x3）、桩径（x4）等关键几何尺寸为设计变量，如图1所示；而底板长度与闸室防渗要求及上部结构布置有关，底板宽度由水力计算确定，桩基长度由桩端所处持力层确定，因此定为不变参数。同时，考虑到计算模型的复杂性，假定桩基排列情况和桩间距不变。

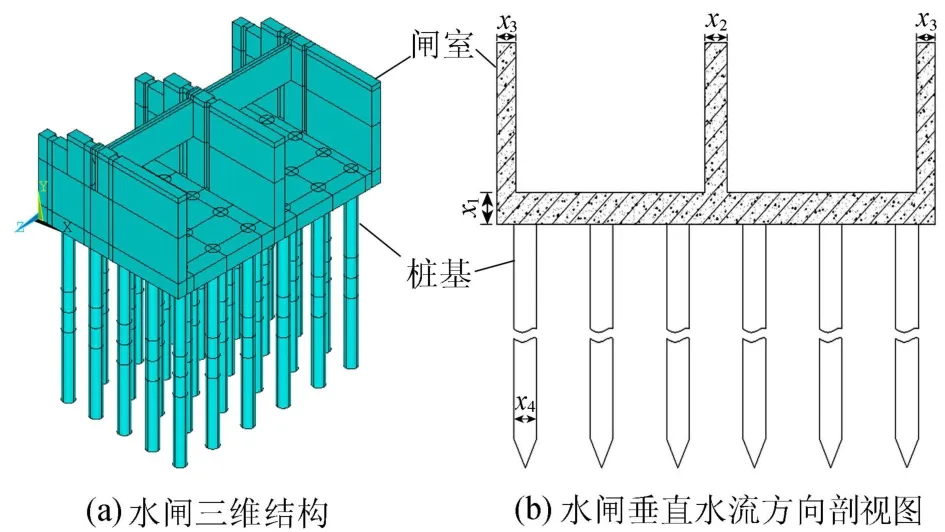
图1 水闸整体结构示意图（单位：m）

2. 2. 2 目标函数

目标函数是判别设计方案优劣的数学表达式，是设计变量的函数。工程结构优化问题一般选取造价最低、结构总体积最小等作为优化目标。水闸工程结构的造价主要取决于其总混凝土方量，还与施工等环节有关。本文选取水闸整体结构的总造价最低为目标函数，其中各部分钢筋混凝土结构造价按综合单价计算，计算公式为式中：pi为水闸各部分结构材料综合单价；Vi为水闸各部分结构的体积。

2. 2. 3 约束条件

约束条件是有关规范规程及施工、构造等方面的限制条件，一般包括几何和性态等方面的要求，这里性态约束包括地基承载力约束、基底应力约束、抗滑稳定约束、闸室结构强度约束、桩基结构强度约束、闸室沉降约束、桩顶水平位移约束。

a.几何约束。根据SL265—2001《水闸设计规范》[3]的限定，底板厚度取闸孔净宽的1/6～1/8，闸墩厚度需满足构造要求，其范围由闸墩在门槽缩颈处的最小厚度限定值确定。根据该水闸结构特点确定其几何约束为底板厚度大于1. 25m，小于1.68m；中墩厚度大于1.00 m，小于1.20 m；边墩厚度大于0.70 m，小于1. 00 m；桩基桩径大于0. 80 m，小于1. 20 m。

b.地基承载力约束。闸室平均基底应力-σb不大于地基允许承载力，即71. 20 kPa；最大基底应力σmax不大于地基允许承载力的1. 2倍，即85. 44 kPa；闸室基底压力的最大值和最小值之比不大于规范[3]规定的允许值，即基本组合荷载工况下不超过1. 50，特殊组合荷载工况下不超过2. 00。

c.抗滑稳定约束。闸室的抗滑稳定安全系数Kc不小于规范[3]规定的允许值，即基本组合荷载工况下不低于1. 35，特殊组合荷载工况下不低于1. 20。

d.闸室和桩基结构强度约束。闸室结构采用C30钢筋混凝土，桩基采用C25混凝土，C30混凝土的抗拉强度标准值为2. 0 MPa，轴心抗压强度标准值为20 MPa；C25混凝土的抗拉强度标准值为1. 75 MPa，轴心抗压强度标准值为17 MPa[11]。强度约束条件控制闸室内压应力σpps不超过轴心抗压强度标准值20 MPa，桩基内压应力σpps不超过17 MPa，考虑截面配筋作用，根据一般的实际工程经验，闸室和桩基钢筋混凝土结构的最大拉应力σsts和σpts应不超过4 MPa[9]。

e.闸室沉降。闸室最大沉降值smax不得超过规范[3]规定的允许值15 cm，最大沉降差不超过5 cm。

f.桩顶水平位移约束。根据GB 50007—2011《建筑地基基础设计规范》[12]，灌注桩桩顶水平位移值sp不超过0. 5 cm。

2. 3 结构计算模型

结构分析借助商用软件ANSYS，编写了基于APDL语言的水闸整体结构优化计算命令流，实现了参数化建模[13]，整体结构和地基的计算模型如图2所示，闸室与群桩结构的计算模型如图3所示。单元总数为169950个，总节点数215566，其中闸室结构单元数为17 417个，桩基结构单元数为6 480个。考虑到消除边界效应，模型的选取范围从闸室向左右岸及上下游各延伸2倍闸室宽度，即46. 4m，地基深度取为2倍桩基长度，即36 m。坐标原点取在底板与右岸边墩相交处的上游底部，x轴正向为顺河流方向，从上游指向下游；y轴正向铅直向上；z轴正向由左岸指向右岸。计算中模型底部采用固端约束，x、z方向两侧边界为法向约束，顶部自由。

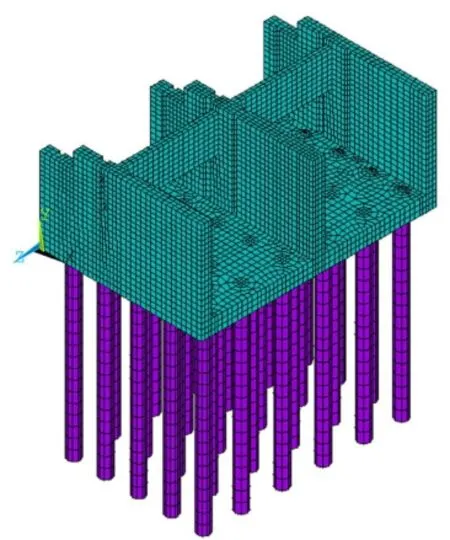
图3 闸室结构与桩基结构计算模型

闸室下地基土层大致为6层，闸室与桩基结构混凝土材料采用线弹性本构模型[14]模拟，考虑到软土地基的性质以及闸底板与土体、桩土相互作用的工作特点，土体采用D-P本构模型模拟，桩土接触、底板土体接触采用基于摩尔库伦摩擦特性的非线性本构模型模拟。土体参数如表1所示，土层自上而下编号，闸室与桩基结构材料参数如表2所示。

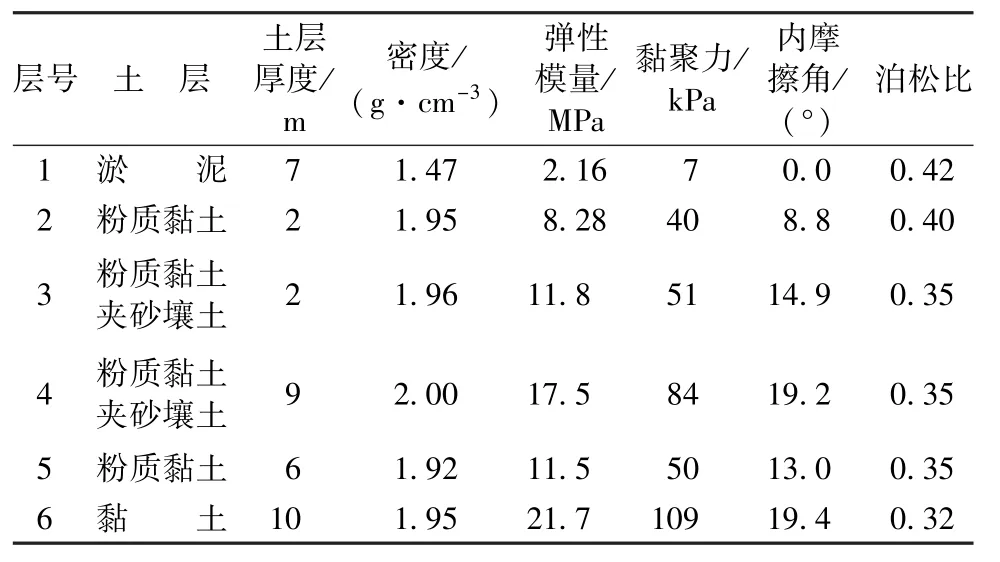
表1 土体参数

表2 闸室与桩基结构材料参数

完建期、设计蓄水位、校核蓄水位、设计挡潮水位、校核挡潮水位5种工况的上下游水位如表3所示。

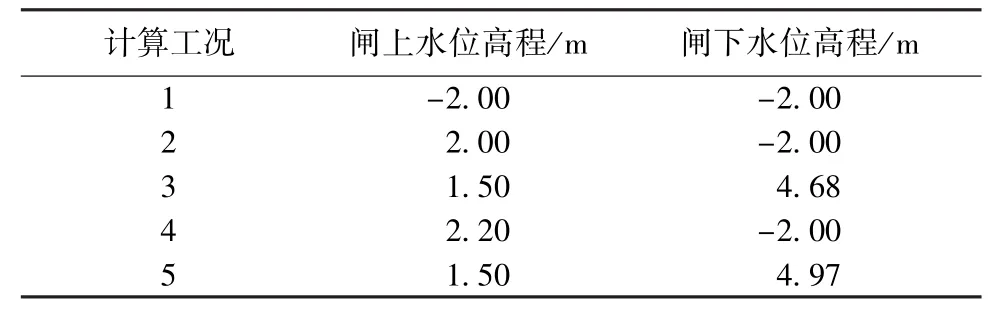
表3 计算工况

2. 4 优化设计结果及分析

利用ANSYS的APDL参数化语言和优化求解器，通过参数化建模对所建立的优化数学模型进行可行域内的寻优搜索，优化设计计算结果如表4所示。

由表4可知：与原设计方案相比，两种优化方案设计变量和总造价均有所减小，其中水闸整体结构优化设计方案总造价比闸室结构优化设计方案总造价少2. 7%，优化效果更显著。如图4所示，经过优化设计后，桩顶水平位移在工况4下达到临界约束，

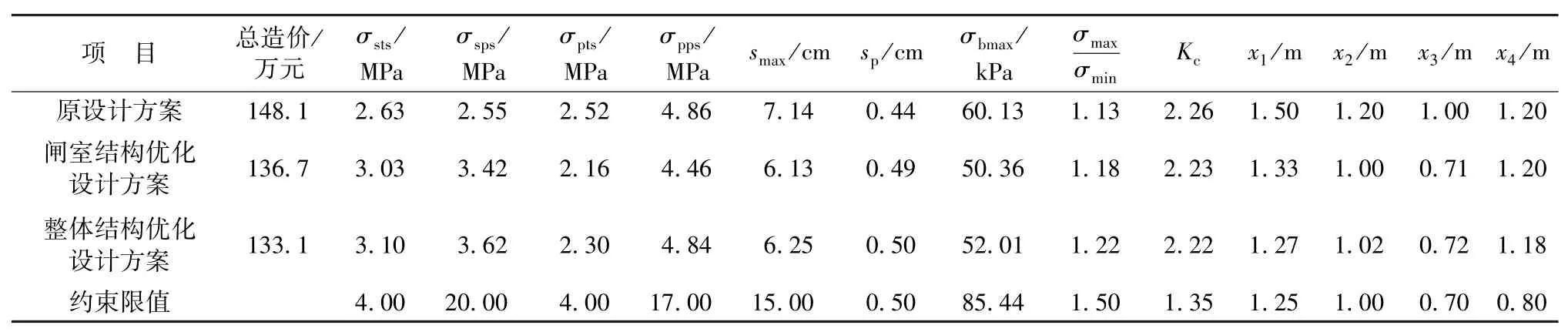
表4 水闸结构优化设计结果

闸室应力有较大幅度增大，群桩结构应力有所减小，并且都在混凝土抗压强度和钢筋混凝土抗拉强度范围内，整体受力更为均匀合理，基底压应力和闸室沉降有所减小，水闸结构的受力和变形状态有所改善，强度、刚度、稳定性均满足规范要求，表明水闸整体结构优化设计方案是安全可靠、经济合理的。相比传统的设计方法，将闸室和基础作为整体设计，能更加真实地反映水闸结构的整体工作性态，充分利用闸室和基础的结构抗力，得到更经济合理的水闸结构尺寸，可为软土地基上水闸结构设计提供依据。

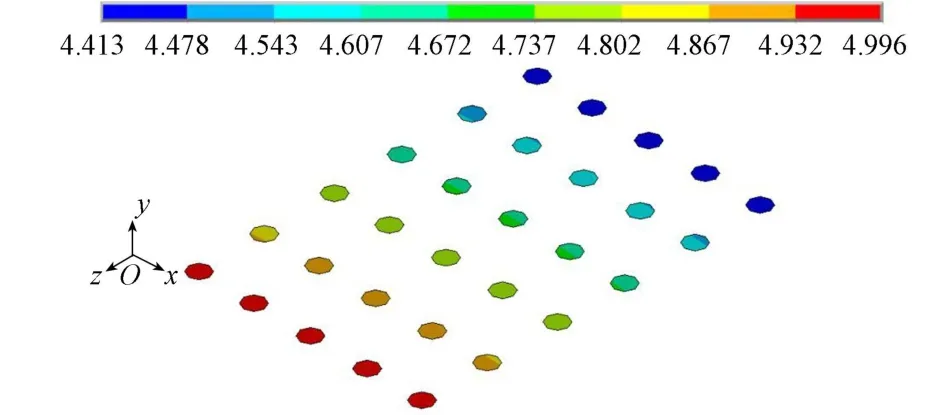
图4 优化后工况4下桩顶水平位移云图（单位：mm）

3 结 论

a.运用优化设计理论，在满足水闸结构几何约束和性态约束的条件下，对水闸整体结构进行优化设计是可行和有效的。

b.优化后水闸工程总造价较原设计方案有较大幅度的减小，整体受力更为均匀合理，闸室位移和基底压应力有所改善，抗滑稳定和结构强度均满足规范要求，表明优化设计方案安全可靠、经济合理。

c.将闸室和基础结构作为整体设计，更真实地反映了闸室和基础结构的相互作用及整体工作性态，从而得到更为经济合理的结构设计方案。

参考文献：

[ 1 ]陈锡林，沈长松.江苏水闸工程技术[M].北京：中国水利水电出版社，2013：342.

[ 2 ]张世儒，陈宝华.水闸[M].北京：中国水利水电出版社，2003：218.

[ 3 ] SL265—2001 水闸设计规范[S].

[ 4 ]韩延成，徐云修.开敞式水闸闸室段结构优化[J].中国农村水利水电，2000（4）：34-37.（HAN Yancheng，XU Yunxiu. The optimization design of open sluice chamber structure[J]. China Rural Water and Hydropower，2000 （4）：34-37.（in Chinese））

[ 5 ]黄小平，张梁，平扬.微分进化算法在软土水闸桩基优化设计中的应用[J].中国农村水利水电，2013（5）：115-117.（HUANG Xiaoping，ZHANG Liang，PING Yang. Application of differential evolutionary algorithm in optimization design of sluice pile foundation on soft soil [J]. China Rural Water and Hydropower，2013（5）：115-117.（in Chinese））

[ 6 ]刘冬梅.闸室结构静动力分析及上部框架优化设计[D].南京：河海大学，2006.

[ 7 ]刘书龙，卢光春，周储伟，等.大跨度水闸边墩优化及可靠度分析[J].河海大学学报（自然科学版），1997，25 （4）：67-72.（LIU Shulong，LU Guangchun，ZHOU Chuwei，et al. Optimal design and reliability analysis of large span sluice pier [J]. Journal of Hohai University （National Science），1997，25（4）：67-72.（in Chinese））

[ 8 ]邹武停.开敞式水闸闸室结构优化设计[D].杨凌：西北农林科技大学，2012.

[ 9 ]蔡新，李洪煊，武颖利，等.水下隧道结构优化设计[J].河海大学学报（自然科学版），2009，37（6）：665-668. （CAI Xin，LI Hongxuan，WU Yinli，et al. Optimal design of structure of underwater tunnels[J]. Journal of Hohai University（Natural Sciences），2009，37（6）：665-668.（in Chinese））

[10]宋晓，黎鹏，徐光胜.大型群桩-软土共同作用性状研究[J].河南大学学报（自然科学版），2010，40（2）：207-212.（SONG Xiao，LI Peng，XU Guangsheng. The analysis of behavior of large pile groups-Soil interaction [ J]. Journal of Henan University（Natural Sciences），2010，40 （2）：207-212.（in Chinese））

[11] SL191—2008 水工混凝土结构设计规范[S].

[12] GB50007—2011 建筑地基基础设计规范[S].

[13]李芬花，马慧，卢东海，等. ANSYS零阶方法和一阶方法的重力坝断面优化研究[J].水利水电技术. 2014，45 （1）：69-72.（LI Fenhua，MA Hui，LU Donghai，et al. Research on section optimization of gravity dam with ANSYS based zero-order and first-order methods [ J]. Water Resources and Hydropower Engineering，2014，45 （1）：69-72.（in Chinese））

[14]詹青文，吴盖.跃洲水电站泄水闸结构稳定分析[J].水电能源科学，2011，29（9）：103-106.（ZHAN Qingwen，WU Gai. Stability analysis of sluice in Yuezhou hydropower station [ J]. Water Resources and Power. 2011，29（9）：103-106.（in Chinese））

Optimal design of overall sluice structure on soft foundation/ /

CUI Zhenming1，CAI Xin1，2，HUANG Haitian3，FAN Zhiyuan3，GUO Xingwen2（1. College of Water Conservancy and Hydropower Engineering，Hohai University，Nanjing 210098，China；2. College of Mechanics and Materials，Hohai University，Nanjing 210098，China；3. Hydraulic Engineering Quality Supervision Station of Jiangsu Province，Nanjing 210029，China）

Abstract：The optimal design of an overall sluice structure on a soft foundation was studied，with a sluice in North Jiangsu Province as a case study. A mathematical model for the optimal design of the sluice was established，in which the key geometrical parameters for the sluice chamber and pile group foundation structure were the design variables，the minimum cost for the construction of the sluice chamber and pile group foundation was the objective function，and the anti-sliding stability of the chamber structure，bearing capacity of the foundation，stress in the basement，strengths of the chamber and pile foundation structures，settlement of the chamber structure，and horizontal displacement at the top of piles were the main constraint conditions. Using the optimization module in the software ANSYS，the optimal design schemes for the overall sluice structure and chamber structure were obtained，respectively. Compared with the optimal design scheme for the chamber structure，the optimal design scheme for the overall sluice structure shows that the total cost in the sluice construction decreases by 2. 7%，and the horizontal displacement at the top of piles reaches the critical limit，demonstrating a better optimization effect.

Key words：sluice；pile foundation；soft soil foundation；structural design；optimal design；finite element

收稿日期：（2014 10 15 编辑：熊水斌）

作者简介：崔朕铭（1990—），男，博士研究生，主要从事水工结构研究。E-mail：314413178@ qq. com

基金项目：江苏省水利科技项目（2013565112）

中图分类号：TV66

文献标志码：A

文章编号：1006 7647（2016）01 0086 04