基于量纲理论的煤层瓦斯压力计算模型的优化

王双燕，程五一，张昱涵

(中国地质大学(北京)工程技术学院，北京100083)

基于量纲理论的煤层瓦斯压力计算模型的优化

王双燕，程五一，张昱涵

(中国地质大学(北京)工程技术学院，北京100083)

煤层瓦斯压力预测对煤与瓦斯突出和煤层安全开采意义重大。在陈连省等基于量纲分析建立的煤层瓦斯压力计算模型的基础上，通过重新进行量纲分析以及MATLAB数值模拟分析，利用已有的实测数据，针对其所建立的煤层瓦斯压力计算模型进行了重新建模和优化，新模型为整体的一个数学模型，避免了原分段数学模型带来的误差，使得煤层瓦斯压力的预测计算更为准确，可为煤层瓦斯压力的预测提供参考。

量纲分析;MATLAB建模;煤层瓦斯压力;计算模型优化

煤层瓦斯压力的预测对煤与瓦斯突出和煤层安全开采具有重要的意义。目前许多专家和学者在煤层瓦斯压力的预测方面已经做了大量的研究工作，如陈连省在《基于量纲理论的煤层瓦斯压力计算模型的研究》一文中［1］(以下简称《研究》)中利用了量纲分析方法，并采用数据之间的拟合关系得到了关于煤层瓦斯压力的计算模型，但该模型属于分段形式的数学模型且计算误差过大。为此，本文在量纲分析法的基础上，采用MATLAB软件进行数值模拟分析，并利用已有的实测数据，对其所建立的煤层瓦斯压力计算模型进行了重新建模和优化，从而提高了该计算模型的预测的精度和准确性。

1 煤层瓦斯压力计算模型设计

1．1 量纲分析

影响煤层瓦斯压力的主要因素有:煤层中瓦斯含量W、基岩厚度hj、泥岩厚度hn、岩层含砂率Rs、煤层的埋藏深度H、煤层中瓦斯吸附常数a、b等。

陈连省在《研究》一文中的量纲分析结果产生的π值为［1］

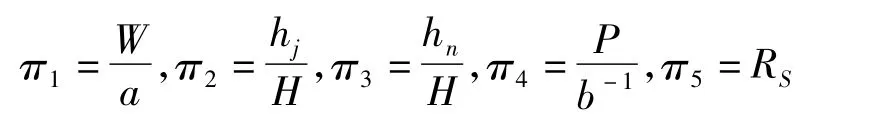
然而从计算得到的π3值可以发现，该值相对于其他π值来说非常小，在这种量纲分析的基础上进行MATLAB软件建模，计算机默认其值为0，说明从各个π值的相对关系来看，这种量纲分析方法弱化了π3的影响力度，即在一定程度上将泥岩厚度hn对煤层瓦斯压力的影响弱化了。

通过重新选取量纲分析中的基本物理量来计算π值，可以解决这一弊端。本文选择长度L、质量M、时间T作为基本量纲，可以得到各个影响因素的量纲表达式，详见表1。

煤层瓦斯压力的数学模型可表示为

根据Buckingham定理，所涉及的物理量总数n=8、基本量纲的个数m=3，根据π定理，可以得到π1、π2、π3、π4、π5无量值，选取a、b、hn为基本物理量，可得

即为

则煤层瓦斯压力的数学表达式可表示为

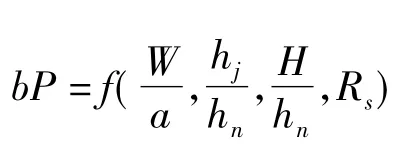
1．2MATLAB软件建模

在不清楚各变量之间关系的前提下，一般选取指数方程作为拟合方程［4］，即设煤层瓦斯压力的数学模型为

MATLAB软件数学分析应用数据见表2。陈连省在《研究》一文给出的煤层中瓦斯吸附常数a=21．37 m3/t，b=0．072 3 MPa－1。

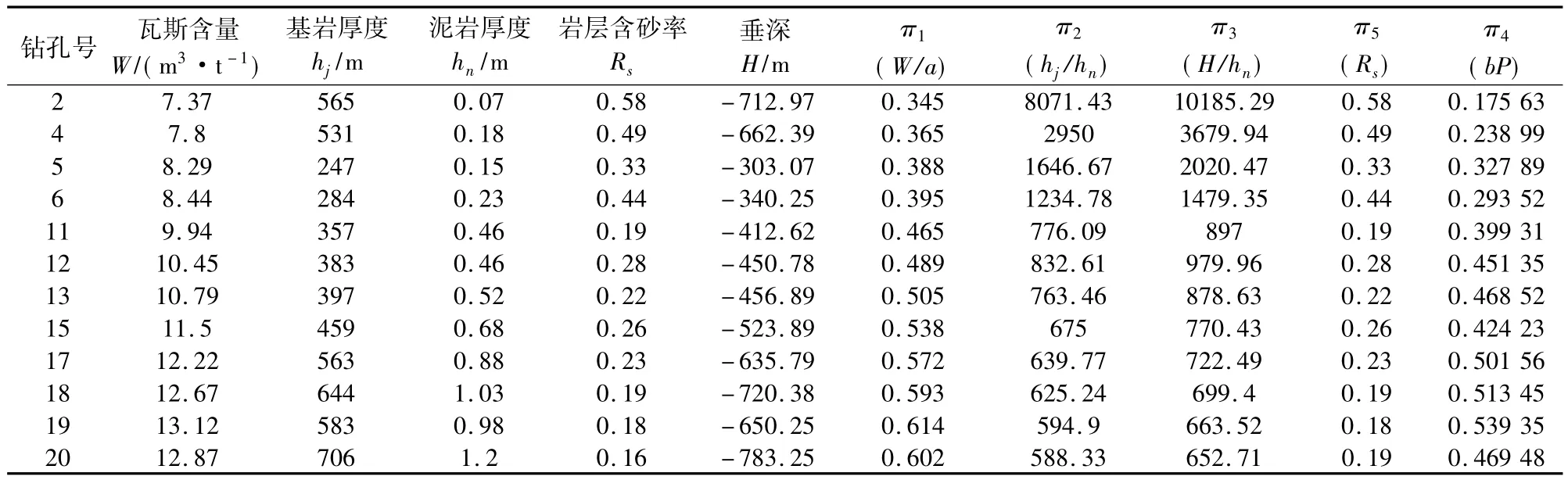
表2 MATLAB软件数学分析应用数据Table 2 Data of mathematical analysis by MATLAB software

表2的应用数据与《研究》中的相比，缺少了钻孔1的数据，主要基于两点原因:一是为避免各π值差异太大而修改了的量纲表达式中hn是作为分母存在的，而钻孔1数据中的hn值为0，不能顺利计算π2、π3的值;二是根据《研究》中所建立的模型计算得到的误差值可以发现，钻孔1的计算误差远远高于其他数据的计算误差，存在因数据不准确而影响模型准确性的可能。结合以上两点，决定去掉钻孔1的数据，因此本文建立的煤层瓦斯压力计算模型存在另外一个限制条件:所测煤层瓦斯压力的区域泥岩厚度不为0。

另外，从所选取的拟合方程可以发现，存在的变量有5个，如果直接以非线性的形式在MATLAB软件中进行数植模拟，复杂度及难度会很大，因此，令:

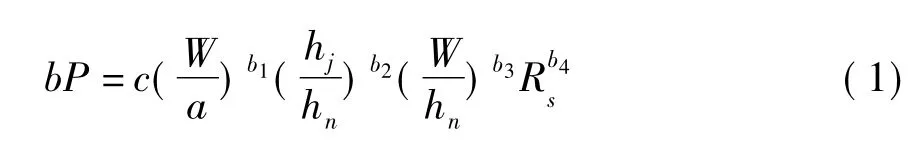
两边同时变换为对数形式，有

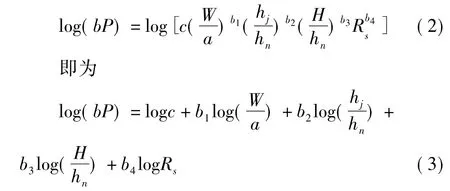
可见，将非线性式(1)变换为等价的线性式(3)可以大大地降低拟合的难度，而利用MATLAB软件进行拟合计算后，可得

式(4)即为煤层瓦斯压力的计算模型。

2 煤层瓦斯压力计算结果及误差分析

由于各类物理量数据的采集是具有范围的，因此式(4)也具有一定的适用范围。由于在数据的选取以及量纲分析的过程中，已经默认泥岩厚度hn的值不为0，即hn＞0，因此由建立的计算模型可知:当即煤层瓦斯压力P→0。

根据已有的煤层瓦斯压力实测数据，并利用本文建立的煤层瓦斯压力计算模型计算得到的煤层瓦斯压力值(即计算值1)与《研究》中的煤层瓦斯压力计算值(即计算值2)及其误差进行了对比，见表3。另外，采用Origin绘制了煤层瓦斯压力计算值及其误差对比图，见图1。由图1可以直观地发现，利用MATLAB软件进行拟合的结果更贴近于实测煤层瓦斯压力曲线。

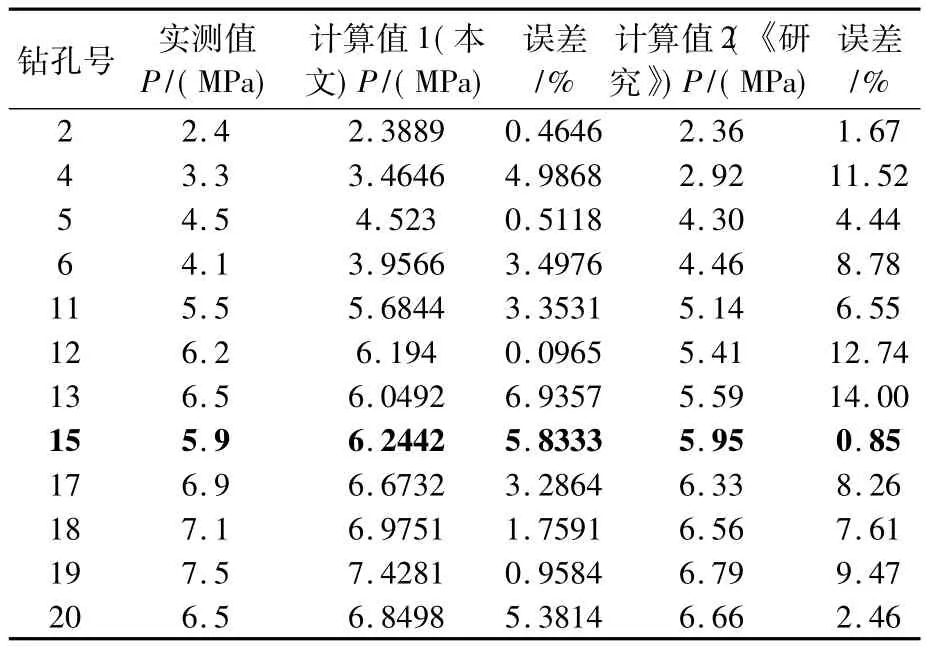
表3 煤层瓦斯压力计算值与实测值的误差对比Table 3 Calculation values of the coal seam gas pressure and comparison of the errors

此外，由表3和图1可见，仅15号钻孔本文模型的计算误差比《研究》模型的计算误差大，且在13号钻孔、17号钻孔两个模型(本文模型和《研究》模型)的计算值与实测值的误差都相对较大，但整体上本文模型的计算误差更低些，而在13号钻孔、15号钻孔、17号钻孔处出现了误差相对较大的波动不排除数据的采集过程等对计算结果的影响。

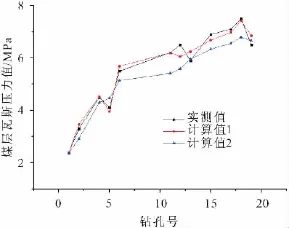
图1 煤层瓦斯压力计算值与实测值的误差对比图Fig．1 Comparision of the computation and monitoring values of the coal seam gas pressure

3 结论

本文在陈连省基于量纲分析建立的煤层瓦斯压力计算模型的基础上，利用量纲分析方法进行重新建模，结合MATLAB数值拟合分析得到新的煤层瓦斯压力计算模型，弥补了《研究》中所存在的缺陷，进一步提高了模型的计算精度及准确度，并得到如下结论:

(1)通过改进量纲分析中选取的基本物理量，得到了最优的几何参数，并对煤层瓦斯压力进行了重新建模。

(2)针对五维的非线性拟合方程进行数学等价变换，在不影响准确度的情况下降低了MATLAB编程的复杂度。

(3)依据已有的数据库进行MATLAB数值拟合，得到新的计算模型，计算结果表明新建模型降低了误差值，极大程度地提高了准确度。

［1］陈连省．基于量纲理论的煤层瓦斯压力计算模型的研究［J］．安全与环境工程，2013，20(2):136-141．

［2］付泽民．基于量纲分析法的金属板材折弯回弹数学模型［J］．机械工程学报，2010，46(12):53-58．

［3］王超．基于缩尺模型的桥式抓斗卸船机安全评估研究［D］．广州:广东海洋大学，2014．

［4］王振华．基于高温含尘烟气净化用纤维滤料织物特性研究与应用［D］．上海:东华大学，2013．

Optimization of the Calculation Model of Coal Seam Gas Pressure Based on the Dimensional Theory

WANG Shuangyan，CHENG Wuyi，ZHANG Yuhan
(College of Engineering and Technology，China University of Geosciences，Beijing100083，China)

It has great significance to predict the coal seam gas pressure for the coal and gas outburst and safety mining of coalbed．On the basis of the coal seam gas pressure calculation model by dimensional analysis by Chen Liansheng et al．，through the dimensional analysis and MATLAB numerical simulation analysis，this paper rebuilds and optimizes the model by using the existing measured data．The new model is a continuous mathematical model which avoids the error of piecewise mathematical model and makes the forecast of coal seam gas pressure more accurate．The model provides reference for the forecast of coal seam gas pressure．

dimensional analysis;MATLAB modeling;coal seam gas pressure;calculation model optimization

X936;TD712

ADOI:10．13578/j．cnki．issn．1671-1556．2016．05．026

1671-1556(2016)05-0155-03

程五一(1963—)，男，博士，教授，主要从事安全技术方面的研究。E-mail:cwy@cugb．edu．cn

2016-04-20

2016-08-07

王双燕(1993—)，女，硕士研究生，主要研究方向为工业安全管理。E-mail:wsy437755454@163．com