自由左交换代数的子代数*

李 羽

（惠州学院 数学系, 广东 惠州 516007）

自由左交换代数的子代数*

李 羽

（惠州学院 数学系, 广东 惠州 516007）

本文通过研究自由左交换代数的子代数的生成元的首项之间的关系证明了自由左交换代数的二元生成的子代数也是自由左交换代数.

左交换代数; 正规字; 子代数

1 引言

自由群的子群也是自由群[1]是群论中的一个著名的定理. 若一个代数范畴满足自由代数的子代数还是自由的, 则被称为Schreier范畴. Kurosh[2]证明了非结合代数范畴是Schreier范畴. Shirshov[3]和Witt[4]证明了李代数范畴是Schreier范畴. 在[5]中, Shirshov证明了交换(反交换)非结合代数范畴是Schreier范畴. Shestakov和Umirbaev[6]证明了Akivis代数范畴是Schreier范畴.

另一方面, 结合代数范畴不是Schreier范畴[7]. Bokut, Chen和Zhang[8]证明了Novikov代数范畴不是Schreier范畴. Kozybaev, Markar-Limanov和Umirbaev[9]证明了自由右对称代数的二元生成的子代数仍是自由右对称代数. Kozybaev[10]构造了自由右对称代数的一个五元生成的非自由子代数.

设k是一个域, A是k上的一个非结合代数. 若A满足恒等式x(yz)=y(xz), 则称A是一个左交换代数. Novikov代数范畴[11]和对偶莱布尼兹代数范畴[12]都是左交换代数范畴的子范畴. 自由左交换代数最早由A. Dzhumadil'daev 和C. Löfwall[11]所研究, 他们在[11]中给出了自由左交换代数的线性基底. 本文应用组合代数的方法重写自由左交换代数的子代数的生成元证明了自由左交换代数的二元生成的子代数也是自

由左交换代数.

2 自由左交换代数

设X是一个良序集. 设u, v分别是次数为m, n的非结合字, 那么我们称(uv)是次数为m+n的非结合字, 用d(uv)表示(uv)的次数. 令X**为X上的全体非结合字所构成的集合. 设u, v∈X**.

规定若d(u)＞d(v),

则u＞v.

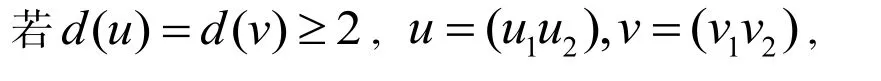
则规定u＞v

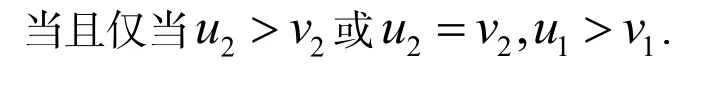
我们称这个序为次数逆字典序. 如无特别说明,文章将使用次数逆字典序.

定义1. 每一个字母xi∈X 被称为次数为1的正规字, 设u=(vw)是次数为m, m＞1的非结合字, 那么u=(vw)被称为次数为m的正规字, 如果v, w都是正规字且若w=(w1w2), 则v≥w1.

设k是一个域, N(X)为所有X上的正规字所构成的集合, kN(X)是由N(X)张成的域k上的向量空间.下面定义kN(X)上的乘法：

设u, v∈N(X), 若v=xi∈X ,

则令u· v=(uxi); 若v=(v1v2)且u≥v1,

则令u· v=(u(v1v2)); 若v=(v1v2)且u＜v1,

则令u· v=(v1(u· v2)).

定理1 ([11]). kN(X)关于乘法“·”构成了一个由X生成的自由左交换代数, 记为LC(X).

由定理1可知, 对于任意0≠f∈LC(X), f可以被唯一地表示成f=α1u1+α2u2++αnun,

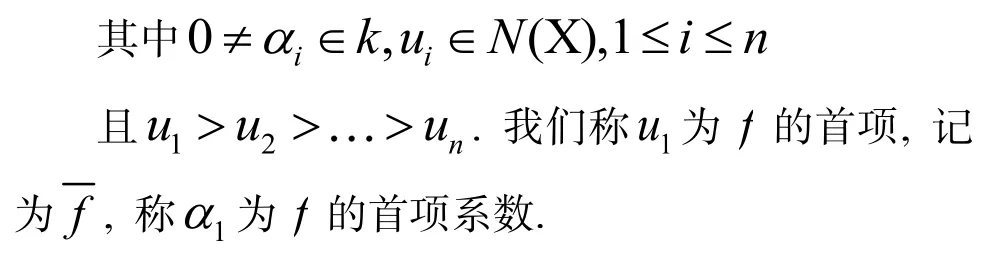
设f∈LC(X), 用Lf表示作用在LC(X)上的左乘算子, 即: Lf(u)=(fu), u∈LC(X). 特别地,

如果

那么

引理1. 每一个正规字u∈N(X)都可以被唯一地表示成

其中

证明：对d(u)作数学归纳法. 若d(u)=1,u=xi, 则原命题显然成立.

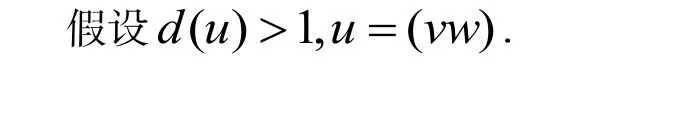
由归纳假设可知w=LwnLw1(xi),

其中n≥0, xi∈X , wj,1≤j≤n都是正规字且wn≥≥w1.

因为u是正规字, 所以v≥wn,

从而有

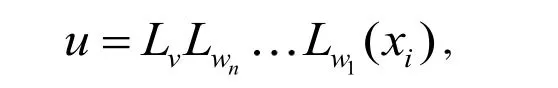
其中n≥0, xi∈X , v, wj,1≤j≤n都是正规字且v≥wn≥≥w1. 证毕.

引理2. 设u, v∈N(X)且v=LvnLv1(xi),

其中n≥1, xi∈X.证明：对n作数学归纳法.

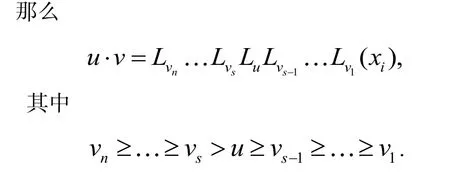
综上可得当n=1时原命题成立.考虑n＞1的情形. 若u≥vn,

则u· v=LuLvnLv1(xi)原命题显然成立.

若u＜vn,

则u· v=vn(u· Lvn-1Lv1(xi)).根据归纳假设得u· Lvn-1Lv1(xi)=Lvn-1LvsLuLvs-1Lv1(xi),

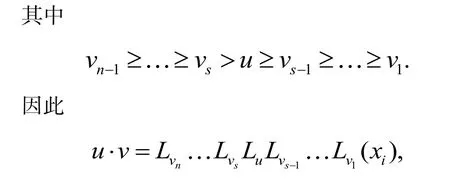
其中 vn≥≥vs＞u≥vs-1≥≥v1. 证毕.

引理3. ([11]) 若u, v, w∈N(X)且u＞v,

则 u· w＞v· w, w· u＞w· v .

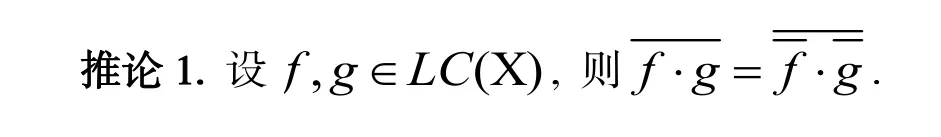
3 二元生成的子代数

引理4. 设f是LC(X)的任意一个非零元. 那么LC(X)的由f所生成的子代数也是自由左交换代数且f是这个子代数的自由生成元.

证明：假设f是代数相关的. 那么存在一个非零多项式p(y)∈L(y)使得在LC(X)中有p(f)=0成立. 设

定理2. 自由左交换代数的二元生成的子代数也是自由左交换代数.

根据引理[4]可知f1,f2是一个以g为自由生成元的自由左交换代数. 证毕.

[1] SCHREIER O. Die Untergruppen der freien Gruppen[J]. Abh. Math. Sem. Univ. Hamburg,1927(5)∶161 – 183.

[2] KUROSH A G. Nonassociative free algebras and free products of algebras[J]. Mathematical Sbornik,1947(62)∶239 – 262.

[3] SHIRSHOV A I. On subalgebras of free Lie Algebras[J]. Mathematical Sbornik,1953(33)∶ 441 – 453.

[4] WITT E. Die Unterringe der freien Lieschen ring[J]. Mat. Z.,1956(64)∶195 – 216.

[5] SHIRSHOV A I. On subalgebras of free commutative and anti-commutative algebras[J]. Mathematical Sbornik,1954(76)∶ 81-88.

[6] SHESTAKOV P I, UMIRBAEV U U. Free Akivis Algebras, Primitive Elements, and Hyperalgebras[J]. Journal of Algebra, 2002(250)∶ 533 –548.

[7] BOKUT L A, KUKIN G P. Algorithmic and combinatorial algebra[M]. Dordrecht∶ Kluwer Academic Publishers,1994.

[8] BOKUT L A, CHEN Y Q, ZHANG Z R. Gröbner–Shirshov bases method for Gelfand–Dorfman–Novikov algebras[J]. Journal of Algebra its Applications, DOI∶ 10.1142/S0219498817500013

[9] KOZYBAEV D, MAKAR-LIMANOV L, UMIRBAEV U. The freiheitssatz and automorphisms of free right-symmetric algebras[J]. Asian-European Journal of Mathematics,2008(1)∶ 243 – 254.

[10] KOZYBAEV D. On the structure of universal multiplicative algebras of free right-symmetric algebras. Vestnik KazNU,2007(3)∶3 – 9.

[11] DZHUMADIL′DAEV A, LöFWALL C. Trees, free right-symmetric algebras, free Novikov algebras and identities[J]. Homology, Homotopy and Applications,2002(4)∶ 165 – 190.

[12] LODAY J-L. Cup product for Leibniz cohomology and dual Leibniz algebras[J]. Mathematica Scandinavica,1995(77)∶189 – 196.

【责任编辑：吴跃新】

Subalgebras of Free Left-commutative Algebras

LI Yu
(Department of Mathematical Sciences, Huizhou University, Huizhou 516007, Guangdong China)

In this paper, we prove that two generated subalgebras of free left-commutative algebras are also free by the research on the relations between the leading terms of the generators of subalgebras of free left-commutative algebras.

Left-commutative algebra; Normal word; Subalgebra

A

1671 - 5934 (2016)03 - 0084 - 05

2016 -

国家自然科学基金项目(Nos. 11401246; 11426112; 11501237), 广东省自然科学基金项目（Nos.1414050000365; 1414050000488）, 广东高校优秀青年教师培养计划项目（No.YQ2015155）, 惠州学院博士科研基金项目（Nos. C513.0210; C513.0209）.

李 羽（1982 - ）, 广东龙门人，讲师，博士，研究方向为组合代数及其应用.