坐标测量机孔径测量的不确定度评定模型研究

徐　磊，陈晓怀，程银宝，姜　瑞，王汉斌，程真英

（合肥工业大学仪器科学与光电工程学院，安徽合肥230009）



坐标测量机孔径测量的不确定度评定模型研究

徐磊，陈晓怀，程银宝，姜瑞，王汉斌，程真英

（合肥工业大学仪器科学与光电工程学院，安徽合肥230009）

摘要：以坐标测量机测量孔径为例，阐述测量过程中影响测量结果的不确定度来源，根据测量模型建立孔径测量的GUM法不确定度评定模型；利用对坐标测量机的测量系统量值特性指标分析的方法，给出基于量值特性分析法的各标准不确定度分量的评定模型。通过对汽车空调压缩机后缸体的孔径测量，比较两种方法评定的扩展不确定度。实例分析可以看出：对于坐标测量机复杂的非线性测量模型，GUM法在计算灵敏系数时，运算量较大且获得的是近似结果，因此其可操作性不强；量值特性分析法通过对测量系统整体的分析，基于大量的实验数据对测量结果进行测量不确定度评定，其流程和操作性更为便捷、有效。

关键词：计量学；不确定度评定；孔径测量；坐标测量机

0　引言

测量不确定度是表征赋予被测量值分散性的非负参数。一个完整的，有意义的测量结果应包含被测量值的估计与分散性参数两个部分[1]。测量结果的可用性很大程度上取决于其测量不确定度的大小。随着科技的快速发展，为了满足更高的工业要求，测量数据的准确性与可靠性也就愈加重要，而提高精密测量的准确度，则需多角度分析影响测量结果的因素，采用正确的评定方法对测量不确定度进行评价[2]，从而量化各因素对测量结果的影响，为提高精密测量的准确度提供方向。

三坐标测量机（coordinate measuring machine，CMM）是一种高效、万能的精密测量仪器，主要用于工件尺寸、形状和位置等几何量参数的测量，在现代制造工业领域和科学研究中的应用极为广泛。由于CMM是极其复杂的几何量测量仪器，与单一测量对象的比较型测量仪相比，针对CMM进行面向任务的测量不确定度评定异常困难。不仅因为CMM测量策略的多样性使得其不同测量任务的不确定度评定过程和结果大相径庭，且影响CMM测量不确定度的误差源因素很多，诸误差源与测量结果的传递关系难以确定。因此现有的三坐标测量机的测量结果通常只有被测参数的估计值，不能给出相应的测量不确定度[3]。本文以孔径测量为例，在测量系统量值特性分析的基础上，对CMM面向任务的测量不确定度评定模型进行研究。

1　测量模型

CMM通过间接测量得到圆的直径，即由采样点在最小二乘法的约束下，得到最佳拟合圆。

在X-Y平面内的直角坐标系下，圆的方程为

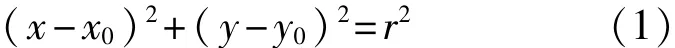
令a=2x0，b=2y0，c=r2-x02-y02，l=x2+y2，则式（1）展开并线性化有：

l=ax+by+c

对应拟合圆时所采的测量点Pi，则有正规方程组：

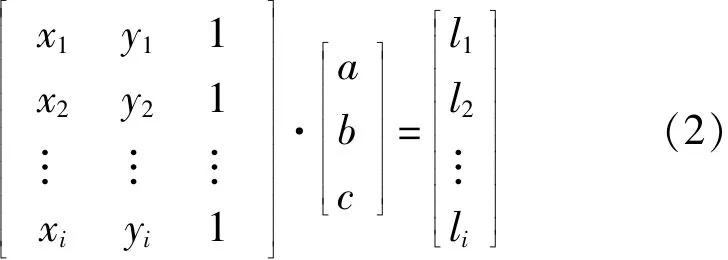
求解方程组（2）即可得到a、b、c，从而得出直径测量的数学模型：

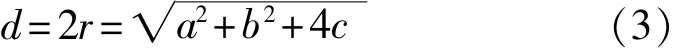
在圆的实际测量和评定过程中，一般会对采样点附加约束条件，即测量采样点数量为偶数，且在被测圆周上等间距分布[4]。在此约束条件下最小二乘圆的圆心坐标为

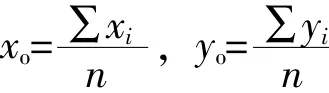
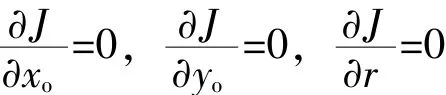
则式（3）可简化为

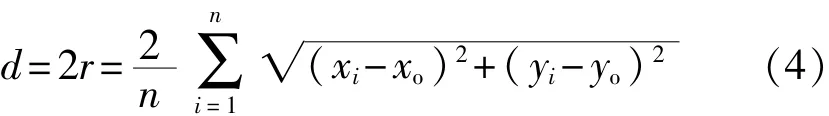
2　GUM解析法评定测量不确定度模型

CMM测量孔径时，影响测量结果的主要误差源包括仪器自身的21项机构误差、测量重复性误差、热变形误差、力变形误差、探测系统误差、动态测量误差等等。因此，CMM孔径D测量的一般数学表达式为

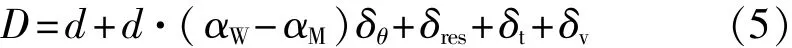
式中：d——测量模型的输出直径值；

αW——工件的热膨胀系数；

αM——CMM光栅尺的热膨胀系数；

δθ——实际测量温度与标准温度（20℃）的差值；

δres——示值误差对测量结果的影响；

δv——测量力对测量结果的影响；

δt——动态误差对测量结果的影响。

待测孔径D是关于输入量d、δθ、δres、δv、δt的函数，即：

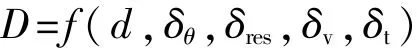
输入量之间互不相关，根据测量不确定度表示指南（GUM）可得各传递系数为

于是，CMM测量孔径D的合成标准不确定度为

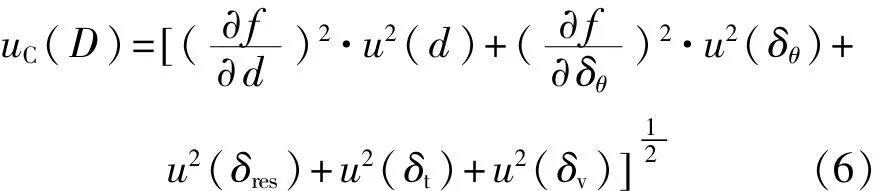
同理，u（d）也可分析得到。由式（4）知：

d=g（xi，yi，x0，y0）

则各传递系数为

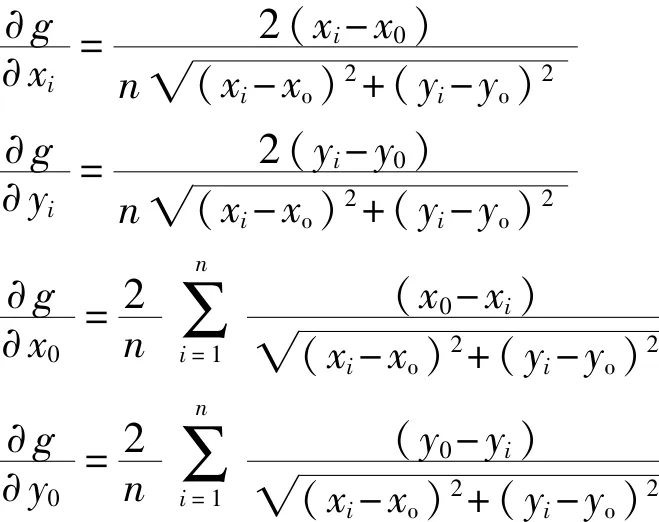
于是

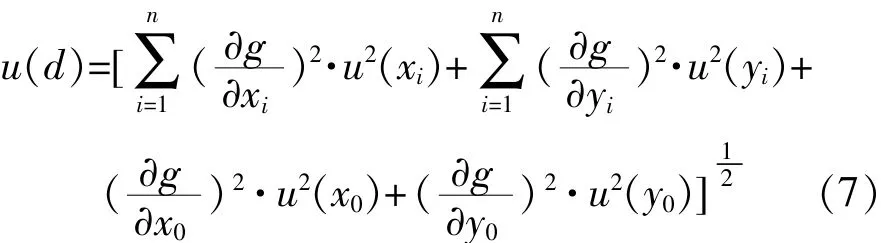
将式（7）求得u（d）代入式（6）即得到被测孔径D的测量不确定度。

3　量值特性分析法评定不确定度

测量系统是指用来对被测量进行赋值时的操作程序、人员、标准件、设备、环境及软件等要素的综合，涵盖获取测量结果的整个过程。完整的测量过程难免存在很多的误差源，包括被测量定义的不准确、被测量的采样样本不全面、环境条件不稳定以及对环境影响的认识不充分、人员操作、测量仪器的分辨率或鉴别阈的限制、测量标准标定值的不准确、测量策略、测量程序和数据处理不准确、系统误差修正不完善以及各随机误差的影响等。虽然测量系统组成要素不同，上述误差源对不确定度的贡献度有所差异，但对整个测量系统的综合因素存在共性。因此，美国三大汽车公司（Ford、GM、Chrysler）联合编写的QS9000配套手册《测量系统分析》提出了用测量系统分析法对测量系统进行不确定度评价。本文基于测量系统分析提出用6个量值特性来全面评价CMM面向任务的测量不确定度，即分辨力、偏移、线性、稳定性、重复性和复现性。使用统计分析或图表法分析测量系统的误差，上述量值特性指标基本反映了测量过程的不确定性，即涵盖了引起测量系统不确定度的主要来源[5-8]。

3.1标准不确定度分量

1）偏移和线性所引起的不确定度分量uE

三坐标测量机的线性和偏移在尺寸测量中以示值误差E来表征，安全起见一般以最大允许示值误差MPEE考虑，取均匀分布，则该标准不确定度分量的数学模型为

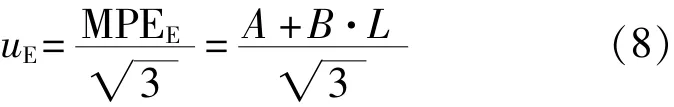
式中，MPEE=A+B·L一般由仪器说明书给出[9]。

2）重复性所引起的不确定度分量uRT

重复性测量指在相同的条件下对同一被测量进行多次测量的一组操作，即相同的测量策略、人员、仪器、环境、被测件。重复性是测量仪器重要的误差来源，反映的是随机误差对测量结果的影响[10]，以n次重复测量的测量值的实验标准偏差s（xk）来表征。

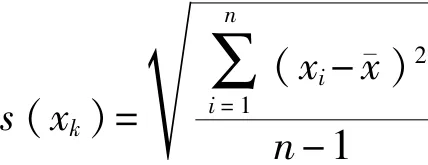
若最终的测量结果采用N次测量值的平均值表示，则有：

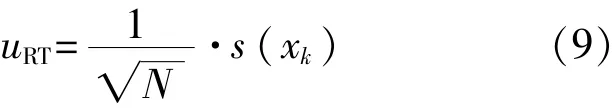
显然，若最终的测量结果采用单次测量值表示，则uRT=s（xk）。

3）复现性所引起的不确定度分量uRD

复现性指在测量条件、人员、仪器、测量方法和原理等发生变化的情况下，对同一或类似被测对象进行多组测量的精密度[11]，可以用多组测量平均值之间的实验标准偏差定量表示。

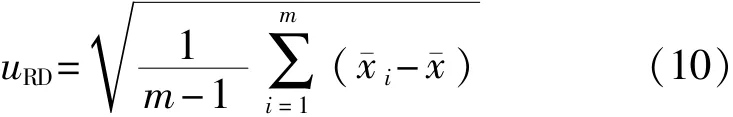
其中：

4）稳定性所引起的不确定度分量uS

测量稳定性是同一测量人员在同一环境下，使用同一测量仪器对同一工件的相同被测参数在不同时间下测量值的偏移，偏移越小则稳定性越好。对于不同的CMM稳定性所引起的不确定度分量的大小也不尽相同。如对于纳米三坐标机，稳定性所引起的不确定度分量是一个不可忽略的重要来源。而对于普通CMM，稳定性所引起的不确定度分量通常可忽略不计。同理，也是通过多组测量计算测量列平均值的标准偏差来表征，标准不确定度分量的数学模型与复现性相同，只是各组测量列是在测量条件不变的情况下获得。

5）分辨率所引起的不确定度分量uR

读数时末尾的舍入将引起不确定度，且属于均匀分布。对于CMM而言，分辨率较高且为数显，所以分辨率所引起的不确定度分量常忽略不计。若分辨率为a则不确定度分量按B类评定为

6）温度补偿引入的不确定度分量utemp

CMM作为一种精密的仪器，温度变化对其影响不可忽略。温度改变时，由于热胀冷缩原理，被测工件尺寸以及光栅尺尺寸都将发生改变。虽然CMM通过温度补偿技术减小温度误差的影响，但补偿后的误差仍不可忽略。误差模型如下：

ΔL=L（T-20）（αW-αM）

式中：L——被测工件尺寸；

T——测量时的实际温度；

αW——工件的热膨胀系数；

αM——光栅尺的热膨胀系数。

根据误差模型可知温度补偿引入的不确定度分量含有以下3个部分：

①被测工件热膨胀系数所引起的不确定度分量uT1，设工件热膨胀系数在±ΔαW范围内按正态分布（k=2）变化，则：

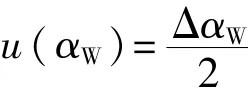
于是工件热膨胀系数所引起的不确定度分量为

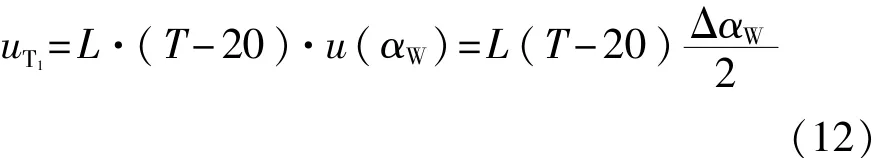
②同理，光栅尺热膨胀系数所引起的不确定度分量uT2为

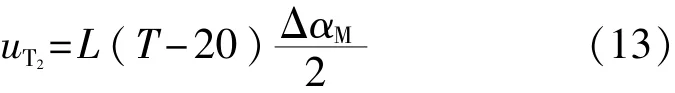
③假设实际测量时的温度T在±ΔT范围内按均匀分布变化，则：

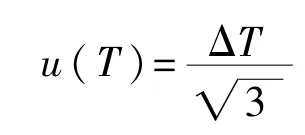
于是，温度变化所引起的不确定度分量uT3为

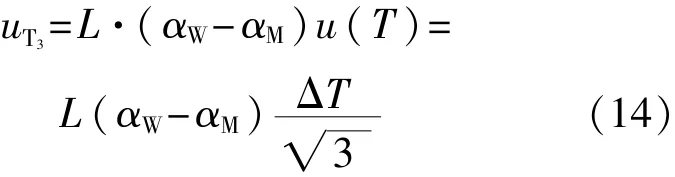
所以，温度补偿引入的标准不确定度分量为

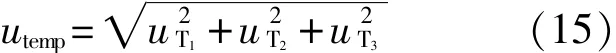
3.2不确定度合成

综上分析可知，各标准不确定分量相互独立，则量值特性分析法的合成标准不确定度为

4　实例分析

如图1所示，采用海克斯康MH3D-DCC型CMM测量某汽车空调压缩机后缸体的孔径，被测孔径标称尺寸为32mm。实验坐标测量机空间长度测量准确度MPEE≤（3+4L/1000）μm，光栅分辨率0.1 μm。被测工件和机器光栅尺的热膨胀系数以及变化范围分别为

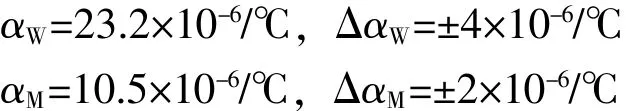
将工件摆放在工作平面的中央，记录测量环境，采取自动测量的方法，锁定Z轴。在同一圆截面上等间距采样8个点来评价被测圆的直径。

4.1GUM法实验结果

重复测量10次获得各采样点的坐标值，计算单点坐标的u（xi）、u（yi），安全起见，选取其中的最大值作为最终的评价数据。通过实验数据得u（xi）≈u（yi）≤2μm，则u（x0）≈u（y0）≤0.71μm。各采样点的坐标值传递系数如表1所示。

图1　孔径测量实验

表1　采样点的坐标值传递系数

则根据式（7）计算得u（d）=1.43 μm。实验采用自动测量，测速较慢，测量力所引起的误差和动态误差可忽略不计。根据被测工件的标称尺寸计算知u（δres）=1.81 μm。实验室温度控制在（20±1）℃，则δθ=1℃，考虑均匀分布，计算得：

根据式（6）计算合成标准不确定度为uC（D）= 2.3μm。按置信概率P=95%取包含因子k=2，则GUM法获得测量结果的扩展不确定度为U=k·uC（D）=4.6μm。

4.2量值特性分析法实验结果

CMM 6个量值特性指标中，对于示值误差、分辨率与温度补偿所引起的不确定度分量，可直接根据CMM使用手册与实验环境结合上述不确定度评定模型直接计算。而重复性、复现性、稳定性所引起的不确定度分量则需要通过实验数据来分析计算。

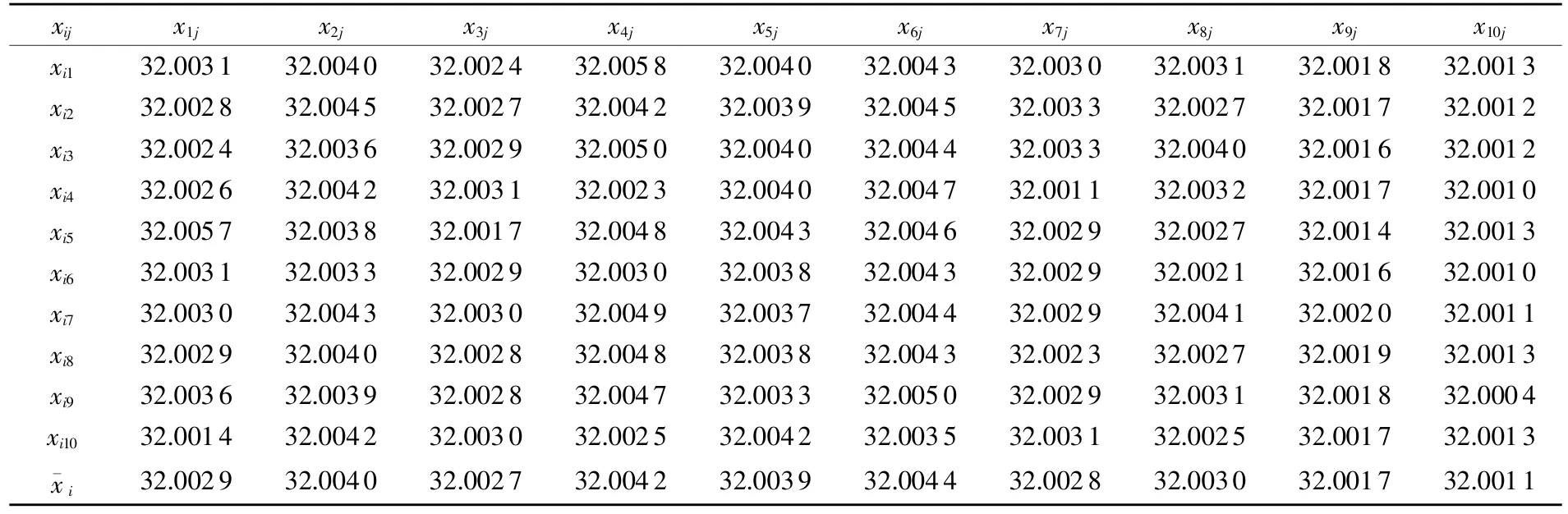
表2　测量复现性检测数据mm

复现性检测数据如表2所示，由不同测量人员在改变测头型号、工件位置（包含工作平面4个对角线的顶点位置）、采样点数等条件下得到。在复现性试验中取等间距采8点的实验数据作为重复性检测数据。

稳定性检测由同一测量人员在相同的测量环境下，每隔1h对被测参数进行一次重复测量。稳定性检测数据如表3所示。根据上述检测数据与检测环境，由式（8）～式（15）计算出各标准不确定度分量，如表4所示。

表3　测量稳定性检测数据

表4　标准不确定度分量

明显可见稳定性与分辨率所引起的不确定度分量属于微小量，可忽略不计，且测量重复性与仪器分辨率存在线性关系，分辨力越高重复性往往越明显，不确定度评定中只考虑两者中较大的一项即可。由式（16）得合成标准不确定度uC=2.2 μm。同样，按置信概率P=95%取包含因子k=2，则量值特性分析法获得测量结果的扩展不确定度为U=k·uC=4.4μm。

表5　GUM法与量值特性分析法的评定结果

5　结束语

基于GUM法与量值特性分析法评定出的CMM孔径测量的扩展不确定度如表5所示。

可以看出两种方法的不确定度评定结果比较接近，从两种方法的评定过程可以看出，量值特性分析法略过求解测量模型以及传递系数的过程，有效简化了测量不确定度的评定流程。当CMM测量模型为非线性等复杂的数学模型时，量值特性分析法大大降低测量人员评定测量不确定度需要的专业知识和评定经验方面的限制，给不确定度评定提供了一种准确快捷的方法，具有良好的应用前景和实用价值。

参考文献

[1]测量不确定度评定与表示：JJF 1059.1—2012[S].北京：中国质检出版社，2012.

[2]王鹏，王明泉，韩婧.导爆索内径尺寸测量不确定度的评定及数据处理模型[J].中国测试，2014，40（2）：31-35.

[3]李红莉，陈晓怀，王宏涛.坐标测量机测量端面距离的不确定度评定[J].中国机械工程，2012，23（20）：2401-2404.

[4]连慧芳.形位误差测量的不确定度评定[D].合肥：合肥工业大学，2010.

[5]谢少锋，陈晓怀，张勇斌.测量系统不确定度分析及其动态性研究[J].计量学报，2002，23（7）：237-240.

[6] FENG C X，SAAL A L，SALSBURY J G，et al. Design and analysis of experiments in CMM measurement uncert ainty study[J]. Precision Engineering，2007，31（2）：94-101.

[7]王秉刚，TUNG K.测量系统分析[M]. 3版.天津：中国汽车技术研究中心，2002：190-201.

[8]谢少锋.测量系统及其分析方法综述与分析[J].电子质量，2001（12）：18-19.

[9] Geometrical Product Specifications（GPS）-Acceptance and reverification tests for coordinate measuring machines-Part 1:Vocabulary：ISO 10360-1：2000[S].2000.

[10]齐皇仲，叶怀储，陈欢，等.微小深度尺寸测量系统的误差与测量不确定度分析[J].中国测试，2013，39（z2）：116-117.

[11]叶德培.测量不确定度理解评定与应用[M].北京：中国质检出版社，2013：26-27.

（编辑：刘杨）

Uncertainty evaluation model for aperture measurement of coordinate measuring machines

XU Lei，CHEN Xiaohuai，CHENG Yinbao，JIANG Rui，WANG Hanbin，CHENG Zhenying
（School of Instrument Science and Opto-electronics Engineering，Hefei University of Technology，Hefei 230009，China）

Abstract:The factors which may influence the measurement uncertainty of aperture measurement by coordinate measuring machine（CMM）were analyzed. Two uncertainty models were established based on guide to the expression of uncertainty in measurement（GUM）and measurement system analysis（MSA）. Measurement uncertainty for aperture of workpiece were evaluated by the two methods. Moreover，seen from the evaluation example，the results of uncertainty evaluation obtained from GUM and MSA were compared，the comparison result indicates that GUM method needs large amounts of computation and can only get the approximate results in the calculation of sensitivity coefficient but MSA method analyses the whole measurement system and evaluates uncertainty through a large number of experimental data，which is more convenient and more effective than GUM method.

Keywords:metrology；uncertainty evaluation；aperture measurement；CMM

作者简介：徐磊（1993-），男，安徽滁州市人，硕士研究生，专业方向为测试计量技术及仪器。

基金项目：国家自然科学基金项目（51275148）合肥工业大学青年教师创新项目（JZ2014HGQC0126）

收稿日期：2015-05-29；收到修改稿日期：2015-07-08

doi：10.11857/j.issn.1674-5124.2016.01.006

文献标志码：A

文章编号：1674-5124（2016）01-0026-05