基于广义谐波小波的工频功率因数测量算法

张　媛，王　楠

（1.上海交通大学电子信息与电气工程学院，上海200240；2.中船重工705研究所上海工程技术部，上海200245；3.陕西理工学院机械工程学院，陕西汉中723001）



基于广义谐波小波的工频功率因数测量算法

张媛1，2，王楠3

（1.上海交通大学电子信息与电气工程学院，上海200240；2.中船重工705研究所上海工程技术部，上海200245；3.陕西理工学院机械工程学院，陕西汉中723001）

摘要：针对传统功率因数测量方法存在的问题，基于广义谐波小波的优良特性，结合功率因数定义，提出测量工频功率因数的广义谐波小波算法。该算法通过对采样离散化后的电压与电流信号进行工频提取，然后对其进行重构，最终结合功率因数定义来实现。建立算法的数学模型，对其进行仿真分析，最后通过液压系统实验对算法进行验证，提取出完全基于工频的功率因数。分析结果表明：与其他算法特别是与正交小波相比，基于广义谐波小波的工频功率因数测量算法速度快、精度高，测量误差＜3.5%，具有较好的工程实用价值。

关键词：广义谐波小波；功率因数；快速傅里叶变换；Mallat算法

0　引言

电工学中的功率因数（power factor，PF）是为了表征交流电源的利用率而引入的，其定义为有功功率P和视在功率S的比值，即PF=P/S=cosφ，式中φ为标准正弦波电压与电流的相位差[1]。然而，由于电力系统中非线性负荷的存在，以及电力电子负载的大批量使用，在实际工程应用中测得的电压、电流信号多为携带多种谐波分量的非正弦波[2]，谐波对电源利用率的影响已不能忽视；因此，为了消除谐波影响，提出准确、高效的工频功率因数测量方法就显得尤为重要。

传统的测量功率因数的方法主要有电压、电流过零点采样法，单片机/DSP测量法，功率因数表测量法，电压、电流互相关法，快速傅里叶变换（FFT），正交小波变换[3-8]等。过零点采样法的主要不足是温漂严重、抗干扰性差；传统FFT算法存在频谱泄露与栅栏效应。采用正交小波（db3）测量工频功率因数，则存在以下问题：1）Daubechies类小波没有明确的解析表达式，且相位非线性，故若要提取工频信号，会有相位损失，误差较大；2）经典正交小波变换基于Mallat算法，是“隔二抽取”的，因此，应用其提取的信号掺杂了其他频率成分，而且信号重构回时域的突变点多，容易失真；3）Mallat算法在分解过程中，后一层的分解依赖于前一层的结果，重构亦如此；而这一迭代过程，必将导致计算误差的传递和积累[6]。由功率因数的定义可知，准确获取基于工频的电压、电流相位差是测量功率因数的关键，即对带有多种谐波的电压、电流进行滤波；然而传统方法并不能有效消除谐波，特别是高次谐波的影响，而且在方法的应用方面还存在一些问题，因此准确度不高，存在一定局限性。

广义谐波小波是剑桥大学D.E.Newland教授于1994年提出的，是一种复小波，有明确的函数表达式，具有盒形频谱，频域紧支，不受二进制限制且分析频带灵活。其重要特征为：1）零相移特性；2）在不同分解尺度下，信号各分析频段采样频率和采样点数不变；3）分解算法是通过FFT和IFFT变换实现的，速度快，准确度高。因此自提出后，广泛用于微弱信号特征提取、故障诊断、信号滤波、电力系统谐波检测等方面[9-12]。

本文将广义谐波小波引入到对工频功率因数的测量中，建立了功率因数测量算法的数学模型，并对其进行仿真分析；最后结合液压系统实验对算法进行验证，准确提取出了完全基于工频的功率因数。

1　功率因数测量算法数学模型的建立

1.1广义谐波小波

广义谐波小波可描述如下：

设有正实数m，n（m＜n），考察频带[2mπ，2nπ]，给定步长k/（n-m），（k∈Z），k为频带分析中心，则广义谐波小波定义如式（1）所示，式中尺度参数n，m的取值是关键，其分别是分析频带的上下限，可参考式（2）选取。若信号的采样频率为fs，则第j层（j为非负整数）小波分析频宽为B=fs/2j+1。

可以看出，广义谐波小波对信号的分析不受二进制限制，频带选择灵活；随着分解层数j的逐渐增大，可以对信号整个分析频带进行无限细化。假定要处理的信号为x（t），经采样离散化后的序列为x（r），r=0，1，…，N-1，N为采样点数；其广义谐波小波变换公式为

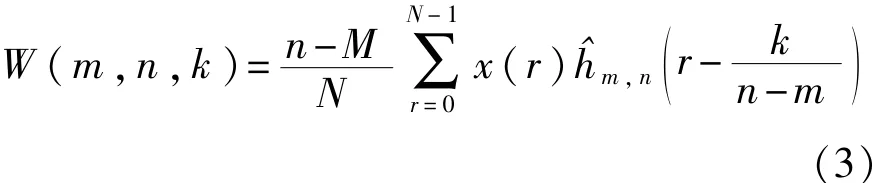
1.2功率因数测量算法数学模型

算法的数学模型建立如下：假定测得的非正弦电压、电流信号分别为un（t）、in（t），其中包含的工频电压、电流信号分别为u（t）、i（t）。上述信号采样离散化后的序列值分别为un（r）、in（r），u（r）、i（r），r= 0，…，N-1，N为总采样点数。首先应用广义谐波小波对信号un（r）、in（r）进行工频提取，结果如式（4）所示；然后重构信号u（r）、i（r），如式（5）所示。其中，m，n，k及分解层数j的选择可参考式（2）。功率因数可参照定义λ=cosφ=P/S求得，其中，有功功率P和视在功率S的求法如式（6）所示，N＇为每周期采样点数。经过以上处理过程，就可得到完全基于工频的功率因数。

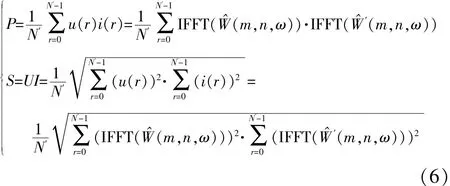
广义谐波小波是从频域定义的，是一个理想的带通滤波器；但作变换时，对其进行了时域截断，因此，它的频谱不是标准的“盒形”，产生了Gibbs现象（谐波小波本身并不会带来频泄）。对此，解决的办法是对其作加窗处理（如汉宁窗等），可以较好地消除Gibbs现象，提高测量精度。另外，由于广义谐波小波变换“一次到位”，即变换一次即可得到所有层的分解系数，因此没有积累误差，算法简洁、快速。

2　仿真分析

给出非正弦的电压、电流仿真信号，如下式所示：

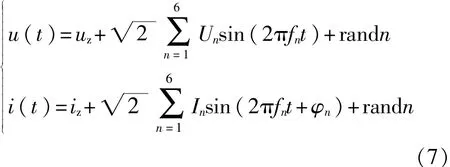
参数设置如下：采样频率fs=2 560 Hz；采样点数N=4 096；uz=50 V（电压直流分量）；iz=5 A（电流直流分量）；randn是均值为0，方差为1的高斯随机序列；U1～U6为220，110，50，200，150，100V；I1～I6为5，10，8，2，6，20 A；f1～f6为：50，25，120，100，150，250 Hz；φ1～φ6为π/4，π/6，π/8，π/3，π/4，π/4；分析频率fN=fs/2= 1 280 Hz；分解层数j=6，分析频宽B=fs/2j+1=20 Hz，下限频率m=40 Hz，上限频率n=60 Hz，频带中心k=10。

仿真时，在1s时突然改变50 Hz电流信号的相位为π/6，应用1.2中的算法数学模型对式（7）中的仿真信号进行变换，仿真结果如图1所示。由图可知，经广义谐波小波变换后，功率因数λ和相位差φ在1s时有一个跳变，分为两段；由于计算误差的存在，每段在刚开始约0.2 s内有较大波动，但过后将比较平稳，各个参数的比较见表1、表2。为验证本算法的效果，与目前较流行的正交小波提取功率因数方法的仿真结果进行比较，可以看出，与正交小波相比，应用广义谐波小波变换算法提取功率因数误差小、准确度更高；视在功率误差＜0.40%，相位差与功率因数则＜0.20%。

3　实验验证

3.1实验内容及参数设置

为了验证谐波小波功率因数测量算法及数学模型的实用性与准确度，在液压动力系统实验台上进行实验。实验台由变频电机、齿轮/柱塞泵、截止阀、溢流阀、换向阀、油马达以及各种传感器组成，可对液压系统各种工况下的运行状态进行监测、分析与故障诊断，可对信息进行多源融合。液压动力系统实验台原理如图2所示。实验内容如下：取齿轮泵单独工作工况，获取在系统载荷变化过程中（通过电磁溢流阀缓慢调压，调压范围为0～15 MPa）电机的电流信号、电压信号，采样频率为Fs=1 280 Hz，总采样点数为N=65536。当系统压力加至6，12 MPa时，同时用钳形功率表（型号：PROVA6601）分别测量电机有功、无功、视在功率及功率因数。

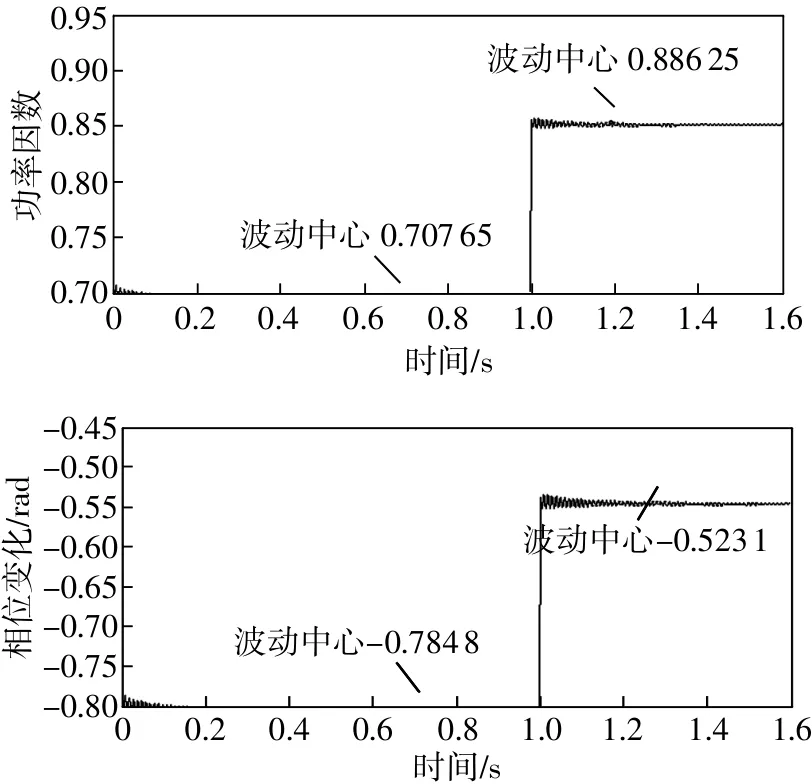
图1　广义谐波小波变换后的仿真结果

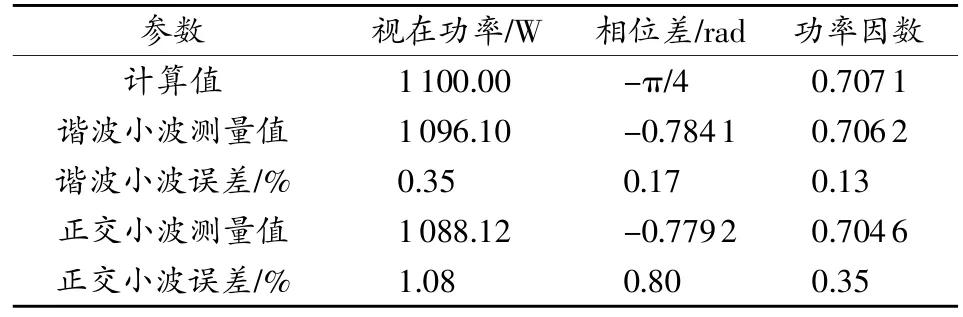
表1　0～1s内测量参数及误差

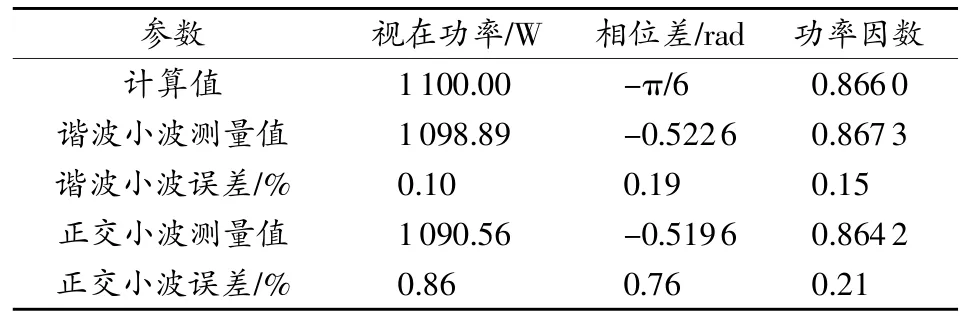
表2　1～1.6s内测量参数及误差

3.2实验结果及分析

钳形功率表测量结果如表3所示。图3是实测的电压、电流信号。由图可知，电压信号在系统载荷变化过程中基本保持不变，而电流信号则有明显变化，图中升压过程有明显两个凸台形状，分别与系统压力6，12 MPa对应。最高的凸台则与15 MPa对应。图4为用广义谐波小波变换后的工频电流信号及其功率谱图，分解层数为j=6，故分析频带B= 1280/27=10Hz，m=45，n=55，k=10，频带中心为50 Hz。由于存在频谱泄露，所以电流信号功率谱图上50 Hz附近出现了45，55 Hz两个谱峰。

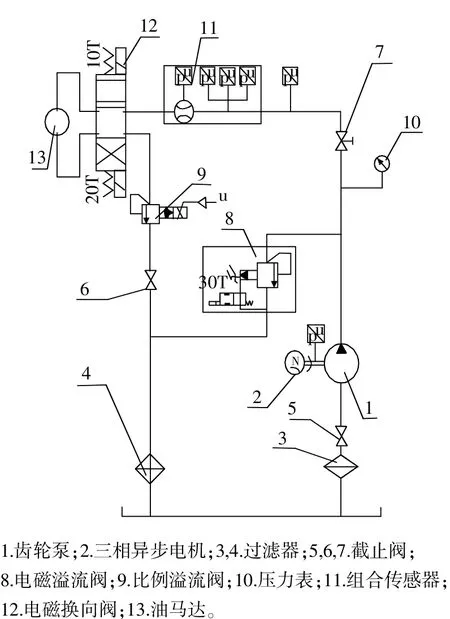
图2　液压动力系统实验台原理图

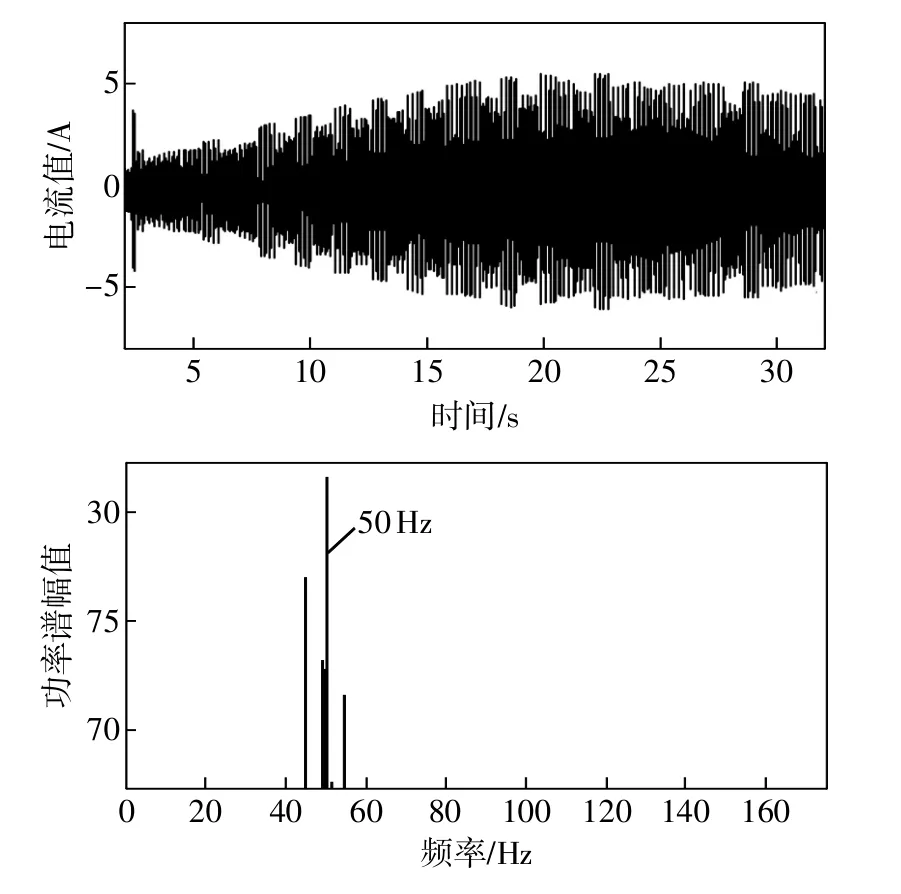
图4　谐波小波变换后的工频电流信号时频图

需说明的是，由于实验中的三相异步电机为三相三线制，故测得的电压信号是线电压，其幅值是相电压的倍、相位超前30°。故计算功率因数时，相位差亦相差30°。图4中的电压是经过幅值换算后的相电压，电流是相电流。功率因数λ可采用下式求出，θ是相电压和相电流的相位差：

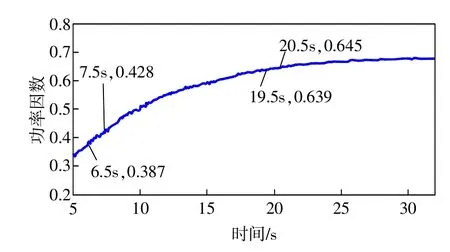
图5　谐波小波变换后的功率因数曲线

图5是经过广义谐波小波变换后的功率因数曲线，图6是图5中对应的两部分局部放大后的示意图。可以看出，功率因数曲线的变化趋势和电流基本相同。为了检测广义谐波小波测功率因数的算法准确度，在曲线上取测量时间段6.5～7.5s，19.5～20.5s（对应钳形功率表7，20s），通过求平均值获得功率因数（取50个正弦电流周期）。相应的也用正交小波对实测数据进行处理，计算结果与表3所测数据的对比如表4所示，表5为两种方法测量功率因数的误差对比。

可以看出，与功率因数表实测结果对比之后，应用广义谐波小波提取基于工频的功率因数误差＜3.5%，准确度大大高于正交小波处理结果。结合表1、表2的仿真结果分析表明，基于广义谐波小波的工频功率因数方法具有可行性以及较高的准确度。另外，由于实测数据为实时动态数据且复杂多变，因此，功率因数实测结果的误差远大于仿真结果。

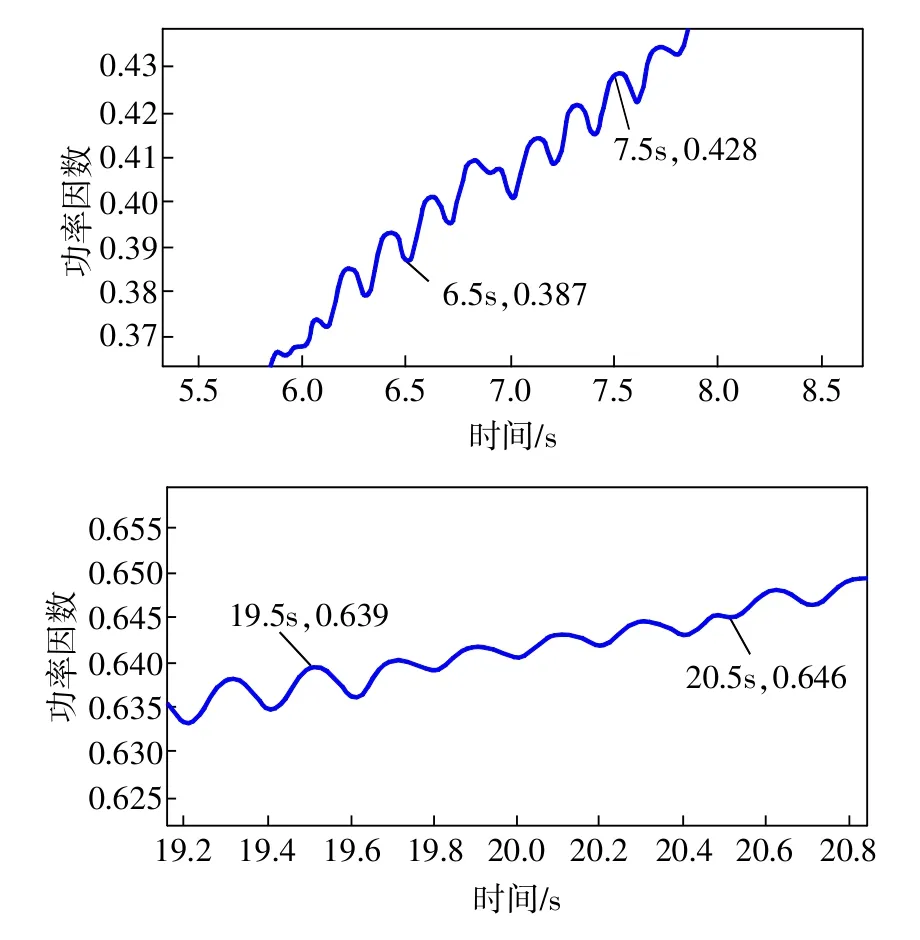
图6　局部放大后的功率因数曲线

表4　功率因数测量值和计算值对比

表5　功率因数测量误差

4　结束语

基于谐波小波的优良特性和功率因数定义，本文提出了测量工频功率因数的广义谐波小波变换算法，建立了其数学模型，并通过仿真与实验进行对比验证。仿真分析和实验结果表明：与其他功率因数测量算法相比，广义谐波小波的零相移、采样频率与采样点数不变的特性在提取工频功率因数上具有明显优势，算法运算速度快、准确度高（实测误差＜3.5%），具有良好的工程实用价值。

参考文献

[1]陈文光，唐少农.功率因数的概念及测试方法探讨[J].电气电子教学学报，2002，24（5）：73-75.

[2]刘学会，张伟，王永刚，等.非正弦电流电网的功率因数及其测量[J].电测与仪表，2004，41（457）：23-25.

[3]张进高，卢琴芬，王利，等.基于FFT的直线电机地铁牵引电机功率因数角测量[J].浙江大学学报（工学版），2012，46（11）：1981-1984.

[4]张庆新，王凤翔.异步电机的功率因数检测及其控制[J].电工技术杂志，2001（10）：44-46.

[5]刘艳梅.有功功率的最佳起始角采样与小波包测量方法研究[D].重庆：重庆大学，2013.

[6]胡家华，徐鹏，郑昌雨，等.异步电机功率因数的数字测量[J].电机技术，2013（6）：44-50.

[7] KULKARNI H H，MAHARASHTRA D G. DFT and wavelet based smart virtual measurement and assessment of harmonics in distribution sector [J]. Smart Innovation Systems and Technologies，2015（31）：275-284.

[8] TARABINI M，GIRONACCI A，PANZERI R，et al. Signal processing techniques for the identification of wheels imbalanceinpresence of disturbances [J]. Mechanisms and Machine Science，2015（21）：475-483.

[9]夏洪瑞，葛川庆.谐波小波滤波功效分析[J].勘探地球物理进展，2007，30（3）：168-177.

[10]张方彦.谐波小波在电力系统(间)谐波检测中的应用研究[D].吉林：东北电力大学，2008.

[11] NEWLAND D E. Harmonic wavelet analysis[J]. Proceeding: Mathematical and Physical Sciences，1993，443（1917）：203-225.

[12] HAIGH S K，TEYMUR B，MADABHUSHI S P G，et al. Applications of wavelet analysis to the investigation of the dynamic behaviour of geotechnical structures[J]. Soil Dynamics and Earthquake Engineering，2002（22）：995-1005.

（编辑：莫婕）

Measuring algorithm for power frequency factor based on general harmonic wavelet

ZHANG Yuan1，2，WANG Nan3
（1. School of Electronic Information and Electric Engineering，Shanghai Jiao Tong University，Shanghai 200240，China；2. Engineering Department of 705 Research Institute，CSIC，Shanghai 200245，China；3. School of Mechanical Engineering，Shanxi University of Technology，Hanzhong 723001，China）

Abstract:To solve the existing problems of traditional power factor measuring methods, general harmonic wavelet is proposed to measure the power factors based on the features of the general harmonic wavelet, i.e., zero phase-shift, the sampling frequency and points of data series that remain unchanged at different decomposition scales, as well as the definition of power factors. The operating procedure of the algorithm is as follows: First, the discretized voltage and current signals are extracted in power frequency; Second, the results obtained are reconstructed; third, it is measured with the definition of power factors. Besides, a mathematical model is established for simulation analysis. Then, the algorithm is verified through hydraulic system tests and the power frequency factor is obtained. The analyzing results have shown that the algorithm is fast and precise less than 3.5% in terms of measuring errors compared with other algorithms (especially orthogonal wavelet), it can be applied in some engineering fields.

Keywords:general harmonic wavelet；power factor；FFT；Mallat algorithm

作者简介：张媛（1989-），女，助理工程师，硕士，研究方向为现代数字信号处理。

基金项目：陕西省教育厅专项科研计划资助项目（14JK1142）；中船重工705研究所总工程师基金项目（CX_1416）；陕西理工学院院士工作站建设项目（fckt201510）

收稿日期：2015-08-10；收到修改稿日期：2015-09-15

doi：10.11857/j.issn.1674-5124.2016.01.004

文献标志码：A

文章编号：1674-5124（2016）01-0016-05