基于EFG方法的PBX炸药圆弧巴西实验的数值模拟

崔云霄，陈鹏万，戴开达，王雷元，刘龑龙

(1. 北京理工大学爆炸科学与技术国家重点实验室，北京100081； 2. 西北核技术研究所，陕西西安710024)



基于EFG方法的PBX炸药圆弧巴西实验的数值模拟

崔云霄1,2，陈鹏万1，戴开达1，王雷元2，刘龑龙1

(1. 北京理工大学爆炸科学与技术国家重点实验室，北京100081； 2. 西北核技术研究所，陕西西安710024)

摘要：为了对准静态圆弧巴西实验过程中PBX试样的裂纹形成和扩展过程进行模拟，基于EFG方法和内聚力模型，利用LS-DYNA软件的隐式分析模拟计算了实验过程。结果表明，计算结果和文献报道的实验结果吻合较好，证明了该方法的可行性；采用线性内聚力模型可较好地描述PBX炸药的断裂过程，PBX试样的起裂发生在压缩载荷达到峰值后，随着压头的进一步压缩，试样中心的裂纹沿直径向压头方向扩展。

关键词：固体力学；圆弧巴西实验；EFG方法；内聚力模型；PBX；LS-DYNA软件

引言

高聚物黏结炸药(PBX)是由HMX炸药、聚合物和添加剂组成的一种固体高能炸药。研究其损伤断裂性能，对于热点点火预测、装药安全性评估具有重要意义[1]。在外部载荷作用下，PBX炸药内部可能产生炸药颗粒脱粘、微裂纹演化等宏观或细观损伤，使力学性能劣化，甚至会影响“热点”的形成。

目前，PBX的损伤断裂性能研究主要集中于拉伸断裂，如直接拉伸实验、巴西实验、三点弯曲实验等。相对而言，巴西实验的试样制备简单、所需材料少、方便快捷[2]。传统巴西实验在实验过程中加载接触点容易产生应力集中，使得该位置可能提前发生破坏，影响测试结果的有效性[3]。Mellor等[4-7]采用圆弧巴西实验，通过把压头接触面改进为弧形，增大了接触面，提高了实验结果的可重复性。由于PBX炸药兼有黏弹性和准脆性的力学特征，准确描述其力学响应及断裂特性比较困难。黄涛[8]采用流形元法对PBX炸药的损伤破坏过程进行了数值模拟，将建立在实验测量上的弹性损伤模型引入到流形元程序，通过有预制裂纹和无预制裂纹两种条件下的巴西实验，探讨了损伤对裂纹扩展过程的影响。赵四海[9]利用Visco-SCRAM模型计算了圆弧巴西实验中PBX炸药圆盘试样的力学响应，结果显示，在圆盘与圆弧垫块接触位置损伤变量较大，损伤呈哑铃分布。

无网格迦辽金方法(EFG)是由Belytschko T提出的一种无网格数值计算方法[10]，具有较好的协调性和稳定性，在动力有限元软件LS-DYNA中可进行基于EFG方法的模拟分析。本研究基于结合内聚力模型的EFG断裂模拟方法，计算了准静态加载圆弧巴西实验中PBX炸药的力学响应和断裂行为，以期为含能材料损伤破坏行为的研究提供参考。

1裂纹模拟方法

1.1EFG方法

EFG方法的基本思想是：计算域Ω内的函数u(X)，可根据该域内的若干已知点，由最小二乘法构造其近似函数，即

(1)

式中：p(X)为基函数；a(X)为与X相关的系数，由二次方程式J(X)求极小值得到

(2)

式中：wi(X)为非负的权函数，其有一个影响范围，超出影响范围时，权函数为0。

新版LS-DYNA软件中引入了结合内聚力模型的EFG断裂扩展算法[11]，借助可视判据，程序自动将内聚力模型定义在单元边缘。起裂判据采用最大拉应力判据，裂纹张开过程采用内聚力模型描述。使用该方法模拟计算材料或结构的断裂问题，不需要在材料或结构中预置裂纹，对于三维模型，只要建立四面体单元作为背景网格。

1.2内聚力模型

内聚力模型本质上是一种唯象模型，其张力位移关系是对裂纹前端断裂过程区的一种连续介质损伤力学描述。当达到最大应力时，内聚力区域开始起裂，而当达到临界张开位移时，单元删除，物理裂纹出现，此时，内聚力作功等于临界能量释放速率。基于EFG方法模拟材料或结构的断裂破坏，内聚力模型采用的是Tvergaard-Hutchinson模型[12]，该模型是三线性(梯形)张力位移关系，如图1所示。

图1　Tvergaard-Hutchinson模型的梯形张力位移关系Fig.1　Trapezoid relation between the traction anddisplacement of Tvergaard-Hutchinson model

Tvergaard-Hutchinson模型使用一个无量纲张开位移λ来度量法向断裂(λ3)和切向断裂(λ1，λ2)相对位移之间的相互作用

(3)

式中：NLS和TLS分别为界面法向和切向的最大位移张开值；<>为McCauley括号，用来区分拉伸(λ3≥0)和压缩(λ3<0)。

张力的控制方程为：

(4)

(5)

在数值模拟中，除了最大应力值及临界张开位移作为参数外，还要选择给出δ1和δ2。研究表明[13]，对于脆性材料，线性内聚力模型比较合适，因此将δ1和δ2设为0，Tvergaard-Hutchinson模型的张力位移关系退化为线性关系。

2圆弧巴西实验及计算模型

实验材料为PBX9501，其配方(质量分数)为：HMX 95%、Estane 2.5%、NP 2.5%，圆盘尺寸为Φ25.4mm×6.35mm，常曲率垫块与圆盘的半径比为1.25，MTS材料试验机常速率加载，顶部圆弧压头的移动速率为0.5mm/min，实验装置如图2所示[6]。根据实验装置，建立三维全尺寸计算模型。

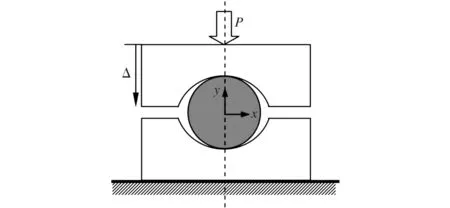
图2　实验装置示意图Fig.2　Schematic diagram of the experimental apparatus

采用四面体单元对巴西圆盘试样进行网格划分，单元总数为97344个，节点总数为18729个，划分后的模型如图3所示。采用六面体单元对两个圆弧压头进行网格划分，单元总数为9680个，节点总数为12222个；上压头施加位移边界，模拟压头运动，下压头施加固定边界，压头与试样之间采用自动面面接触。

图3　巴西圆盘试样的网格划分模型Fig.3　FEM mesh model of Brazilian disk specimen

为了模拟实验采用的常速率加载，显式分析需要较长的时间，因而采用隐式分析。压头为钢材料，采用弹性本构，密度为7850kg/m3，弹性模量为211GPa，泊松比为0.3。对于PBX炸药，断裂前将其力学行为近似描述为弹性，材料参数为：密度1.829g/cm3，弹性模量2.8GPa，泊松比0.3。达到起裂判据后，结合内聚力模型描述其内部裂纹的形成。参考PBX9501的抗拉强度，内聚拉伸强度取1.8MPa。选定内聚拉伸强度后，根据断裂能采用线性内聚力模型估算临界张开位移。根据文献[14]，其断裂韧性约0.29MPa·m1/2，平面应变下断裂能与断裂韧性的关系为

(6)

式中：KIC为断裂韧性；v为泊松比；E为弹性模量。

因此，由式(6)换算得到断裂能，并根据式(5)可以确定出临界张开位移。在此基础上经过试算，采用的PBX材料的临界张开位移为0.032mm。选择过大的临界张开位移，试样在2%的直径变化下都不发生断裂；而选择过小的临界张开位移，试样会提前破坏，且网格发生畸变。

3计算结果与讨论

模拟得到压头施加的压缩载荷随试样直径变化的曲线见图4，载荷(p)利用试样的厚度(w)和半径(R)归一化。图4中还给出了试样中心的裂纹张开位移曲线，该曲线是根据试样中心位置单元两侧节点的x方向位移曲线相减得到的，裂纹张开位移(δ)以试样直径(D)归一化。

图4中A、B、C和D四个圆圈分别对应40.65、44.40、45.25和46.45s四个时刻，其中A点为压缩载荷达到峰值前的一个时刻，试样尚处于弹性变形，直径变化约1.3%，内部微裂纹开始演化，裂纹张开位移曲线的斜率已发生变化；B点为压缩载荷达到峰值11.06MPa的时刻；C点为压缩载荷开始下降而整体变形仍在增加的时刻，材料发生软化。由图4可见，裂纹张开位移曲线的斜率在B点和C点之间发生突变，如图4中的实心原点，对应无量纲位移为1.48%，即45.1s时，试样起裂。实际实验中，采用1N的载荷预压，计算中未考虑预压过程，而在无量纲位移达到0.1%前(约3s)，模拟得到压头载荷无较大变化，扣除该部分时间，则起裂时间为42.1s，与基于DIC方法测试得到的起裂时间37.4s较为接近[6]。D点为压缩载荷下降到局部最低值的时刻，随着压头位移的增加，载荷将开始回升。起裂后，裂纹张开位移快速增加，并开始沿直径向压头方向扩展。

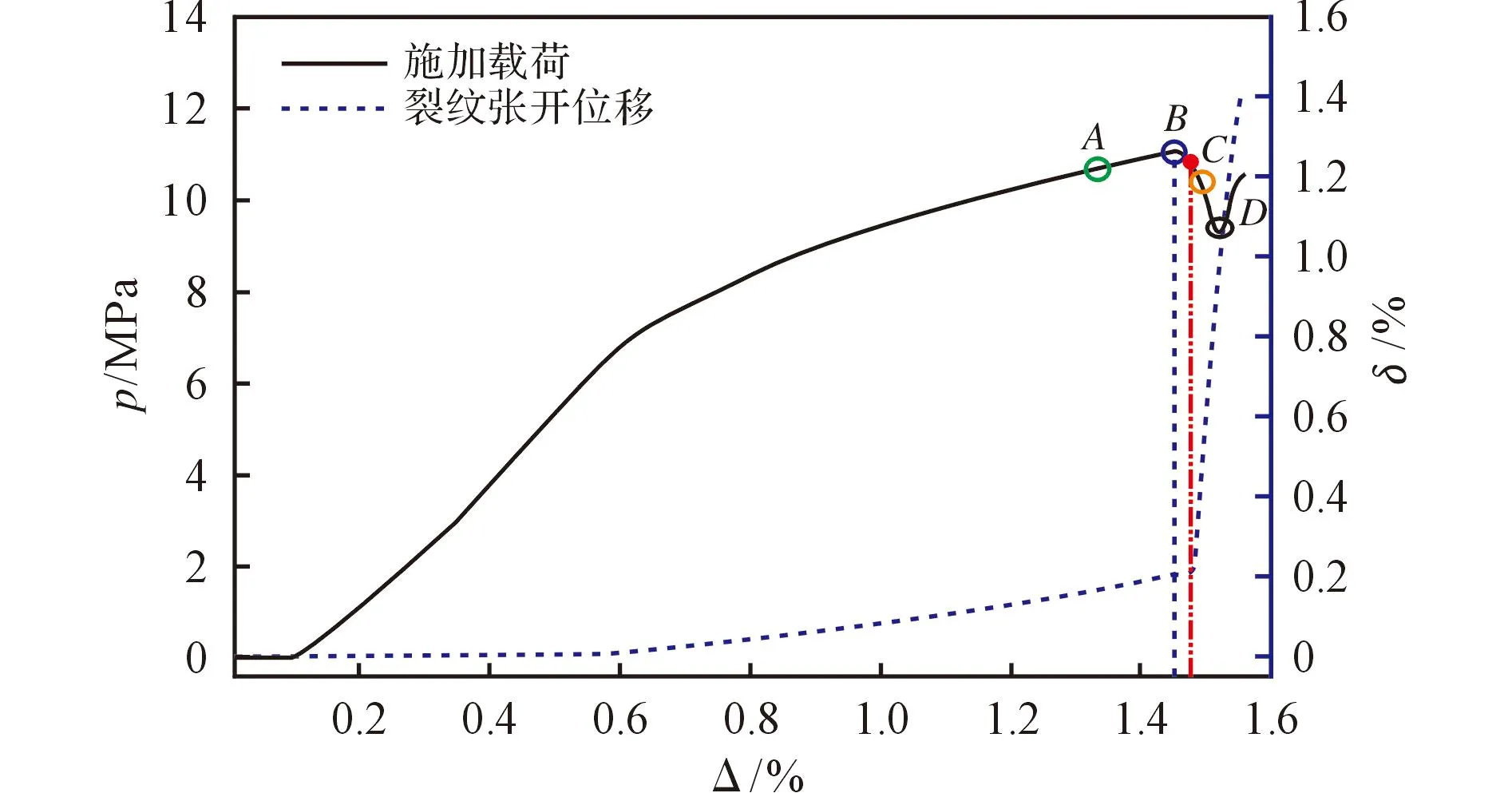
图4　施加载荷随PBX试样直径变化的曲线Fig.4　Curves of applied load vs. variation of diameterof PBX sample from simulation

试样在不同时刻沿x方向的位移云图见图5，分别对应图4的A、B、C、D时刻。

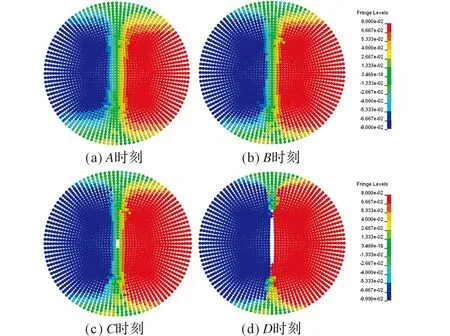
图5　不同时刻PBX试样x方向的位移云图Fig.5　Selected contour plots of x-displacement of PBXsample from simulation at different time

从图5可以看出，C时刻在试样的中心附近出现宏观裂纹，到D时刻后，裂纹已向两端扩展，且裂纹宽度增加。采用DIC方法得到试样在C时刻和D时刻沿x方向位移云图见图6[6]。

图6　DIC方法测得PBX试样x方向的位移云图Fig.6　Selected contour plots of x-displacement ofPBX sample from DIC measurement

从图6可以看出，数值模拟得到的位移云图与采用DIC方法获取的位移云图具有相似的分布，试样沿直径方向存在一条宏观裂纹。在C时刻，模拟得到x方向的位移峰值比DIC方法得到的结果稍偏大。

试样在不同时刻x方向的应变云图见图7，分别对应图4的A、B、C、D时刻。

图7　不同时刻PBX试样x方向的应变云图Fig.8　Selected contour plots of x-strain of PBXsample from simulation at different time

由图7可以看出，在圆盘的中心周围有一个应变等值线圈，位于等值线圈内的单元处于拉伸状态。B时刻试样中心出现局部高应变区；C时刻试样中心出现宏观裂纹，裂纹周围还存在高应变区；D时刻裂纹向两端扩展，试样内部的应变能释放，裂纹附近的拉应变减小，裂纹尖端附近仍存在应变集中区。

采用DIC方法计算得到起裂时刻和裂纹扩展过程x方向的应变云图见图8[6]。试样在不同时刻y方向的位移云图见图9。

对比图7和图8可知，模拟得到的x方向的应变结果和实验结果较一致，应变峰值约为6%，说明基于EFG的断裂模拟方法对PBX材料断裂破坏过程进行模拟分析是可行的。

图8　DIC方法测得PBX试样x方向的应变云图Fig.8　Selected contour plots of x-strain of PBXsample from DIC measurement

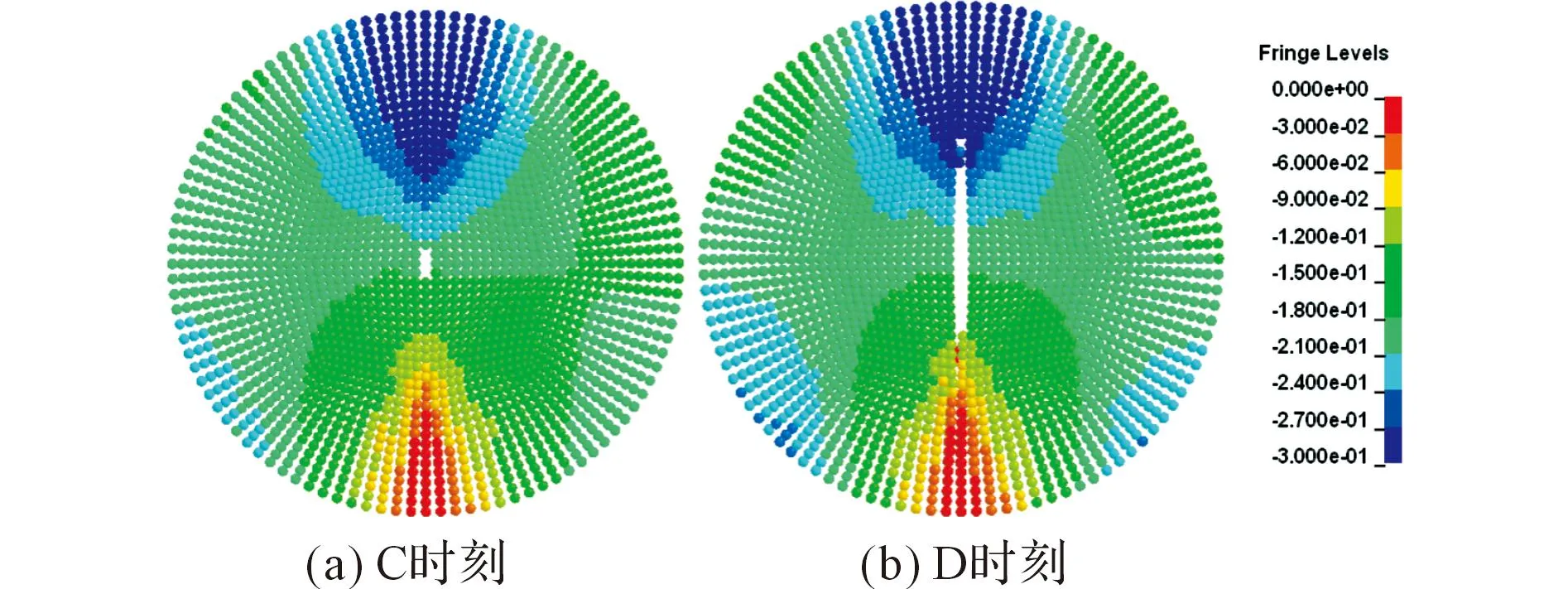
图9　不同时刻试样y方向的位移云图Fig.9　Selected contour plots of y-strain of samplefrom simulation at different time

由图9可以看出，试样中与压头接触的部位位移峰值约0.3mm，没有出现过早破坏，说明采用圆弧压头后改善了标准巴西实验中试样端头的应力集中问题。

从数值模拟的结果看，在施加的压缩载荷达到峰值时，PBX炸药并未发生宏观断裂，而是在紧跟载荷峰值之后，圆盘试样的中心出现裂纹，与实验结果一致。随着压头位移的增加，裂纹沿试样直径向两端扩展。需要指出的是，目前该计算还存在不稳定的情况，其方法还在发展之中。

4结论

(1)利用LS-DYNA程序的EFG方法，结合内聚力模型，对PBX圆弧巴西实验进行了数值模拟，再现了准静态压缩下PBX圆盘的裂纹萌生及扩展的过程，计算得到的变形场分布与实验结果符合较好。

(2)采用线性演化内聚力模型及合适的参数可以较好地描述PBX炸药断裂破坏过程中的能量耗散行为，根据模拟计算结果可知，试样起裂发生于压缩载荷达到峰值之后。

参考文献：

[1]陈鹏万, 黄风雷. 含能材料损伤理论及应用[M]. 北京: 北京理工大学出版社, 2006.

CHEN Peng-wan, HUANG Feng-lei. Damage Theory and Application of Energetic Materials[M]. Beijing: Beijing Institute of Technology Press, 2006.

[2]Johnson H D. Mechanical properties of high explosives, MHSMP-74-19[R]. Amarillo: Mason and Hanger-silas Mason Co., Inc., 1974．

[3]庞海燕, 李明, 温茂萍, 等. PBX巴西试验与直接拉伸试验的比较[J]. 火炸药学报, 2011, 34(1):42-44.

PANG Hai-yan, LI Ming, WEN Mao-ping, et al. Comparison on the Brazilian test and tension test of the PBX[J]. Chinese Journal of Explosives and Propellants, 2011, 34(1):42-44.

[4]Mellor M, Hawkes I. Measurement of tensile strength by diametric compression of discs and annuli[J]. Eng Geol, 1971, 5:173-225.

[5]陈鹏万, 黄风雷, 张瑜. 用巴西实验评价炸药的力学性能[J].兵工学报,2001,22(4): 533-537.

CHEN Peng-wan, HUANG Feng-lei, ZHANG Yu. Brazilian test and its application in the study of the mechanical properties of explosives[J]. Acta Armamentarii, 2001,22(4): 533-537.

[6]Liu C, Thompson D G, Lovatoy M L, et al. Macroscopic crack formation and extension in pristine and artificially aged PBX 9501[C]∥Proceedings of the 14th International Detonation Symposium. Idaho: Office of Naval Research, 2010.

[7]陈科全, 蓝林钢, 路中华, 等. 含预制缺陷PBX炸药的力学性能及破坏形式[J]. 火炸药学报, 2015, 38(5):51-53.

CHEN Ke-quan, LAN Lin-gang, LU Zhong-hua, et al. Mechanical properties and failure modes of PBX explosives with different prefabricated defects[J]. Chinese Journal of Explosives and Propellants, 2015, 38(5):51-53.

[8]黄涛. 高聚物粘结炸药损伤破坏的流形元法模拟研究[D]. 北京：北京理工大学，2006.

HUANG Tao. Numerical simulation of damage and fracture of polymer bonded explosives by manifold method[D]. Beijing: Beijing Institute of Technology, 2006.

[9]赵四海. 用粘弹性统计裂纹模型模拟高能炸药的力学响应和非冲击点火[D]. 长沙: 国防科技大学, 2011.

ZHAO Si-hai. A viscoelastic statistic crack constitutive model for mechanical response and the Non-shock ignition of high explosives[D]. Changsha: National University of Defense Technology, 2011.

[10]Belytschko T, Lu Y Y, Gu L. Crack propagation by element-free galerkin methods[J]. Engineering Fracture Mechanics, 1995, 51: 295-315.

[11]GUO Yong, Wu C T. XFEM and EFG cohesive fracture analysis for brittle and semi-brittle materials[C]∥11th International LS-DYNA Users Conference. Livermore: Livermore Software Technology Corp, 2010, 421-432.

[12]Tvergaard V, Hutchinson J W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids, 1992, 40(6): 1377-1397.

[13]Xu X P, Needleman A. Analysis of ductile crack growth by means of a cohesive damage model[J]. International Journal of Fracture, 1996, 81(2): 99-112.

[14]LIU Cheng, Cady C M, Rae P J, et al. On the quantitative measurement of fracture toughness in high explosive and mock materials[C]∥Proceedings of the 14th International Detonation Symposium. Idaho: Office of Naval Research, 2010.

Numerical Simulation of PBX under Circular Anvil Brazilian Test Based on EFG Method

CUI Yun-xiao1,2，CHEN Peng-wan1，DAI Kai-da1，WANG Lei-yuan2，LIU Yuan-long1

(1. State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology, Beijing 100081， China;2.Northwest Institute of Nuclear Technology，Xi′an 710024，China)

Abstract:To simulate the crack formation and extension process of PBX sample in the quasi-static circular anvil Brazilian test, based on EFG method and cohesive model, the experimental process was calculated by implicit analysis and simulation of LS-DYNA software. The results show that the calculated results are in good agreement with reported experimental ones in literature, proving the feasibility of the method. The fracture process of PBX can be well described by linear cohesive model. The crack initiation of PBX sample occurs after the compression load reaches the peak value, and with the further compression of compression anvil, the crack of the specimen center extends along the diameter direction to the anvil.

Keywords:solid mechanics；circular anvil Brazilian test；EFG method；cohesive model；PBX；LS-DYNA software

中图分类号：TJ55; O346

文献标志码：A

文章编号：1007-7812(2016)01-0034-05

作者简介:崔云霄(1980-)，男，博士研究生，从事装药安全性和点火机理研究。E-mail:yunxiaocui@163.com

基金项目:国家自然科学基金资助(No.11202027，No.11221202，No.U1330202)

收稿日期:2015-08-29；修回日期:2016-01-04

DOI：10.14077/j.issn.1007-7812.2016.01.005