基于畦灌灌水效果的土壤入渗参数预测精度控制研究

雷国庆，樊贵盛

(太原理工大学，太原 030024)

畦灌作为我国主要的地面灌溉方式之一，其灌水效果受畦长、单宽流量、灌水时间、土壤入渗参数、田面坡度及糙率等因素影响，其中土壤入渗参数对其影响显著[1]。在畦灌灌水过程中，土壤水分入渗特性直接影响着田面水流的推进及消退过程，直接对灌水后土壤水分的分布造成影响，灌水效果可能出现显著差异。因此，合理选取土壤入渗参数对畦灌灌水效果改善具有重要意义。然而，由于土壤入渗能力空间变异性的存在，区域尺度上的入渗参数获取较为困难，基于此，学者们试图建立关于入渗参数的土壤传递函数[2]，利用较易获取的土壤理化参数对土壤入渗参数进行预测，其中曹崇文[3]以不同深度上的土壤密度、含水率、质地、有机质含量等为已知参数，试图建立线性、非线性和人工神经网络等模型对土壤入渗参数进行预测。然而由于不同预测模型得到的预测精度有较大差异，预测精度的差异是否会对畦灌灌水效果产生影响，产生的影响是否可被接受尚缺乏有效验证。

在地面灌溉领域，土壤入渗参数的精度控制需建立在灌水效果指标对入渗参数变化敏感程度的基础上。学者们在入渗参数空间变异对灌水质量影响方面作了较多研究，其中朱艳等[4]选用两参数Kostiakov模型，认为灌水均匀度和灌水效率对入渗参数k、α的响应关系均为单峰二次曲线，并且入渗参数k稳定区间较α大；王维汉等[5]基于稳健设计理论，通过正交试验进行敏感性分析，认为对灌水质量影响较大的因素依次为单宽流量q、入渗指数α、入渗系数k。但如何利用灌水效果对入渗参数变异的敏感性，建立土壤入渗参数精度控制模型尚未得到有效解决。在前人研究的基础上，本文以汾东灌区北长寿的灌水试验为背景，对试验点的灌水技术参数组合进行多目标模糊优化[6]，在此基础上，以优化灌水技术参数为固定参数，将土壤入渗参数k、α和f0进行不同程度的偏离，利用地面灌溉模拟软件WinSRFR[7]对不同入渗特性下的畦灌灌水效果进行模拟，通过灌水效果敏感性分析结合灰色关联理论[8]，以期建立土壤入渗参数预测精度控制模型。

1 畦灌灌水模型及评价指标

1.1 土壤水分入渗模型

为有效地对土壤入渗性能进行表征，选用应用范围最广的Kostiakov三参数入渗经验模型[9]。该模型形式简单、拟合精度高，其表达式如下：

Z=ktα+f0t

(1)

式中：Z为累积入渗水深，mm；k为土壤入渗系数，mm/s；t为入渗时间，s；α为入渗指数；f0为常数项，mm/s。

由式(1)可知，土壤入渗参数k、α、f0反映土壤的入渗特性，不同的入渗参数组合土壤入渗能力不同 。其中当t→0时，k=Z，表示土壤在初始时刻的入渗能力；在水分入渗过程中，入渗指数α表征土壤水分入渗能力的衰减速度，反映土壤水分入渗特性曲线的饱满程度；而t→∞时，f0=Z′,即入渗参数f0指土壤在达到饱和后的稳定入渗速率。

1.2 田面水流运动模型

对于水平畦田，圣维南动量方程中的加速项和惯性项均可考虑不计，田面水流运动选用零惯量模型[10]进行模拟：

(2)

式中：A为田面水流的断面面积，m2；Q为田面水流流量,m3/s；x为沿畦长方向距畦首的距离，m；H为累积入渗水深，m；S0为田面坡度；Sf为阻力坡度。

1.3 畦灌灌水效果评价指标

对畦灌灌水效果评价，目前应用最为广泛的灌水效果评价指标包括灌水效率Ea、储水效率Es和灌水均匀度Du[11]。其中Ea为灌水效率，从节水的角度考虑，用来评价灌溉水的利用效率；Es为储水效率，与作物的产量相关，反映某次灌水后计划灌水量的满足程度；Du为灌水均匀度，指某次灌水后土壤水分入渗深度沿畦田纵向分布的均匀程度，考虑整个畦田的灌水质量。三者的计算公式如下：

(3)

式中：Dz为某次灌水后储存于土壤计划湿润层的平均深度，mm；Dapp为灌入田间的平均灌水深度，mm；Ddp为灌水过程中深层渗漏的平均深度，mm；Dro为畦田平均弃水深度，mm；Dreq为田间计划灌水深度，mm；Dlq为沿畦长方向上土壤受水最少的1/4段内的平均入渗水深，mm；Dinf为畦田田块上的平均入渗水深，mm。

2 灌水技术参数组合优化

2.1 试验点基本灌水资料

试验点位于汾东灌区北长寿，以试验麦田为代表，根据试验点的地形条件、田间工程规格、土壤状况以及实际灌水制度，确定畦田长度L和单宽流量q，具体范围见表1。试验点的土壤入渗参数(α，k，f0)、田面坡度i、田间糙率值n选取试验点各测点的平均值，取值见表1。计划灌水深度由土壤的凋萎系数和田间持水量决定，本文选用90 mm。

表1 汾东灌区北长寿试验点基本灌水资料

2.2 灌水技术参数的多目标模糊优化

本文以灌水效率Ea、储水效率Es和灌水均匀度Du为目标函数，畦长L、单宽流量q和灌水时间t为决策变量，建立多目标优化模型：

(4)

式中：G1为畦灌灌水效率目标函数；L为畦田长度，m；q为入畦单宽流量,L/(s·m)；t为灌水时间，min；G2为储水效率目标函数；G3为灌水均匀度目标函数；Lmax、Lmin分别为畦田最大、最小长度；qmax、qmin分别为允许入畦最大、最小单宽流量，见表1。

利用WinSRFR对不同灌水技术参数组合下的灌水效果进行模拟，将模拟结果进行回归分析，确定目标函数形式，分别先在单目标条件下对目标函数进行优化，然后根据目标函数的模糊性，引入线性隶属度函数，根据实际灌水经验确定各单目标优化结果的伸缩指标，按照最大隶属度原则，将多目标优化问题转化为一个单目标非线性优化问题，从而得出最优灌水技术参数组合，本文选取畦长L为200 m的优化灌水技术参数组合：L=200 m，q=3.2 L/(s·m)，t=93 min，此条件下的灌水效果为：Ea=96.4%，Es=95.56%，Du=89.94%。

3 土壤入渗参数预测精度控制

为实现基于畦灌灌水效果的土壤入渗参数预测精度模型，本文在优化灌水条件下，将土壤入渗参数k、α和f0进行不同程度的偏离，分析灌水效果指标的敏感响应程度，在此基础上，对各灌水效果指标与入渗参数间的灰色关联度进行分析，并利用灰色关联系数确定入渗参数k、α、f0的预测精度对灌水效果指标的影响权重，通过对畦灌灌水效果指标的误差进行约束，实现土壤入渗参数的预测精度控制。

3.1 灌水效果指标对入渗参数的敏感性分析

为分析灌水效果指标对入渗参数变化的敏感响应程度，根据实际入渗参数的变异情况，以及土壤传递函数中入渗参数常见的预测精度大小，考虑以试验点实测入渗参数k、α、f0为基准，进行上下一定程度的偏离(以5%为步长，上下最大偏离为基准的30%)，分析在不同入渗参数条件下灌水效果指标的变化程度(以较基准条件下灌水效果指标的相对误差ε表示) ，见图1。

由图1可知，各灌水效果指标对入渗参数k、α、f0偏离的敏感程度不同，灌水效率Ea和储水效率Es的敏感程度相当，对入渗参数变化反应相对较小，即使入渗参数的偏离度达30%时，Ea、Es的相对误差也控制在5%以下(此处暂不考虑各入渗参数偏离的综合影响)。而灌水均匀度Du对入渗参数变化较为敏感，当入渗参数k、f0的偏离程度达15%左右时，其相对误差可达5%左右；当入渗参数k、f0的偏离程度达30%左右时，Du的相对误差向10%逼近。

图1 土壤入渗参数k、α、f0偏离对灌水效果的影响

各入渗参数的变化对灌水效果的影响大小也不同，入渗参数k、f0变化对灌水效果的影响明显强于参数α的影响。入渗参数k、f0偏离15%左右，Ea、Es相对误差接近2%，Du相对误差接近5%，而入渗参数α偏离30%，Ea相对误差未达1%，Es相对误差未达1.5%，Du相对误差也未达3%。

3.2 灌水效果指标与土壤入渗参数的灰色关联分析

为分析各入渗参数与不同灌水效果指标间的关联程度，本文利用均匀试验设计的方法，选择U*13(133)均匀试验表[12]，对土壤入渗参数k、α、f0按上述不同偏离水平下的灌水效果指标进行模拟，结合WinSRFR模拟软件，模拟结果见表2。

现以表2中灌水效果评价指标灌水效率Ea、储水效率Es和灌水均匀度Du为参考序列x0(n)，n=1,2,…,13，而k、α、f0作为比较序列xi(n)，i=1,2,3，其中x0(n)、xi(n)表示x0、xi的第n个实数。

首先对各因素进行进行无量纲处理：

(5)

求差异序列：

Δ0i(n)=|y0(n)-yi(n)|

(6)

确定Δmin=minΔ0i(n)，Δmax=maxΔ0i(n)，并计算关联系数如下：

(7)

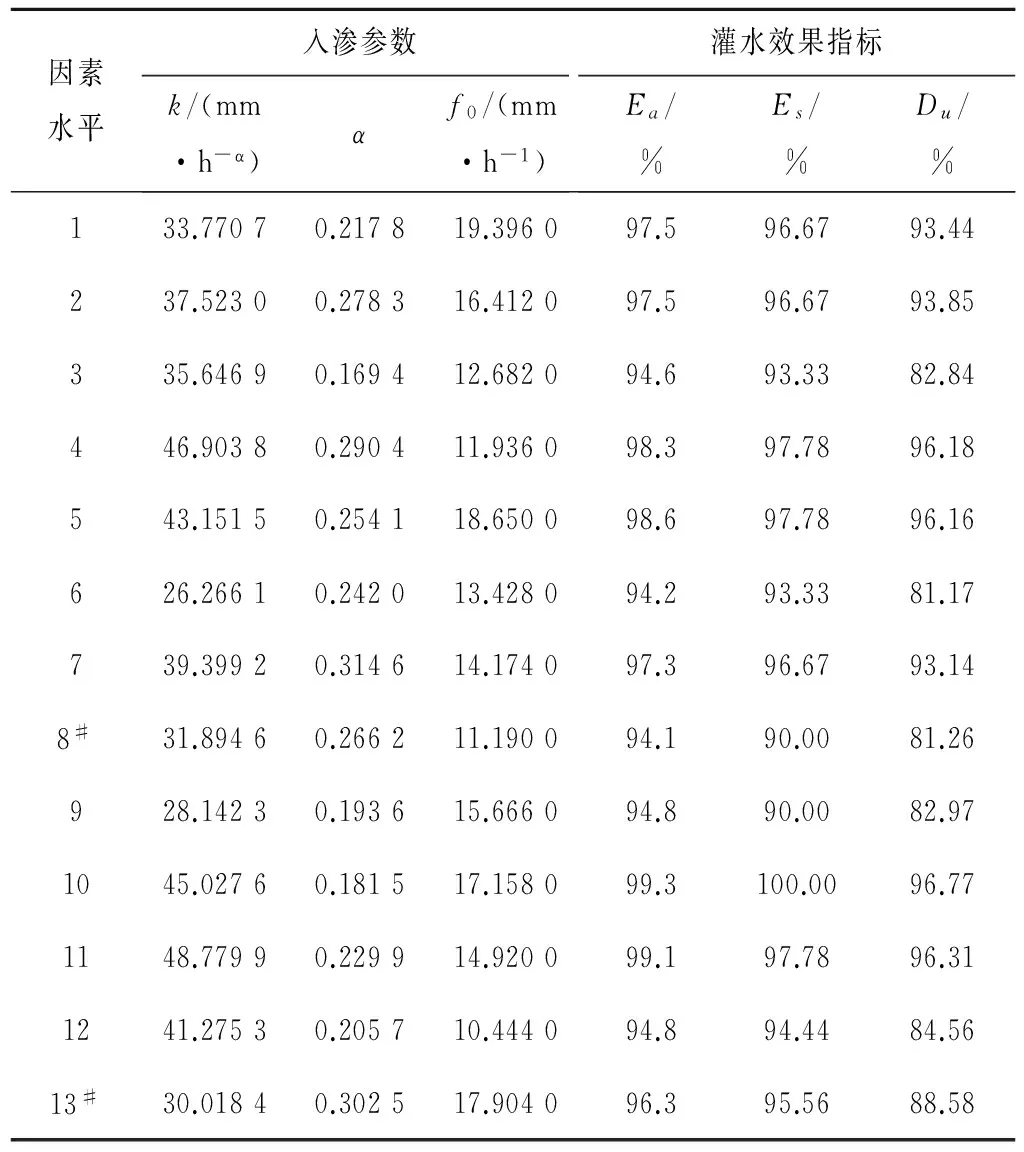
表2 均匀试验方案及模拟结果

式(7)中ρ∈(0，1]，为分辨系数，由于参考序列数据平稳，此处选用较大的分辨系数1。

则各入渗参数的关联度r0i为：

(8)

根据上述方法，可得各灌水效果指标与入渗参数间的灰色关联度，见表3。

灰色关联分析结果显示，对于灌水效果指标Ea、Es、Du而言，各入渗参数与其灰色关联程度由大到小为：k>f0>α。由此可见入渗系数k与灌水效果指标关联程度较为密切，入渗参数f0次之，入渗指数α与灌水效果指标关联性较小。

表3 均匀试验方案及模拟结果

3.3 土壤入渗参数的预测精度控制

在其他灌水技术参数一定的情况下，畦灌灌水效果的误差受土壤入渗参数k、α、f0精度的综合影响，因而要降低灌水效果误差，需全面考虑土壤入渗参数k、α、f0的精度问题。上述只分析了单因素入渗参数偏离情况下的灌水效果指标相对误差，而灌水效果指标的实际总相对误差不能由单个入渗参数偏差引起的灌水效果误差简单直接相加，基于此，本文拟考虑灌水效果指标的总误差为各入渗参数引起的灌水效果误差的加权和。根据灌水效果指标与入渗参数间的灰色关联度，引入各入渗参数偏差对灌水效果指标误差的权重系数ξ：

(9)

式中：ξi表示各入渗参数k、α、f0的偏差影响权重，i=1,2,3；r0i为各入渗参数与灌水效果指标的灰色关联度。

各入渗参数偏差的权重系数见表4。

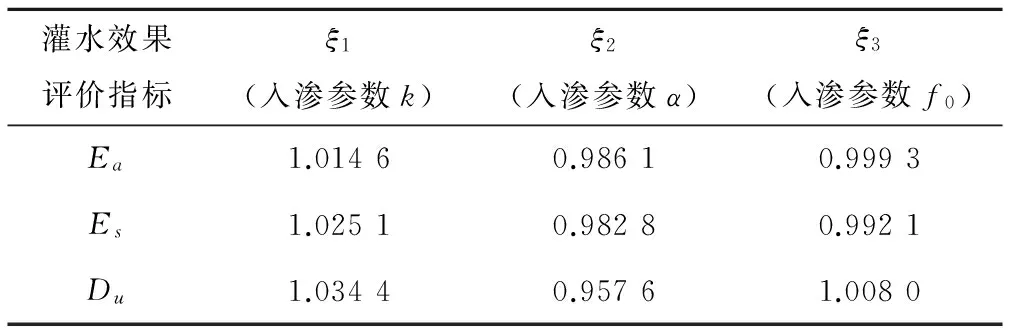
表4 各入渗参数偏差对灌水效果指标误差的影响权重

由表4可以看出，入渗参数k的权重系数略大，f0的次之，α的权重略小，结合灌水质量要求和实际灌水经验，对于灌水效率Ea和储水效率Es，其指标的大小对灌水质量的影响较大，本文考虑两指标的相对误差应控制在5%以内，而对于灌水均匀度Du而言，其对灌水质量影响相对于上述两者相对较小，本文考虑将其相对误差控制在10%以内。综上所述，建立土壤入渗参数的预测控制模型：

(10)

由式(10)可知，利用灌水效果指标对入渗参数的敏感性分析结果，结合入渗参数偏差引起的灌水效果指标总相对误差约束，即可实现入渗参数的预测精度控制。

4 结 论

(1)在优化灌水条件下，各灌水效果指标对入渗参数变化的敏感程度并不一致，土壤入渗参数的预测精度或变异情况主要对灌水均匀度Du产生影响。入渗参数k、f0变异对灌水效果指标的影响相对较大，入渗指数α的影响较小。结合文中建立的入渗参数精度控制模型，在对其进行参数预测时，建议入渗参数k、f0的预测相对误差应在20%以内，α的预测相对误差可放宽至30%。

(2)通过对入渗参数变化引起的畦灌灌水效果允许相对误差进行约束，结合灌水效果指标的敏感度分析，建立了土壤入渗参数预测精度控制模型，为关于入渗参数的土壤传递函数模型建立提供了依据。在文中的灌水条件下，权重系数的差异并不明显，但当灌水条件(单宽流量、灌水时间等)发生变化时，权重系数可能会有较明显差异。

(3)本文仅通过将各入渗参数对灌水效果指标误差进行了直接加权相加，并未考虑入渗参数对灌水效果的交叉影响，如何在考虑各入渗参数交互作用的基础上，建立土壤入渗参数的精度控制模型仍有待进一步的研究。

[1] Oyonarte N A, Mateos L. Accounting for soil variability in the evaluation of furrow irrigation[J]. Transactions of the American Society of Agricultural Engineers, 2003,46(1):85-94.

[2] 黄元仿,李韵珠. 土壤水力性质的估算——土壤转换函数[J]. 土壤学报,2002,39(4):517-523.

[3] 曹崇文.利用土壤传输函数确定入渗参数的方法研究[D].太原: 太原理工大学，2007．

[4] 朱 艳,缴锡云,王维汉,等. 畦灌土壤入渗参数的空间变异性及其对灌水质量的影响[J]. 灌溉排水报,2009,28(3):46-49.

[5] 王维汉,缴锡云,彭世彰,等. 基于稳健设计理论的畦灌质量敏感性分析[J]. 农业工程学报,2010,26(11):37-42.

[6] 刘普寅，吴孟达.模糊理论及其应用[M].长沙：国防科技大学出版社，1998：134-148.

[7] Bautista E, Clemmens A J, Strelkoff T S, et al. Analysis of surface irrigation systems with WinSRFR-Example application[J]. Agricultural Water Management,2009,96(7):1 162-1 169.

[8] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社, 2004.

[9] Kostiakov A N．On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it froma dynamic point of view for purposes of amelioration [J]．Soil Sci,1932,97(1)：17-21.

[10] 李远华，罗金耀.节水灌溉理论与技术[M].武汉：武汉大学出版社,2003：166-173.

[11] 林性粹,王 智,李援农.农田灌水质量指标的分析与评价[J].水利学报, 1996, 30(11)：74-77.

[12] 方开泰，马长兴.正交与均匀试验设计[M].北京：科学出版社，2001.