图像的能量波动对自动聚焦评价函数的影响

潘雪娟，朱尤攀，潘 超，夏丽昆，曾邦泽，罗 琳，赵德利，李泽民



图像的能量波动对自动聚焦评价函数的影响

潘雪娟1,2，朱尤攀1,2，潘 超1，夏丽昆3，曾邦泽1，罗 琳1，赵德利1，李泽民1

（1.昆明物理研究所，云南 昆明 650223；2.微光夜视技术重点实验室，陕西 西安 710065；3.陆军重庆军代局驻昆明地区军代室，云南 昆明 650223）

在基于图像处理的自动聚焦评价函数研究中发现，失效的评价函数曲线往往具有相似的形状，且与图像的均值曲线呈现相同的变化趋势。本文从评价函数数学原理角度分析了问题的原因，讨论了离焦模糊下图像能量波动对评价函数性能的影响及其处理方法。

自动聚焦；清晰度评价函数；背景干扰

0 引言

基于图像处理的自动聚焦深度法通过数字图像清晰度评价反馈搜索聚焦位置，图像清晰度评价的原理是清晰图像比模糊图像对比度高，边缘细节丰富，对应频域高频分量比重大。几乎所有的评价函数都是通过检测和加强对比度、高频分量信息[1-2]，使得聚焦图像的评价值对应评价函数的最值，实际图像由于景深、噪声干扰等原因聚焦图像评价值对应评价曲线极值且存在波动现象。由于图像数据的随机性，不同评价函数对不同图像具有不同的敏感性，用各类评价函数对不同场景的图像进行仿真分析，稳定的评价函数才能保证自动聚焦系统的性能，另一方面，分析评价失效的曲线，找到评价失败的原因，进行修正，提升算法性能也是设计自动聚焦系统的要求。

1 出现像质评价失效的几种函数分析

1）全频段积分函数：

根据离散傅里叶变换公式，为零频分量幅度，即背景幅度（函数并没有体现检测加强对比度、高频分量的设计思想，聚焦原理是清晰图像能量损失小），由于景深、运动干扰等因素影响，图像的背景幅度并不能反映离焦的极性，也不能反映聚焦状态，只有当聚焦图像均值恰好最大时函数才能正确对焦，函数性能不稳定。

2）Menmay函数

计算阈值以上图像灰度值与对应直方图值积之和，其定义为：

式中：为直方图阈值，可取第一次调焦运算时图像的平均灰度值；H为灰度级为的直方图值。Menmay函数相当于全频段积分函数进行阈值处理（不需要进行直方图统计），试图通过去除灰度值较低的像素抑制背景干扰。

3）频域能量函数：

①基于傅里叶变换变换的函数

离散傅里叶变换：

式中：、分别表示数字图像的行数和列数。

功率谱函数：

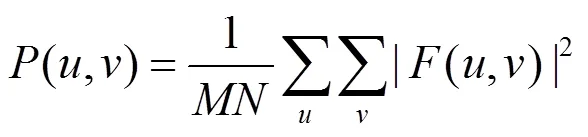
评价函数：

对图像频谱进行加权处理，更加突出地强调频谱中的高频成分：

根据帕萨瓦尔定理，式(5)频域能量计算和空域的能量计算是等价的：

式(5)为图像能量，同全频域积分函数一样，中低频分量参与计算，且函数曲线也应该与其具有相同的变化趋势。根据上面的分析，检测高频分量的评价函数抑制低频分量参与计算很重要，加权处理的评价函数，权值随着频率的增大而增大，随着频率减小而减小，在频率为零时权值也为零，既抑制了低频分量又加强了高频分量，较直接能量或功率计算的函数性能应该更稳定。

②基于离散余弦变换变换的函数

离散余弦变换：

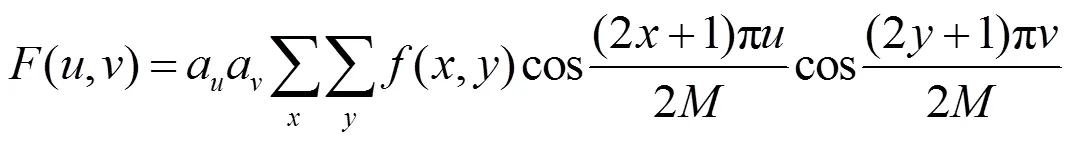
式中：

能量函数：

加权处理：

离散余弦变换同傅里叶变换一样用于频谱分析，且解决了傅里叶变换涉及复数运算的问题，评价性能跟基于傅里叶变换的函数具有基本一致的性质。

4）方差函数：

U为第幅图像平均值：

方差函数为交流能量，结合上面的分析，能量波动并不能反映聚焦状态，去除直流分量体现了抑制低频信息的思想，灰度值与图像均值的差值反映图像的对比度。在图像对比度低的情况下，图像的能量信息可能淹没对比度信息，出现评价函数曲线形状与均值曲线相似的情况。

e航海服务的具体呈现方式是MS（maritime services，之前又被叫做MSP，海事服务集），是一系列通过e航海的技术实现的标准化海上服务。通过MS的各项服务，可以实现前面所提到的e航海目标。目前，国际海事组织及国际海道测量组织正在积极推动MS的发展，并成立了一个数据协调小组（HGDM， Harmonization Group on Data Modelling）研究MS的相关事宜。

在聚焦位置附近，差值能量比较微小，很容易淹没在低频能量中，使得评价函数变化缓慢，难以精确定位聚焦点，同时抗干扰能力也比较差，对噪声比较敏感，容易出现“假焦点”。

5）Brenner函数：

Brenner函数提取图像边缘信息的方法为二阶微分，水平方向边缘检测，梯度平方处理加强梯度幅值信息。平方运算可能放大噪声干扰，造成远焦区波动大的问题，实验中使用的图像像质好，忽略噪声影响，背景能量波动可能是造成评价函数曲线波动的主要原因。

2 修正方法

1）阈值处理

阈值可以有两种作用，剔除背景信息和抑制高频噪声干扰，这与图像处理中的边缘检测、图像分割原理一致，如Menmay函数就通过阈值减小背景干扰。设置合适的阈值是需要进一步研究的问题，文献中常见的比较通用的阈值有反映图像数据波动特性的方差和标准差[4-5]，也有的文章通过实验仿真确定[6]，文献[7]提出自适应的阈值。

2）归一化处理

评价函数的设计要点是对高频分量的敏感性——检测并加强高频信息。因为自动调焦的评价搜索过程需要在序列图像中作比较，不同图像幅值波动可能会影响评价函数性能，因此，归一化处理有利于提升评价函数对数值幅度波动的抗干扰性。文献[8]采用规范化的频谱，并对规范化进行了分析说明。

3）加权处理

从检测加强高频信息角度，对边缘高频分量赋予大的权值，对低频背景信息分量赋小的权值，如式(9)对能量函数的改进，文献[9]也展示了相关性加权处理的思路。同样，权值的设置也需要深入的分析。

3 实验分析

仿真平台：联想系列电脑，CPU：Intel(R)b Core(TM) i5-4590 @ 3.3GHz，3.46GB内存，计算环境：MATLABR2012b。

仿真数据：如图1所示，每组图像都由调焦过程中“离焦-聚焦-离焦”的图像序列组成。第一组简单场景图像，背景干净、目标边缘丰富，38幅图像中第27幅最清晰，大小640×512；第2组可见光图像对比度比红外图像高、场景较复杂，45幅图像中第30幅最清晰，大小760×576；第3组制冷红外图像，主体水平边缘丰富，背景云在动，81幅图像中第41幅最清晰，大小768×576；第4组非制冷红外人物图像，对比度低，22幅图像，前面的人在第9幅图最清晰，后面的人在第17、18幅图像清晰，大小760×576。

图2充分暴露了背景能量波动对评价函数的影响，离焦区的波动基本与图像序列的均值、能量函数一致，同时看到归一化、加权和阈值处理可以有效地改善评价函数性能，而对这组图像所设的阈值对离焦区波动的抑制效果有待提升。

图像均值函数、能量函数存在波动且波动没有一致性（与场景相关），能量函数不能反映聚焦状态。分析：根据离散傅里叶变换公式，均值为零频分量幅度，即背景幅度（函数并没有体现检测加强对比度、高频分量的设计思想），由于景深、运动干扰等因素影响，图像的背景幅度并不能反映离焦的极性，也不能反映聚焦状态，只有当聚焦图像均值恰好最大时函数才能正确对焦，函数性能不稳定。出现对焦失败的评价函数曲线具有相似形状且与图像均值曲线变化趋势相同的现象，说明两点：①背景幅度波动对图像清晰度评价函数干扰很大，在评价函数设计中抑制低频分量很重要；②这些函数评价值计算时可能引入过多的中低频分量，这与检测高频分量的评价函数设计原则不符，前者相当于低通滤波（LPF），后者相当于高通滤波（HPF），LPF＝1－HPF，函数曲线可能出现与理想评价函数相反的变化趋势，如图5对非制冷红外图像的评价结果。

图1 评价函数出现与能量函数呈现相同变化趋势的典型图像

Menmay函数相当于均值函数进行阈值处理（要进行直方图统计），试图通过去除灰度值较低的像素抑制背景干扰，实验结果表明效果很差（图3显示，对对比度高的可见光图像评价失效且函数波动大），说明评价值计算时剔除低频分量的重要性。

图2 简单场景图像清晰度评价曲线

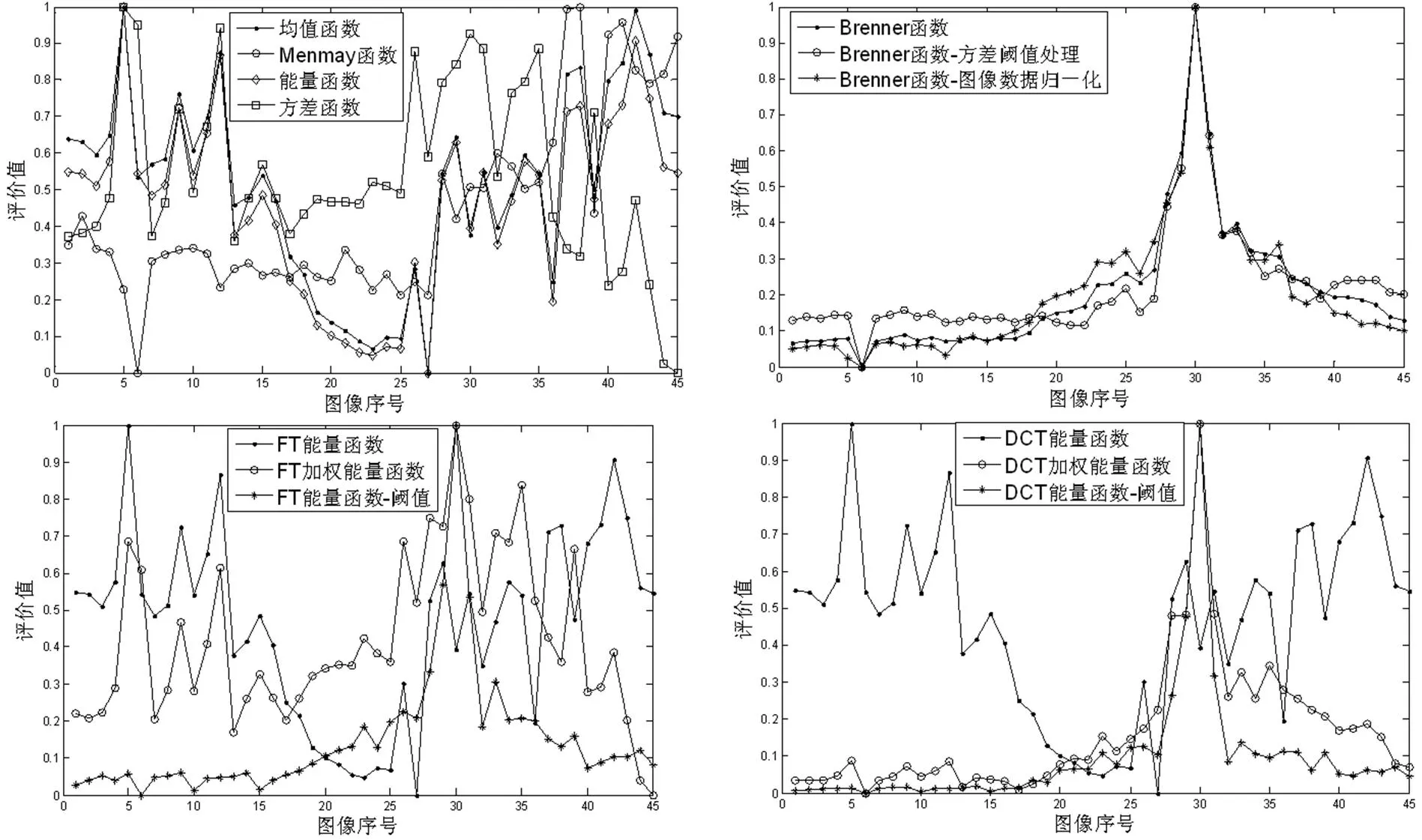
图3 可见光图像清晰度评价曲线

Fig.3 Visible light image clarity evaluation function curves

方差函数对图2所示背景干净、细节丰富的图像评价正确（见图2），对对比度高的可将光图像评价失效（见图3），与红外图像（图4、图5）一样，函数曲线呈现与均值曲线相似的形状。

Brenner函数，梯度平方处理在加强高频信息的同时可能放大背景干扰，这对图2所示背景干净、目标细节丰富的图像作用明显，离焦区评价函数曲线的波动呈现与均值函数相似的趋势，通过阈值处理、图像归一化处理来改善这种情况，实验中简单的图像归一化处理比方差阈值处理效果更好。在比较的几种函数中，基于梯度计算的Brenner函数性能较稳定，计算量也比频域函数小。

变换域的评价函数，能量函数不能正确评价图像的清晰度，加权和阈值处理后性能改善，整体而言，阈值处理性能更稳定。

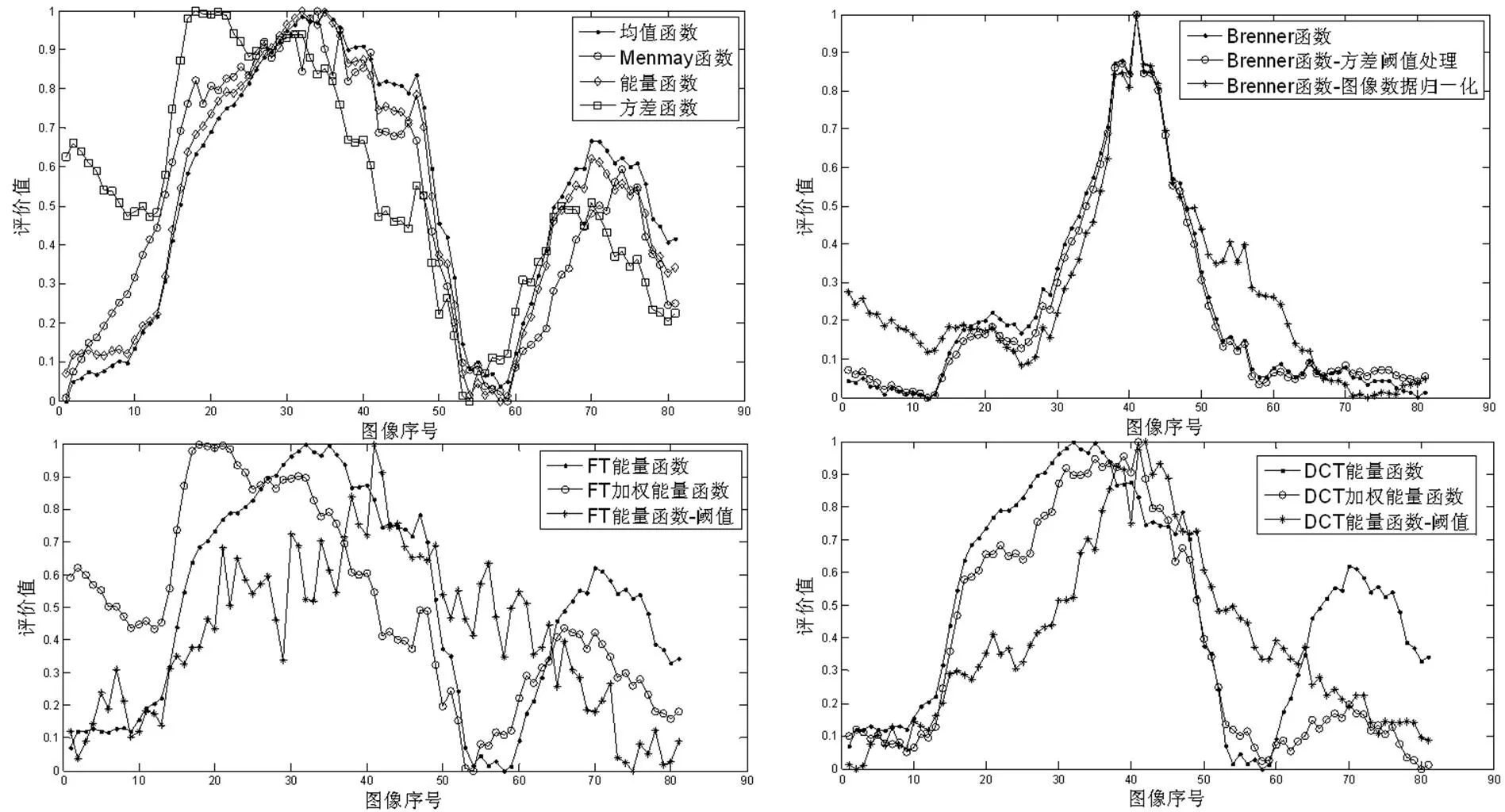
图4 制冷红外图像清晰度评价曲线

图5 非制冷红外图像清晰度评价曲线

4 结论

由于景深、背景运动等因素，图像的背景幅度（均值）和能量是波动的，图像背景和能量并不能反映聚焦位置信息。

旨在检测图像高频分量信息的评价函数，当引入过多的低中频分量参与计算时，函数曲线就会呈现与均值或能量曲线相似的变化趋势，导致对焦失败，评价算法设计中应尽量避免出现这种问题。

评价算法尽量抑制低频分量、增强高频分量信息可以提高像质评价的准确性。常见的方法有阈值处理、图像数据归一化处理、加权处理，阈值和权值的设置需要进一步的分析。

[1] Frans C A Groen, Ian T Young, Guido Ligthart. A comparison of different focus functions for use in autofocus algorithms[J]., 1985(6): 81-91

[2] 王子维, 戎蒙恬, 刘文江, 等. 一种基于高通滤波评价函数的自动对焦方法[J]. 信息技术, 2009 (10): 17-23.

WANG Ziwei, RONG Mengtian, LIU Wenjiang, et al. An autofocus algorithm based on high-pass filtering evaluation function[J]., 2009 (10): 17-23.

[3] 周贤. 自动聚焦的算法研究与验证平台设计[D]. 济南: 山东大学, 2006.

Zhouxian. Study on the Algorithm of Automatic Focusing and Verification platform design[D]. Jinan: Shang Dong University, 2006.

[4] 高赞, 姜威, 朱孔凤, 等. 一种自适应的自动聚焦算法[J]. 光学学报, 2006, 26(10): 1474-1478.

GAO Zan, JIANG Wei, ZHU Kongfeng, et al. An auto-adaptive algorithm to auto-focusing[J]., 2006, 26(10):1474-1478.

[5] 蒋婷, 谭跃刚, 刘泉. 基于SOBEL算子的图像清晰度评价函数研究[J]. 计算机与数字工程, 2008, 36(8): 129-131.

JIANG Ting, TAN Yuegang, LIU Quan. Research of a clarity-evaluation function of image based on Sobel[J]., 2008, 36(8): 129-131.

[6] 郑媛媛, 姜威. 一种新的自动聚焦算法的研究[J]. 光学技术, 2011, 37(4): 471-474.

ZHENG Yuanyuan, JIANG Wei. Research on a new auto-focusing algorithm[J]., 2011, 37(4): 471-474.

[7] MO Chunhong, LIU Bo.An auto-focus algorithm based on maximum gradient and threshold[C]//5t, 2012: 1191-1194.

[8] 祝世平, 房建成, 周锐. 一种新的能量谱-熵图像聚焦评价函数[J]. 北京航空航天大学学报, 1999, 25(6): 721-723.

ZHU Shiping, FANG Jiancheng, ZHOU Rui. New kind of energy-spectrum entropy image focusing evaluation function[J]., 1999, 25(6): 721-723.

[9] 王倩, 宋恩民, 许向阳, 等. 基于加权邻域相关性的显微镜自动聚焦函数[J]. 光学精密工程, 2008, 16(1): 166-171.

WANG Qian, SONG Enmin, XU Xiangyang. Auto-focusing function for microscope image based on weighted neighborhood correlation[J]., 2008, 16(1): 166-171.

The Influence of Energy Fluctuation of Image on Auto Focus Sharpness Evaluation Function

PAN Xuejuan1,2，ZHU Youpan1,2，PAN Chao1，XIA Likun3，ZENG Bangze1，LUO Lin1，ZHAO Deli1，LI Zemin1

(1.,650223,; 2.,710065,; 3.,650223,)

During the research on auto focus image sharpness evaluation function, some functions failed to evaluate image sharpness tend to have similar shape of curves, and showed a consistent trend with the average of image. The reasons are analyzed from the mathematical perspective. The effect of image energy fluctuation on evaluation function and corresponding processing method are discussed. The reference to the design and application of sharpness evaluation function for a specific auto focus system is offered.

auto focus，sharpness evaluation function，background influence

TP391.41

A

1001-8891(2016)12-1032-06

2016-09-28；

2016-12-05.

潘雪娟（1990-）女，硕士研究生，研究方向为图像处理，E-mail：1531796807@qq.com。

朱尤攀（1978-）男，研究员级高级工程师，博士研究生，研究方向为光电成像系统，E-mail：zhuypbit@aliyun.com。