考虑角点不连续因子的精细功率重构及验证

兰 兵，潘昕怿，石兴伟，陈海英，攸国顺，张春明

(环境保护部 核与辐射安全中心，北京100082)

考虑角点不连续因子的精细功率重构及验证

兰 兵，潘昕怿，石兴伟，陈海英，攸国顺，张春明

(环境保护部 核与辐射安全中心，北京100082)

在采用调制法进行组件精细功率重构时，由于改进的格林函数节块法程序引入了组件不连续因子，导致重构时角点中子通量不连续，需引入角点不连续因子进行修正保证其连续性。文中利用改进格林函数节块法程序堆芯扩散计算的结果，采用高阶多项式展开的调制法来进行组件内的精细功率重构，探讨了角点不连续因子在精细功率重构中的重要作用。并通过秦山二期实际堆芯的两种工况对其进行了验证，与SIMULATE-3的计算结果对比表明：考虑角点不连续因子的精细功率重构具有较高的计算精度，能够满足工程计算的要求。

节块法；角点不连续因子；精细功率重构

调制法精细功率重构计算快速且精度高[1]，成熟的商业核设计程序SIMULATE-3便采用这种方法进行精细功率重构[2]，但SIMULATE-3在计算角点中子通量时并非将角点中子通量展开为双二次多项式进行求解，而是简化为对中子通量进行变量分离并横向积分。由于SIMULATE-3程序中引入了组件不连续因子，四个节块内的均匀化中子通量在中心角点处不连续，SIMULATE-3引入角点不连续因子来保证重构后角点中子通量的连续性。本文则采用双二次多项式展开求解角点中子通量，并利用角点不连续因子修正角点中子通量以保证其连续性，在带组件不连续因子的改进格林函数节块法程序中[3]建立带角点不连续因子修正的21项展开式调制法精细功率重构模块，探讨了角点不连续因子在精细功率重构中的重要作用，并利用秦山二期实际堆芯的两种工况对其进行了验证。

1 基本理论

关于21项展开式调制法精细功率重构的基本理论详见参考文献[1]，本节仅介绍角点不连续因子的基本理论知识。在等效均匀化理论中，组件不连续因子是组件计算程序产生的一个非常重要的等效均匀化常数，它能够保证均匀化节块反应率、界面上净中子流和反应堆特征值的守恒，极大程度降低节块法的计算偏差。精细功率重构中角点不连续因子与节块法中组件不连续因子的基本理论思想一样，并且均是通过组件计算程序产生。其具体定义如下：

(1)

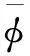
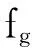
(2)

2 秦山二期实际堆芯验证

2.1 计算对象

本文采用秦山二期实际堆芯作为考虑角点不连续因子的精细功率重构验证对象，对比参考程序为SIMULATE-3。改进格林函数节块法程序对秦山二期堆芯的验证结果见参考文献[3]。精细功率重构的验证共选取了两种工况：工况一为热态零功率，控制棒都提到堆外；工况二为热态零功率，C组控制棒全部插入堆芯。为了保证计算结果与参考程序SIMULATE-3具有可比性，待验证的程序所采用的组件截面群常数和不连续因子均与SIMULATE-3保持一致。共选取了堆芯中具有代表性的3种典型节块来进行功率重构的验证，其在堆芯中的布置如图1所示。

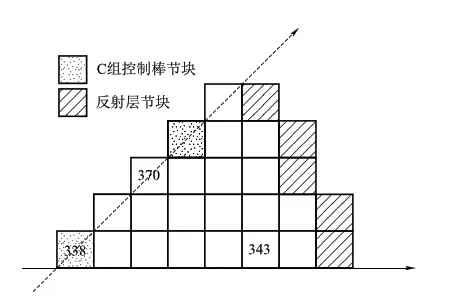
图1 精细功率重构节块在堆芯中的位置Fig.1 Position of pin power reconstruction nodal in the reactor core

2.2 工况一计算结果及分析

工况一精细功率重构功率峰值大小及位置计算结果见表1，由表可知：NNGFM AXS ADF的计算结果与SIMULATE-3相比较，3种典型节块重构功率峰值的偏差均在1%以内，但343和370节块功率峰值位置却不相吻合。NNGFM AXS ADF-CDF的计算结果与SIMULATE-3相比较，3种典型节块重构功率峰值的偏差在2%以内，并且3种典型节块功率峰值位置与SIMULATE-3高度吻合。由此可见，角点不连续因子的引入能够提高精细功率重构功率峰值位置的预测准确度。

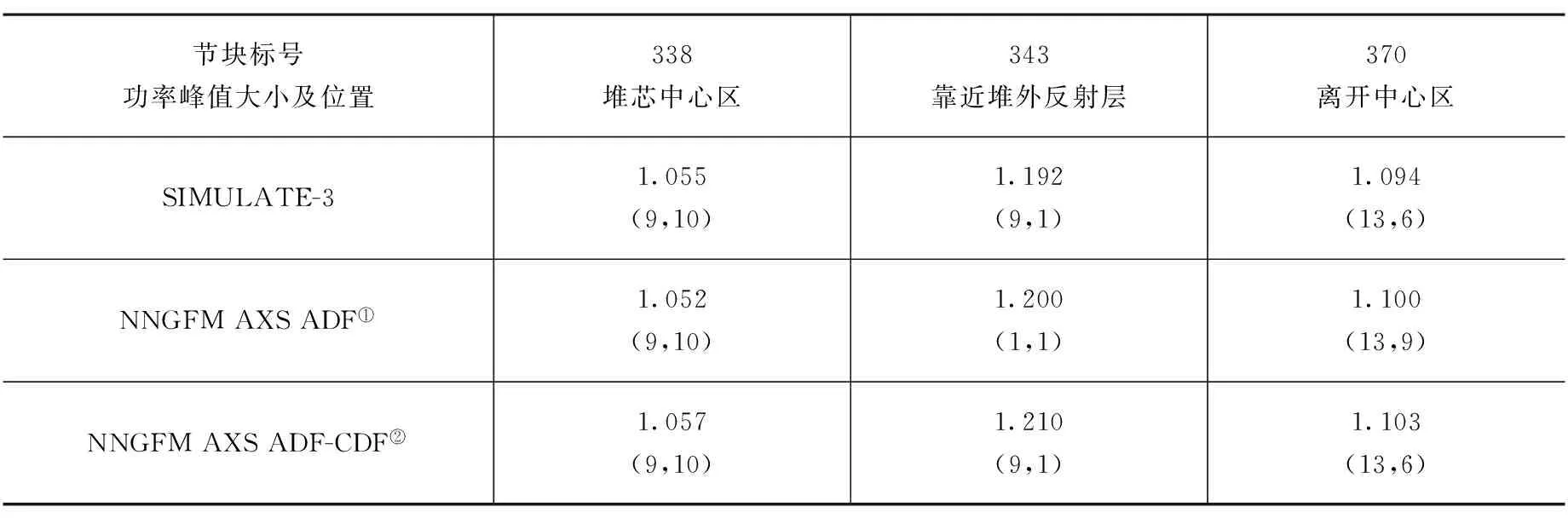
表1 工况一各典型节块精细功率重构计算结果

注：① 精细功率重构时未采用角点不连续因子进行修正(下同)

② 精细功率重构时采用角点不连续因子进行修正(下同)

为了进一步考察角点不连续因子对节块内精细功率分布的影响，分别对NNGFM AXS ADF及NNGFM AXS ADF-CDF计算的3种典型节块的内部精细功率分布与参考程序SIMULATE-3进行了比较，如图2和图3所示。虽然NNGFM AXS ADF及NNGFM AXS ADF-CDF计算得到的3种典型节块的功率峰值大小与参考程序SIMULATE-3的偏差都在2%以内，但从图2和图3可以更加形象直观看出，NNGFM AXS ADF计算的节块内部精细功率分布出现了不同程度的偏差，其中370节块角点处的功率偏差最大值超过了6%，如果采用了角点不连续因子对角点中子通量进行修正，同为370节块，NNGFM AXS ADF-CDF计算的节块内部精细功率偏差不超过2%。同样对于338和343节块，NNGFM AXS ADF-CDF重构的组件内部精细功率分布整体偏差更小。因此在精细功率重构中采用角点不连续因子不仅能够提高节块功率峰值位置的预测精确度，同时也能提高节块内部精细功率分布的整体计算精度。另外工况一并未考虑控制棒插入的效应，实际上伴随控制棒的插入，堆芯的通量梯度变得更大，相邻节块交界点处的角点中子通量不连续性更明显，角点不连续因子对节块精细功率重构的改善将更加显著，下面将对控制棒插入工况下的精细功率重构进行验证。

图2 工况一未采用角点不连续因子修正的节块内精细功率分布偏差(%)Fig.2 Relative pin power error (%) of nodal without CDF in first condition

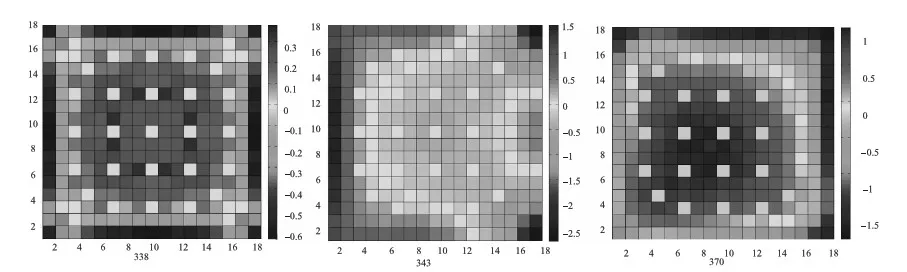
图3 工况一采用角点不连续因子修正的节块内精细功率分布偏差(%)Fig.3 Relative pin power error (%) of nodal with CDF in first condition

2.3 工况二计算结果及分析

工况二精细功率重构功率峰值大小及位置计算结果见表2，由表可知：虽然NNGFM AXS ADF计算的3种典型节块功率峰值位置与SIMULATE-3相吻合，但是C组控制棒插入的338节块功率峰值偏差达到了32.69%。而NNGFM AXS ADF-CDF计算的3种典型节块功率峰值位置不仅与SIMULATE-3相吻合，并且功率峰值的偏差均保持在2%以内。分析可知：NNGFM AXS ADF计算的338节块功率峰值偏差较大，主要是由于338节块内控制棒插入导致节块间通量梯度变大，相邻节块交界点处角点中子通量的不连续性更加明显，如果不采用上述公式(2)对角点中子通量进行修正，而强制相邻节块交界点处角点中子通量满足连续性条件，则会给计算结果带来较大偏差。

表2 工况二各典型节块精细功率重构计算结果

与工况一一样，分别对NNGFM AXS ADF及NNGFM AXS ADF-CDF计算的3种典型节块的内部精细功率分布与参考程序SIMULATE-3进行了比较，如图4和图5所示。从图4和图5可知：虽然NNGFM AXS ADF计算的370节块功率峰值与参考程序SIMULATE-3的偏差在1%以内，但其节块内部精细功率偏差最大值超过了10%，最大偏差点刚好落在靠近控制棒插入节块的交界角点处，而NNGFM AXS ADF-CDF计算的370节块内部的精细功率偏差始终保持在3%以内，这是因为在利用调制法进行精细功率重构计算时，角点中子通量的求解需要相邻节块交界点处角点中子通量连续性来构建求解的约束条件，C组控制棒插入节块刚好为370节块的相邻节块，而交界点处由于控制棒的插入角点中子通量的不连续变大，强制相邻节块交界点处角点中子通量满足连续性条件，不仅影响370节块精细功率重构的计算精度，同样影响其周围相邻的节块。而对于343节块其周围并不存在通量梯度较大的相邻节块，NNGFM AXS ADF与NNGFM AXS ADF-CDF计算的节块内部精细功率偏差均保持在4%以内。

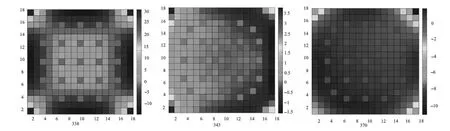
图4 工况二未采用角点不连续因子修正的节块内精细功率分布偏差(%)Fig.4 Relative pin power error(%) of nodal without CDF in second condition

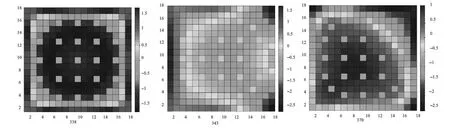
图5 工况二采用角点不连续因子修正的节块内精细功率分布偏差(%)Fig.5 Relative pin power error (%) of nodal with CDF in second condition

3 结论

本文建立了基于21项展开式调制法并考虑角点不连续因子的组件精细功率重构程序，利用秦山二期实际堆芯两种工况对程序进行了验证，与参考程序SIMULATE-3相比较，采用角点不连续因子修正角点中子通量的精细功率重构，能准确预测组件精细功率峰值及位置，如果不采用角点不连续因子进行修正，在控制棒插入工况下，精细功率重构的偏差将变得不可接受。结论如下：具有组件不连续因子的改进格林函数节块法程序采用调制法开展精细功率重构时，考虑角点不连续因子可以极大提高精

细功率重构的计算精度，使其满足工程计算的需求。

[1] 竹生东, 谢仲生. 燃料组件内精细功率的重构[J]. 西安交通大学学报, 2000, 34(5): 32-36.

[2] K. R.Rempe, SIMULATE-3 Pin Power Reconstruc-tion: Methodology and Benchmarking[J]. Nuclear Science and Engineering., 1989, 103(4): 334-342.

[3] 兰兵, 曹欣荣. 格林函数节块法程序的改进[R]. 中国核科学技术进展报告(第二卷), 2011.

[4] Han Gyu Joo, Seung Gyou Baek. Multigroup Pin Power Reconstruction with Two-dimensional Source Expansion and Corner Flux Discontinuity[J]. Annals of Nuclear Energy, 2009, 36(1): 85-97.

Corner Discontinuity Factor Applied in Pin Power Reconstruction and Verification

LAN Bing，PAN Xin-yi，SHI Xing-wei，CHEN Hai-ying，YOU Guo-shun，ZHANG Chun-ming

(Nuclear and Radiation Safety Center, Beijing 100082, China)

When the discontinuity factor introduced in the improved Green’s function code, the corner neutron flux is discontinuity, which need to be modified to ensure continuity in the pin power reconstruction. In this paper, the pin power reconstruction of improved Green’s function nodal method code is developed using the modulation method with high-order polynomial expansion, and the corner discontinuity factor’s importance is discussed. The control rod insertion and withdrawal conditions of Qinshan nuclear power plant are verified, the numerical results are compared with SIMULATE-3 code. The results show that the pin power reconstruction with corner discontinuity factor has high accuracy and can meet the requirement of engineering calculations.

Nodal method; Corner discontinuity factor; Pin power reconstruction

2016-06-14

国家科技重大专项项目资助(2013ZX06002001)

兰 兵(1986—)，男，四川省蓬安县人，硕士研究生，现从事核能科学与工程方面研究

潘昕怿：panxinyi@chinansc.cn

TL329

A

0258-0918(2016)06-0881-05