考虑土与板间摩擦力的两拼式U形复合衬砌渠道冻胀破坏力学模型

王江伟，王红雨

(宁夏大学土木与水利工程学院，银川 750021)

0 引 言

两拼式U形混凝土衬砌渠道是由两块半U形弧板在底部用水泥黏结接缝拼接而成的U形渠道，这种结构形式的渠道由于构造简单，施工方便，目前广泛应用于宁夏引黄灌区。由于本地区存在着严重的季节性土体冻融现象，常导致渠道衬砌体因土体冻胀而发生破坏，从而降低甚至达不到防渗节水的效果。渠道防冻胀定量化研究的关键是准确分析渠道衬砌体在冻胀时的受力情况，建立渠道冻胀破坏的力学模型。李翠玲[1]通过建立两拼式U形渠道力学模型，分析了两拼式U形渠道的受力情况及破坏特征，推导出渠道冻胀控制内力及最大拉应力的计算公式，并给出了衬砌结构胀裂部位、衬砌板厚及抗冻胀破坏验算的方法，结果表明，两拼式U形渠道衬砌结构法向冻胀力小、分布均匀、恢复力大、整体适应变形及抗冻胀能力强。然而，该力学模型中并没有考虑复合衬砌结构中土工膜与渠基土之间的相互作用，土工膜是一种柔性材料，木身具有很好的伸缩性能，加之土工膜有很好的防渗作用[2,3]，能减少冻胀的水源补给，可以减小一部分冻胀变形，又由于渠基土对复合衬砌体的摩擦力减小[4]，导致渠基土对衬砌体的滑动约束减小，在冻胀作用下衬砌体将会在复合土工膜和渠基土接触面上产生一定的冻胀位移量，使得渠基土对衬砌体的切向变形约束减小，从而起到抗冻胀的作用。本文结合宁夏引黄灌区渠道衬砌实际情况，采用土工膜混凝土复合衬砌，将摩擦力考虑在内建立了力学模型，分析了刚柔材料复合衬砌下渠道衬砌结构受冻融作用时的内力情况，并通过算例将土工膜混凝土复合衬砌结构与传统的混凝土衬砌结构进行了对比验证，研究结果对西北地区U形混凝土防渗渠道的抗冻胀决策有一定参考价值。

1 力学模型建立

寒冷冻土区的土体，在温度梯度和水分迁移的影响下会发生冻结和冻胀，体积会随之增大并产生冻胀量,若无外界约束，冻胀量将能自由释放，但是在混凝土衬砌渠道中，土体的自由冻胀被衬砌体约束，衬砌体会对土体产生一定的约束力，反之土体将会对衬砌体产生相应的约束反力，垂直于衬砌体的约束反力称为法向冻胀力，平行于衬砌体的约束反力称为切向冻结力，衬砌体最终在冻胀力、冻结力共同作用下发生破坏。采用土工膜混凝土复合衬砌的衬砌体在土工膜与渠基土之间摩擦力减小的情况下会产生一定程度的冻胀位移量，使得作用在衬砌体上的有效冻胀力、冻结力减小，与重力、弧板与弧板之间的相互约束力等重新分布达到平衡。

1.1 摩擦力分析

在已经建立的渠道抗冻力学模型中，忽略土与衬砌板、土工膜之间的摩擦力不尽合理，渠基土与各种衬砌结构之间由于内摩擦角的存在，它们之间的摩擦力是真实存在的，且在受力分析中占据重要比重，所以在建立力学模型时必须考虑土与衬砌结构之间的摩擦力。土工膜的上层一般采用的是现浇混凝土，可以将混凝土与土工膜看成一个整体，因此，对于用混凝土与土工膜复合衬砌的渠道来说，摩擦力应该考虑的是土工膜与土体之间的摩擦力，而不是土工膜与混凝土之间的摩擦力。又由于复合土工膜与土体之间的摩擦角一般小于土体本身的内摩擦角[4-7]，也就是土工膜与下层土体之间的摩擦系数小于土体本身内部之间的摩擦系数，从而导致复合衬砌体与渠基土体之间摩擦力的减小，所以在土体发生冻胀情况下，复合衬砌体就会产生允许范围内的冻胀位移量，使得渠基土对衬砌体的切向约束减小。

1.2 模型基本假设

两拼式U形复合衬砌渠道由于渠底埋深较浅，渠顶较深，渠底的冻胀量较大，冻胀变形分布不均匀，使得衬砌结构在冻胀力、冻结力、底板与底板相互约束力、土工膜与渠基土之间的摩擦力共同作用下成为偏心压弯构件，另外，由于混凝土衬砌板的刚度相对较小，抗拉和抗弯能力较差，随着冻胀的逐渐加剧，当衬砌弧板承受的弯矩和拉应力超过混凝土衬砌板的极限承载力和变形量时，衬砌结构就破坏了，所以在建立力学模型时，需要根据以上冻胀破坏的特征和原因提出以下相应假设[8,9]。

(1)土工膜混凝土复合衬砌板和渠基冻土均为弹性材料，渠基土的弹性模量远小于混凝土衬砌板的弹性模量。

(2)渠基土在冻结前已经固结完毕，不考虑未冻结土的压缩效应。

(3)就整个渠道而言，近似为单向冻结，不考虑纵向变形的影响。

(4)整个弧板的冻胀量沿弧板呈线性分布，弧底最大，弧顶最小，法向冻胀力受冻胀量的影响，弧板上的法向冻胀力沿弧长也呈线性分布，弧顶为零，弧底达到最大值；切向冻结力在弧顶和弧底均为零，弧板上的切向冻结力沿弧长呈线性分布，其最大值在弧板中部左右。

(5)由于坡顶受法向冻结力约束，坡脚受底板相互约束，所以衬砌板可以简化为两端固定的简支梁，弧板法向冻结力可以简化为弧板顶部的集中荷载，从理论上讲，弧板上部法向冻结力的合力点不应在弧板最顶端，而应偏下一些，简化时取在最顶端，这样使计算更偏于安全。

(6)弧底板采用水泥接缝的目的是为了削弱冻胀变形、减轻冻胀破坏，故可将弧板与弧板接缝处简化为固定铰支座。

(7)将土工膜与混凝土板看成一个整体，在渠基土冻胀和底板顶推作用下产生摩擦力，摩擦力在弧板呈线性分布，在弧底中心线上为零，在弧板顶部最大。

(8)两拼式U形复合衬砌渠道可简化为由渠顶法向冻结力提供约束，在法向冻胀力、重力、切向冻结力、土工膜与渠基土摩擦力共同作用下，保持静力平衡的薄壳拱形结构。

1.3 渠道断面图与受力图

两拼式U形渠道复合衬砌结构断面图如图1所示。设弧板的半径为R，圆弧中心角为2α，弧长为L，衬砌板厚为b。

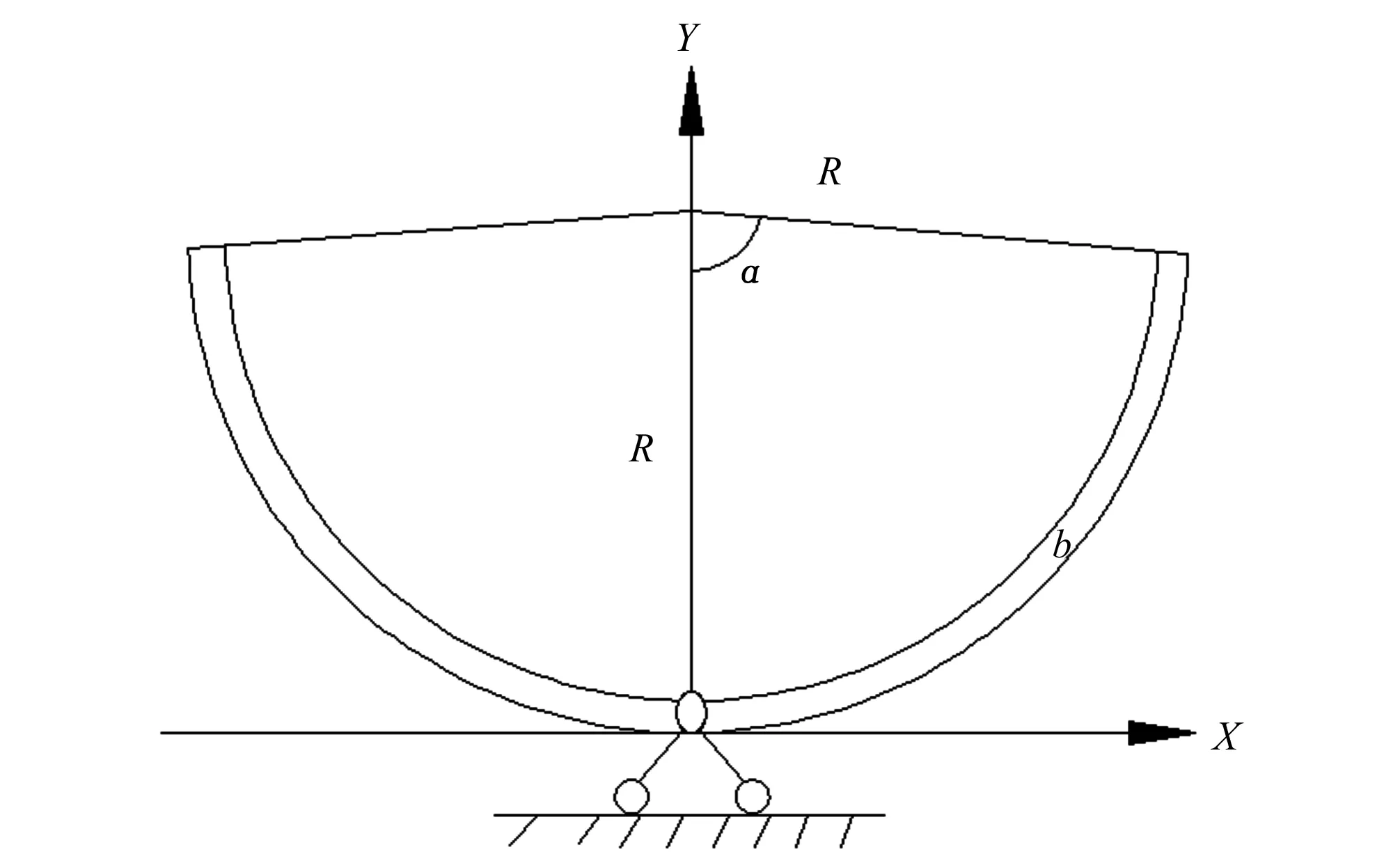
图1 两拼式复合衬砌U形渠道断面图Fig.1 Section of composite lining u-shaped canal with splicing two arc-plates

两拼式U形断面渠道复合衬砌结构阴坡上的法向冻胀力为q、冻结力为F、切向冻结力为τ，摩擦力为τ1，对阳坡的有关外力约定在其相关变量符号右上角加一撇，且阴坡的外力大于阳坡对应的外力，极限平衡状态时，受力分布如图2、图3和图4所示。

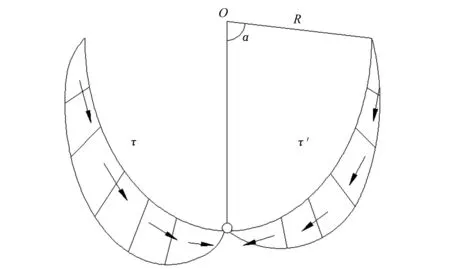
图3 切向冻结力分布Fig.3 Distribution of tangential freezing force

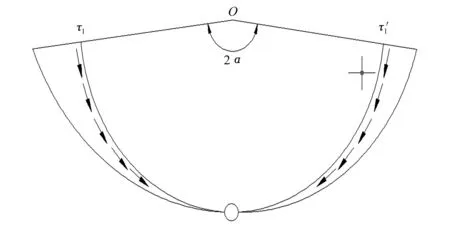
图4 复合衬砌摩擦力分布Fig.4 Distribution of fraction of composite lining

1.4 建立静力平衡方程

根据假设，在冻胀破坏作用下渠道衬砌板达到极限平衡状态时，切向冻结力的最大值 为渠道阴坡衬砌板与渠基土之间的最大冻结力，其大小由土质、负温及渠基土含水量等条件决定，属于已知力,渠道阴坡与阳坡的计算简图相似，只是其上作用荷载数值不同，衬砌板与土体之间的摩擦力与法向冻胀力线性相关。根据分析和假设，考虑到渠道的走向、阴阳坡最低温度等因素，并结合实际情况，阴阳坡的冻胀量、变形量近似成一定的比例，所以假设阴阳坡的外作用力如冻胀力、冻结力、摩擦力成一定的比例，所以可得:

(1)

式中：q0为阴阳坡最大法向冻胀力；τ0为阴坡最大法向冻结力；τ1为阴坡衬砌板与土之间的摩擦力；F为阴坡弧板顶部法向冻结力；m为比例常数，与渠道走向、阴阳坡最低温度有关(对阳坡上的有关外力在相应符号右上角加一撇以示区别)。

由∑X=0得：

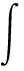
(2)

由∑Y=0得：

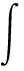
(3)

其中

τ1=μq

(4)

联解以上3个方程，即可得到q0、F的解，进一步便可计算结构其他内力。

2 力学模型的求解

2.1 弧板的计算简图

根据以上分析，沿弧板线性分布的法向冻胀力最大值为q0位于弧底，沿切向呈线性分布的最大冻结力为τ0位于弧板中部左右，沿弧长分布的重力为ρgb,沿弧板呈线性分布的摩擦力为τ1，法向冻结力F,弧板间相互约束弯矩、轴力、剪力分别为M0、N0、Q0,则弧板可以简化为在这几种力共同作用下的简支梁，其计算简图如图5。

广州“好教育”的提出和推进，得益于一位有情怀的人，他就是今日广州教育的掌舵人与总设计师—市教育局局长屈哨兵。在广州教育发展的征途上，屈哨兵如同他的名字一样刚正、坚毅、有责任心，是一位恪尽职守的“哨兵”，他充分展现出了儒雅大方、幽默风趣的人格魅力，对教育功能、教育发展的深刻思考和独到见解，以及几十年投身教育事业、初心不改的教育情怀。

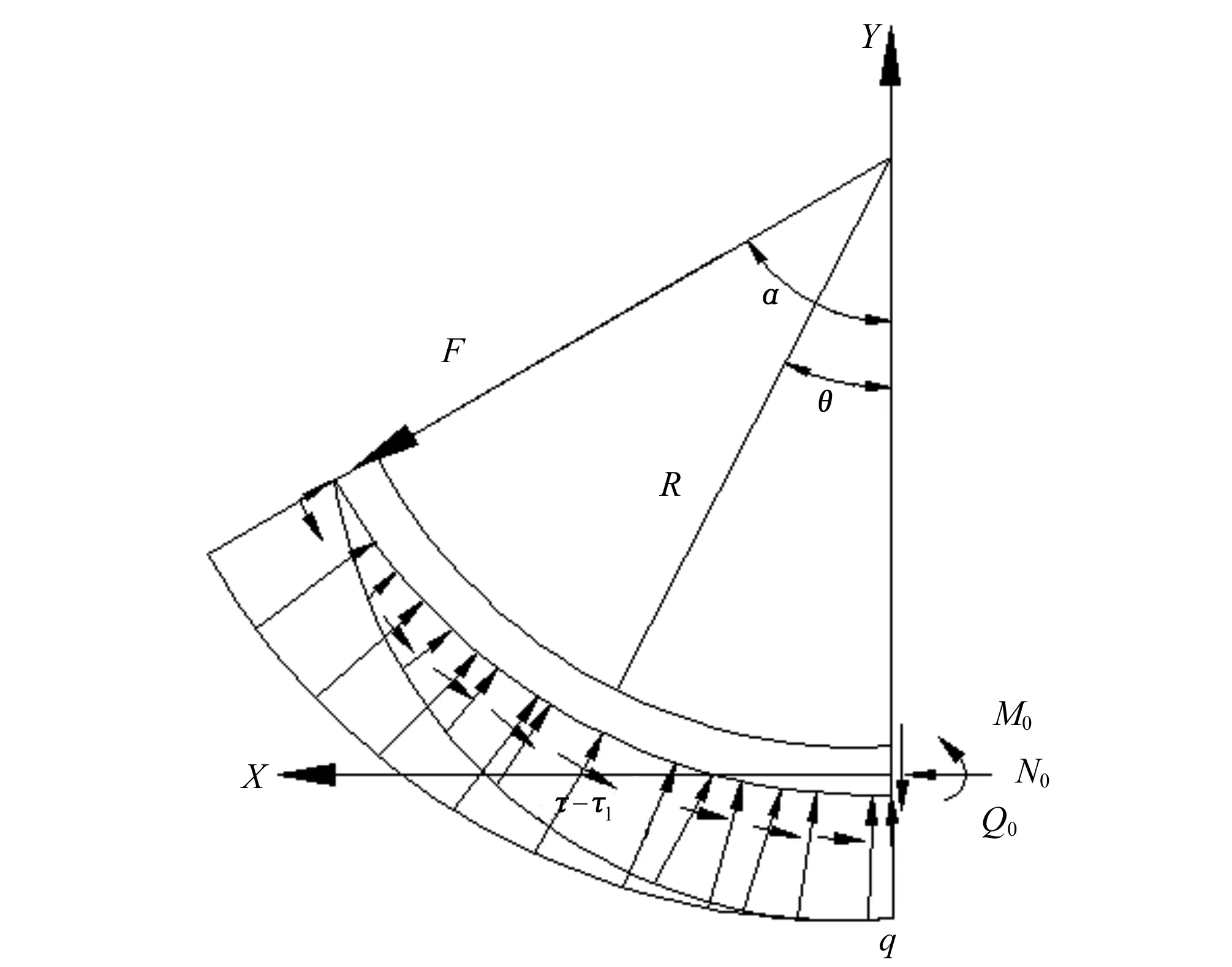
图5 弧板计算简图Fig.5 Calculating diagram of arc-plate

2.2 弧板内力求解

以弧底中心处(见图5)为坐标原点，根据静力平衡条件可得与中心线成θ角处的轴力、剪力、弯矩为：

(7)

最大弯矩界面:

(8)

最大弯矩：Mmax=Mθ0

最大轴力：Nmax=Nθ0

由以上各式可以画出衬砌板内力分布图如图6,由内力分布图可以看出，弯矩最大值发生在板中间部位，即该处最容易发生破坏，这与实际渠道工程破坏部位相一致。

图6 弧板内力简图Fig.6 Internal forces diagram of arc-plates lining

2.3 力学模型的讨论

(1)本模型是根据渠道冻胀破坏的规律，结合各种已建渠道模型[10-13]，通过适当假设和简化，将衬砌板与渠基土之间的摩擦力考虑在内，建立的两拼式U形复合衬砌渠道的冻胀破坏力学模型。

(2)此力学模型是假设渠道衬砌体两侧受力不一样的情况下建立的，由于渠道的走向、阴阳坡的影响[14,15]使得渠道阴阳坡面的冻胀力、冻结力大小不同，所以为了计算的准确性，阴阳坡的冻胀力应按实际情况进行分析。

(3)所建立的力学模型是将渠道弧板所受的法向冻结力简化为集中力进行计算的，而实际上法向冻结力也是沿弧板呈一定分布的，其精确分布还无法确定，所以如何确定法向冻结力沿弧板的分布情况还有待进一步研究。

(4)对于两拼式U形复合衬砌渠道，法向冻胀力、摩擦力、重力及切向冻结力产生的弯矩的正负与混凝土衬砌渠道相同，所不同的是正负弯矩的大小发生了变化，复合衬砌渠道的破坏弯矩要小于混凝土衬砌的破坏弯矩。另外，最大弯矩发生在与中心线成45°附近，这正是两拼式U形渠道往往从衬砌板中部发生折断破坏[16]的原因。

2.4 两拼式U形渠道复合衬砌板厚度及抗裂验算

对于由两块半U形弧板拼接的渠道，其弧板受力形式可近似简化为压弯构件，复合衬砌板是否发生冻胀破坏，将由衬砌板最大弯矩处的最大拉应变是否超过其允许拉应变决定，一般情况下剪力不参与渠道衬砌板的冻胀破坏。

渠道衬砌板最大拉应力在最大弯矩所在的部位，其最大拉应力计算如下:

(9)

式中：弯矩和轴力的表达式同前。

对应的最大拉应变及抗裂条件为:

(10)

式中：Ec、εt可据相关规范手册查得。

3 应用实例

某两拼式U形渠道，由C20混凝土构成，材料密度ρ=2 500 kg/m3，板弧长L=3 m，弧板半径R=2 m，衬砌板厚b=0.15 m，圆弧中心角2α=120°，渠基土为粉质土，土工膜与渠基土摩擦角为5°，冻土层最低温度为-15°，判断该衬砌结构是否发生冻胀破坏。( 混凝土的极限拉应变εt=1.0×10-4，弹性模量Ec=260 GPa)。

3.1 土工膜混凝土复合衬砌形式结构计算

(1)最大切向冻结力计算。由经验公式得：

τ0=c+mt=9.4 kPa

式中：c,m为与土质有关的系数(c=0.3～0.6 kPa,m=0.4～1.5 kPa/℃，有地下水补给的、渠基土含水率越大、土壤黏粒含量占的百分比越大，冻结速率越快的，其c,m取值就越大，本例中c取0.4，m取0.6)。

(2)复合衬砌渠道最大法向冻胀力、摩擦力计算。

由式(2)～(4)可得：q0=5.15 kPa,τ1=0.36 kPa 。

(3)复合衬砌渠道弧板内力计算及冻胀破坏判断。按式(8)计算得θ0=40°，按式(5)计算得Nθ0=15.15 kN，按式(7)计算得Mθ0=8.04 kN·m，按式(9)计算得σmax=2.39 MPa，而混凝土板的极限拉应力σt=εtEc=2.6 MPa, 由σmax<σt,所以衬砌板不会发生冻胀破坏。

3.2 混凝土衬砌形式结构计算

(1)渠道最大法向冻胀力由式(2)～(4)得：q0=5.44 kPa 。

(2)弧板内力计算与冻胀破坏判断。按式(8)计算得θ0=40°，按式(5)计算得Nθ0=18.15 kN，按式(7)计算得Mθ0=9.11 kN·m，按式(9)计算得σmax=2.55 MPa，由σmax<σt,所以衬砌板不会发生冻胀破坏。

3.3 计算结果比较

通过对复合衬砌结构和混凝土衬砌结构相比可以看出，复合衬砌结构法向冻胀力、拉应力均比混凝土衬砌结构小，表明由于土工膜与渠基土之间的摩擦力的减小，衬砌板与土体之间产生了一定量的相对位移，土体对衬砌体的法向和切向约束减小，有效冻胀力、冻结力均得到减小，抗冻胀能力有所增强。

4 结 语

(1)对比两拼式刚性混凝土衬砌渠道，加入复合土工膜后，削减了冻土对衬砌板的切向约束力，改善了衬砌体本身的受力状态，使得冻胀量分布更加均匀，加之土工膜有很好的防渗作用，能减小冻胀的水源补给，所以，土工膜与混凝土板相结合的复合衬砌形式有利于渠道的抗冻胀破坏，当然，有关土工膜的破坏、补修形式、两块底板之间的相互约束力及底板之间的缝隙防渗还需要进一步研究。

(2)本文在计算时，假设渠道整体达到极限状态时，复合衬砌体不会发生局部破坏，但是，由于施工或者结构、断面形状、尺寸等原因，有可能渠道衬砌体局部发生破坏时渠道整体还未达到极限状态，所以本模型求解的内力是偏安全的。

(3)本文是在考虑了土工膜与渠基土之间摩擦力的基础上建立的力学模型，考虑了摩擦力之后将会导致渠道的最大受力发生变化，但是土工膜与渠基土之间的摩擦力分布及摩擦系数还有待进一步研究。

(4)当土工膜与渠基土之间不设排水时，由于土工膜本身的渗漏以及雨水入渗等，会对土工膜产生反向水压力，易导致土工膜鼓起以致滑落，对稳定不利，所以还应考虑土工膜与渠基土之间的抗滑稳定性。

总之，正是由于两拼式U形复合衬砌体与渠基土之间摩擦力减小的原因，导致衬砌体切向受力减小，削弱了渠基土对衬砌板的切向约束，使衬砌体产生了允许范围内的冻胀位移量，并对衬砌体内力进行了重新分布，使其内力明显减小，改善了衬砌体的受力状况，抵抗破坏能力有所增强。

□

[1] 李翠玲,王红雨.两拼式U形渠道混凝土衬砌结构冻胀破坏力学模型[J].中国农村水利水电，2014,(5):86-89.

[2] 王绪存，王红雨.土工膜的防渗作用机理及其在扬黄渠道中的应用[J].农业科学研究，2008,29(2):29-33.

[3] 陈立杰，蔡雪雁，王正中.复合土工膜与纳米混凝土衬砌渠道冻胀模拟[J].中国农村水利水电，2010,(8):106-109.

[4] 岑威钧，沈长松.复合土工膜防渗土坝坝坡的抗滑稳定性研究[J].水利规划设计，2002,(4)：54-56.

[5] 姜海波，侍克斌.坝坡复合土工膜防渗体的抗滑稳定分析[J].水资源与水利工程学报，2010,21(6):15-18.

[6] 姜海波，侍克斌，刘 亮.复合土工膜与粗粒料的摩擦特性试验研究[J].中国农村水利水电，2011,(3):86-89.

[7] 张广禹，李振灵.西霞院反调节水库复合土工膜摩擦系数研究[J].华北水利水电学报，2007,28(1):32-35.

[8] 余书超，宋 玲.刚性衬砌渠道受冻胀时衬砌层受力的试验研究[J].中国农村水利水电，2001,(9):4-5.

[9] 张国军，陆立国.影响衬砌渠道冻胀破坏严重的关键因素[J].中国农村水利水电，2012,(9):105-108.

[10] 王正中.梯形渠道混凝土衬砌冻胀破坏的力学模型研究[J].农业工程学报，2004,(3):24-29.

[11] 王正中，李甲林，陈 涛，等.弧底梯形渠道混凝土衬砌冻胀破坏力学模型研究[J].农业工程学报，2008,24(1):18-23.

[12] 李学军，费良军，穆红文.U形衬砌渠道冻胀机理与防渗技术研究[J].干旱地区农业研究所，2006，24(3):194-199.

[13] 张 茹，宋孝斌.大U形混凝土衬砌渠道冻胀破坏的力学模型探讨[J].东北水利水电，2008,36(11):217-223.

[14] 黄秀芳，刘新生.渠道混凝土板砌护冻胀分析与实施U型断面砌护浅析[J].甘肃农业，2008,(12):77-79.

[15] 陈 涛，王正中，张爱军.大U形渠道冻胀机理试验研究[J].灌溉排水学报，2006,25(2):8-10.

[16] 朱 强.我国渠道冻胀防治综述[J].防渗技术,1996,2(2):7-16.