均匀设计下丹江口水库水质参数敏感性度量

段 扬，胡伏生，王 旭，雷晓辉

(1.中国地质大学(北京)水资源与环境学院，北京 100083； 2.中国水利水电科学研究院，北京 100038)

0 引 言

大型湖泊及水库水质模拟是研究其生态演变，污染物运移，富营养化等问题的基础，其模拟的关键是参数的不确定性、模拟的准确性以及参数之间的影响程度等等一系列问题，使水动力模型的率定带来了很大的难题，那么如何简单、快速地对模型各参数的敏感性进行评价也就成为重中之重。伴随着诸如光合作用、基础代谢作用、水解作用、光解作用等一系列生化反应的进行，其模拟所需的参数众多，前人在这些方面做了大量的工作[1]，尤其是在多参数体系下的反演算法。截至目前，参数之间敏感性度量的主要方法为多次单因素试验法以及正交试验法。前者方法简单，操作性强，但其具有较强局限性，尤其是在试验因素及因素水平较多的情况下常常会得出错误的结论，使结果失真；后者是在全面试验基础上挑选一些代表性点进行试验，使其可以合理反映试验范围内各因素与指标间的对应关系，但其局限性在于当因素水平较高时试验次数显著增加，可操作性降低。而我国科学家方开泰及王元于1978年所提出[2,3]的均匀设计法，可以较好地实现在多因素、多水平的试验中通过较少试验次数达到最有效的选择试验点并得到关于系统尽可能充分信息的目标。

基于此，通过大量文献考究和参数权重分析，拟采用均匀设计方法进行试验设计，以丹江口水库作为研究对象，利用全回归分析手段对参数进行敏感性分析，确定了各参数对模型不确定性的影响大小，并为模型率定提供了基础，将有利于后期水质模拟分析。

1 研究方法

本文选取了美国William and Mary大学的John Hamrick所开发的综合性水质模型EFDC建立丹江口水库的三维水动力学及水质模型，其可以在河流、水库、海洋等多种水体进行一二三维的水动力学水质模拟，在国内外获得了广泛应用[1,4-9]。其在水动力学方程中满足Boussinesq近似、静水压近似以及准3D近似等基本假设条件；在水质模块中，选用质量守恒方程作为其控制方程模拟水力输运作用、吸附解析作用、藻类吸收及化学反应作等影响水体水质变化过程。公式(1)为水质模块控制方程：

(1)

式中：C代表水质状态变量浓度；u，v，w代表x，y，z方向速度分量；Kx，Ky，Kz代表x，y，z方向的湍流扩散系数；Sc代表每单位体积内部与外部的源和汇。

2 模型率定

进行参数敏感性分析的前提需建立起准确的水动力学及水质模型。本文经过不断试算最终确定选用500 m×500 m矩形网格，分为142行，79列，共计2155个。垂向上分为5层。综合考虑丹江口水库的入出流情况，选取较大的河流作为出入库边界，将附近的小河并入其相邻的主河道中，最终包含有3个入流边界、1个出流边界及1个水位边界。同时设置7个监测点来进行实测与模拟数据对比。

模拟所需气象数据选取水库周围3个气象站点加权平均值。模拟时间从2012年3月27日-2012年12月31日，时间步长为20 s，初始流速场为0，初始水位场为145 m，水质初始场由分布在库区内的7个监测站点数据经插值得到。

模型率定考虑了丹江口水库的水位、水温及水质的实测结果，模拟了其在水动力模型基础上的动态结果(图1、图2及图3)，发现模拟结果与实测值拟合度较好，其中水位误差在0.1%左右，7个监测站点水温平均误差为5.65%，氨氮平均误差为16.44%，可以较准确地反映丹江口水库的水位、温度及水质在一年中的动态变化趋势，可以作为后续参数敏感性分析的基础模型。

图1 丹江口大坝2012年模拟实测日水位过程图Fig.1 Water level process map of simulated and Measuredvaluesin front of the Danjiangkou Dam

图2 凉水河站水温模拟实测值对比图Fig.2 Comparison between simulated and measured water temperature values in Liangshuihe Point

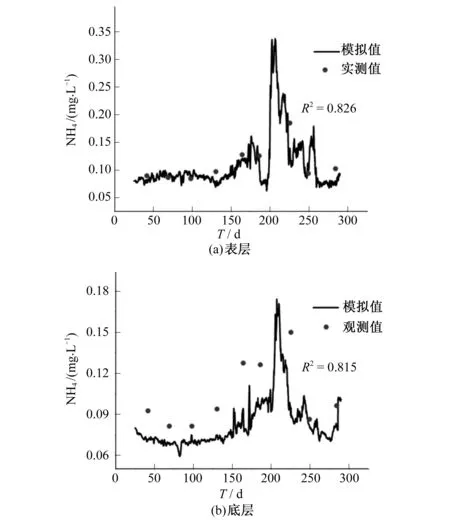
图3 凉水河站氨氮模拟实测值对比图Fig.3 Comparison between simulated and measured ammonia nitrogen values in Liangshuihe Point

3 参数敏感性分析

3.1 理论基础

选取氨氮作为参数敏感性分析的目标，其主要源项包括：①藻类基础代谢、捕食；②溶解性有机氮的矿化作用；③沉积床和水柱界面的交换。主要汇项包括：①藻类吸收；②硝化作用。氨氮含量的计算方程见下式(2)：

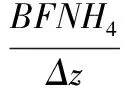
(2)

式中：NH4为水中氨氮的含量；FNIx为藻类群x(包含蓝藻、绿藻、硅藻，本次模拟仅考虑蓝藻，后同)代谢的氮中所生成的无机氮部分；BMx为藻类基础新陈代谢速率；FNIP表示被捕食的氮中所生成的溶解性有机氮部分；PRx为藻类捕食速率；PNx为藻类铵吸收偏好；Px为藻类生产速率；ANCx表示藻类氮对碳比例；Bx为藻类藻类生物量；KDON表示溶解性有机氮矿化速率；Nit为硝化速率；BFNH4为沉积物-水的铵交换通量；WNH4表示铵的外部负荷。

3.2 评价参数体系

通过文献调研[10-14]，选择藻类基础新陈代谢速率(BMR)、藻类捕食速率(PRR)、藻类生长吸收氮半饱和常数(KHN)、藻类生长速率(PM)、溶解态有机氮水解速率(KDN)、硝化作用半饱和常数(KHNITDO)、最大硝化速率(NITM)等7个参数作为敏感性分析的输入参数。假定参数间相互独立，根据已有文献[11-15]确定参数最大值与最小值范围(见表1)。

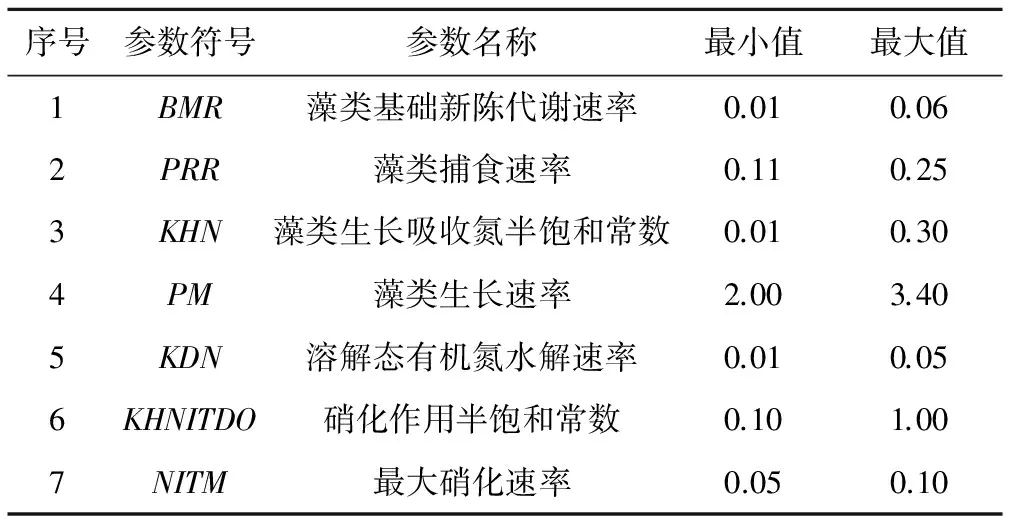
表1 参数敏感性分析模型输入参数的范围Tab.1 Ranges of parameters used for the parameter sensitivity analysis model

本次采用的均匀设计试验方法，其优点在于每个均匀设计表都会有一个使用表，可指导我们如何选择均匀设计表中的某些列来进行试验设计以及由这些列所组成试验方案的均匀度，而均匀度的好坏一般用均匀度的偏差D来衡量，其值越小，表明均匀度越好。

3.3 参数变换

通过查阅均匀设计表[12]筛选出符合条件的所有表，对比当S=7时的均匀度偏差D，选出当D最小时的方案，最终确定为U*28(288)，D=0.155 0。考虑到所有参数取值范围中中最大值与最小值相差达340倍，直接做回归分析效果欠佳，需首先对各参数进行对数变换[13]，变换后具体试验参数列表见表2。

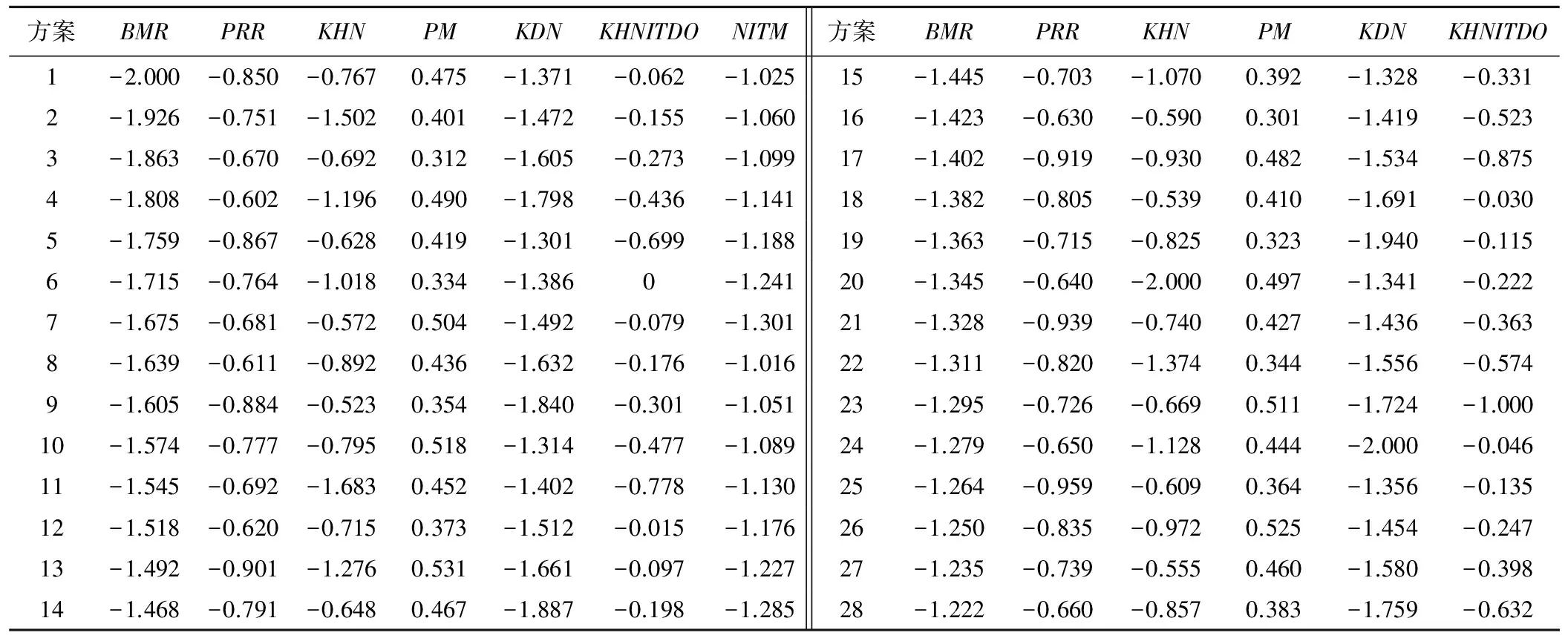
表2 均匀变换参数表Tab.2 Parameters for uniform design

将表2中参数分别带入EFDC模型中，运算28次，得到28组特定目标的结果。将7个监测点的氨氮浓度序列输出，并选取4月1日，7月15日，10月1日，12月1日4个时间点来反映氨氮浓度一年内变化情况。之后将7个监测点在4个具体时间的数值与其对应参数耦合后分别进行回归分析，研究这7个参数对于模型模拟结果的不确定性影响。

4 结果与讨论

4.1 不确定性影响

以7个监测点分别在4个具体时段的氨氮含量作为输出值，对28种参数变化环境下所得结果进行不确定性分析。以何家湾站点4月1日计算结果为例，在28次试验过程中其氨氮含量最大值为0.122 mg/L，最小值仅为0.005 8 mg/L，二者相差21倍，表明由于参数不同对于氨氮含量产生较大变化，证明参数不确定性将直接导致模型结果不确定性。通过各点氨氮浓度变化方差可以更明确地反映其不确定性大小，详见表3。

由于方差越大表征参数对于模型计算不确定性影响越大[15]，在春季各点方差值大致相同，均保持在0.03左右，仅在江北大桥处略小；而夏季由于各类生化反应进行较旺盛，由于参数不确定所造成的模型结果差异程度被放大，方差范围为0.004～0.062，且库区北部由于受到汉江及丹江入流影响其不确定性增大；秋季同夏季情况类似，但由于入流量降低且主要入流量来自于汉江使得西北部肖川站点不确定性达到最大；而冬季随着温度及日照减少，生化反应速率降低，模型趋于稳定，各点方差相差不大，仅有凉水河相较其他站点略大。

表3 各观测站点不同时段氨氮浓度方差汇总表Tab.3 Variance of ammonia nitrogen in each monitoring point

4.2 参数敏感性分析

将7个样本点的计算进行回归分析，并利用方差检验来判断试验结果的可靠性。首先，将之前设置的7项敏感性参数候选项作为自变量，将氨氮浓度作为因变量带入回归分析软件中进行自动建模，可以初步对于自变量相对重要性进行判断。以陶岔站7月15日计算结果为例，经过自动线性建模得到其准确度为90.7%，之后得出各变量相关重要性图，即各个参数对于模型不确定性的贡献率，见图4。

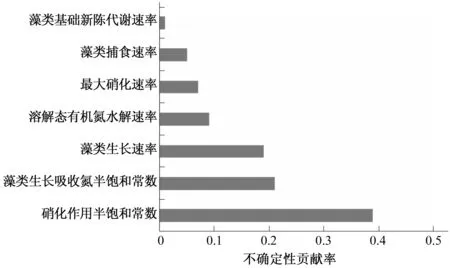
图4 7个参数对于氨氮含量不确定性贡献图Fig.4 Level of contributions to the uncertainty for the 7 parameters in ammonia nitrogen

可以看出：硝化作用半饱和常数对于氨氮含量不确定性最大，达到39%；其次是藻类生长吸收氮半饱和常数以及藻类生长速率，分别为21%和19%；前3项占到总贡献度的80%，后面四项参数贡献度较低。

由于自动建模无法求得模型方程及每项参数的回归系数，所以之后将进行全回归分析。由于篇幅限制，仍以陶岔站7月15日结果为例，取显著性水平α=0.05，样本数量为28，检验值F=23.245，通过查表查得F7,20(0.05)=2.514，可以看出F>F7,20(0.05)，表明氨氮的变化确实由于上述7个参数的变化所引起，回归方程显著。另外通过查验7个参数的相关系数发现，其中任意2个参数相关系数最大值为0.3，相关性较低，验证了之前关于7个参数相互独立的假设。

经过回归分析可以得到各个参数的标准回归系数并建立回归方程：

NH4=0.057+0.125×BMR-0.131×PRR+

0.483×KHN+0.347×PM+0.319KDN+

0.645KHNITDO-0.232×NITM

(3)

其中，藻类捕食速率(PRR)及最大硝化速率(NITM)与氨氮浓度均呈负相关关系。

将各参数回归系数及t检验绝对值进行排序可得出参数敏感性大小顺序为：硝化作用半饱和常数(KHNITDO)>藻类生长吸收氮半饱和常数(KHN)>藻类生长速率(PM)>溶解态有机氮水解速率(KDN)>最大硝化速率(NITM)>藻类捕食速率(PRR)>藻类基础新陈代谢速率(BMR)。

顺序与图5中对不确定性贡献大小顺序相同。对比同一监测点4个时段的回归系数结果可发现在一年的不同时段，参数敏感程度略有不同。以肖川站为例，表4显示的是其在各时段内各参数回归系数大小。可以看出，硝化作用半饱和常数在4个时段回归系数均位于首位且远大于后面各参数，然而之后排位与季节有较大关系，春季由于水中氨氮含量不高使得硝化作用进行程度较低，由于经过冬季有机残渣的分解及藻类死亡所释放处的溶解性有机氮的矿化水解作用得到增强；而夏季由于气温与日照较强，藻类生长茂盛，其生长过程所吸收氮成为影响氨氮浓度的一个重要因素，且同时硝化作用作为好氧反应受到夏季溶解氧含量降低影响而减弱；到了秋季，上游地区存在许多未被作物吸收的氮肥随降雨径流进入库区，且此时入流量的快速增加且其中含有大量氨氮，氨氮数量充足，使得硝化作用进行充分，此时最大硝化速率将在很大程度上影响氨氮浓度变化。其他站点结果类似，仅在少数排位上存在偏差，但并没有发生较大地区差异。

表4 肖川站各时段参数回归系数表Tab.4 Regression coefficients in different period in XiaoChuan

5 结 语

(1)根据丹江口水库的底部高程、气象、水文、环境实测数据，基于EFDC模型，建立三维水动力水质模型，并将模拟结果与实测数据进行对比取得了良好的效果，表明模型具有很强的精确度。

(2)在已率定模型基础上，以氨氮为目标，选择藻类基础新陈代谢速率等7个参数进行参数敏感度分析。利用均匀设计理论设计试验，可以在较少试验次数的情况下充分利用模型信息，快速准确地实现参数敏感度大小判断。

(3)通过对计算结果进行不确定性分析可知，参数改变对于氨氮含量影响较大，其最大最小值相差可达20余倍。

(4)经过对7个监测站点4个时段结果的比较，发现硝化作用半饱和常数敏感度最大，其次是溶解态有机氮水解速率、最大硝化速率、藻类生长吸收氮半饱和常数，而藻类生长速率、藻类基础新陈代谢速率、藻类捕食速率的敏感度较低。故今后对于其他大型水库水质模型率定时可对敏感度较低的参数采用经验参数，提高率定工作效率。

□

[1] Cerco C F, Cole T M. Three-dimensional eutrophication model of Chesapeake Bay[J]. Journal of Environment Engineering, 1993,119:1 006-1 025.

[2] 方开泰.均匀设计与均匀设计表[M].北京:科学出版社,1994.

[3] 燕 乔,吴长彬,张 岩. 基于均匀设计的邓肯E-B模型参数敏感性分析[J]. 中国农村水利水电，2010,(7):82-85.

[4] Ji Z-G. Review of hydrodynamics and water quality: modeling rivers lakes[J]. Journal of Hydrologic Engineering, 2009,(8):892-893.

[5] Jin K R, Hamrick J H, Tisdale T. Application of three-dimensional hydrodynamic model for Lake Okeechobee[J]. Journal of Hydraulic Engineering-Asce, 2000,126:758-771.

[6] 李云生,刘伟江,吴悦颖,等. 美国水质模型研究进展综述[J]. 水利水电技术,2006,(2):68-73.

[7] Jin K R, J M Harmrick, T S Tisdale. Application of a Three-dimensional hydrodynamic model for Lake Okeechobee[J]. Journal of Hydraulic Engineering, 2000,106(11):758-772.

[8] Hamrick J M, Wm B Mills. Analysis of temperatures in connoting pond as influenced by the peach bottom atomic power plant thermal discharge[J].Environmental Science and Policy,2001(3):197-209.

[9] 任华堂,于 良,夏建新,等. 黄河内蒙古段水污染事故应急预警模型研究[J].应用基础与工程科学学报，2012(9).67-75.

[10] WU G, XU Z. Prediction of algal blooming using EFDC model: Case study in the Daoxiang Lake [J]. Ecol Model, 2011,222(6):1 245-52.

[11] WANG Y, JIANG Y, LIAO W, et al. 3-D hydro-environmental simulation of Miyun reservoir, Beijing[J]. Journal of Hydro-environment Research, 2014,8(4):383-95.

[12] 王宇晖. 基于分布式水文模型的流域水循环及面源伴生过程模拟研究与应用[D]. 上海：东华大学，2012.

[13] 李 兴. 内蒙古乌梁素海水质动态数值模拟研究[D]. 呼和浩特：内蒙古农业大学，2009.

[14] 李 杰. Falls Lake水库水质的数值模拟研究及分析[D]. 山东青岛：中国海洋大学，2010.

[15] 李一平，唐春燕，余钟波,等. 大型浅水湖泊水动力模型不确定性和敏感性分析[J]. 水科学进展，2012,23(2):271-277.